Inversión (geometría)

guardan una relación de inversión con respecto a la circunferencia

, cuando se cumple que: También puede explicarse como, dados un punto fijo O de un plano un número real k distinto de cero, se entiende por inversión de centro el punto O y potencia k a la transformación geométrica que a cada punto P del plano se le hace corresponder otro P' del mismo, alineado con P tal que se cumple que OPxOP'=k.

respecto a una circunferencia dada se determina de la forma siguiente: En coordenadas cartesianas: En coordenadas polares: Esta última forma justifica el término inversión utilizado para denominar a esta relación entre puntos con respecto a una circunferencia de radio 1.

En el plano complejo se define la aplicación de inversión generalizada con respecto a un círculo unitario.

En términos de números complejos, la transformación se caracteriza por la aplicación siguiente:[2]​ siendo

es el origen en un sistema de coordenadas cartesiano tridimensional, entonces se puede determinar la inversión en la esfera

Otras dos circunferencias con centro en los dos puntos anteriores y que pasen por

pertenece a la circunferencia de inversión, entonces no es necesaria ninguna construcción, dado que

En función de si el punto A se encuentra dentro o fuera de la circunferencia, se tienen dos construcciones distintas, que se muestran en la figura de la derecha: Debe notarse que si el punto A coincide con el centro o de la circunferencia (c), entonces los puntos 2 y 4 (del caso 1) se disponen en una recta paralela a la recta D-E, lo que implica que el punto A' es el punto del infinito.

Son similares a los casos de la reflexión ordinaria sobre una línea recta contenida en un plano o sobre un plano contenido en el espacio y tienen, así, las siguientes propiedades: Sin embargo, presentan diferencias significativas: Las inversiones siempre han jugado un papel importante en la geometría.

Las imágenes inversas de cónicas y cuádricas en el espacio son curvas algebraicas de cuarto grado como máximo, con propiedades interesantes (véanse los ejemplos posteriores).

es una circunferencia a través del origen con la ecuación En los siguientes ejemplos, en lugar de

se asigna a una cardioide mediante la reflexión circular utilizando la ecuación

La inversión de una parábola se puede asociar a sus rectas tangentes, que se transforman en una serie de circunferencias que pasan a través del punto origen.

se transforma mediante su reflexión en el círculo unitario, en una lemniscata con la ecuación

Dado que las circunferencias y las esferas que no pasan a través del origen (el centro de inversión) se transforman de nuevo en elementos del mismo tipo, se pueden generar superficies complejas por inversión a partir de superficies simples que contienen muchas circunferencias.

La superficie más simple para visualizar una inversión es una esfera con circunferencias de longitud y latitud.

Si la esfera de la que se está creando la imagen tiene la ecuación

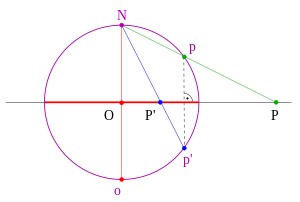
Dado que las líneas rectas del plano se representan en círculos a través del Polo Norte, la red produce dos grupos de dichos círculos, cada uno con la misma tangente en el Polo Norte.

Dado que una inversión y, por lo tanto, también una proyección estereográfica comserva los ángulos (véase más abajo), las circunferencias se tocan entre sí (en N) o se intersecan verticalmente en N y en otro punto.

Análogamente al caso bidimensional, la noción de inversión puede transferirse a un espacio euclidiano n-dimensional y estudiarse analíticamente: Al igual que con la prueba de que una reflexión circular convierte líneas rectas y circunferencias se transforman en elementos de estos tipos, se demuestra con la ayuda del cálculo vectorial que, en el caso general: Sea

Entonces se aplica De manera similar, para otra curva regular

La geometría proyectiva está ligada al concepto geométrico de inversión, y valiéndose de sus propiedades pueden resolver determinados problemas:[5]​ Sea C una circunferencia con centro en O y radio r y sea A un punto diferente de O.

Al punto O se le llama centro de inversión.

Se dice que los puntos A y B son inversamente simétricos el uno del otro.

Sea r una recta que no pase por el centro de inversión O y sea P el pie de la perpendicular a r por el punto O y Q su imagen en la inversión.

B es vértice del ángulo recto de un triángulo rectángulo cuyos lados pasan por los puntos O y Q.

En esta inversión, los puntos D y E son uno imagen del otro.

De manera semejante, se puede demostrar que los puntos C y F son inversamente simétricos en la mencionada inversión.

Puesto que la secante r es arbitaria se concluye que Por otra parte, los puntos A, B, D y E son concíclicos, esto es se hallan sobre una circunferencia.