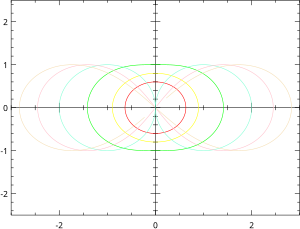
Hipopoda
En geometría, una hipopoda (del griego antiguo ἱπποπέδη, vínculo para inmovilizar las patas de un caballo) es un curva plana determinada por una ecuación de la forma donde se supone que c > 0 y que c > d, ya que los casos restantes se reducen a un solo punto o se pueden expresar en la forma dada mediante una rotación.
Las hipopodas son curvas algebraicas racionales bicirculares de grado 4, simétricas con respecto a los ejes x e y.
Las hipopodas se pueden definir como la curva formada por la intersección de un toro y un plano, donde el plano es paralelo al eje del toro y tangente a él en el círculo interior.
Por lo tanto, es un spira de Perseo que a su vez es un tipo de sección tórica.
Si se gira un círculo con radio a alrededor de un eje a la distancia b desde su centro, entonces la ecuación de la hipopoda resultante en coordenadas polares es o en coordenadas cartesianas Debe tenerse en cuenta que cuando a > b, el toro se interseca a sí mismo, por lo que no se parece a la imagen habitual de un toro.