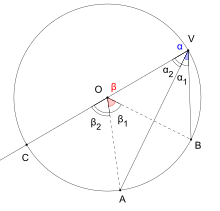
Ángulo inscrito
En geometría, un ángulo inscrito está formado por dos cuerdas y su vértice está sobre la circunferencia.
Su valor es la mitad del ángulo central correspondiente.
Mientras que un ángulo central tiene una amplitud
igual a la del arco que abarca, la del ángulo inscrito es la mitad de la porción de circunferencia en su interior,
Entre otros resultados, esta propiedad permite demostrar que los ángulos opuestos de un cuadrilátero cíclico son suplementarios, y que cuando dos cuerdas
se intersecan en el interior del círculo, el producto de la longitud de sus segmentos es el mismo
Para demostrar que la propiedad descrita antes es cierta siempre, demostraremos por separado que lo es cuando una cuerda es el diámetro, cuando el centro del círculo está en el interior del ángulo y cuando el centro del círculo está en el exterior del ángulo.
De esta manera quedará demostrado para cualquier caso.
el otro extremo de la cuerda que pasa por
es la amplitud del arco comprendido entre las secantes
tiene dos lados con longitud igual al radio (
Dado que la suma de los ángulos internos de un triángulo es 180°, tenemos que
y lo alargamos hasta que interseque la circunferencia en el punto
Supongamos que el centro de la circunferencia
es el punto diamentralmente opuesto a
también son ángulos inscritos, pero cada uno de estos ángulos tiene un lado que pasa por el centro y, por lo tanto, podemos aplicar la conclusión del apartado anterior a ambos.
Entre estos tres ángulos tenemos la relación
(2) Por la demostración cuando una cuerda es el diámetro tenemos que
Combinando estos resultados con la ecuación (2) tenemos que
Y, por la ecuación (1), obtenemos que
y lo alargamos hasta que interseque la circunferencia en el punto
Supongamos que el centro de la circunferencia
está fuera del ángulo
no incluye el punto
es el punto diamentralmente opuesto a
también son ángulos inscritos, pero cada uno de estos ángulos tiene un lado que pasa por el centro y, por lo tanto, podemos aplicar la conclusión del primer apartado a ambos.
Entre estos tres ángulos tenemos la relación
(4) Por la demostración cuando una cuerda es el diámetro tenemos que
Combinando estos resultados con la ecuación (4) tenemos que
Y, por la ecuación (3), obtenemos que