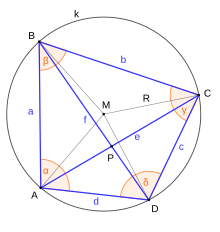
Cuadrilátero cíclico

Las fórmulas y propiedades dadas a continuación son válidas para el caso convexo.La palabra cíclico tiene su origen en el griego antiguo κύκλος (kuklos) que significa "círculo" o "rueda".[7]​[8]​[3]​ Si dos líneas rectas, una que contiene el segmento AC y la otra que contiene el segmento BD, se cruzan en P, entonces los cuatro puntos A, B, C, D son concíclicos si y solo si[9]​ La intersección P puede ser interna o externa al círculo.Otra caracterización más es que un cuadrilátero convexo ABCD es cíclico si y solo si[10]​ El área K de un cuadrilátero cíclico con lados a, b, c y d viene dada por la fórmula de Brahmagupta[6]​: p.24 donde s es el semiperímetro del cuadrilátero (s = 1/2(a + b + c + d)).Siempre que A no sea un ángulo recto, el área también se puede expresar como[6]​: p.26 Otra fórmula es[13]​: p.83 donde R es el radio de la circunferencia circunscrita.En un cuadrilátero cíclico con vértices sucesivos A, B, C y D; y lados a = AB, b = BC, c = CD y d = DA, las longitudes de las diagonales p = AC y q = BD se pueden expresar en términos de los lados como[6]​ : p.25,  [15]​[16]​ : p. 84 mostrando el Teorema de Ptolomeo Según el "segundo teorema de Ptolomeo",[6]​: p.25,  [15]​ usando la misma notación que arriba.Cualquiera de estos dos cuadriláteros cíclicos tienen una longitud diagonal en común.[16]​: p.[6]​: p.31 Un cuadrilátero cíclico con lados sucesivos a, b, c y d; y con semiperímetro s; tiene el circunradio (el radio del circuncírculo) dado por[15]​[21]​ Esta fórmula fue deducida por el matemático indio Vatasseri Paramésuara en el siglo XV.Así, en un cuadrilátero cíclico, el circuncentro, el "centroide de vértices" y el anticentro son colineales.[23]​ Si las diagonales de un cuadrilátero cíclico se cruzan en P, y los puntos medios de las diagonales son M y N, entonces el anticentro del cuadrilátero es el ortocentro del triángulo MNP.Esto se cumple porque las diagonales son cuerdas de la circunferencia perpendiculares entre sí.El resultado es[28]​: p.222 En geometría esférica, un cuadrilátero esférico formado a partir de cuatro círculos máximos que se cruzan es cíclico si y solo si las sumas de los ángulos opuestos son iguales, es decir, α + γ = β + δ para ángulos consecutivos α, β, γ y δ del cuadrilátero.A. Lexell comprobó en 1786 este teorema en un sentido[30]​ demostrando que en un cuadrilátero esférico inscrito en una circunferencia no máxima de una esfera, las sumas de ángulos opuestos son iguales, y que en el cuadrilátero circunscrito las sumas de lados opuestos son iguales.