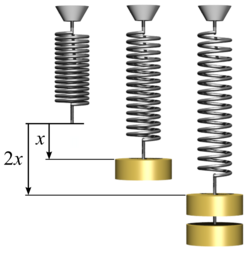
Ley de elasticidad de Hooke
En física, la ley de elasticidad de Hooke o ley de Hooke[1] establece que el alargamiento unitario que experimenta un cuerpo elástico es directamente proporcional a la fuerza aplicada sobre el mismo (
Esta ley comprende numerosas disciplinas, siendo utilizada en ingeniería y construcción, así como en la ciencia de los materiales.
Finalmente debe fallar una vez que las fuerzas excedan algún límite, ya que ningún material puede comprimirse más allá de un cierto tamaño mínimo, o estirarse más allá de un tamaño máximo, sin alguna deformación permanente o cambio de estado.
La ley de Hooke es una aproximación precisa para la mayoría de los cuerpos sólidos, siempre que las fuerzas y deformaciones sean lo suficientemente pequeñas.
Esta ley recibe su nombre del físico inglés Robert Hooke, contemporáneo de Isaac Newton, y contribuyente prolífico de la arquitectura.
El anagrama significa Ut tensio sic vis ("como la extensión, así la fuerza").
[cita requerida] La forma más común de representar matemáticamente la Ley de Hooke es mediante la ecuación del muelle o resorte, donde se relaciona la fuerza (
) provocado por la fuerza externa aplicada al extremo del mismo:
) se llama constante elástica del resorte y (
) asociada al estiramiento del resorte viene dada por la siguiente ecuación:
Teniendo en cuenta esta Ley de Hooke del muelle y además, la masa del objeto que oscila, y su aceleración, se obtiene como solución el movimiento del oscilador armónico simple (Véase también: Muelle elástico / Resorte).
Esto se debe a que una onda tiene la doble dependencia espacial y temporal a la vez (Véase también: Muelle elástico / Resorte).
En la mecánica de sólidos deformables elásticos la distribución de tensiones es mucho más complicada que en un resorte o una barra estirada solo según su eje.
La deformación en el caso más general necesita ser descrita mediante un tensor de deformaciones mientras que los esfuerzos internos en el material necesitan ser representados por un tensor de tensiones.
En este caso, los materiales dúctiles que poseen un punto de cedencia definido; en ciertos materiales no puede definirse la proporcionalidad de cedencia fácilmente, ya que es difícil determinar con precisión el valor del esfuerzo (
Al utilizar la ley de Hooke en valores mayores que el límite de proporcionalidad no conducirá a ningún error significativo.
En el caso de un problema unidimensional donde las deformaciones o tensiones en direcciones perpendiculares a una dirección dada son irrelevantes o se pueden ignorar (
Por otro lado, las ecuaciones de Lamé-Hooke para un sólido elástico lineal e isótropo pueden ser deducidas del teorema de Rivlin-Ericksen, que pueden escribirse en la forma:
De hecho para un material ortotrópico la relación entre las componentes del tensor tensión y las componentes del tensor deformación viene dada por:
Como puede verse las componentes que gobiernan el alargamiento y las que gobiernan la distorsión están desacopladas, lo cual significa que en general es posible producir alargamientos en torno a un punto sin provocar distorsiones y viceversa.
Las ecuaciones inversas que dan las deformaciones en función de las tensiones toman una forma algo más complicada:
{\displaystyle {\begin{pmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\sigma _{xy}\\\sigma _{xz}\\\sigma _{yz}\end{pmatrix}}={\begin{pmatrix}{\frac {1-\nu _{yz}\nu _{yz}}{E_{y}E_{z}\Delta }}&{\frac {\nu _{yx}+\nu _{yz}\nu _{zx}}{E_{y}E_{z}\Delta }}&{\frac {\nu _{zx}+\nu _{zy}\nu _{yx}}{E_{y}E_{z}\Delta }}&&&\\{\frac {\nu _{xy}+\nu _{xz}\nu _{zy}}{E_{x}E_{z}\Delta }}&{\frac {1-\nu _{zx}\nu _{xz}}{E_{x}E_{z}\Delta }}&{\frac {\nu _{zy}+\nu _{zx}\nu _{xy}}{E_{x}E_{z}\Delta }}&&&\\{\frac {\nu _{xz}+\nu _{xy}\nu _{yz}}{E_{x}E_{y}\Delta }}&{\frac {\nu _{yz}+\nu _{yx}\nu _{xz}}{E_{x}E_{y}\Delta }}&{\frac {1-\nu _{xy}\nu _{yx}}{E_{x}E_{y}\Delta }}\\&&&2G_{xy}&0&0\\&&&0&2G_{xz}&0\\&&&0&0&2G_{yz}\\\end{pmatrix}}{\begin{pmatrix}\varepsilon _{xx}\\\varepsilon _{yy}\\\varepsilon _{zz}\\\varepsilon _{xy}\\\varepsilon _{xz}\\\varepsilon _{yz}\end{pmatrix}}}
Las deformaciones lineales de materiales elásticos se pueden aproximar como procesos adiabáticos .
En estas condiciones y para procesos cuasiestáticos, la primera ley de la termodinámica para un cuerpo deformado se puede expresar como
Usando la relación entre el esfuerzo de Cauchy y la superficie de tracción, t = n · σ (donde n es el vector normal unitario exterior a
Usando la simetría del esfuerzo de Cauchy y la identidad
y por lo tanto la variación en la densidad de energía interna viene dada por
y la variación de la energía interna se puede expresar como
Podemos ver por qué c debe ser un tensor de cuarto rango observando que, para un material elástico lineal, En notación de índice La constante del lado derecho requiere cuatro índices y es una cantidad de cuarto rango.
También podemos demostrar que la constante obedece a las reglas de transformación del tensor para tensores de cuarto rango.