Puntos concíclicos

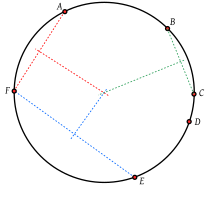
En geometría , se dice que un conjunto de puntos es concíclico (o cocíclico ) si se encuentran en un círculo común . Un polígono cuyos vértices son concíclicos se llama polígono cíclico , y al círculo se le llama círculo circunscrito o circuncírculo . Todos los puntos concíclicos están equidistantes del centro del círculo.

Tres puntos en el plano que no caen todos en línea recta son concíclicos, por lo que cada triángulo es un polígono cíclico, con una circunferencia circunscrita bien definida . Sin embargo, cuatro o más puntos del plano no son necesariamente concíclicos. Después de los triángulos, el caso especial de los cuadriláteros cíclicos ha sido el más estudiado.

Bisectrices perpendiculares

En general, el centro O de un círculo en el que se encuentran los puntos P y Q debe ser tal que OP y OQ estén a distancias iguales. Por lo tanto O debe estar en la mediatriz del segmento de recta PQ . ^[1] Para n puntos distintos hay n ( n − 1)/2 bisectrices, y la condición concíclica es que todas se encuentran en un solo punto, el centro O .

triangulos

Los vértices de cada triángulo caen sobre un círculo llamado círculo circunstante . (Debido a esto, algunos autores definen "concíclico" sólo en el contexto de cuatro o más puntos en un círculo). ^[2] Varios otros conjuntos de puntos definidos a partir de un triángulo también son concíclicos, con círculos diferentes; véase Círculo de nueve puntos ^[3] y Teorema de Lester . ^[4]

El radio del círculo en el que se encuentran un conjunto de puntos es, por definición, el radio del círculo circunstante de cualquier triángulo con vértices en tres de esos puntos. Si las distancias por pares entre tres de los puntos son a , b y c , entonces el radio del círculo es

R={\sqrt {\frac {a^{2}b^{2}c^{2}}{(a+b+c)(-a+b+c)(a-b+c )(a+bc)}}}.

Aquí se dan la ecuación de la circunferencia circunscrita de un triángulo y las expresiones para el radio y las coordenadas del centro del círculo, en términos de las coordenadas cartesianas de los vértices .

Otros puntos concíclicos

En cualquier triángulo todos los nueve puntos siguientes son concíclicos en lo que se llama círculo de nueve puntos : los puntos medios de las tres aristas, los pies de las tres altitudes y los puntos intermedios entre el ortocentro y cada uno de los tres vértices.

El teorema de Lester establece que en cualquier triángulo escaleno , los dos puntos de Fermat , el centro de nueve puntos y el circuncentro son concíclicos.

Si por el punto de Lemoine se trazan rectas paralelas a los lados de un triángulo, entonces los seis puntos de intersección de las rectas y los lados del triángulo son concíclicos, en lo que se denomina círculo de Lemoine .

El círculo de van Lamoen asociado a cualquier triángulo dado contiene los circuncentros de los seis triángulos que están definidos en su interior por sus tres medianas . $T$ $T$

El circuncentro de un triángulo , su punto de Lemoine y sus dos primeros puntos de Brocard son concíclicos, siendo el segmento desde el circuncentro hasta el punto de Lemoine un diámetro . ^[5]

Cuadriláteros cíclicos

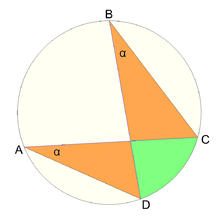
Un cuadrilátero ABCD con vértices concíclicos se llama cuadrilátero cíclico ; esto sucede si y solo si (el teorema del ángulo inscrito ), lo cual es cierto si y solo si los ángulos opuestos dentro del cuadrilátero son suplementarios . ^[6] Un cuadrilátero cíclico con lados sucesivos a , b , c , d y semiperímetro s = ( a + b + c + d ) / 2 tiene su circunradio dado por ^[7]^[8] $\angle CAD=\angle CBD$

R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ac+bd)(ad+bc)}{(sa)(sb)(sc)(sd) )}}},

una expresión que fue derivada por el matemático indio Vatasseri Parameshvara en el siglo XV.

Según el teorema de Ptolomeo , si un cuadrilátero está dado por las distancias por pares entre sus cuatro vértices A , B , C y D en orden, entonces es cíclico si y sólo si el producto de las diagonales es igual a la suma de los productos de los lados opuestos. :

AC\cdot BD=AB\cdot CD+BC\cdot AD.

Si dos líneas, una que contiene el segmento AC y la otra que contiene el segmento BD , se cruzan en X , entonces los cuatro puntos A , B , C , D son concíclicos si y solo si ^[9]

\displaystyle AX\cdot XC=BX\cdot XD.

La intersección X puede ser interna o externa al círculo. Este teorema se conoce como potencia de un punto .

Un cuadrilátero convexo es ortodiagonal (tiene diagonales perpendiculares) si y sólo si los puntos medios de los lados y los pies de las cuatro alturas son ocho puntos concíclicos, sobre lo que se llama círculo de ocho puntos .

polígonos cíclicos

De manera más general, un polígono en el que todos los vértices son concíclicos se denomina polígono cíclico . Un polígono es cíclico si y sólo si las bisectrices perpendiculares de sus aristas son concurrentes . ^[10] Todo polígono regular es un polígono cíclico.

Para un polígono cíclico con un número impar de lados, todos los ángulos son iguales si y sólo si el polígono es regular. Un polígono cíclico con un número par de lados tiene todos los ángulos iguales si y solo si los lados alternos son iguales (es decir, los lados 1, 3, 5,… son iguales y los lados 2, 4, 6,… son iguales). ^[11]

Un pentágono cíclico con lados y área racionales se conoce como pentágono de Robbins . En todos los casos conocidos, sus diagonales también tienen longitudes racionales, aunque es un problema sin resolver si esto es cierto para todos los pentágonos de Robbins posibles. ^[12]

En cualquier $n$ -gón cíclico con $n$ par , la suma de un conjunto de ángulos alternos (el primero, tercero, quinto, etc.) es igual a la suma del otro conjunto de ángulos alternos. Esto se puede demostrar por inducción a partir del caso $n = 4$ , reemplazando en cada caso un lado por tres lados más y observando que estos tres lados nuevos junto con el lado antiguo forman un cuadrilátero que a su vez tiene esta propiedad; los ángulos alternos del último cuadrilátero representan las sumas a las sumas de los ángulos alternos del $n$ -gon anterior.

Un polígono tangencial es aquel que tiene un círculo inscrito tangente a cada lado del polígono; estos puntos de tangencia son, por tanto, concíclicos en el círculo inscrito. Sea un $n$ -gón inscrito en un círculo y otro $n$ -gón sea tangencial a ese círculo en los vértices del primer $n$ -gón. Entonces, desde cualquier punto $P$ del círculo, el producto de las distancias perpendiculares desde $P$ a los lados del primer $n$ -gón es igual al producto de las distancias perpendiculares desde $P$ a los lados del segundo $n$ -gón. ^[13]

Punto en el círculo circunstante

$Sea un n$ -gon cíclico $que$ tenga vértices $A 1,\dots, An$ en el círculo unitario. Entonces $,$ para cualquier punto $M$ en el arco menor $A 1 An$ , las distancias desde $M$ a los vértices satisfacen ^[14]

{\begin{casos}{\overline {MA_{1}}}+{\overline {MA_{3}}}+\cdots +{\overline {MA_{n-2}}}+{\overline {MA_{n}}}<n/{\sqrt {2}}&{\text{si }}n{\text{ es impar}};\\{\overline {MA_{1}}}+{\ overline {MA_{3}}}+\cdots +{\overline {MA_{n-3}}}+{\overline {MA_{n-1}}}\leq n/{\sqrt {2}}&{ \text{si }}n{\text{ es par}}.\end{cases}}

$Para un n$ -gon regular , si son las distancias desde cualquier punto $M$ de la circunferencia hasta los vértices $Ai$ $,$ entonces ^[15] ${\overline {MA_{i}}}$

3({\overline {MA_{1}}}^{2}+{\overline {MA_{2}}}^{2}+\dots +{\overline {MA_{n}}}^{ 2})^{2}=2n({\overline {MA_{1}}}^{4}+{\overline {MA_{2}}}^{4}+\dots +{\overline {MA_{n) }}}^{4}).

Constante circunscrita del polígono

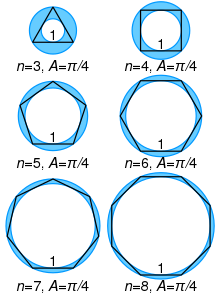
Cualquier polígono regular es cíclico. Considere un círculo unitario, luego circunscriba un triángulo regular de modo que cada lado toque el círculo. Circunscribe un círculo y luego circunscribe un cuadrado. De nuevo circunscribe un círculo, luego circunscribe un pentágono regular , y así sucesivamente. Los radios de los círculos circunscritos convergen a la llamada constante circunscrita del polígono.

\prod _{n=3}^{\infty }{\frac {1}{\cos \left({\frac {\pi }{n}}\right)}}=8.7000366\ldots .

(secuencia A051762 en la OEIS ). El recíproco de esta constante es la constante de Kepler-Bouwkamp .

Variaciones

En contextos donde se considera que las líneas son un tipo de círculo generalizado con radio infinito, los puntos colineales (puntos a lo largo de una sola línea) se consideran concíclicos. Este punto de vista es útil, por ejemplo, cuando se estudia la inversión a través de un círculo o, más generalmente, las transformaciones de Möbius (transformaciones geométricas generadas por reflexiones e inversiones de círculos), ya que estas transformaciones preservan la conciclicidad de los puntos sólo en este sentido extendido. ^[dieciséis]

En el plano complejo (formado al ver las partes real e imaginaria de un número complejo como las coordenadas cartesianas x e y del plano), la conciclicidad tiene una formulación particularmente simple: cuatro puntos en el plano complejo son concíclicos o colineales si y solo si su razón cruzada es un número real . ^[17]

Área entera y longitudes de lados

Algunos polígonos cíclicos tienen la propiedad de que su área y la longitud de todos sus lados son números enteros positivos. Los triángulos con esta propiedad se denominan triángulos heronianos ; los cuadriláteros cíclicos con esta propiedad (y que las diagonales que conectan vértices opuestos tienen longitud entera) se llaman cuadriláteros de Brahmagupta ; Los pentágonos cíclicos con esta propiedad se llaman pentágonos de Robbins . De manera más general, las versiones de estos polígonos cíclicos escaladas por un número racional tendrán áreas y longitudes de lados que son números racionales.

Sea $θ 1$ el ángulo que abarca un lado del polígono cíclico visto desde el centro del círculo circunscrito. De manera similar, defina los ángulos centrales $θ 2, ..., θ n$ $para los n - 1$ lados restantes . Cada triángulo heroniano y cada cuadrilátero de Brahmagupta tiene un valor racional para la tangente del cuarto de ángulo, $tan θ k /4$ , para cada valor de $k$ . Todo pentágono de Robbins conocido (tiene diagonales que tienen longitud racional y) tiene esta propiedad, aunque es un problema no resuelto si todos los pentágonos de Robbins posibles tienen esta propiedad.

Lo contrario es cierto para todos los polígonos cíclicos con cualquier número de lados; Si todos esos ángulos centrales tienen tangentes racionales para sus cuartos de ángulo, entonces el polígono cíclico implícito circunscrito por el círculo unitario tendrá simultáneamente longitudes de lados racionales y área racional. Además, cada diagonal que conecta dos vértices, sean o no adyacentes, tendrá una longitud racional. Un polígono cíclico de este tipo se puede escalar de modo que su área y longitud sean todas enteras.

Esta relación inversa proporciona una forma de generar polígonos cíclicos con área, lados y diagonales enteros. Para un polígono con $n$ lados, sean $0 < c 1 < ... < c n -1 < +\infty$ números racionales. Estas son las tangentes de un cuarto de los ángulos acumulativos $θ 1$ , $θ 1 + θ 2$ , ..., $θ 1 + ... + θ n -1$ . Sea $q 1 = c 1$ , sea $q n = 1 / c n -1$ , y sea $q k = (c k - c k -1) / (1 + c k c k -1)$ para $k = 2, .. ., norte -1$ . Estos números racionales son las tangentes de los cuartos de ángulo individuales, usando la fórmula para la tangente de la diferencia de ángulos. Las longitudes de los lados racionales del polígono circunscrito por el círculo unitario se obtienen así como $s k = 4 q k / (1 + q k 2)$ . El área racional es $A = \sum k 2 q k (1 - q k 2) / (1 + q k 2) 2$ . Estos se pueden convertir en números enteros escalando las longitudes de los lados mediante una constante compartida.

Otras propiedades

Un conjunto de cinco o más puntos es concíclico si y sólo si cada subconjunto de cuatro puntos es concíclico. ^[18] Esta propiedad puede considerarse como un análogo de la conciclicidad de la propiedad de Helly de los conjuntos convexos.

Círculo delimitador mínimo

Una noción relacionada es la de círculo delimitador mínimo , que es el círculo más pequeño que contiene completamente un conjunto de puntos. Cada conjunto de puntos en el plano tiene un círculo delimitador mínimo único, que puede construirse mediante un algoritmo de tiempo lineal . ^[19]

Incluso si un conjunto de puntos es concíclico, su círculo circunscrito puede ser diferente de su círculo delimitador mínimo. Por ejemplo, para un triángulo obtuso , el círculo delimitador mínimo tiene el lado más largo como diámetro y no pasa por el vértice opuesto.

Referencias

^ Libeskind, Shlomo (2008), Geometría euclidiana y transformacional: una investigación deductiva, Jones & Bartlett Learning, p. 21, ISBN 9780763743666/
^ Elliott, John (1902), Geometría elemental, Swan Sonnenschein & co., p. 126.
^ Isaacs, I. Martin (2009), Geometría para estudiantes universitarios, textos universitarios puros y aplicados, vol. 8, Sociedad Matemática Estadounidense, pág. 63, ISBN 9780821847947.
^ Yiu, Paul (2010), "Los círculos de Lester, Evans, Parry y sus generalizaciones" (PDF) , Forum Geometriorum , 10 : 175–209, MR 2868943.
^ Scott, JA "Algunos ejemplos del uso de coordenadas de área en geometría de triángulos", Mathematical Gazette 83, noviembre de 1999, 472–477.
^ Pedoe, Dan (1997), Círculos: una visión matemática, MAA Spectrum (2ª ed.), Cambridge University Press, p. XXII, ISBN 9780883855188.
^ Alsina, Claudi; Nelsen, Roger B. (2007), "Sobre las diagonales de un cuadrilátero cíclico" (PDF) , Forum Geometriorum , 7 : 147–9
^ Hoehn, Larry (marzo de 2000), "Circumradio de un cuadrilátero cíclico", Mathematical Gazette , 84 (499): 69–70, doi :10.2307/3621477, JSTOR 3621477
^ Bradley, Christopher J. (2007), El álgebra de la geometría: coordenadas cartesianas, regionales y proyectivas , Highperception, p. 179, ISBN 978-1906338008, OCLC 213434422
^ Byer, Owen; Lazebnik, Félix; Smeltzer, Deirdre L. (2010), Métodos de geometría euclidiana, Asociación Matemática de América, p. 77, ISBN 9780883857632.
^ De Villiers, Michael (marzo de 2011). "95.14 Polígonos circunscritos equiláteros y cíclicos equiangulares". La Gaceta Matemática . 95 (532): 102-107. doi :10.1017/S0025557200002461. JSTOR 23248632. S2CID 233361080.
^ Buchholz, Ralph H.; MacDougall, James A. (2008). "Polígonos cíclicos de lados y área racionales". Revista de teoría de números . 128 (1): 17–48. doi : 10.1016/j.jnt.2007.05.005 . SEÑOR 2382768.
^ Johnson, Roger A. (1929). Geometría moderna: un tratado elemental sobre la geometría del triángulo y el círculo . Houghton Mifflin Co. pág. 72. hdl :2027/wu.89043163211.Republicado por Dover Publications como Geometría euclidiana avanzada , 1960 y 2007.
↑ «Desigualdades propuestas en Crux Mathematicorum» (PDF) . El Compendio de la OMI . pag. 190, #332.10.
^ Meskhishvili, Mamuka (2020). "Promedios cíclicos de polígonos regulares y sólidos platónicos". Comunicaciones en Matemáticas y Aplicaciones . 11 : 335–355. arXiv : 2010.12340 . doi :10.26713/cma.v11i3.1420 (inactivo el 31 de enero de 2024).{{cite journal}}: Mantenimiento CS1: DOI inactivo a partir de enero de 2024 ( enlace )
^ Zwikker, C. (2005), La geometría avanzada de las curvas planas y sus aplicaciones, Publicaciones Courier Dover, p. 24, ISBN 9780486442761.
^ Hahn, Liang-shin (1996), Geometría y números complejos, MAA Spectrum (2ª ed.), Cambridge University Press, p. 65, ISBN 9780883855102.
^ Pedoe, Dan (1988), Geometría: un curso completo, Publicaciones Courier Dover, pág. 431, ISBN 9780486658124.
^ Meguido, N. (1983). "Algoritmos de tiempo lineal para programación lineal en R ³ y problemas relacionados". Revista SIAM de Computación . 12 (4): 759–776. doi :10.1137/0212052. S2CID 14467740.

enlaces externos

Weisstein, Eric W. "Concíclico". MundoMatemático .
Cuatro puntos concíclicos de Michael Schreiber, The Wolfram Demonstrations Project .

Wikimedia Commons tiene medios relacionados con los puntos concíclicos .