El bosón de Higgs , a veces llamado partícula de Higgs , [9] [10] es una partícula elemental en el Modelo Estándar de física de partículas producida por la excitación cuántica del campo de Higgs , [11] [12] uno de los campos en la teoría de la física de partículas . [12] En el Modelo Estándar, la partícula de Higgs es un bosón escalar masivo con espín cero, paridad par (positiva) , sin carga eléctrica y sin carga de color que se acopla a (interactúa con) la masa. [13] También es muy inestable y se desintegra en otras partículas casi inmediatamente después de su generación.
El campo de Higgs es un campo escalar con dos componentes neutros y dos eléctricamente cargados que forman un doblete complejo de la simetría isospín débil SU(2). Su " potencial de Sombrero " lo lleva a tomar un valor distinto de cero en todas partes (incluso en el espacio vacío), lo que rompe la simetría isospín débil de la interacción electrodébil y, a través del mecanismo de Higgs , da una masa en reposo a todas las partículas elementales masivas del Modelo Estándar, incluido el propio bosón de Higgs. La existencia del campo de Higgs se convirtió en la última parte no verificada del Modelo Estándar de la física de partículas, y durante varias décadas se consideró "el problema central de la física de partículas". [14] [15]
Tanto el campo como el bosón reciben su nombre del físico Peter Higgs , quien en 1964, junto con otros cinco científicos en tres equipos, propuso el mecanismo de Higgs , una forma en que algunas partículas adquirían masa . Todas las partículas fundamentales conocidas en ese momento [c] deberían carecer de masa a energías muy altas, pero explicar por completo cómo algunas partículas ganan masa a energías más bajas había sido extremadamente difícil. Si estas ideas eran correctas, también debería existir una partícula conocida como bosón escalar (con ciertas propiedades). Esta partícula se llamó bosón de Higgs y podría usarse para probar si el campo de Higgs era la explicación correcta.
Después de una búsqueda de 40 años , en 2012 los experimentos ATLAS y CMS del Gran Colisionador de Hadrones (LHC) del CERN , cerca de Ginebra (Suiza), descubrieron una partícula subatómica con las propiedades esperadas. Posteriormente se confirmó que la nueva partícula coincidía con las propiedades esperadas de un bosón de Higgs. Los físicos de dos de los tres equipos, Peter Higgs y François Englert , recibieron el Premio Nobel de Física en 2013 por sus predicciones teóricas. Aunque el nombre de Higgs se ha asociado con esta teoría, varios investigadores entre 1960 y 1972 desarrollaron de forma independiente diferentes partes de ella.
En los medios de comunicación, el bosón de Higgs ha sido llamado a menudo la " partícula de Dios " en honor al libro La partícula de Dios de 1993 del Premio Nobel Leon Lederman . [16] El nombre ha sido criticado por los físicos, [17] [18] incluido Peter Higgs . [19]
Los físicos explican las partículas y fuerzas fundamentales de nuestro universo en términos del Modelo Estándar , un marco ampliamente aceptado basado en la teoría cuántica de campos que predice casi todas las partículas y fuerzas conocidas aparte de la gravedad con gran precisión. (Se utiliza una teoría separada, la relatividad general , para la gravedad). En el Modelo Estándar, las partículas y fuerzas en la naturaleza (aparte de la gravedad) surgen de propiedades de campos cuánticos conocidos como invariancia de calibre y simetrías . Las fuerzas en el Modelo Estándar son transmitidas por partículas conocidas como bosones de calibre . [20] [21]
Las teorías de invariancia de calibre son teorías que tienen una característica útil, a saber: algunos tipos de cambios en el valor de ciertos elementos no hacen ninguna diferencia en los resultados o las mediciones que hacemos. Por ejemplo: cambiar los voltajes en un electroimán en +100 voltios no causa ningún cambio en el campo magnético que produce. De manera similar, medir la velocidad de la luz en el vacío parece dar el mismo resultado, independientemente de la ubicación en el tiempo y el espacio, y cualquiera que sea el campo gravitatorio local .
En este tipo de teorías, el calibre es un elemento cuyo valor podemos cambiar. El hecho de que algunos cambios dejen inalterados los resultados que medimos significa que se trata de una teoría invariante de calibre, y las simetrías son los tipos específicos de cambios en el calibre que tienen el efecto de dejar inalteradas las mediciones. Las simetrías de este tipo son herramientas poderosas para una comprensión profunda de las fuerzas y partículas fundamentales de nuestro mundo físico. La invariancia de calibre es, por lo tanto, una propiedad importante dentro de la teoría de la física de partículas. Están estrechamente relacionadas con las leyes de conservación y se describen matemáticamente utilizando la teoría de grupos . La teoría cuántica de campos y el modelo estándar son teorías invariantes de calibre, lo que significa que se centran en las propiedades de nuestro universo, demostrando esta propiedad de invariancia de calibre y las simetrías involucradas.
Las teorías cuánticas de campos basadas en la invariancia de gauge se habían utilizado con gran éxito para comprender las fuerzas electromagnética y fuerte , pero alrededor de 1960, todos los intentos de crear una teoría invariante de gauge para la fuerza débil (y su combinación con la fuerza electromagnética, conocidas en conjunto como interacción electrodébil ) habían fracasado sistemáticamente. Como resultado de estos fracasos, las teorías de gauge comenzaron a caer en descrédito. El problema era que los requisitos de simetría para estas dos fuerzas predecían incorrectamente que los bosones de gauge de la fuerza débil ( W y Z ) tendrían "masa cero" (en la terminología especializada de la física de partículas, "masa" se refiere específicamente a la masa en reposo de una partícula ). Pero los experimentos mostraron que los bosones de gauge W y Z tenían una masa distinta de cero (en reposo). [23]
Además, muchas soluciones prometedoras parecían requerir la existencia de partículas adicionales conocidas como bosones de Goldstone . Pero la evidencia sugería que tampoco existían. Esto significaba que la invariancia de gauge era un enfoque incorrecto o que algo desconocido estaba dando a los bosones W y Z de la fuerza débil su masa, y lo estaba haciendo de una manera que no creaba bosones de Goldstone. A fines de la década de 1950 y principios de la de 1960, los físicos no sabían cómo resolver estos problemas o cómo crear una teoría integral para la física de partículas.
A finales de la década de 1950, Yoichiro Nambu reconoció que la ruptura espontánea de la simetría , un proceso en el que un sistema simétrico se vuelve asimétrico, podría ocurrir bajo ciertas condiciones. [d] La ruptura de la simetría es cuando alguna variable que anteriormente no afectaba los resultados medidos ( originalmente era una "simetría" ) ahora afecta los resultados medidos ( ahora está "rota" y ya no es una simetría ). En 1962, el físico Philip Anderson , un experto en física de la materia condensada , observó que la ruptura de la simetría desempeñaba un papel en la superconductividad y sugirió que también podría ser parte de la respuesta al problema de la invariancia de calibre en la física de partículas.
En concreto, Anderson sugirió que los bosones de Goldstone que resultarían de la ruptura de la simetría podrían, en cambio, en algunas circunstancias, ser "absorbidos" [e] por los bosones W y Z sin masa . Si fuera así, tal vez los bosones de Goldstone no existirían, y los bosones W y Z podrían ganar masa , resolviendo ambos problemas a la vez. Un comportamiento similar ya se había teorizado en superconductividad. [24] En 1964, los físicos Abraham Klein y Benjamin Lee demostraron que esto era teóricamente posible , al menos para algunos casos limitados ( no relativistas ). [25]
Tras los artículos de 1963 [26] y principios de 1964 [25] , tres grupos de investigadores desarrollaron estas teorías de forma independiente de forma más completa, en lo que se conoció como los artículos de ruptura de simetría de PRL de 1964. Los tres grupos llegaron a conclusiones similares y para todos los casos, no solo para algunos casos limitados. Demostraron que las condiciones para la simetría electrodébil se "romperían" si existiera un tipo inusual de campo en todo el universo y, de hecho, no habría bosones de Goldstone y algunos bosones existentes adquirirían masa .
El campo necesario para que esto sucediera (que era puramente hipotético en ese momento) se conoció como el campo de Higgs (en honor a Peter Higgs , uno de los investigadores) y el mecanismo por el cual condujo a la ruptura de la simetría se conoció como el mecanismo de Higgs . Una característica clave del campo necesario es que se necesitaría menos energía para que el campo tuviera un valor distinto de cero que un valor cero, a diferencia de todos los demás campos conocidos, por lo tanto, el campo de Higgs tiene un valor distinto de cero (o expectativa de vacío ) en todas partes . Este valor distinto de cero podría en teoría romper la simetría electrodébil. Fue la primera propuesta capaz de mostrar cómo los bosones de gauge de fuerza débil podían tener masa a pesar de su simetría gobernante, dentro de una teoría invariante de gauge.
Aunque estas ideas no obtuvieron mucho apoyo o atención inicialmente, en 1972 se habían desarrollado hasta convertirse en una teoría integral y demostraron ser capaces de dar resultados "sensatos" que describían con precisión las partículas conocidas en ese momento y que, con una precisión excepcional, predijeron varias otras partículas descubiertas durante los años siguientes . [f] Durante la década de 1970, estas teorías se convirtieron rápidamente en el Modelo Estándar de la física de partículas.
Para permitir la ruptura de la simetría, el Modelo Estándar incluye un campo del tipo necesario para "romper" la simetría electrodébil y dar a las partículas su masa correcta. Se planteó la hipótesis de que este campo, que se conoció como el "Campo de Higgs", existía en todo el espacio y rompía algunas leyes de simetría de la interacción electrodébil , lo que desencadenaba el mecanismo de Higgs. Por lo tanto, causaría que los bosones de calibración W y Z de la fuerza débil fueran masivos a todas las temperaturas por debajo de un valor extremadamente alto. [g] Cuando los bosones de la fuerza débil adquieren masa, esto afecta la distancia que pueden viajar libremente, que se vuelve muy pequeña, lo que también coincide con los hallazgos experimentales. [h] Además, más tarde se comprendió que el mismo campo también explicaría, de una manera diferente, por qué otros componentes fundamentales de la materia (incluidos los electrones y los quarks ) tienen masa.
A diferencia de todos los demás campos conocidos, como el campo electromagnético , el campo de Higgs es un campo escalar y tiene un valor promedio distinto de cero en el vacío .
Todavía no había ninguna evidencia directa de la existencia del campo de Higgs, pero incluso sin una prueba directa, la precisión de sus predicciones llevó a los científicos a creer que la teoría podría ser cierta. En la década de 1980, la cuestión de si el campo de Higgs existía, y por lo tanto si todo el Modelo Estándar era correcto, había llegado a considerarse como una de las preguntas sin respuesta más importantes en la física de partículas . La existencia del campo de Higgs se convirtió en la última parte no verificada del Modelo Estándar de la física de partículas, y durante varias décadas se consideró "el problema central en la física de partículas". [14] [15]
Durante muchas décadas, los científicos no tuvieron forma de determinar si el campo de Higgs existía porque en ese momento no existía la tecnología necesaria para detectarlo. Si el campo de Higgs existiera, sería distinto a cualquier otro campo fundamental conocido, pero también era posible que estas ideas clave, o incluso todo el Modelo Estándar, fueran de alguna manera incorrectas. [i]
La hipótesis de la teoría del bosón de Higgs hizo varias predicciones clave. [f] [28] : 22 Una predicción crucial fue que también debería existir una partícula coincidente , llamada "bosón de Higgs". Probar la existencia del bosón de Higgs probaría si el campo de Higgs existía y, por lo tanto, probaría finalmente si la explicación del Modelo Estándar era correcta. Por lo tanto, hubo una búsqueda exhaustiva del bosón de Higgs , como una forma de probar que el campo de Higgs en sí existía. [11] [12]
Aunque el campo de Higgs existiría en todas partes, probar su existencia no fue nada fácil. En principio, se puede probar su existencia detectando sus excitaciones , que se manifiestan como partículas de Higgs (el bosón de Higgs ), pero estas son extremadamente difíciles de producir y detectar debido a la energía requerida para producirlas y su producción muy rara incluso si la energía es suficiente. Por lo tanto, pasaron varias décadas antes de que se pudiera encontrar la primera evidencia del bosón de Higgs. Los colisionadores de partículas , los detectores y las computadoras capaces de buscar bosones de Higgs tardaron más de 30 años ( c. 1980-2010 ) en desarrollarse. La importancia de esta pregunta fundamental condujo a una búsqueda de 40 años , y a la construcción de una de las instalaciones experimentales más caras y complejas del mundo hasta la fecha, el Gran Colisionador de Hadrones del CERN , [29] en un intento de crear bosones de Higgs y otras partículas para su observación y estudio.
El 4 de julio de 2012 se anunció el descubrimiento de una nueva partícula con una masa entreSe anunció la existencia de 125 y 127 GeV/ c 2 ; los físicos sospecharon que se trataba del bosón de Higgs. [30] [j] [31] [32] Desde entonces, se ha demostrado que la partícula se comporta, interactúa y se desintegra de muchas de las formas predichas para las partículas de Higgs por el Modelo Estándar, además de tener paridad par y espín cero , [7] [8] dos atributos fundamentales de un bosón de Higgs. Esto también significa que es la primera partícula escalar elemental descubierta en la naturaleza. [33]
En marzo de 2013 se confirmó la existencia del bosón de Higgs y, por lo tanto, el concepto de algún tipo de campo de Higgs en todo el espacio está firmemente respaldado. [30] [32] [7] La presencia del campo, ahora confirmada por la investigación experimental, explica por qué algunas partículas fundamentales tienen masa (en reposo) , a pesar de las simetrías que controlan sus interacciones, lo que implica que deberían ser "sin masa". También resuelve varios otros enigmas de larga data, como la razón de la distancia extremadamente corta recorrida por los bosones de fuerza débil y, por lo tanto, el alcance extremadamente corto de la fuerza débil. A partir de 2018, una investigación en profundidad muestra que la partícula continúa comportándose de acuerdo con las predicciones para el bosón de Higgs del Modelo Estándar. Se necesitan más estudios para verificar con mayor precisión que la partícula descubierta tiene todas las propiedades predichas o si, como lo describen algunas teorías, existen múltiples bosones de Higgs. [34]
Actualmente se están investigando más a fondo la naturaleza y las propiedades de este campo, utilizando más datos recopilados en el LHC. [35]
Se han utilizado varias analogías para describir el campo de Higgs y el bosón, incluidas analogías con efectos de ruptura de simetría bien conocidos, como el arco iris y el prisma , los campos eléctricos y las ondas en la superficie del agua.
Se utilizan comúnmente otras analogías basadas en la resistencia de objetos macro que se mueven a través de medios (como personas que se mueven a través de multitudes o algunos objetos que se mueven a través de jarabe o melaza ), pero son engañosas, ya que el campo de Higgs en realidad no resiste a las partículas y el efecto de la masa no es causado por la resistencia.

En el Modelo Estándar, el bosón de Higgs es un bosón escalar masivo cuya masa debe determinarse experimentalmente. Se ha determinado que su masa es125,35 ± 0,15 GeV/ c 2 por CMS (2022) [36] y125,11 ± 0,11 GeV/ c 2 por ATLAS (2023). Es la única partícula que sigue siendo masiva incluso a energías muy altas. Tiene espín cero, paridad par (positiva) , no tiene carga eléctrica ni carga de color , y se acopla a la masa (interactúa con ella). [13] También es muy inestable y se desintegra en otras partículas casi inmediatamente a través de varias vías posibles.
El campo de Higgs es un campo escalar , con dos componentes neutros y dos cargados eléctricamente que forman un doblete complejo de simetría débil isospín SU(2). A diferencia de cualquier otro campo cuántico conocido, tiene un potencial de Sombrero . Esta forma significa que por debajo de energías extremadamente altas de aproximadamente159,5 ± 1,5 GeV [37] como los observados durante el primer picosegundo (10 −12 s) del Big Bang , el campo de Higgs en su estado fundamental necesita menos energía para tener una expectativa (valor) de vacío distinta de cero que un valor cero. Por lo tanto, en el universo actual, el campo de Higgs tiene un valor distinto de cero en todas partes (incluido el espacio vacío). Este valor distinto de cero, a su vez, rompe la simetría débil isospín SU(2) de la interacción electrodébil en todas partes. (Técnicamente, el valor de expectativa distinto de cero convierte los términos de acoplamiento de Yukawa del lagrangiano en términos de masa). Cuando esto sucede, tres componentes del campo de Higgs son "absorbidos" por los bosones de calibre SU(2) y U(1) (el " mecanismo de Higgs ") para convertirse en los componentes longitudinales de los ahora masivos bosones W y Z de la fuerza débil . El componente eléctricamente neutro restante se manifiesta como un bosón de Higgs o puede acoplarse por separado a otras partículas conocidas como fermiones (a través de acoplamientos de Yukawa ), lo que hace que estas también adquieran masa . [38]
La evidencia del campo de Higgs y sus propiedades ha sido extremadamente significativa por muchas razones. La importancia del bosón de Higgs radica en gran medida en que se puede examinar utilizando el conocimiento existente y la tecnología experimental, como una forma de confirmar y estudiar toda la teoría del campo de Higgs. [11] [12] Por el contrario, la prueba de que el campo de Higgs y el bosón no existían también habría sido significativa.
El bosón de Higgs valida el Modelo Estándar a través del mecanismo de generación de masa . A medida que se realicen mediciones más precisas de sus propiedades, se podrán sugerir o excluir extensiones más avanzadas. A medida que se desarrollen medios experimentales para medir los comportamientos e interacciones del campo, se podrá comprender mejor este campo fundamental. Si no se hubiera descubierto el campo de Higgs, habría sido necesario modificar o reemplazar el Modelo Estándar.
En relación con esto, entre los físicos existe la creencia generalizada de que es probable que exista una física "nueva" más allá del Modelo Estándar , y que en algún momento el Modelo Estándar será ampliado o reemplazado. El descubrimiento del Higgs, así como las numerosas colisiones medidas que se producen en el LHC, proporcionan a los físicos una herramienta sensible para buscar en sus datos cualquier evidencia de que el Modelo Estándar parece fallar, y podrían proporcionar evidencia considerable que oriente a los investigadores hacia futuros desarrollos teóricos.
Por debajo de una temperatura extremadamente alta, la ruptura de la simetría electrodébil hace que la interacción electrodébil se manifieste en parte como la fuerza débil de corto alcance , que es transportada por bosones de calibre masivos . En la historia del universo , se cree que la ruptura de la simetría electrodébil ocurrió aproximadamente 1 picosegundo (10 −12 s) después del Big Bang , cuando el universo estaba a una temperatura159,5 ± 1,5 GeV/ k B . [39] Esta ruptura de simetría es necesaria para la formación de átomos y otras estructuras, así como para las reacciones nucleares en estrellas, como el Sol . El campo de Higgs es responsable de esta ruptura de simetría.
El campo de Higgs es fundamental para generar las masas de los quarks y los leptones cargados (a través del acoplamiento de Yukawa) y los bosones de calibre W y Z (a través del mecanismo de Higgs).
El campo de Higgs no "crea" masa de la nada (lo que violaría la ley de conservación de la energía ), ni es el campo de Higgs responsable de la masa de todas las partículas. Por ejemplo, aproximadamente el 99% de la masa de los bariones ( partículas compuestas como el protón y el neutrón ), se debe en cambio a la energía de enlace cromodinámica cuántica , que es la suma de las energías cinéticas de los quarks y las energías de los gluones sin masa que median la interacción fuerte dentro de los bariones. [40] En las teorías basadas en el campo de Higgs, la propiedad de la "masa" es una manifestación de la energía potencial transferida a las partículas fundamentales cuando interactúan ("se acoplan") con el campo de Higgs, que había contenido esa masa en forma de energía . [41]
El campo de Higgs es el único campo escalar (espín 0) que se detecta; todos los demás campos fundamentales del Modelo Estándar son de espín 0. 1 /2 fermiones o bosones de espín 1. [k] Según Rolf-Dieter Heuer , director general del CERN cuando se descubrió el bosón de Higgs, esta prueba de existencia de un campo escalar es casi tan importante como el papel del Higgs en la determinación de la masa de otras partículas. Sugiere que otros campos escalares hipotéticos sugeridos por otras teorías, desde el inflatón hasta la quintaesencia , tal vez también podrían existir. [42] [43]
Se han realizado considerables investigaciones científicas sobre los posibles vínculos entre el campo de Higgs y el inflatón , un campo hipotético sugerido como la explicación de la expansión del espacio durante la primera fracción de segundo del universo (conocida como la " época inflacionaria "). Algunas teorías sugieren que un campo escalar fundamental podría ser responsable de este fenómeno; el campo de Higgs es un campo de este tipo, y su existencia ha dado lugar a artículos que analizan si también podría ser el inflatón responsable de esta expansión exponencial del universo durante el Big Bang . Estas teorías son muy provisionales y enfrentan problemas significativos relacionados con la unitaridad , pero pueden ser viables si se combinan con características adicionales como un gran acoplamiento no mínimo, un escalar de Brans-Dicke u otra física "nueva", y han recibido tratamientos que sugieren que los modelos de inflación de Higgs aún son de interés teóricamente.

En el Modelo Estándar, existe la posibilidad de que el estado subyacente de nuestro universo, conocido como el "vacío", sea duradero, pero no completamente estable . En este escenario, el universo tal como lo conocemos podría destruirse efectivamente al colapsar en un estado de vacío más estable . [45] [46] [47] [48] [49] Esto a veces se informó erróneamente como que el bosón de Higgs "acaba" con el universo. [l] Si las masas del bosón de Higgs y el quark top se conocen con mayor precisión, y el Modelo Estándar proporciona una descripción precisa de la física de partículas hasta energías extremas de la escala de Planck , entonces es posible calcular si el vacío es estable o simplemente duradero. [52] [53] [54] Una masa de Higgs de125–127 GeV/ c 2 parece estar extremadamente cerca del límite de estabilidad, pero una respuesta definitiva requiere mediciones mucho más precisas de la masa polar del quark top. [44] La nueva física puede cambiar esta imagen. [55]
Si las mediciones del bosón de Higgs sugieren que nuestro universo se encuentra dentro de un falso vacío de este tipo, entonces implicaría –muy probablemente en muchos miles de millones de años [56] [m] – que las fuerzas, partículas y estructuras del universo podrían dejar de existir como las conocemos (y ser reemplazadas por otras diferentes), si un verdadero vacío llegara a nuclearse . [56] [n] También sugiere que la función de autoacoplamiento del bosón de Higgs λ y su función β λ podrían ser muy cercanas a cero en la escala de Planck, con implicaciones "intrigantes", incluyendo teorías de la gravedad y la inflación basada en el bosón de Higgs. [44] : 218 [58] [59] Un futuro colisionador electrón-positrón sería capaz de proporcionar las mediciones precisas del quark top necesarias para tales cálculos. [44]
De manera más especulativa, el campo de Higgs también se ha propuesto como la energía del vacío , que en las energías extremas de los primeros momentos del Big Bang hizo que el universo fuera una especie de simetría sin rasgos distintivos de energía indiferenciada y extremadamente alta. En este tipo de especulación, el campo unificado único de una teoría de gran unificación se identifica como (o se modela sobre) el campo de Higgs, y es a través de sucesivas rupturas de simetría del campo de Higgs, o algún campo similar, en las transiciones de fase que surgen las fuerzas y los campos del universo actualmente conocidos. [60]
La relación (si la hay) entre el campo de Higgs y la densidad de energía del vacío observada actualmente en el universo también ha sido objeto de estudio científico. Como se ha observado, la densidad de energía del vacío actual es extremadamente cercana a cero, pero las densidades de energía predichas a partir del campo de Higgs, la supersimetría y otras teorías actuales son típicamente muchos órdenes de magnitud mayores. No está claro cómo se deben conciliar. Este problema de la constante cosmológica sigue siendo un importante problema sin respuesta en la física.
Los físicos de partículas estudian la materia hecha de partículas fundamentales cuyas interacciones están mediadas por partículas de intercambio –bosones gauge– que actúan como portadores de fuerza . A principios de la década de 1960 se habían descubierto o propuesto varias de estas partículas, junto con teorías que sugerían cómo se relacionaban entre sí, algunas de las cuales ya habían sido reformuladas como teorías de campo en las que los objetos de estudio no son partículas y fuerzas, sino campos cuánticos y sus simetrías . [61] : 150 Sin embargo, los intentos de producir modelos de campo cuántico para dos de las cuatro fuerzas fundamentales conocidas –la fuerza electromagnética y la fuerza nuclear débil– y luego unificar estas interacciones , todavía no tuvieron éxito.
Un problema conocido era que los enfoques invariantes de calibre , incluidos los modelos no abelianos como la teoría de Yang-Mills (1954), que eran muy prometedores para las teorías unificadas, también parecían predecir que las partículas masivas conocidas no tenían masa. [24] El teorema de Goldstone , relacionado con las simetrías continuas dentro de algunas teorías, también parecía descartar muchas soluciones obvias, [62] ya que parecía mostrar que también tendrían que existir partículas de masa cero conocidas como bosones de Goldstone que simplemente "no se vieran". [63] Según Guralnik , los físicos "no entendían" cómo se podían superar estos problemas. [63]

El físico de partículas y matemático Peter Woit resumió el estado de la investigación en ese momento:
El trabajo de Yang y Mills sobre la teoría de gauge no abeliana tenía un enorme problema: en la teoría de perturbaciones hay partículas sin masa que no corresponden a nada de lo que vemos. Una forma de deshacerse de este problema es ahora bastante bien entendida: el fenómeno de confinamiento realizado en QCD , donde las interacciones fuertes se deshacen de los estados de "gluón" sin masa a grandes distancias. A principios de los años sesenta, la gente había comenzado a entender otra fuente de partículas sin masa: la ruptura espontánea de la simetría de una simetría continua. Lo que Philip Anderson se dio cuenta y elaboró en el verano de 1962 fue que, cuando tienes simetría de gauge y ruptura espontánea de la simetría, el modo de Nambu-Goldstone sin masa [que da lugar a los bosones de Goldstone] puede combinarse con los modos de campo de gauge sin masa [que dan lugar a los bosones de gauge sin masa] para producir un campo vectorial masivo físico [bosones de gauge con masa]. Esto es lo que sucede en la superconductividad , un tema sobre el que Anderson fue (y es) uno de los principales expertos. [24] [texto condensado]
El mecanismo de Higgs es un proceso por el cual los bosones vectoriales pueden adquirir masa en reposo sin romper explícitamente la invariancia de calibre , como un subproducto de la ruptura espontánea de la simetría . [64] [65] Inicialmente, la teoría matemática detrás de la ruptura espontánea de la simetría fue concebida y publicada dentro de la física de partículas por Yoichiro Nambu en 1960 [66] (y algo anticipada por Ernst Stueckelberg en 1938 [67] ), y el concepto de que tal mecanismo podría ofrecer una posible solución para el "problema de la masa" fue sugerido originalmente en 1962 por Philip Anderson, quien previamente había escrito artículos sobre la simetría rota y sus resultados en la superconductividad. [68] Anderson concluyó en su artículo de 1963 sobre la teoría de Yang-Mills que "considerando el análogo superconductor... [e]stos dos tipos de bosones parecen capaces de cancelarse entre sí... dejando bosones de masa finita"), [69] [26] y en marzo de 1964, Abraham Klein y Benjamin Lee demostraron que el teorema de Goldstone podía evitarse de esta manera al menos en algunos casos no relativistas, y especularon que podría ser posible en casos verdaderamente relativistas. [25]
Estos enfoques fueron desarrollados rápidamente en un modelo relativista completo , de forma independiente y casi simultánea, por tres grupos de físicos: por François Englert y Robert Brout en agosto de 1964; [70] por Peter Higgs en octubre de 1964; [71] y por Gerald Guralnik , Carl Hagen y Tom Kibble (GHK) en noviembre de 1964. [72] Higgs también escribió una respuesta corta, pero importante, [64] publicada en septiembre de 1964 a una objeción de Gilbert , [73] que mostraba que si se calculaba dentro del medidor de radiación, el teorema de Goldstone y la objeción de Gilbert se volverían inaplicables. [o] Higgs luego describió la objeción de Gilbert como la que motivó su propio artículo. [74] Las propiedades del modelo fueron consideradas más a fondo por Guralnik en 1965, [75] por Higgs en 1966, [76] por Kibble en 1967, [77] y más adelante por GHK en 1967. [78] Los tres artículos originales de 1964 demostraron que cuando una teoría de calibre se combina con un campo escalar cargado adicional que rompe espontáneamente la simetría, los bosones de calibre pueden adquirir consistentemente una masa finita. [64] [65] [79] En 1967, Steven Weinberg [80] y Abdus Salam [81] mostraron independientemente cómo un mecanismo de Higgs podría usarse para romper la simetría electrodébil del modelo unificado de Sheldon Glashow para las interacciones débiles y electromagnéticas , [82] (en sí mismo una extensión del trabajo de Schwinger ), formando lo que se convirtió en el Modelo Estándar de la física de partículas. Weinberg fue el primero en observar que esto también proporcionaría términos de masa para los fermiones. [83] [p]
Al principio, estos artículos seminales sobre la ruptura espontánea de simetrías de calibración fueron ignorados en gran medida, porque se creía ampliamente que las teorías de calibración (no abelianas) en cuestión eran un callejón sin salida, y en particular que no podían ser renormalizadas . En 1971-72, Martinus Veltman y Gerard 't Hooft demostraron que la renormalización de Yang-Mills era posible en dos artículos que cubrían campos sin masa, y luego campos masivos. [83] Su contribución, y el trabajo de otros en el grupo de renormalización , incluido el trabajo teórico "sustancial" de los físicos rusos Ludvig Faddeev , Andrei Slavnov , Efim Fradkin e Igor Tyutin [84] - fue finalmente "enormemente profundo e influyente", [85] pero incluso con todos los elementos clave de la teoría final publicada, todavía casi no hubo un interés más amplio. Por ejemplo, Coleman encontró en un estudio que "esencialmente nadie prestó atención" al artículo de Weinberg antes de 1971 [86] y discutido por David Politzer en su discurso Nobel de 2004 [85] – ahora el más citado en física de partículas [87] – e incluso en 1970 según Politzer, la enseñanza de Glashow sobre la interacción débil no contenía ninguna mención del trabajo de Weinberg, Salam o el propio Glashow. [85] En la práctica, afirma Politzer, casi todos aprendieron de la teoría debido al físico Benjamin Lee , quien combinó el trabajo de Veltman y 't Hooft con ideas de otros, y popularizó la teoría completa. [85] De esta manera, a partir de 1971, el interés y la aceptación "explotaron" [85] y las ideas fueron rápidamente absorbidas por la corriente principal. [83] [85]
La teoría electrodébil resultante y el Modelo Estándar han predicho con precisión (entre otras cosas) las corrientes neutras débiles , los tres bosones , los quarks top y charm , y con gran precisión, la masa y otras propiedades de algunos de ellos. [f] Muchos de los implicados acabaron ganando premios Nobel u otros premios de renombre. Un artículo de 1974 y una revisión exhaustiva en Reviews of Modern Physics comentaron que "aunque nadie dudaba de la corrección [matemática] de estos argumentos, nadie creía del todo que la naturaleza fuera lo suficientemente diabólicamente inteligente como para sacar ventaja de ellos", [88] añadiendo que la teoría había producido hasta ahora respuestas precisas que concordaban con la experimentación, pero se desconocía si la teoría era fundamentalmente correcta. [89] En 1986 y de nuevo en la década de 1990 se hizo posible escribir que entender y probar el sector de Higgs del Modelo Estándar era "el problema central hoy en día en la física de partículas". [14] [15]
Los tres artículos escritos en 1964 fueron reconocidos como artículos de referencia durante la celebración del 50 aniversario de Physical Review Letters . [79] Sus seis autores también fueron galardonados con el Premio JJ Sakurai 2010 de Física Teórica de Partículas por este trabajo. [90] (También surgió una controversia el mismo año, porque en el caso de un Premio Nobel solo se podía reconocer a hasta tres científicos, y seis eran acreditados por los artículos. [91] ) Dos de los tres artículos de PRL (de Higgs y de GHK) contenían ecuaciones para el campo hipotético que eventualmente se conocería como el campo de Higgs y su cuanto hipotético , el bosón de Higgs. [71] [72] El artículo posterior de Higgs de 1966 mostró el mecanismo de desintegración del bosón; solo un bosón masivo puede desintegrarse y las desintegraciones pueden probar el mecanismo. [ cita requerida ]
En el artículo de Higgs, el bosón es masivo, y en una oración final Higgs escribe que "una característica esencial" de la teoría "es la predicción de multipletes incompletos de bosones escalares y vectoriales ". [71] ( Frank Close comenta que los teóricos de calibre de la década de 1960 se centraron en el problema de los bosones vectoriales sin masa , y la existencia implícita de un bosón escalar masivo no se consideró importante; solo Higgs lo abordó directamente. [92] : 154, 166, 175 ) En el artículo de GHK, el bosón no tiene masa y está desacoplado de los estados masivos. [72] En revisiones de 2009 y 2011, Guralnik afirma que en el modelo GHK el bosón solo no tiene masa en una aproximación de orden más bajo, pero no está sujeto a ninguna restricción y adquiere masa en órdenes superiores, y agrega que el artículo de GHK fue el único en demostrar que no hay bosones de Goldstone sin masa en el modelo y en dar un análisis completo del mecanismo general de Higgs. [63] [93] Los tres llegaron a conclusiones similares, a pesar de sus enfoques muy diferentes: el artículo de Higgs utilizó esencialmente técnicas clásicas, el de Englert y Brout implicó calcular la polarización del vacío en la teoría de perturbaciones alrededor de un estado de vacío de ruptura de simetría asumido, y GHK utilizó el formalismo de operadores y las leyes de conservación para explorar en profundidad las formas en que se puede evitar el teorema de Goldstone. [64] Algunas versiones de la teoría predijeron más de un tipo de campos y bosones de Higgs, y se consideraron modelos alternativos "sin Higgs" hasta el descubrimiento del bosón de Higgs.
Para producir bosones de Higgs, se aceleran dos haces de partículas a energías muy altas y se les permite colisionar dentro de un detector de partículas . Ocasionalmente, aunque raramente, se creará un bosón de Higgs fugazmente como parte de los subproductos de la colisión. Debido a que el bosón de Higgs se desintegra muy rápidamente, los detectores de partículas no pueden detectarlo directamente. En cambio, los detectores registran todos los productos de desintegración (la firma de desintegración ) y a partir de los datos se reconstruye el proceso de desintegración. Si los productos de desintegración observados coinciden con un posible proceso de desintegración (conocido como canal de desintegración ) de un bosón de Higgs, esto indica que puede haberse creado un bosón de Higgs. En la práctica, muchos procesos pueden producir firmas de desintegración similares. Afortunadamente, el Modelo Estándar predice con precisión la probabilidad de que ocurra cada uno de estos procesos, y cada uno de los procesos conocidos. Por lo tanto, si el detector detecta más firmas de desintegración que coinciden consistentemente con un bosón de Higgs de lo que se esperaría de otra manera si los bosones de Higgs no existieran, entonces esto sería una evidencia sólida de que el bosón de Higgs existe.
Como la producción del bosón de Higgs en una colisión de partículas es muy poco frecuente (1 en 10 mil millones en el LHC), [q] y muchos otros eventos de colisión posibles pueden tener firmas de desintegración similares, es necesario analizar los datos de cientos de billones de colisiones y deben "mostrar la misma imagen" antes de poder llegar a una conclusión sobre la existencia del bosón de Higgs. Para concluir que se ha encontrado una nueva partícula, los físicos de partículas requieren que el análisis estadístico de dos detectores de partículas independientes indique cada uno que hay menos de una probabilidad en un millón de que las firmas de desintegración observadas se deban solo a eventos aleatorios de fondo del Modelo Estándar, es decir, que el número observado de eventos sea más de cinco desviaciones estándar (sigma) diferente del esperado si no hubiera una nueva partícula. Más datos de colisión permiten una mejor confirmación de las propiedades físicas de cualquier nueva partícula observada, y permite a los físicos decidir si es de hecho un bosón de Higgs como lo describe el Modelo Estándar o alguna otra partícula nueva hipotética.
Para encontrar el bosón de Higgs, se necesitaba un potente acelerador de partículas , porque los bosones de Higgs podrían no verse en experimentos de menor energía. El colisionador necesitaba tener una alta luminosidad para garantizar que se vieran suficientes colisiones para poder sacar conclusiones. Finalmente, se necesitaban instalaciones informáticas avanzadas para procesar la enorme cantidad de datos (25 petabytes por año a partir de 2012) producidos por las colisiones. [96] Para el anuncio del 4 de julio de 2012, se construyó en el CERN un nuevo colisionador conocido como el Gran Colisionador de Hadrones con una energía de colisión final planificada de 14 TeV , más de siete veces la de cualquier colisionador anterior, y más de 300 billones (Las colisiones protón-protón del LHC fueron analizadas por el LHC Computing Grid , la red informática más grande del mundo ( a partir de 2012), que comprende más de 170 instalaciones informáticas en una red mundial en 36 países. [96] [ 97] [98]
La primera búsqueda extensa del bosón de Higgs se llevó a cabo en el Gran Colisionador de Electrones y Positrones (LEP) del CERN en la década de 1990. Al final de su servicio en 2000, el LEP no había encontrado evidencia concluyente del bosón de Higgs. [r] Esto implicaba que si el bosón de Higgs existiera, tendría que ser más pesado que114,4 GeV/ c2 . [ 99]
La búsqueda continuó en el Fermilab de Estados Unidos, donde el Tevatron (el colisionador que descubrió el quark top en 1995) había sido mejorado para este propósito. No había garantía de que el Tevatron pudiera encontrar el bosón de Higgs, pero era el único supercolisionador que estaba operativo ya que el Gran Colisionador de Hadrones (LHC) todavía estaba en construcción y el Supercolisionador Superconductor planeado se había cancelado en 1993 y nunca se completó. El Tevatron solo pudo excluir más rangos para la masa del bosón de Higgs, y se cerró el 30 de septiembre de 2011 porque ya no podía seguir el ritmo del LHC. El análisis final de los datos excluyó la posibilidad de un bosón de Higgs con una masa entre 100 y 150 μg/cm2.147 GeV/ c 2 y180 GeV/ c 2 . Además, hubo un pequeño (pero no significativo) exceso de eventos que posiblemente indicaban un bosón de Higgs con una masa entre115 GeV/ c 2 y140 GeV/ c2 . [ 100]
El Gran Colisionador de Hadrones del CERN, en Suiza, fue diseñado específicamente para poder confirmar o descartar la existencia del bosón de Higgs. Construido en un túnel de 27 km bajo tierra cerca de Ginebra, originalmente habitado por LEP, fue diseñado para colisionar dos haces de protones, inicialmente a energías de3,5 TeV por haz (7 TeV en total), o casi 3,6 veces la del Tevatron, y ampliable a 2 × 7 TeV (14 TeV en total) en el futuro. La teoría sugería que si el bosón de Higgs existía, las colisiones a estos niveles de energía deberían poder revelarlo. Como uno de los instrumentos científicos más complicados jamás construidos, su disponibilidad operativa se retrasó durante 14 meses debido a un evento de extinción de imanes nueve días después de sus pruebas inaugurales, causado por una conexión eléctrica defectuosa que dañó más de 50 imanes superconductores y contaminó el sistema de vacío. [101] [102] [103]
La recopilación de datos en el LHC finalmente comenzó en marzo de 2010. [104] Para diciembre de 2011, los dos detectores de partículas principales del LHC, ATLAS y CMS , habían reducido el rango de masa en el que podría existir el Higgs a alrededor de116–130 GeV/ c 2 (ATLAS) y115–127 GeV/ c 2 (CMS). [105] [106] También había habido una serie de excesos de eventos prometedores que se habían "evaporado" y demostrado ser nada más que fluctuaciones aleatorias. Sin embargo, desde aproximadamente mayo de 2011, [107] ambos experimentos habían visto entre sus resultados, la lenta aparición de un exceso pequeño pero constante de firmas de desintegración gamma y de 4 leptones y varias otras desintegraciones de partículas, todas apuntando a una nueva partícula con una masa de alrededor de 115–127 GeV/ c 2 (CMS).125 GeV/ c 2 . [107] Alrededor de noviembre de 2011, los datos anómalos enEl tamaño de 125 GeV/ c 2 se estaba volviendo "demasiado grande para ignorarlo" (aunque todavía estaba lejos de ser concluyente), y los líderes de equipo tanto de ATLAS como de CMS sospechaban en privado que podrían haber encontrado el bosón de Higgs. [107] El 28 de noviembre de 2011, en una reunión interna de los dos líderes de equipo y el director general del CERN, los últimos análisis se discutieron fuera de sus equipos por primera vez, lo que sugiere que tanto ATLAS como CMS podrían estar convergiendo en un posible resultado compartido en125 GeV/ c 2 , y comenzaron los preparativos iniciales en caso de un hallazgo exitoso. [107] Si bien esta información no se conocía públicamente en ese momento, la reducción del posible rango del Higgs a alrededor de115–130 GeV/2 y la observación repetida de excesos de eventos pequeños pero consistentes en múltiples canales tanto en ATLAS como en CMS en elLos datos de la región de 124-126 GeV/ c 2 (descritos como "pistas tentadoras" de alrededor de 2-3 sigma) eran de conocimiento público y despertaban "mucho interés". [108] Por lo tanto, se esperaba ampliamente que a fines de 2011 el LHC proporcionaría datos suficientes para excluir o confirmar el hallazgo de un bosón de Higgs para fines de 2012, cuando se hubieran examinado sus datos de colisión de 2012 (con una energía de colisión ligeramente superior de 8 TeV). [108] [109]
El 22 de junio de 2012, el CERN anunció un próximo seminario que cubriría hallazgos tentativos para 2012, [113] [114] y poco después (alrededor del 1 de julio de 2012 según un análisis del rumor que se extendía en las redes sociales [115] ) comenzaron a difundirse rumores en los medios de que esto incluiría un anuncio importante, pero no estaba claro si esto sería una señal más fuerte o un descubrimiento formal. [116] [117] La especulación escaló a un tono "febril" cuando surgieron informes de que Peter Higgs , quien propuso la partícula, asistiría al seminario, [118] [119] y que "cinco físicos destacados" habían sido invitados -generalmente se cree que significa los cinco autores vivos de 1964- con Higgs, Englert, Guralnik, Hagen asistiendo y Kibble confirmando su invitación (Brout había muerto en 2011). [120]
El 4 de julio de 2012, ambos experimentos del CERN anunciaron que habían hecho independientemente el mismo descubrimiento: [121] CMS de un bosón previamente desconocido con masa125,3 ± 0,6 GeV/ c 2 [122] [123] y ATLAS de un bosón con masa126,0 ± 0,6 GeV/ c 2 . [124] [125] Utilizando el análisis combinado de dos tipos de interacción (conocidos como "canales"), ambos experimentos alcanzaron independientemente una significancia local de 5 sigma, lo que implica que la probabilidad de obtener al menos un resultado tan fuerte por pura casualidad es inferior a una en tres millones. Cuando se tuvieron en cuenta canales adicionales, la significancia de CMS se redujo a 4,9 sigma. [123]
Los dos equipos habían estado trabajando "a ciegas" entre sí desde finales de 2011 o principios de 2012, [107] lo que significa que no discutieron sus resultados entre sí, lo que proporcionó certeza adicional de que cualquier hallazgo común era una validación genuina de una partícula. [96] Este nivel de evidencia, confirmado independientemente por dos equipos y experimentos separados, cumple con el nivel formal de prueba requerido para anunciar un descubrimiento confirmado.
El 31 de julio de 2012, la colaboración ATLAS presentó un análisis de datos adicional sobre la "observación de una nueva partícula", incluidos datos de un tercer canal, que mejoró la significancia a 5,9 sigma (1 en 588 millones de posibilidades de obtener al menos una evidencia tan sólida solo con efectos de fondo aleatorios) y masa 126,0 ± 0,4 (stat) ± 0,4 (sys) GeV/ c 2 , [125] y CMS mejoró la significancia a 5 sigma y masa 125,3 ± 0,4 (stat) ± 0,5 (sys) GeV/ c 2 . [122]
Tras el descubrimiento de 2012, aún no se había confirmado si elLa partícula de 125 GeV/ c 2 era un bosón de Higgs. Por un lado, las observaciones se mantuvieron consistentes con la idea de que la partícula observada era el bosón de Higgs del Modelo Estándar, y la partícula se desintegró en al menos algunos de los canales predichos. Además, las tasas de producción y las proporciones de ramificación de los canales observados coincidieron ampliamente con las predicciones del Modelo Estándar dentro de las incertidumbres experimentales. Sin embargo, las incertidumbres experimentales actuales aún dejaban lugar a explicaciones alternativas, lo que significa que un anuncio del descubrimiento de un bosón de Higgs habría sido prematuro. [126] Para permitir más oportunidades para la recopilación de datos, el cierre propuesto del LHC en 2012 y la actualización 2013-14 se pospusieron siete semanas en 2013. [127]
En noviembre de 2012, en una conferencia en Kioto, los investigadores dijeron que la evidencia reunida desde julio estaba coincidiendo más con el Modelo Estándar básico que con sus alternativas, con un rango de resultados para varias interacciones que coincidían con las predicciones de esa teoría. [128] El físico Matt Strassler destacó la evidencia "considerable" de que la nueva partícula no es una partícula pseudoescalar de paridad negativa (consistente con este hallazgo requerido para un bosón de Higgs), la "evaporación" o la falta de mayor importancia para indicios previos de hallazgos no pertenecientes al Modelo Estándar, las interacciones esperadas del Modelo Estándar con los bosones W y Z , la ausencia de "nuevas implicaciones significativas" a favor o en contra de la supersimetría y, en general, ninguna desviación significativa hasta la fecha de los resultados esperados de un bosón de Higgs del Modelo Estándar. [s] Sin embargo, algunos tipos de extensiones del Modelo Estándar también mostrarían resultados muy similares; [130] por lo que los comentaristas señalaron que, basándose en otras partículas que todavía se están entendiendo mucho después de su descubrimiento, puede llevar años estar seguro y décadas comprender completamente la partícula que se ha encontrado. [128] [s]
Estos hallazgos significaron que a partir de enero de 2013, los científicos estaban muy seguros de haber encontrado una partícula desconocida de masa ~ 125 GeV/ c 2 , y no se habían dejado engañar por un error experimental o un resultado casual. También estaban seguros, a partir de las observaciones iniciales, de que la nueva partícula era algún tipo de bosón. Los comportamientos y propiedades de la partícula, examinados hasta el momento desde julio de 2012, también parecían bastante cercanos a los comportamientos esperados de un bosón de Higgs. Aun así, todavía podría haber sido un bosón de Higgs o algún otro bosón desconocido, ya que las pruebas futuras podrían mostrar comportamientos que no coincidan con un bosón de Higgs, por lo que a diciembre de 2012 el CERN todavía solo declaró que la nueva partícula era "coherente con" el bosón de Higgs, [30] [32] y los científicos aún no dijeron positivamente que fuera el bosón de Higgs. [131] A pesar de esto, a fines de 2012, informes generalizados de los medios anunciaron (incorrectamente) que se había confirmado un bosón de Higgs durante el año. [137]
En enero de 2013, el director general del CERN, Rolf-Dieter Heuer, afirmó que, basándose en el análisis de datos hasta la fecha, podría ser posible obtener una respuesta "hacia" mediados de 2013, [ 138] y el vicepresidente de física del Laboratorio Nacional de Brookhaven afirmó en febrero de 2013 que una respuesta "definitiva" podría requerir "unos años más" después del reinicio del colisionador en 2015. [139] A principios de marzo de 2013, el director de investigación del CERN, Sergio Bertolucci, afirmó que confirmar el espín 0 era el principal requisito restante para determinar si la partícula es al menos algún tipo de bosón de Higgs. [140]
El 14 de marzo de 2013 el CERN confirmó lo siguiente:
El CMS y el ATLAS han comparado varias opciones para la paridad de espín de esta partícula, y todas ellas prefieren la ausencia de espín y la paridad par [dos criterios fundamentales de un bosón de Higgs compatibles con el Modelo Estándar]. Esto, junto con las interacciones medidas de la nueva partícula con otras partículas, indica firmemente que se trata de un bosón de Higgs. [7]
Esto también convierte a la partícula en la primera partícula escalar elemental descubierta en la naturaleza. [33]
Los siguientes son ejemplos de pruebas utilizadas para confirmar que la partícula descubierta es el bosón de Higgs: [s] [13]
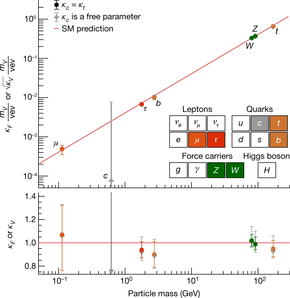
En julio de 2017, el CERN confirmó que todas las mediciones siguen coincidiendo con las predicciones del Modelo Estándar y denominó a la partícula descubierta simplemente "el bosón de Higgs". [35] A partir de 2019, el Gran Colisionador de Hadrones ha seguido produciendo hallazgos que confirman la comprensión de 2013 del campo y la partícula de Higgs. [147] [148]
El trabajo experimental del LHC desde su reinicio en 2015 ha incluido el sondeo del campo y el bosón de Higgs con un mayor nivel de detalle, y la confirmación de si las predicciones menos comunes eran correctas. En particular, la exploración desde 2015 ha proporcionado evidencia sólida de la desintegración directa predicha en fermiones como pares de quarks bottom (3,6 σ) –descrita como un "hito importante" en la comprensión de su corta vida y otras desintegraciones raras– y también para confirmar la desintegración en pares de leptones tau (5,9 σ). Esto fue descrito por el CERN como "de suma importancia para establecer el acoplamiento del bosón de Higgs a los leptones y representa un paso importante hacia la medición de sus acoplamientos a los fermiones de tercera generación, las copias muy pesadas de los electrones y quarks, cuyo papel en la naturaleza es un profundo misterio". [35] Los resultados publicados al 19 de marzo de 2018 a 13 TeV para ATLAS y CMS tenían sus mediciones de la masa del Higgs en124,98 ± 0,28 GeV/ c 2 y125,26 ± 0,21 GeV/ c 2 respectivamente.
En julio de 2018, los experimentos ATLAS y CMS informaron haber observado la desintegración del bosón de Higgs en un par de quarks bottom, lo que representa aproximadamente el 60% de todas sus desintegraciones. [149] [150] [151]
La invariancia de calibre es una propiedad importante de las teorías de partículas modernas como el Modelo Estándar , en parte debido a su éxito en otras áreas de la física fundamental como el electromagnetismo y la interacción fuerte ( cromodinámica cuántica ). Sin embargo, antes de que Sheldon Glashow extendiera los modelos de unificación electrodébil en 1961, hubo grandes dificultades para desarrollar teorías de calibre para la fuerza nuclear débil o una posible interacción electrodébil unificada . Los fermiones con un término de masa violarían la simetría de calibre y, por lo tanto, no pueden ser invariantes de calibre. (Esto se puede ver examinando el Lagrangiano de Dirac para un fermión en términos de componentes zurdos y diestros; encontramos que ninguna de las partículas de espín-mitad podría invertir la helicidad como se requiere para la masa, por lo que deben ser sin masa. [t] ) Se observa que los bosones W y Z tienen masa, pero un término de masa de bosón contiene términos que dependen claramente de la elección del calibre y, por lo tanto, estas masas tampoco pueden ser invariantes de calibre. Por lo tanto, parece que ninguno de los fermiones o bosones del modelo estándar podría "comenzar" con la masa como propiedad intrínseca, excepto abandonando la invariancia de norma. Si se hubiera de conservar la invariancia de norma, entonces estas partículas tendrían que estar adquiriendo su masa mediante algún otro mecanismo o interacción.
Además, las soluciones basadas en la ruptura espontánea de la simetría parecieron fallar, aparentemente un resultado inevitable del teorema de Goldstone . Debido a que no hay un costo de energía potencial para moverse alrededor del "valle circular" del plano complejo responsable de la ruptura espontánea de la simetría, la excitación cuántica resultante es energía cinética pura y, por lo tanto, un bosón sin masa ("bosón de Goldstone"), que a su vez implica una nueva fuerza de largo alcance. Pero tampoco se detectaron nuevas fuerzas de largo alcance o partículas sin masa. Por lo tanto, lo que le daba a estas partículas su masa no tenía que "romper" la invariancia de calibre como base para otras partes de las teorías donde funcionaba bien, y no tenía que requerir o predecir partículas sin masa inesperadas o fuerzas de largo alcance que en realidad no parecían existir en la naturaleza.
Una solución a todos estos problemas superpuestos llegó del descubrimiento de un caso límite previamente inadvertido oculto en las matemáticas del teorema de Goldstone: [o] bajo ciertas condiciones podría ser teóricamente posible romper una simetría sin alterar la invariancia de norma y sin nuevas partículas o fuerzas sin masa, y teniendo resultados "sensibles" ( renormalizables ) matemáticamente. Esto se conoció como el mecanismo de Higgs .

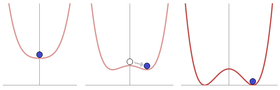
El Modelo Estándar plantea la hipótesis de un campo que es responsable de este efecto, llamado campo de Higgs (símbolo: ), que tiene la propiedad inusual de una amplitud distinta de cero en su estado fundamental ; es decir, un valor de expectativa de vacío distinto de cero . Puede tener este efecto debido a su potencial inusual en forma de "sombrero mexicano" cuyo "punto" más bajo no está en su "centro". En términos simples, a diferencia de todos los demás campos conocidos, el campo de Higgs requiere menos energía para tener un valor distinto de cero que un valor cero, por lo que termina teniendo un valor distinto de cero en todas partes . Por debajo de un cierto nivel de energía extremadamente alto, la existencia de esta expectativa de vacío distinta de cero rompe espontáneamente la simetría de calibre electrodébil , lo que a su vez da lugar al mecanismo de Higgs y desencadena la adquisición de masa por parte de las partículas que interactúan con el campo. Este efecto se produce porque los componentes del campo escalar del campo de Higgs son "absorbidos" por los bosones masivos como grados de libertad , y se acoplan a los fermiones a través del acoplamiento de Yukawa , produciendo así los términos de masa esperados. Cuando la simetría se rompe en estas condiciones, los bosones de Goldstone que surgen interactúan con el campo de Higgs (y con otras partículas capaces de interactuar con el campo de Higgs) en lugar de convertirse en nuevas partículas sin masa. Los problemas insolubles de ambas teorías subyacentes se "neutralizan" mutuamente, y el resultado residual es que las partículas elementales adquieren una masa consistente en función de la fuerza con la que interactúan con el campo de Higgs. Es el proceso más simple conocido capaz de dar masa a los bosones de gauge y al mismo tiempo seguir siendo compatible con las teorías de gauge . [152] Su quantum sería un bosón escalar , conocido como bosón de Higgs. [153]
El mecanismo de Higgs propuesto surgió como resultado de teorías propuestas para explicar observaciones en superconductividad . Un superconductor no permite la penetración de campos magnéticos externos (el efecto Meissner ). Esta extraña observación implica que, de alguna manera, el campo electromagnético se vuelve de corto alcance durante este fenómeno. Surgieron teorías exitosas para explicar esto durante la década de 1950, primero para los fermiones ( teoría de Ginzburg-Landau , 1950), y luego para los bosones ( teoría BCS , 1957).
En estas teorías, la superconductividad se interpreta como el resultado de un campo de condensado cargado . Inicialmente, el valor del condensado no tiene ninguna dirección preferida, lo que implica que es escalar, pero su fase es capaz de definir un calibre, en teorías de campo basadas en el calibre. Para ello, el campo debe estar cargado. Un campo escalar cargado también debe ser complejo (o, dicho de otro modo, debe contener al menos dos componentes y una simetría capaz de rotar cada uno de ellos en el otro u otros). En la teoría de calibre ingenua, una transformación de calibre de un condensado suele rotar la fase. Pero en estas circunstancias, en cambio, fija una elección preferida de fase. Sin embargo, resulta que fijar la elección del calibre de modo que el condensado tenga la misma fase en todas partes también hace que el campo electromagnético gane un término adicional. Este término adicional hace que el campo electromagnético se vuelva de corto alcance.
Una vez que se llamó la atención sobre esta teoría dentro de la física de partículas, los paralelismos quedaron claros. Un cambio del campo electromagnético, que normalmente es de largo alcance, a uno de corto alcance, dentro de una teoría invariante de norma, era exactamente el efecto necesario buscado para los bosones de fuerza débil (porque una fuerza de largo alcance tiene bosones de norma sin masa, y una fuerza de corto alcance implica bosones de norma masivos, lo que sugiere que un resultado de esta interacción es que los bosones de norma del campo adquirieron masa, o un efecto similar y equivalente). Las características de un campo requerido para hacer esto también estaban bastante bien definidas: tendría que ser un campo escalar cargado, con al menos dos componentes, y complejo para soportar una simetría capaz de rotarlos entre sí. [u]
El modelo estándar mínimo descrito anteriormente es el modelo más simple conocido para el mecanismo de Higgs con un solo campo de Higgs. Sin embargo, también es posible un sector de Higgs extendido con dobletes o tripletes de partículas de Higgs adicionales, y muchas extensiones del modelo estándar tienen esta característica. El sector de Higgs no mínimo favorecido por la teoría son los modelos de dos dobletes de Higgs (2HDM), que predicen la existencia de un quinteto de partículas escalares: dos bosones de Higgs neutros CP-pares h 0 y H 0 , un bosón de Higgs neutro CP-impar A 0 y dos partículas de Higgs cargadas H ± . La supersimetría ("SUSY") también predice relaciones entre las masas de los bosones de Higgs y las masas de los bosones de calibración, y podría dar cabida a unaBosón de Higgs neutro de 125 GeV/ c 2 .
El método clave para distinguir entre estos diferentes modelos implica el estudio de las interacciones de las partículas ("acoplamiento") y los procesos exactos de desintegración ("coeficientes de ramificación"), que pueden medirse y probarse experimentalmente en colisiones de partículas. En el modelo 2HDM Tipo-I, un doblete de Higgs se acopla a los quarks up y down, mientras que el segundo doblete no se acopla a los quarks. Este modelo tiene dos límites interesantes, en los que el Higgs más ligero se acopla sólo a los fermiones ("gauge- fóbico ") o sólo a los bosones gauge ("fermiofóbico"), pero no a ambos. En el modelo 2HDM Tipo-II, un doblete de Higgs sólo se acopla a los quarks de tipo up, el otro sólo se acopla a los quarks de tipo down. [154] El Modelo Estándar Supersimétrico Mínimo (MSSM) , muy investigado , incluye un sector de Higgs 2HDM Tipo-II, por lo que podría ser refutado por la evidencia de un Higgs 2HDM Tipo-I. [ cita requerida ]
En otros modelos, el escalar de Higgs es una partícula compuesta. Por ejemplo, en technicolor, el papel del campo de Higgs lo desempeñan pares de fermiones fuertemente ligados llamados techniquarks . Otros modelos presentan pares de quarks top (véase condensado de quarks top ). En otros modelos, no existe ningún campo de Higgs y la simetría electrodébil se rompe utilizando dimensiones adicionales. [155] [156]

El Modelo Estándar deja la masa del bosón de Higgs como un parámetro a medir, en lugar de un valor a calcular. Esto se considera teóricamente insatisfactorio, en particular porque las correcciones cuánticas (relacionadas con las interacciones con partículas virtuales ) aparentemente deberían hacer que la partícula de Higgs tenga una masa inmensamente mayor que la observada, pero al mismo tiempo el Modelo Estándar requiere una masa del orden de 100 a 1000 GeV/ c 2 para asegurar la unitaridad (en este caso, para unitarizar la dispersión longitudinal de bosones vectoriales). [157] Para reconciliar estos puntos parece necesario explicar por qué hay una cancelación casi perfecta que da como resultado la masa visible de ~ 125 GeV/ c 2 , y no está claro cómo hacer esto. Debido a que la fuerza débil es aproximadamente 10 32 veces más fuerte que la gravedad, y (vinculado a esto) la masa del bosón de Higgs es mucho menor que la masa de Planck o la energía de gran unificación , parece que hay alguna conexión subyacente o razón para estas observaciones que es desconocida y no está descrita por el Modelo Estándar, o algún ajuste fino inexplicable y extremadamente preciso de los parámetros; sin embargo, en la actualidad ninguna de estas explicaciones está probada. Esto se conoce como un problema de jerarquía . [158] Más ampliamente, el problema de la jerarquía equivale a la preocupación de que una futura teoría de partículas fundamentales e interacciones no debería tener ajustes finos excesivos o cancelaciones indebidamente delicadas, y debería permitir que las masas de partículas como el bosón de Higgs sean calculables. El problema es en algunos sentidos exclusivo de las partículas de espín 0 (como el bosón de Higgs), lo que puede dar lugar a problemas relacionados con correcciones cuánticas que no afectan a las partículas con espín. [157] Se han propuesto varias soluciones , incluidas la supersimetría , soluciones conformes y soluciones a través de dimensiones adicionales, como los modelos de braneworld .
También existen cuestiones de trivialidad cuántica , lo que sugiere que puede no ser posible crear una teoría de campo cuántico consistente que involucre partículas escalares elementales. [159] Las restricciones de trivialidad se pueden utilizar para restringir o predecir parámetros como la masa del bosón de Higgs. Esto también puede conducir a una masa de Higgs predecible en escenarios de seguridad asintótica .
En el Modelo Estándar, el campo de Higgs es un campo taquiónico escalar – escalar significa que no se transforma bajo las transformaciones de Lorentz , y taquiónico significa que el campo (pero no la partícula) tiene masa imaginaria , y en ciertas configuraciones debe sufrir una ruptura de simetría . Consta de cuatro componentes: dos campos neutros y dos campos de componentes cargados . Ambos componentes cargados y uno de los campos neutros son bosones de Goldstone , que actúan como los componentes de tercera polarización longitudinal de los bosones masivos W + , W − y Z. El cuanto del componente neutro restante corresponde a (y se realiza teóricamente como) el bosón de Higgs masivo. [160] Este componente puede interactuar con los fermiones a través del acoplamiento de Yukawa para darles masa también.
Matemáticamente, el campo de Higgs tiene masa imaginaria y, por lo tanto, es un campo taquiónico . [v] Si bien los taquiones ( partículas que se mueven más rápido que la luz ) son un concepto puramente hipotético, los campos con masa imaginaria han llegado a desempeñar un papel importante en la física moderna. [162] [163] Bajo ninguna circunstancia las excitaciones se propagan más rápido que la luz en tales teorías: la presencia o ausencia de una masa taquiónica no tiene ningún efecto sobre la velocidad máxima de las señales (no hay violación de la causalidad ). [164] En lugar de partículas más rápidas que la luz, la masa imaginaria crea una inestabilidad: cualquier configuración en la que una o más excitaciones de campo sean taquiónicas debe decaer espontáneamente, y la configuración resultante no contiene taquiones físicos. Este proceso se conoce como condensación de taquiones y ahora se cree que es la explicación de cómo surge el mecanismo de Higgs en la naturaleza y, por lo tanto, la razón detrás de la ruptura de la simetría electrodébil.
Aunque la noción de masa imaginaria puede parecer inquietante, es sólo el campo, y no la masa en sí, lo que está cuantizado. Por lo tanto, los operadores de campo en puntos separados espacialmente todavía conmutan (o anticonmutan) , y la información y las partículas todavía no se propagan más rápido que la luz. [165] La condensación de taquiones lleva a un sistema físico que ha alcanzado un límite local –y del que se podría esperar ingenuamente que produzca taquiones físicos– a un estado estable alternativo donde no existen taquiones físicos. Una vez que un campo taquiónico como el campo de Higgs alcanza el mínimo del potencial, sus cuantos ya no son taquiones sino partículas ordinarias como el bosón de Higgs. [166]
Como el campo de Higgs es escalar , el bosón de Higgs no tiene espín . El bosón de Higgs también es su propia antipartícula , es CP-par y tiene carga eléctrica y de color cero . [167]
El Modelo Estándar no predice la masa del bosón de Higgs. [168] Si esa masa está entre115 y 180 GeV/ c 2 (consistente con observaciones empíricas de125 GeV/ c 2 ), entonces el Modelo Estándar puede ser válido en escalas de energía hasta la escala de Planck (10 19 GeV/ c 2 ). [169] Debería ser la única partícula en el Modelo Estándar que sigue siendo masiva incluso a altas energías. Muchos teóricos esperan que surja nueva física más allá del Modelo Estándar en la escala de TeV, basándose en propiedades insatisfactorias del Modelo Estándar. [170] La escala de masa más alta posible permitida para el bosón de Higgs (o algún otro mecanismo de ruptura de simetría electrodébil) es 1,4 TeV; más allá de este punto, el Modelo Estándar se vuelve inconsistente sin tal mecanismo, porque la unitaridad se viola en ciertos procesos de dispersión. [171]
También es posible, aunque experimentalmente difícil, estimar la masa del bosón de Higgs indirectamente: en el Modelo Estándar, el bosón de Higgs tiene una serie de efectos indirectos; en particular, los bucles de Higgs dan lugar a pequeñas correcciones en las masas de los bosones W y Z. Las mediciones precisas de parámetros electrodébiles, como la constante de Fermi y las masas de los bosones W y Z, se pueden utilizar para calcular las restricciones sobre la masa del bosón de Higgs. A partir de julio de 2011, las mediciones precisas electrodébiles nos indican que es probable que la masa del bosón de Higgs sea inferior a aproximadamente161 GeV/ c 2 con un nivel de confianza del 95 % . [w] Estas restricciones indirectas se basan en el supuesto de que el Modelo Estándar es correcto. Todavía puede ser posible descubrir un bosón de Higgs por encima de estas masas, si está acompañado por otras partículas además de las que admite el Modelo Estándar. [173]
El LHC no puede medir directamente la vida del bosón de Higgs debido a su extrema brevedad. Se predice que1,56 × 10 −22 s basado en el ancho de desintegración previsto de4,07 × 10 −3 GeV . [2] Sin embargo, se puede medir indirectamente, basándose en la comparación de masas medidas a partir de fenómenos cuánticos que ocurren en las vías de producción dentro de la capa y en las vías de producción fuera de la capa , mucho más raras , derivadas de la desintegración de Dalitz a través de un fotón virtual (H → γ*γ → ℓℓγ) . Usando esta técnica, la vida útil del bosón de Higgs se midió tentativamente en 2021 como 1,2 –4,6 × 10 −22 s , con una significancia de sigma 3,2 (1 en 1000). [3] [4]
Si las teorías de partículas de Higgs son válidas, entonces una partícula de Higgs puede producirse de manera muy similar a otras partículas que se estudian, en un colisionador de partículas . Esto implica acelerar una gran cantidad de partículas a energías extremadamente altas y extremadamente cercanas a la velocidad de la luz , y luego permitir que choquen entre sí. Los protones y los iones de plomo (los núcleos desnudos de los átomos de plomo ) se utilizan en el LHC. En las energías extremas de estas colisiones, ocasionalmente se producirán las partículas esotéricas deseadas y esto puede detectarse y estudiarse; cualquier ausencia o diferencia con respecto a las expectativas teóricas también puede usarse para mejorar la teoría. La teoría de partículas relevante (en este caso, el Modelo Estándar) determinará los tipos necesarios de colisiones y detectores. El Modelo Estándar predice que los bosones de Higgs podrían formarse de varias maneras, [94] [174] [175] aunque siempre se espera que la probabilidad de producir un bosón de Higgs en cualquier colisión sea muy pequeña; por ejemplo, solo un bosón de Higgs por cada 10 mil millones de colisiones en el Gran Colisionador de Hadrones. [q] Los procesos esperados más comunes para la producción del bosón de Higgs son:

La mecánica cuántica predice que si es posible que una partícula se descomponga en un conjunto de partículas más ligeras, entonces eventualmente lo hará. [176] Esto también es cierto para el bosón de Higgs. La probabilidad con la que esto sucede depende de una variedad de factores que incluyen: la diferencia de masa, la fuerza de las interacciones, etc. La mayoría de estos factores están fijados por el Modelo Estándar, excepto la masa del propio bosón de Higgs. Para un bosón de Higgs con una masa de125 GeV/ c 2 el SM predice una vida media de aproximadamente1,6 × 10 −22 s . [b]
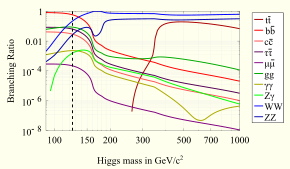
Dado que interactúa con todas las partículas elementales masivas del SM, el bosón de Higgs puede desintegrarse mediante muchos procesos diferentes. Cada uno de estos procesos posibles tiene su propia probabilidad, expresada como la razón de ramificación ; la fracción del número total de desintegraciones que sigue a ese proceso. El SM predice estas razones de ramificación como una función de la masa del bosón de Higgs (ver gráfico).
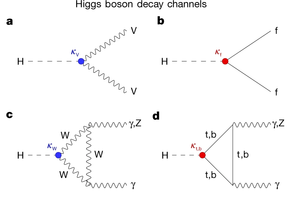
Una forma en que el Higgs puede desintegrarse es dividiéndose en un par fermión-antifermión. Como regla general, es más probable que el Higgs se desintegra en fermiones pesados que en fermiones ligeros, porque la masa de un fermión es proporcional a la fuerza de su interacción con el Higgs. [126] Según esta lógica, la desintegración más común debería ser en un par quark top -antitop. Sin embargo, tal desintegración solo sería posible si el Higgs fuera más pesado que ~346 GeV/ c 2 , el doble de la masa del quark top. Para una masa de Higgs de125 GeV/ c 2 el SM predice que la desintegración más común es en un par quark bottom -antibottom, lo que ocurre el 57,7% del tiempo. [2] La segunda desintegración más común de fermiones a esa masa es un par tau -antitau, que ocurre solo alrededor del 6,3% del tiempo. [2]
Otra posibilidad es que el Higgs se divida en un par de bosones gauge masivos. La posibilidad más probable es que el Higgs se desintegre en un par de bosones W (la línea azul claro en el gráfico), lo que sucede aproximadamente el 21,5 % de las veces para un bosón de Higgs con una masa de125 GeV/ c 2 . [2] Los bosones W pueden desintegrarse posteriormente en un quark y un antiquark o en un leptón cargado y un neutrino. Las desintegraciones de los bosones W en quarks son difíciles de distinguir del fondo, y las desintegraciones en leptones no pueden reconstruirse por completo (porque los neutrinos son imposibles de detectar en experimentos de colisión de partículas). Una señal más clara la proporciona la desintegración en un par de bosones Z (lo que ocurre aproximadamente el 2,6 % del tiempo para un bosón de Higgs con una masa de125 GeV/ c 2 ), [2] si cada uno de los bosones se desintegra posteriormente en un par de leptones cargados fáciles de detectar ( electrones o muones ).
La desintegración en bosones gauge sin masa (es decir, gluones o fotones ) también es posible, pero requiere un bucle intermedio de quarks pesados virtuales (superiores o inferiores) o bosones gauge masivos. [126] El proceso más común de este tipo es la desintegración en un par de gluones a través de un bucle de quarks pesados virtuales. Este proceso, que es el inverso del proceso de fusión de gluones mencionado anteriormente, ocurre aproximadamente el 8,6 % del tiempo para un bosón de Higgs con una masa de125 GeV/ c 2 . [2] Mucho más rara es la desintegración en un par de fotones mediada por un bucle de bosones W o quarks pesados, que ocurre solo dos veces por cada mil desintegraciones. [2] Sin embargo, este proceso es muy relevante para las búsquedas experimentales del bosón de Higgs, porque la energía y el momento de los fotones se pueden medir con mucha precisión, lo que da una reconstrucción precisa de la masa de la partícula en desintegración. [126]
En 2021 se observó tentativamente la extremadamente rara desintegración de Dalitz, [ cita requerida ] en dos leptones (electrones o muones) y un fotón (ℓℓγ), a través de la desintegración de un fotón virtual . Esto puede suceder de tres maneras: de Higgs a fotón virtual a ℓℓγ en el que el fotón virtual (γ*) tiene una masa muy pequeña pero distinta de cero, de Higgs a bosón Z a ℓℓγ, o de Higgs a dos leptones, uno de los cuales emite un fotón de estado final que conduce a ℓℓγ. ATLAS buscó evidencia de la primera de estas (H → γ*γ → ℓℓγ) a baja masa de dileptón (≤30 GeV/ c 2 ) , donde este proceso debería dominar. La observación tiene una significancia de sigma 3,2 (1 en 1000). [3] [4] Esta ruta de desintegración es importante porque facilita la medición de la masa dentro y fuera de la capa del bosón de Higgs (lo que permite la medición indirecta del tiempo de desintegración), y la desintegración en dos partículas cargadas permite la exploración de la conjugación de carga y la violación de la paridad de carga (CP) . [4]
El nombre más fuertemente asociado con la partícula y el campo es el de bosón de Higgs [92] : 168 y campo de Higgs. Durante algún tiempo la partícula fue conocida por una combinación de los nombres de sus autores de PRL (incluyendo a veces a Anderson), por ejemplo, la partícula Brout–Englert–Higgs, la partícula Anderson–Higgs, o el mecanismo Englert–Brout–Higgs–Guralnik–Hagen–Kibble, [x] y estos todavía se usan a veces. [64] [179] Impulsado en parte por la cuestión del reconocimiento y un potencial Premio Nobel compartido, [179] [180] el nombre más apropiado todavía fue ocasionalmente un tema de debate hasta 2013. [179] El propio Higgs prefería llamar a la partícula ya sea por un acrónimo de todos los involucrados, o "el bosón escalar", o "la llamada partícula de Higgs". [180]
Se ha escrito mucho sobre cómo el nombre de Higgs llegó a ser usado exclusivamente. Se ofrecen dos explicaciones principales. La primera es que Higgs emprendió un paso que fue único, más claro o más explícito en su artículo al predecir y examinar formalmente la partícula. De los autores de los artículos de PRL, solo el artículo de Higgs ofreció explícitamente como predicción que existiría una partícula masiva y calculó algunas de sus propiedades; [181] [92] : 167 por lo tanto fue "el primero en postular la existencia de una partícula masiva" según Nature . [179] El físico y autor Frank Close y el físico-bloguero Peter Woit comentan que el artículo de GHK también se completó después de que Higgs y Brout-Englert fueran enviados a Physical Review Letters , [182] [92] : 167 y que Higgs solo había llamado la atención sobre un bosón escalar masivo predicho , mientras que todos los demás se habían centrado en los bosones vectoriales masivos. [182] [92] : 154,166,175 De esta manera, la contribución de Higgs también proporcionó a los experimentalistas un "objetivo concreto" crucial necesario para probar la teoría. [183]
Sin embargo, en opinión de Higgs, Brout y Englert no mencionaron explícitamente el bosón ya que su existencia es claramente obvia en su trabajo, [69] : 6 mientras que según Guralnik el artículo de GHK era un análisis completo de todo el mecanismo de ruptura de simetría cuyo rigor matemático está ausente en los otros dos artículos, y una partícula masiva puede existir en algunas soluciones. [93] : 9 El artículo de Higgs también proporcionó una declaración "especialmente aguda" del desafío y su solución según el historiador de la ciencia David Kaiser. [180]
La explicación alternativa es que el nombre se popularizó en la década de 1970 debido a su uso como abreviatura conveniente o debido a un error en la cita. Muchos relatos ( incluido el propio Higgs [69] : 7 ) atribuyen el nombre "Higgs" al físico Benjamin Lee . [y] Lee fue un divulgador importante de la teoría en sus inicios, y habitualmente adjuntó el nombre "Higgs" como una "abreviatura conveniente" para sus componentes desde 1972, [17] [179] [184] [185] [186] y en al menos una instancia desde 1966. [187] Aunque Lee aclaró en sus notas a pie de página que "'Higgs' es una abreviatura de Higgs, Kibble, Guralnik, Hagen, Brout, Englert", [184] su uso del término (y quizás también la cita errónea de Steven Weinberg del artículo de Higgs como el primero en su artículo seminal de 1967 [92] [188] [187] ) significó que alrededor de 1975-1976 otros también habían comenzado a usar el nombre "Higgs" exclusivamente como una abreviatura. [z] En 2012, el físico Frank Wilczek , a quien se le atribuye el nombre de la partícula elemental, el axión (en lugar de una propuesta alternativa "Higglet", de Weinberg), respaldó el nombre "bosón de Higgs", afirmando que "la historia es complicada, y donde sea que traces la línea, habrá alguien justo debajo de ella". [180]
En los medios populares fuera de la comunidad científica, a menudo se hace referencia al bosón de Higgs como la "partícula de Dios". [189] [190] [191] [192] [193] El apodo proviene del título del libro de 1993 sobre el bosón de Higgs y la física de partículas, La partícula de Dios: si el universo es la respuesta, ¿cuál es la pregunta? del ganador del Premio Nobel de Física y director del Fermilab, Leon Lederman . [28] Lederman lo escribió en el contexto del fracaso del apoyo del gobierno de los EE. UU. al Supercolisionador Superconductor , [194] un competidor titánico parcialmente construido [195] [196] del Gran Colisionador de Hadrones con energías de colisión planificadas de 2 × 20 TeV que fue defendido por Lederman desde su inicio en 1983 [194] [aa] [197] [198] y cerrado en 1993. El libro buscaba en parte promover la conciencia de la importancia y la necesidad de un proyecto de este tipo ante su posible pérdida de financiación. [199] Lederman, un investigador líder en el campo, escribe que quería titular su libro La maldita partícula: si el universo es la respuesta, ¿cuál es la pregunta? El editor de Lederman decidió que el título era demasiado controvertido y lo convenció de cambiarlo a La partícula de Dios: si el universo es la respuesta, ¿cuál es la pregunta? [200]
Aunque el uso de este término por parte de los medios puede haber contribuido a una mayor conciencia e interés, [201] muchos científicos sienten que el nombre es inapropiado [17] [18] [202] ya que es una hipérbole sensacionalista y engaña a los lectores; [203] la partícula tampoco tiene nada que ver con ningún Dios, deja abiertas numerosas preguntas en física fundamental y no explica el origen último del universo . Se informó que Higgs , un ateo , estaba disgustado y declaró en una entrevista de 2008 que lo encontraba "vergonzoso" porque era "el tipo de mal uso [...] que creo que podría ofender a algunas personas". [203] [204] [205] El apodo también ha sido satirizado en los medios de comunicación tradicionales. [206] El escritor científico Ian Sample afirmó en su libro de 2010 sobre la búsqueda que el apodo es "universalmente odiado" por los físicos y quizás el "peor ridiculizado" en la historia de la física , pero que (según Lederman) el editor rechazó todos los títulos que mencionaban "Higgs" por considerarlos poco imaginativos y demasiado desconocidos. [207]
Lederman comienza con una revisión de la larga búsqueda humana de conocimiento, y explica que su título irónico establece una analogía entre el impacto del campo de Higgs en las simetrías fundamentales en el Big Bang , y el aparente caos de estructuras, partículas, fuerzas e interacciones que resultaron y dieron forma a nuestro universo actual, con la historia bíblica de Babel en la que el lenguaje único primordial del Génesis temprano se fragmentó en muchos idiomas y culturas dispares. [208]
Hoy [...] tenemos el modelo estándar, que reduce toda la realidad a una docena de partículas y cuatro fuerzas [...] Es una simplicidad que se ha conseguido con mucho esfuerzo [y] es notablemente precisa. Pero también es incompleta y, de hecho, internamente inconsistente [...] Este bosón es tan central para el estado de la física actual, tan crucial para nuestra comprensión final de la estructura de la materia, y sin embargo tan elusivo, que le he dado un apodo: la Partícula de Dios. ¿Por qué Partícula de Dios? Por dos razones. Una, el editor no nos permitió llamarla la Maldita Partícula, aunque ese podría ser un título más apropiado, dada su naturaleza malvada y el gasto que está causando. Y dos, hay una conexión, de algún modo, con otro libro , uno mucho más antiguo...
- Lederman y Teresi [28] : 22
Lederman pregunta si el bosón de Higgs fue añadido sólo para desconcertar y confundir a quienes buscan el conocimiento del universo, y si los físicos quedarán confundidos por él como se relata en esa historia, o si finalmente superarán el desafío y entenderán "cuán hermoso es el universo que [Dios] ha creado". [209]
En 2009, el periódico británico The Guardian organizó un concurso de cambio de nombre y su corresponsal científico eligió el nombre "bosón de la botella de champán " como la mejor propuesta: "El fondo de una botella de champán tiene la forma del potencial de Higgs y se utiliza a menudo como ilustración en las clases de física. Por lo tanto, no es un nombre vergonzosamente grandioso, es memorable y también tiene alguna conexión con la física". [210] El nombre Higgson también fue sugerido en un artículo de opinión en la publicación en línea del Instituto de Física physicsworld.com . [211]

Ha habido un considerable debate público sobre analogías y explicaciones para la partícula de Higgs y cómo el campo crea masa, [212] [213] incluida la cobertura de intentos explicativos por derecho propio y un concurso en 1993 para la mejor explicación popular por el entonces Ministro de Ciencia del Reino Unido, Sir William Waldegrave [214] y artículos en periódicos de todo el mundo.
Una colaboración educativa que involucra a un físico del LHC y a un educador de profesores de secundaria del CERN sugiere que la dispersión de la luz (responsable del arco iris y del prisma dispersivo ) es una analogía útil para la ruptura de la simetría del campo de Higgs y su efecto causante de masa. [215]
Matt Strassler utiliza los campos eléctricos como analogía: [216]
Algunas partículas interactúan con el campo de Higgs, mientras que otras no. Las partículas que sienten el campo de Higgs actúan como si tuvieran masa. Algo similar ocurre en un campo eléctrico : los objetos cargados son atraídos y los objetos neutros pueden atravesarlo sin verse afectados. Por lo tanto, se puede pensar en la búsqueda del bosón de Higgs como un intento de crear ondas en el campo de Higgs [ crear bosones de Higgs ] para demostrar que realmente está allí.
The Guardian ofreció una explicación similar : [217]
El bosón de Higgs es esencialmente una onda en un campo que se dice surgió en el nacimiento del universo y que abarca el cosmos hasta el día de hoy... Sin embargo, la partícula es crucial: es la prueba irrefutable , la evidencia necesaria para demostrar que la teoría es correcta.
El efecto del campo de Higgs sobre las partículas fue descrito por el físico David Miller como algo similar a una sala llena de trabajadores de un partido político distribuidos uniformemente por toda la habitación: la multitud gravita hacia las personas famosas y las frena, pero no frena a los demás. [ab] También llamó la atención sobre los efectos bien conocidos en la física del estado sólido , donde la masa efectiva de un electrón puede ser mucho mayor de lo habitual en presencia de una red cristalina. [218]
Las analogías basadas en efectos de arrastre , incluyendo analogías de " jarabe " o " melaza ", también son bien conocidas, pero pueden ser algo engañosas ya que pueden entenderse (incorrectamente) como diciendo que el campo de Higgs simplemente resiste el movimiento de algunas partículas pero no el de otras – un simple efecto resistivo también podría entrar en conflicto con la tercera ley de Newton . [220]
El bosón de Higgs se suele malinterpretar como responsable de la masa, en lugar del campo de Higgs, y como relacionado con la mayor parte de la masa del universo. [221] [222] [223]
Antes de finales de 2013 se debatió mucho sobre cómo asignar el crédito si se demostraba la existencia del bosón de Higgs, lo que se hizo más evidente porque se esperaba un premio Nobel y la amplia base de personas que tienen derecho a ser consideradas. Entre ellas se incluyen una serie de teóricos que hicieron posible la teoría del mecanismo de Higgs, los teóricos de los artículos de PRL de 1964 (incluido el propio Higgs), los teóricos que derivaron de ellos una teoría electrodébil funcional y el propio Modelo Estándar, y también los experimentalistas del CERN y otras instituciones que hicieron posible la prueba del campo y el bosón de Higgs en la realidad. El premio Nobel tiene un límite de tres personas para compartirlo, y algunos posibles ganadores ya han sido galardonados por otros trabajos o han fallecido (el premio solo se otorga a personas en vida). Entre los premios existentes para trabajos relacionados con el campo, el bosón o el mecanismo de Higgs se incluyen:
El co-investigador de Englert, Robert Brout, había muerto en 2011 y el Premio Nobel normalmente no se otorga póstumamente . [228]
Además, la revisión de 50 años de Physical Review Letters (2008) reconoció los artículos de ruptura de simetría de PRL de 1964 y el artículo de Weinberg de 1967 Un modelo de leptones (el artículo más citado en física de partículas, hasta 2012) como "cartas históricas". [87]
Tras la observación de una partícula similar al Higgs en julio de 2012, varios medios de comunicación indios informaron sobre la supuesta falta de reconocimiento del mérito del físico indio Satyendra Nath Bose , cuyo trabajo en la década de 1920 dio nombre a la clase de partículas " bosones " [229] [230] (aunque los físicos han descrito la conexión de Bose con el descubrimiento como tenue). [231]

En el Modelo Estándar, el campo de Higgs es un campo escalar de cuatro componentes que forma un doblete complejo de la simetría isospín débil SU(2):
mientras el campo tenga carga + 1/2 bajo la simetría de hipercarga débil U(1). [232]
Nota: Este artículo utiliza la convención de escala donde la carga eléctrica, Q , el isospín débil , T 3 , y la hipercarga débil, Y W , están relacionadas por Q = T 3 + Y W . Una convención diferente utilizada en la mayoría de los otros artículos de Wikipedia es Q = T 3 + 1/2 Y W. [233] [234] [235 ]
La parte de Higgs del Lagrangiano es [232]
donde y son los bosones de calibre de las simetrías SU(2) y U(1), y sus respectivas constantes de acoplamiento , son las matrices de Pauli (un conjunto completo de generadores de la simetría SU(2)), y y , de modo que el estado fundamental rompe la simetría SU(2) (véase la figura).
El estado fundamental del campo de Higgs (la parte inferior del potencial) está degenerado con diferentes estados fundamentales relacionados entre sí por una transformación de calibre SU(2). Siempre es posible elegir un calibre tal que en el estado fundamental . El valor esperado de en el estado fundamental (el valor esperado de vacío o VEV) es entonces , donde . El valor medido de este parámetro es ~246 GeV/ c 2 . [126] Tiene unidades de masa y es el único parámetro libre del Modelo Estándar que no es un número adimensional. En y surgen términos cuadráticos que dan masas a los bosones W y Z: [232]
con su relación determinando el ángulo de Weinberg , , y dejando un fotón U(1) sin masa , . La masa del bosón de Higgs en sí está dada por
Los quarks y los leptones interactúan con el campo de Higgs a través de los términos de interacción de Yukawa :
donde son quarks y leptones levógiros y dextrógiros de la i- ésima generación , son matrices de acoplamientos de Yukawa donde hc denota el conjugado hermítico de todos los términos precedentes. En el estado fundamental de ruptura de simetría, sólo permanecen los términos que contienen, dando lugar a términos de masa para los fermiones. Al rotar los campos de quarks y leptones a la base donde las matrices de acoplamientos de Yukawa son diagonales, se obtiene
donde las masas de los fermiones son , y denotan los valores propios de las matrices de Yukawa. [232]
Bernstein (1974) contiene una revisión y antecedentes accesibles y completos de esta área, consulte los enlaces externos.La condición de "calibrador de radiación" ∇⋅A( x ) = 0 claramente no es covariante, lo que significa que si deseamos mantener la transversalidad del fotón en todos los sistemas de Lorentz, el campo de fotones A μ ( x ) no puede transformarse como un cuatrivector . Esto no es una catástrofe, ya que el campo de fotones no es un observable , y uno puede demostrar fácilmente que los elementos de la matriz S, que son observables, tienen estructuras covariantes. ... en las teorías de calibración uno podría disponer las cosas de modo que tuviera una ruptura de simetría debido a la no invariancia del vacío; pero, debido a que la prueba de Goldstone et al. falla, los mesones de Goldstone de masa cero no necesitan aparecer. [ énfasis en el original ]
[P] ¿Por qué los físicos de partículas se preocupan tanto por la partícula de Higgs?
[A] Bueno, en realidad no les importa. Lo que realmente les importa es el campo de Higgs , porque es muy importante. [énfasis en el original]
El campo de Higgs: tan importante que merecía una instalación experimental completa, el Gran Colisionador de Hadrones, dedicada a comprenderlo.
En términos que suelen reservarse para los logros deportivos, los informes de prensa describieron el hallazgo como un hito monumental en la historia de la ciencia.
Incluso en los círculos más especializados, la nueva partícula descubierta en julio aún no se llama «bosón de Higgs». Los físicos aún dudan en llamarlo así antes de haber determinado que sus propiedades encajan con las que la teoría de Higgs predice que tiene el bosón de Higgs.
"Nunca hemos visto una partícula elemental con espín cero", afirmó Tony Weidberg, físico de partículas de la Universidad de Oxford que también participa en los experimentos del CERN.
Es probable que la Tierra desaparezca mucho antes de que las partículas del bosón de Higgs desencadenen un ataque apocalíptico contra el universo
[L]a mala noticia es que su masa sugiere que el universo terminará en una burbuja de catástrofe que se propagará rápidamente. ¿La buena noticia? Probablemente serán decenas de miles de millones de años.El artículo cita a Joseph Lykken, del Fermilab : "Los parámetros de nuestro universo, incluyendo el bosón de Higgs [y las masas del quark top] sugieren que estamos justo al borde de la estabilidad, en un estado "metaestable". Los físicos han estado contemplando esa posibilidad durante más de 30 años. En 1982, los físicos Michael Turner y Frank Wilczek escribieron en Nature que "sin previo aviso, una burbuja de vacío verdadero podría nuclearse en algún lugar del universo y desplazarse hacia afuera..."
[L]a influencia del Higgs (o la influencia de algo parecido) podría llegar mucho más lejos. Por ejemplo, algo como el Higgs, si no exactamente el Higgs en sí, también puede estar detrás de muchas otras "simetrías rotas" inexplicadas en el universo ... De hecho, algo muy parecido al Higgs puede haber estado detrás del colapso de la simetría que llevó al Big Bang, que creó el universo. Cuando las fuerzas comenzaron a separarse de su igualdad primordial, adoptando los caracteres distintivos que tienen hoy, liberaron energía de la misma manera que el agua libera energía cuando se convierte en hielo. Excepto que en este caso, la congelación acumuló suficiente energía para hacer estallar el universo. ... Sea como fuere, la moraleja es clara: sólo cuando la perfección se hace añicos puede nacer todo lo demás.
Gilbert ... escribió una respuesta al artículo [de Klein y Lee] diciendo 'No, no se puede hacer eso en una teoría relativista. No se puede tener un vector de tiempo unitario preferido como ese'. Aquí es donde entré yo, porque el mes siguiente fue cuando respondí al artículo de Gilbert diciendo 'Sí, se puede tener tal cosa', pero solo en una teoría de calibre con un campo de calibre acoplado a la corriente.
Sidney Coleman publicó en la revista Science en 1979 una búsqueda de citas que hizo documentando que esencialmente nadie prestó atención al artículo ganador del Premio Nobel de Weinberg hasta el trabajo de 't Hooft (como lo explicó Ben Lee). En 1971, el interés en el artículo de Weinberg explotó. Tuve una experiencia personal paralela: tomé un curso de un año sobre interacciones débiles con Shelly Glashow en 1970, y nunca mencionó el modelo de Weinberg-Salam o sus propias contribuciones.
[Una] colaboración global de más de 170 centros de computación en 36 países... para almacenar, distribuir y analizar los ~25 Petabytes (25 millones de Gigabytes) de datos generados anualmente por el Gran Colisionador de Hadrones
Ahora conecta miles de computadoras y sistemas de almacenamiento en más de 170 centros en 41 países. ... El WLCG es la red informática más grande del mundo
{{cite arXiv}}: CS1 maint: numeric names: authors list (link)La significación estadística no es lo suficientemente grande como para decir algo concluyente. A día de hoy, lo que vemos es consistente con una fluctuación de fondo o con la presencia del bosón. Los análisis refinados y los datos adicionales entregados en 2012 por esta magnífica máquina definitivamente darán una respuesta.
Por primera vez, los científicos han podido analizar la dinámica de las redes sociales a escala global antes, durante y después del anuncio de un importante descubrimiento científico.
Rolf Heuer, director del [CERN], dijo que confía en que "hacia mediados de año, estaremos allí".
– Entrevista de AP, en el Foro Económico Mundial, 26 de enero de 2013.
'Tendrán que pasar algunos años más' después de que se reinicie el colisionador para confirmar definitivamente que la partícula recién descubierta es el bosón de Higgs.
citando la presentación de Lee en ICHEP 1972 en Fermilab: "... que se conoce como el mecanismo de Higgs..." y "la locución de Lee", su explicación a pie de página de esta abreviatura.
Lee ... aparentemente utilizó el término 'bosón de Higgs' ya en 1966 ... pero lo que puede haber hecho que el término se mantenga es un artículo seminal de Steven Weinberg ... publicado en 1967 ... Weinberg reconoció la confusión en un ensayo en la
New York Review of Books
en mayo de 2012.
(Véase también el artículo original en
El SSC, propuesto por el Departamento de Energía de Estados Unidos en 1983, es un proyecto alucinante... este gigantesco laboratorio... este proyecto titánico
... este complejo titánico...
Lederman, que se considera un propagandista no oficial del supercolisionador, dijo que el SSC podría revertir la fuga de cerebros en física en la que jóvenes físicos brillantes han dejado Estados Unidos para trabajar en Europa y otros lugares.
fue un experimentador de alta energía consumado que había hecho contribuciones ganadoras del Premio Nobel al desarrollo del Modelo Estándar durante la década de 1960 (aunque el premio en sí no llegó hasta 1988). Fue un elemento fijo en las audiencias del Congreso sobre el colisionador, un defensor desenfrenado de sus méritos.
La posibilidad de que la próxima gran máquina creara el bosón de Higgs se convirtió en una zanahoria para colgar frente a las agencias de financiación y los políticos. Un destacado físico estadounidense, Leon Lederman [sic], promocionó el bosón de Higgs como la partícula de Dios en el título de un libro publicado en 1993 [...] Lederman participó en una campaña para persuadir al gobierno de los EE. UU. de que continuara financiando el Supercolisionador Superconductor [...] la tinta no se había secado en el libro de Lederman antes de que el Congreso de los EE. UU. decidiera cancelar los miles de millones de dólares ya gastados
Consideremos el universo primitivo: un estado de pura y perfecta nada; una niebla informe de materia indiferenciada
[...] 'simetría perfecta'
[...] ¿Qué destrozó esta perfección primordial? Un posible culpable es el llamado campo de Higgs
[...] El físico Leon Lederman compara la forma en que opera el Higgs con la historia bíblica de Babel [cuyos ciudadanos] hablaban todos el mismo idioma
[...] Como Dios, dice Lederman, el Higgs diferenciaba la igualdad perfecta, confundiendo a todos (físicos incluidos)
[...] [El premio Nobel Richard]
Feynman
se preguntó por qué el universo en el que vivimos estaba tan obviamente torcido
[...] Tal vez, especuló, la perfección total habría sido inaceptable para Dios. Y así, tal como Dios rompió la perfección de Babel, "Dios hizo que las leyes fueran sólo casi simétricas".
{{cite web}}: CS1 maint: unfit URL (link)