Transformación de Lorentz

Familia de transformaciones lineales

En física , las transformaciones de Lorentz son una familia de seis parámetros de transformaciones lineales desde un sistema de coordenadas en el espacio-tiempo a otro sistema que se mueve a una velocidad constante con respecto al primero. La transformación inversa respectiva se parametriza entonces por el negativo de esta velocidad. Las transformaciones reciben su nombre del físico holandés Hendrik Lorentz .

La forma más común de la transformación, parametrizada por la constante real que representa una velocidad confinada a la dirección x , se expresa como ^{[1] [2]} donde ( t , x , y , z ) y ( t ′, x ′, y ′, z ′) son las coordenadas de un evento en dos marcos con los orígenes espaciales coincidiendo en t = t ′ = 0, donde el marco primado se ve desde el marco no primado como moviéndose con velocidad v a lo largo del eje x , donde c es la velocidad de la luz , y es el factor de Lorentz . Cuando la velocidad v es mucho menor que c , el factor de Lorentz es despreciablemente diferente de 1, pero a medida que v se acerca a c , crece sin límite. El valor de v debe ser menor que c para que la transformación tenga sentido. ${\displaystyle v,}$ $${\displaystyle {\begin{aligned}t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\x'&=\gamma \left(x-vt\right)\\y'&=y\\z'&=z\end{aligned}}}$$ ${\textstyle \gamma =\left({\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\right)^{-1}}$ ${\displaystyle \gamma }$

Expresar la velocidad como una forma equivalente de la transformación es ^[3] ${\textstyle \beta ={\frac {v}{c}},}$ $${\displaystyle {\begin{aligned}ct'&=\gamma \left(ct-\beta x\right)\\x'&=\gamma \left(x-\beta ct\right)\\y'&=y\\z'&=z.\end{aligned}}}$$

Los sistemas de referencia se pueden dividir en dos grupos: inerciales (movimiento relativo con velocidad constante) y no inerciales (aceleración, movimiento en trayectorias curvas, movimiento rotacional con velocidad angular constante , etc.). El término "transformaciones de Lorentz" se refiere únicamente a las transformaciones entre sistemas inerciales , generalmente en el contexto de la relatividad especial.

En cada marco de referencia , un observador puede utilizar un sistema de coordenadas local (normalmente coordenadas cartesianas en este contexto) para medir longitudes, y un reloj para medir intervalos de tiempo. Un acontecimiento es algo que sucede en un punto del espacio en un instante de tiempo, o más formalmente un punto del espacio-tiempo . Las transformaciones conectan las coordenadas espaciales y temporales de un acontecimiento medido por un observador en cada marco. ^{[nb 1]}

Reemplazan la transformación galileana de la física newtoniana , que supone un espacio y un tiempo absolutos (véase la relatividad galileana ). La transformación galileana es una buena aproximación solo a velocidades relativas mucho menores que la velocidad de la luz. Las transformaciones de Lorentz tienen una serie de características poco intuitivas que no aparecen en las transformaciones galileanas. Por ejemplo, reflejan el hecho de que los observadores que se mueven a diferentes velocidades pueden medir diferentes distancias , tiempos transcurridos e incluso diferentes ordenaciones de eventos , pero siempre de manera que la velocidad de la luz sea la misma en todos los marcos de referencia inerciales. La invariancia de la velocidad de la luz es uno de los postulados de la relatividad especial .

Históricamente, las transformaciones fueron el resultado de los intentos de Lorentz y otros de explicar cómo se observaba que la velocidad de la luz era independiente del marco de referencia y de comprender las simetrías de las leyes del electromagnetismo . Las transformaciones se convirtieron más tarde en una piedra angular de la relatividad especial .

La transformación de Lorentz es una transformación lineal . Puede incluir una rotación del espacio; una transformación de Lorentz sin rotación se denomina impulso de Lorentz . En el espacio de Minkowski (el modelo matemático del espacio-tiempo en la relatividad especial), las transformaciones de Lorentz preservan el intervalo de espacio-tiempo entre dos eventos cualesquiera. Esta propiedad es la propiedad definitoria de una transformación de Lorentz. Describen solo las transformaciones en las que el evento del espacio-tiempo en el origen se deja fijo. Pueden considerarse como una rotación hiperbólica del espacio de Minkowski. El conjunto más general de transformaciones que también incluye traslaciones se conoce como el grupo de Poincaré .

Historia

Muchos físicos, incluidos Woldemar Voigt , George FitzGerald , Joseph Larmor y el propio Hendrik Lorentz ^[4] , habían estado discutiendo la física implícita en estas ecuaciones desde 1887. ^[5] A principios de 1889, Oliver Heaviside había demostrado a partir de las ecuaciones de Maxwell que el campo eléctrico que rodea una distribución esférica de carga debería dejar de tener simetría esférica una vez que la carga está en movimiento en relación con el éter luminífero . FitzGerald luego conjeturó que el resultado de distorsión de Heaviside podría aplicarse a una teoría de fuerzas intermoleculares. Algunos meses después, FitzGerald publicó la conjetura de que los cuerpos en movimiento se contraen, para explicar el desconcertante resultado del experimento de éter-viento de 1887 de Michelson y Morley . En 1892, Lorentz presentó de forma independiente la misma idea de una manera más detallada, que posteriormente se denominó hipótesis de contracción de FitzGerald-Lorentz . ^[6] Su explicación era ampliamente conocida antes de 1905. ^[7]

Lorentz (1892-1904) y Larmor (1897-1900), que creían en la hipótesis del éter luminífero, también buscaron la transformación bajo la cual las ecuaciones de Maxwell son invariantes cuando se transforman del éter a un marco móvil. Extendieron la hipótesis de contracción de FitzGerald-Lorentz y descubrieron que la coordenada temporal también debe modificarse (" tiempo local "). Henri Poincaré dio una interpretación física del tiempo local (de primer orden en v / c , la velocidad relativa de los dos marcos de referencia normalizada a la velocidad de la luz) como consecuencia de la sincronización del reloj, bajo el supuesto de que la velocidad de la luz es constante en marcos móviles. ^[8] Se atribuye a Larmor haber sido el primero en comprender la crucial propiedad de dilatación del tiempo inherente a sus ecuaciones. ^[9]

En 1905, Poincaré fue el primero en reconocer que la transformación tiene las propiedades de un grupo matemático , y la nombró en honor a Lorentz. ^[10] Más tarde, ese mismo año, Albert Einstein publicó lo que ahora se llama relatividad especial , al derivar la transformación de Lorentz bajo los supuestos del principio de relatividad y la constancia de la velocidad de la luz en cualquier marco de referencia inercial , y al abandonar el éter mecanicista por innecesario. ^[11]

Derivación del grupo de transformaciones de Lorentz

Un evento es algo que sucede en un punto determinado del espacio-tiempo o, de manera más general, en el punto mismo del espacio-tiempo. En cualquier sistema inercial, un evento se especifica mediante una coordenada temporal ct y un conjunto de coordenadas cartesianas x , y , z para especificar la posición en el espacio en ese sistema. Los subíndices etiquetan eventos individuales.

Del segundo postulado de la relatividad de Einstein (invariancia de c ) se deduce que:

en todos los sistemas inerciales para eventos conectados por señales luminosas . La cantidad de la izquierda se llama intervalo espacio-temporal entre los eventos a ₁ = ( t ₁ , x ₁ , y ₁ , z ₁ ) y a ₂ = ( t ₂ , x ₂ , y ₂ , z ₂ ) . El intervalo entre dos eventos cualesquiera , no necesariamente separados por señales luminosas, es de hecho invariante, es decir, independiente del estado de movimiento relativo de los observadores en diferentes sistemas inerciales, como se muestra utilizando la homogeneidad y la isotropía del espacio . La transformación buscada debe poseer, por tanto, la propiedad de que:

donde ( t , x , y , z ) son las coordenadas espacio-temporales utilizadas para definir eventos en un marco, y ( t ′, x ′, y ′, z ′) son las coordenadas en otro marco. Primero se observa que ( D2 ) se satisface si se agrega una 4 -tupla arbitraria b de números a los eventos a ₁ y a ₂ . Tales transformaciones se denominan traslaciones espacio-temporales y no se tratan más aquí. Luego se observa que una solución lineal que preserva el origen del problema más simple resuelve también el problema general:

(una solución que satisface la primera fórmula satisface automáticamente también la segunda; ver identidad de polarización ). Encontrar la solución al problema más simple es solo cuestión de buscar en la teoría de grupos clásicos que preservan formas bilineales de varias firmas. ^{[nb 2]} La primera ecuación en ( D3 ) se puede escribir de manera más compacta como:

donde (·, ·) se refiere a la forma bilineal de la signatura (1, 3) en R ⁴ expuesta por la fórmula del lado derecho en ( D3 ). La notación alternativa definida a la derecha se conoce como el producto escalar relativista . El espacio-tiempo visto matemáticamente como R ⁴ dotado de esta forma bilineal se conoce como espacio de Minkowski M . La transformación de Lorentz es, por tanto, un elemento del grupo O(1, 3) , el grupo de Lorentz o, para aquellos que prefieren la otra signatura métrica , O(3, 1) (también llamado el grupo de Lorentz). ^{[nb 3]} Se tiene:

que es precisamente la conservación de la forma bilineal ( D3 ) lo que implica (por linealidad de Λ y bilinealidad de la forma) que ( D2 ) se satisface. Los elementos del grupo de Lorentz son rotaciones y empujes y mezclas de los mismos. Si se incluyen las traslaciones espaciotemporales, entonces se obtiene el grupo de Lorentz no homogéneo o el grupo de Poincaré .

Generalidades

Las relaciones entre las coordenadas espacio-temporales primitivas y no primitivas son las transformaciones de Lorentz ; cada coordenada en un sistema es una función lineal de todas las coordenadas en el otro sistema, y ​​las funciones inversas son la transformación inversa. Dependiendo de cómo se mueven los sistemas entre sí y de cómo están orientados en el espacio entre sí, otros parámetros que describen la dirección, la velocidad y la orientación entran en las ecuaciones de transformación.

Las transformaciones que describen el movimiento relativo con velocidad constante (uniforme) y sin rotación de los ejes de coordenadas espaciales se denominan boosts de Lorentz o simplemente boosts , y la velocidad relativa entre los marcos es el parámetro de la transformación. El otro tipo básico de transformación de Lorentz es la rotación solo en las coordenadas espaciales, estas como boosts son transformaciones inerciales ya que no hay movimiento relativo, los marcos simplemente están inclinados (y no rotan continuamente), y en este caso las cantidades que definen la rotación son los parámetros de la transformación (por ejemplo, representación eje-ángulo , o ángulos de Euler , etc.). Una combinación de rotación e boost es una transformación homogénea , que transforma el origen de nuevo al origen.

El grupo de Lorentz completo O(3, 1) también contiene transformaciones especiales que no son ni rotaciones ni impulsos, sino más bien reflexiones en un plano que pasa por el origen. Se pueden distinguir dos de ellas: la inversión espacial , en la que se invierte el signo de las coordenadas espaciales de todos los eventos, y la inversión temporal, en la que se invierte el signo de la coordenada temporal de cada evento.

Los impulsos no deben confundirse con meros desplazamientos en el espacio-tiempo; en este caso, los sistemas de coordenadas simplemente se desplazan y no hay movimiento relativo. Sin embargo, también cuentan como simetrías forzadas por la relatividad especial, ya que dejan invariable el intervalo espacio-tiempo. Una combinación de una rotación con un impulso, seguida de un desplazamiento en el espacio-tiempo, es una transformación de Lorentz no homogénea , un elemento del grupo de Poincaré, que también se denomina grupo de Lorentz no homogéneo.

Formulación física de los impulsos de Lorentz

Transformación de coordenadas

Las coordenadas espacio-temporales de un evento, medidas por cada observador en su sistema de referencia inercial (en configuración estándar), se muestran en los globos de diálogo.
Arriba: el sistema F ′ se mueve a una velocidad v a lo largo del eje x del sistema F .
Abajo: el sistema F se mueve a una velocidad − v a lo largo del eje x ′ del sistema F ′ . ^[12]

Un observador "estacionario" en el marco F define eventos con coordenadas t , x , y , z . Otro marco F ′ se mueve con velocidad v relativa a F , y un observador en este marco "móvil" F ′ define eventos utilizando las coordenadas t ′, x ′, y ′, z ′ .

Los ejes de coordenadas en cada marco son paralelos (los ejes x y x ′ son paralelos, los ejes y e y ′ son paralelos, y los ejes z y z ′ son paralelos ), permanecen mutuamente perpendiculares, y el movimiento relativo es a lo largo de los ejes xx′ coincidentes . En t = t ′ = 0 , los orígenes de ambos sistemas de coordenadas son los mismos, ( x, y, z ) = ( x ′, y ′, z ′) = (0, 0, 0) . En otras palabras, los tiempos y las posiciones son coincidentes en este evento. Si todo esto se cumple, entonces se dice que los sistemas de coordenadas están en configuración estándar o sincronizados .

Si un observador en F registra un evento t , x , y , z , entonces un observador en F ′ registra el mismo evento con coordenadas ^[13]

Impulso de Lorentz ( dirección x )

${\displaystyle {\begin{aligned}t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\x'&=\gamma \left(x-vt\right)\\y'&=y\\z'&=z\end{aligned}}}$

donde v es la velocidad relativa entre fotogramas en la dirección x , c es la velocidad de la luz y ( gamma minúscula ) es el factor de Lorentz . $${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$$

Aquí, v es el parámetro de la transformación, para un impulso dado es un número constante, pero puede tomar un rango continuo de valores. En la configuración utilizada aquí, la velocidad relativa positiva v > 0 es movimiento a lo largo de las direcciones positivas de los ejes xx ′ , la velocidad relativa cero v = 0 es ningún movimiento relativo, mientras que la velocidad relativa negativa v < 0 es movimiento relativo a lo largo de las direcciones negativas de los ejes xx ′ . La magnitud de la velocidad relativa v no puede ser igual o mayor que c , por lo que solo se permiten velocidades subluminales − c < v < c . El rango correspondiente de γ es 1 ≤ γ < ∞ .

Las transformaciones no están definidas si v está fuera de estos límites. A la velocidad de la luz ( v = c ) γ es infinito, y más rápido que la luz ( v > c ) γ es un número complejo , cada uno de los cuales hace que las transformaciones no sean físicas. Las coordenadas de espacio y tiempo son cantidades mensurables y numéricamente deben ser números reales.

Como transformación activa , un observador en F′ nota que las coordenadas del evento se "impulsan" en las direcciones negativas de los ejes xx ′ , debido a la − v en las transformaciones. Esto tiene el efecto equivalente del sistema de coordenadas F′ impulsado en las direcciones positivas de los ejes xx ′ , mientras que el evento no cambia y simplemente se representa en otro sistema de coordenadas, una transformación pasiva .

Las relaciones inversas ( t , x , y , z en términos de t ′, x ′, y ′, z ′ ) se pueden encontrar resolviendo algebraicamente el conjunto original de ecuaciones. Una forma más eficiente es usar principios físicos. Aquí F ′ es el marco "estacionario" mientras que F es el marco "móvil". De acuerdo con el principio de relatividad, no hay un marco de referencia privilegiado, por lo que las transformaciones de F ′ a F deben tomar exactamente la misma forma que las transformaciones de F a F ′ . La única diferencia es que F se mueve con velocidad − v relativa a F ′ (es decir, la velocidad relativa tiene la misma magnitud pero está dirigida en sentido opuesto). Por lo tanto, si un observador en F ′ nota un evento t ′, x ′, y ′, z ′ , entonces un observador en F nota el mismo evento con coordenadas

Impulso de Lorentz inverso ( dirección x )

${\displaystyle {\begin{aligned}t&=\gamma \left(t'+{\frac {vx'}{c^{2}}}\right)\\x&=\gamma \left(x'+vt'\right)\\y&=y'\\z&=z',\end{aligned}}}$

y el valor de γ permanece invariable. Este "truco" de simplemente invertir la dirección de la velocidad relativa mientras se conserva su magnitud, e intercambiar las variables cebadas y no cebadas, siempre se aplica para encontrar la transformación inversa de cada impulso en cualquier dirección.

En ocasiones resulta más conveniente utilizar β = v / c ( beta minúscula ) en lugar de v , de forma que se muestre mucho más claramente la simetría en la transformación. De los rangos permitidos de v y de la definición de β se deduce que −1 < β < 1. El uso de β y γ es estándar en toda la literatura. $${\displaystyle {\begin{aligned}ct'&=\gamma \left(ct-\beta x\right)\,,\\x'&=\gamma \left(x-\beta ct\right)\,,\\\end{aligned}}}$$

Cuando la velocidad de impulso está en una dirección vectorial arbitraria con el vector de impulso , entonces la transformación de un sistema de coordenadas de espacio-tiempo no primado a un sistema de coordenadas primado está dada por ^[14] ${\displaystyle {\boldsymbol {v}}}$ ${\displaystyle {\boldsymbol {\beta }}={\boldsymbol {v}}/c}$

$${\displaystyle {\begin{bmatrix}ct'{\vphantom {-\gamma \beta _{x}}}\\x'{\vphantom {1+{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}^{2}}}\\y'{\vphantom {{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}\beta _{y}}}\\z'{\vphantom {{\frac {\gamma ^{2}}{1+\gamma }}\beta _{y}\beta _{z}}}\end{bmatrix}}={\begin{bmatrix}\gamma &-\gamma \beta _{x}&-\gamma \beta _{y}&-\gamma \beta _{z}\\-\gamma \beta _{x}&1+{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}^{2}&{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}\beta _{y}&{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}\beta _{z}\\-\gamma \beta _{y}&{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}\beta _{y}&1+{\frac {\gamma ^{2}}{1+\gamma }}\beta _{y}^{2}&{\frac {\gamma ^{2}}{1+\gamma }}\beta _{y}\beta _{z}\\-\gamma \beta _{z}&{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}\beta _{z}&{\frac {\gamma ^{2}}{1+\gamma }}\beta _{y}\beta _{z}&1+{\frac {\gamma ^{2}}{1+\gamma }}\beta _{z}^{2}\\\end{bmatrix}}{\begin{bmatrix}ct{\vphantom {-\gamma \beta _{x}}}\\x{\vphantom {1+{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}^{2}}}\\y{\vphantom {{\frac {\gamma ^{2}}{1+\gamma }}\beta _{x}\beta _{y}}}\\z{\vphantom {{\frac {\gamma ^{2}}{1+\gamma }}\beta _{y}\beta _{z}}}\end{bmatrix}},}$$

donde el factor de Lorentz es . El determinante de la matriz de transformación es +1 y su traza es . La inversa de la transformación se obtiene invirtiendo el signo de . ${\displaystyle \gamma =1/{\sqrt {1-{\boldsymbol {\beta }}^{2}}}}$ ${\displaystyle 2(1+\gamma )}$ ${\displaystyle {\boldsymbol {\beta }}}$

Las transformaciones de Lorentz también se pueden derivar de una manera que se parezca a las rotaciones circulares en el espacio 3D utilizando las funciones hiperbólicas . Para el impulso en la dirección x , los resultados son

Impulso de Lorentz ( dirección x con rapidez ζ )

${\displaystyle {\begin{aligned}ct'&=ct\cosh \zeta -x\sinh \zeta \\x'&=x\cosh \zeta -ct\sinh \zeta \\y'&=y\\z'&=z\end{aligned}}}$

donde ζ ( zeta minúscula ) es un parámetro llamado rapidez (se utilizan muchos otros símbolos, incluidos θ, ϕ, φ, η, ψ, ξ ). Dada la gran semejanza con las rotaciones de coordenadas espaciales en el espacio 3d en los planos cartesianos xy, yz y zx, un impulso de Lorentz puede considerarse como una rotación hiperbólica de las coordenadas del espacio-tiempo en los planos cartesianos-temporales xt, yt y zt del espacio de Minkowski 4d . El parámetro ζ es el ángulo hiperbólico de rotación, análogo al ángulo ordinario para rotaciones circulares. Esta transformación puede ilustrarse con un diagrama de Minkowski .

Las funciones hiperbólicas surgen de la diferencia entre los cuadrados de las coordenadas temporales y espaciales en el intervalo espacio-temporal, en lugar de una suma. La significación geométrica de las funciones hiperbólicas se puede visualizar tomando x = 0 o ct = 0 en las transformaciones. Elevando al cuadrado y restando los resultados, se pueden derivar curvas hiperbólicas de valores de coordenadas constantes pero con ζ variable , lo que parametriza las curvas según la identidad $${\displaystyle \cosh ^{2}\zeta -\sinh ^{2}\zeta =1\,.}$$

Por el contrario, los ejes ct y x pueden construirse para coordenadas variables pero con ζ constante . La definición proporciona el vínculo entre un valor constante de rapidez y la pendiente del eje ct en el espacio-tiempo. Una consecuencia de estas dos fórmulas hiperbólicas es una identidad que coincide con el factor de Lorentz. $${\displaystyle \tanh \zeta ={\frac {\sinh \zeta }{\cosh \zeta }}\,,}$$ $${\displaystyle \cosh \zeta ={\frac {1}{\sqrt {1-\tanh ^{2}\zeta }}}\,.}$$

Comparando las transformaciones de Lorentz en términos de velocidad relativa y rapidez, o utilizando las fórmulas anteriores, las conexiones entre β , γ y ζ son $${\displaystyle {\begin{aligned}\beta &=\tanh \zeta \,,\\\gamma &=\cosh \zeta \,,\\\beta \gamma &=\sinh \zeta \,.\end{aligned}}}$$

Tomando la tangente hiperbólica inversa se obtiene la rapidez $${\displaystyle \zeta =\tanh ^{-1}\beta \,.}$$

Como −1 < β < 1 , se sigue −∞ < ζ < ∞ . De la relación entre ζ y β , la rapidez positiva ζ > 0 es movimiento a lo largo de las direcciones positivas de los ejes xx ′ , la rapidez cero ζ = 0 es ningún movimiento relativo, mientras que la rapidez negativa ζ < 0 es movimiento relativo a lo largo de las direcciones negativas de los ejes xx ′ .

Las transformaciones inversas se obtienen intercambiando cantidades cebadas y no cebadas para cambiar los marcos de coordenadas y negando la rapidez ζ → − ζ ya que esto es equivalente a negar la velocidad relativa. Por lo tanto,

Impulso de Lorentz inverso ( dirección x con rapidez ζ )

${\displaystyle {\begin{aligned}ct&=ct'\cosh \zeta +x'\sinh \zeta \\x&=x'\cosh \zeta +ct'\sinh \zeta \\y&=y'\\z&=z'\end{aligned}}}$

Las transformaciones inversas se pueden visualizar de manera similar considerando los casos en que x ′ = 0 y ct ′ = 0 .

Hasta ahora, las transformaciones de Lorentz se han aplicado a un evento . Si hay dos eventos, existe una separación espacial y un intervalo de tiempo entre ellos. De la linealidad de las transformaciones de Lorentz se deduce que se pueden elegir dos valores de coordenadas espaciales y temporales, se pueden aplicar las transformaciones de Lorentz a cada uno y luego restarlas para obtener las transformaciones de Lorentz de las diferencias;

$${\displaystyle {\begin{aligned}\Delta t'&=\gamma \left(\Delta t-{\frac {v\,\Delta x}{c^{2}}}\right)\,,\\\Delta x'&=\gamma \left(\Delta x-v\,\Delta t\right)\,,\end{aligned}}}$$con relaciones inversas $${\displaystyle {\begin{aligned}\Delta t&=\gamma \left(\Delta t'+{\frac {v\,\Delta x'}{c^{2}}}\right)\,,\\\Delta x&=\gamma \left(\Delta x'+v\,\Delta t'\right)\,.\end{aligned}}}$$

donde Δ ( delta mayúscula ) indica una diferencia de cantidades; por ejemplo, Δ x = x ₂ − x ₁ para dos valores de coordenadas x , y así sucesivamente.

Estas transformaciones en diferencias en lugar de puntos espaciales o instantes de tiempo son útiles por varias razones:

• En cálculos y experimentos, son las longitudes entre dos puntos o intervalos de tiempo los que se miden o son de interés (por ejemplo, la longitud de un vehículo en movimiento o el tiempo que lleva viajar de un lugar a otro).
• Las transformaciones de velocidad se pueden derivar fácilmente haciendo la diferencia infinitesimalmente pequeña y dividiendo las ecuaciones, y repitiendo el proceso para la transformación de la aceleración.
• Si los sistemas de coordenadas nunca coinciden (es decir, no están en la configuración estándar), y si ambos observadores pueden estar de acuerdo en un evento t ₀ , x ₀ , y ₀ , z ₀ en F y t ₀ ′, x ₀ ′, y ₀ ′, z ₀ ′ en F ′ , entonces pueden usar ese evento como origen, y las diferencias de coordenadas del espacio-tiempo son las diferencias entre sus coordenadas y este origen, por ejemplo, Δ x = x − x ₀ , Δ x ′ = x ′ − x ₀ ′ , etc.

Implicaciones físicas

Un requisito crítico de las transformaciones de Lorentz es la invariancia de la velocidad de la luz, un hecho utilizado en su derivación y contenido en las propias transformaciones. Si en F la ecuación para un pulso de luz a lo largo de la dirección x es x = ct , entonces en F ′ las transformaciones de Lorentz dan x ′ = ct ′ , y viceversa, para cualquier − c < v < c .

Para velocidades relativas mucho menores que la velocidad de la luz, las transformaciones de Lorentz se reducen a la transformación de Galileo de acuerdo con el principio de correspondencia . A veces se dice que la física no relativista es una física de "acción instantánea a distancia". ^[15] $${\displaystyle {\begin{aligned}t'&\approx t\\x'&\approx x-vt\end{aligned}}}$$

Tres predicciones contraintuitivas, pero correctas, de las transformaciones son:

Relatividad de la simultaneidad

Supongamos que dos eventos ocurren a lo largo del eje x simultáneamente ( Δ t = 0 ) en F , pero separados por un desplazamiento distinto de cero Δ x . Entonces en F ′ , encontramos que , por lo que los eventos ya no son simultáneos según un observador en movimiento. ${\displaystyle \Delta t'=\gamma {\frac {-v\,\Delta x}{c^{2}}}}$

Dilatación del tiempo

Supóngase que hay un reloj en reposo en F . Si se mide un intervalo de tiempo en el mismo punto de ese marco, de modo que Δ x = 0 , entonces las transformaciones dan este intervalo en F ′ por Δ t ′ = γ Δ t . A la inversa, supóngase que hay un reloj en reposo en F ′ . Si se mide un intervalo en el mismo punto de ese marco, de modo que Δ x ′ = 0 , entonces las transformaciones dan este intervalo en F por Δ t = γ Δ t ′ . De cualquier manera, cada observador mide el intervalo de tiempo entre los tictacs de un reloj en movimiento como más largo por un factor γ que el intervalo de tiempo entre los tictacs de su propio reloj.

Contracción de longitud

Supongamos que hay una varilla en reposo en F alineada a lo largo del eje x, con longitud Δ x . En F ′ , la varilla se mueve con velocidad - v , por lo que su longitud debe medirse tomando dos mediciones simultáneas ( Δ t ′ = 0 ) en extremos opuestos. Bajo estas condiciones, la transformada inversa de Lorentz muestra que Δ x = γ Δ x ′ . En F las dos mediciones ya no son simultáneas, pero esto no importa porque la varilla está en reposo en F . Entonces, cada observador mide la distancia entre los puntos finales de una varilla en movimiento y resulta ser más corta por un factor 1/ γ que los puntos finales de una varilla idéntica en reposo en su propio marco. La contracción de la longitud afecta a cualquier cantidad geométrica relacionada con las longitudes, por lo que desde la perspectiva de un observador en movimiento, las áreas y los volúmenes también parecerán encogerse a lo largo de la dirección del movimiento.

Transformaciones vectoriales

Un observador en el marco F observa que F ′ se mueve con velocidad v , mientras que F ′ observa que F se mueve con velocidad − v . Los ejes de coordenadas de cada marco siguen siendo paralelos ^{[ ¿según quién? ]} y ortogonales. El vector de posición medido en cada marco se divide en componentes paralelos y perpendiculares al vector de velocidad relativa v .
Izquierda: Configuración estándar. Derecha: Configuración inversa.

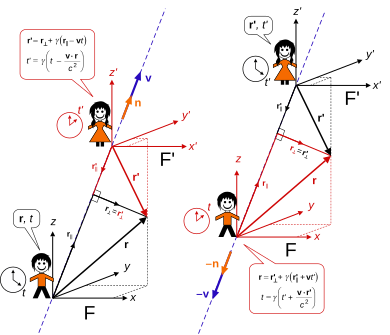
El uso de vectores permite expresar posiciones y velocidades en direcciones arbitrarias de forma compacta. Un impulso único en cualquier dirección depende del vector de velocidad relativa completo v con una magnitud | v | = v que no puede ser igual o mayor que c , de modo que 0 ≤ v < c .

Solo cambian el tiempo y las coordenadas paralelas a la dirección del movimiento relativo, mientras que las coordenadas perpendiculares no. Con esto en mente, divida el vector de posición espacial r medido en F y r ′ medido en F′ , cada uno en componentes perpendiculares (⊥) y paralelas (‖) a v , entonces las transformaciones son donde · es el producto escalar . El factor de Lorentz γ conserva su definición para un impulso en cualquier dirección, ya que depende solo de la magnitud de la velocidad relativa. La definición β = v / c con magnitud 0 ≤ β < 1 también es utilizada por algunos autores. $${\displaystyle \mathbf {r} =\mathbf {r} _{\perp }+\mathbf {r} _{\|}\,,\quad \mathbf {r} '=\mathbf {r} _{\perp }'+\mathbf {r} _{\|}'\,,}$$ $${\displaystyle {\begin{aligned}t'&=\gamma \left(t-{\frac {\mathbf {r} _{\parallel }\cdot \mathbf {v} }{c^{2}}}\right)\\\mathbf {r} _{\|}'&=\gamma (\mathbf {r} _{\|}-\mathbf {v} t)\\\mathbf {r} _{\perp }'&=\mathbf {r} _{\perp }\end{aligned}}}$$

Introduciendo un vector unitario n = v / v = β / β en la dirección del movimiento relativo, la velocidad relativa es v = v n con magnitud v y dirección n , y la proyección y el rechazo del vector dan respectivamente $${\displaystyle \mathbf {r} _{\parallel }=(\mathbf {r} \cdot \mathbf {n} )\mathbf {n} \,,\quad \mathbf {r} _{\perp }=\mathbf {r} -(\mathbf {r} \cdot \mathbf {n} )\mathbf {n} }$$

La acumulación de resultados da las transformaciones completas,

Impulso de Lorentz ( en dirección n con magnitud v )

${\displaystyle {\begin{aligned}t'&=\gamma \left(t-{\frac {v\mathbf {n} \cdot \mathbf {r} }{c^{2}}}\right)\,,\\\mathbf {r} '&=\mathbf {r} +(\gamma -1)(\mathbf {r} \cdot \mathbf {n} )\mathbf {n} -\gamma tv\mathbf {n} \,.\end{aligned}}}$

La proyección y el rechazo también se aplican a r ′ . Para las transformaciones inversas, intercambie r y r ′ para cambiar las coordenadas observadas y niegue la velocidad relativa v → − v (o simplemente el vector unitario n → − n ya que la magnitud v siempre es positiva) para obtener

Impulso de Lorentz inverso ( en dirección n con magnitud v )

${\displaystyle {\begin{aligned}t&=\gamma \left(t'+{\frac {\mathbf {r} '\cdot v\mathbf {n} }{c^{2}}}\right)\,,\\\mathbf {r} &=\mathbf {r} '+(\gamma -1)(\mathbf {r} '\cdot \mathbf {n} )\mathbf {n} +\gamma t'v\mathbf {n} \,,\end{aligned}}}$

El vector unitario tiene la ventaja de simplificar las ecuaciones para un único impulso, permite restablecer v o β cuando sea conveniente y la parametrización de rapidez se obtiene inmediatamente reemplazando β y βγ . No es conveniente para múltiples impulsos.

La relación vectorial entre la velocidad relativa y la rapidez es ^[16] y el "vector de rapidez" se puede definir como cada uno de los cuales sirve como una abreviatura útil en algunos contextos. La magnitud de ζ es el valor absoluto del escalar de rapidez confinado a 0 ≤ ζ < ∞ , lo que coincide con el rango 0 ≤ β < 1 . $${\displaystyle {\boldsymbol {\beta }}=\beta \mathbf {n} =\mathbf {n} \tanh \zeta \,,}$$ $${\displaystyle {\boldsymbol {\zeta }}=\zeta \mathbf {n} =\mathbf {n} \tanh ^{-1}\beta \,,}$$

Transformación de velocidades

La transformación de velocidades proporciona la definición de suma de velocidades relativista ⊕ , el orden de los vectores se elige para reflejar el orden de la suma de velocidades; primero v (la velocidad de F′ relativa a F) luego u ′ (la velocidad de X relativa a F′) para obtener u = v ⊕ u ′ (la velocidad de X relativa a F).

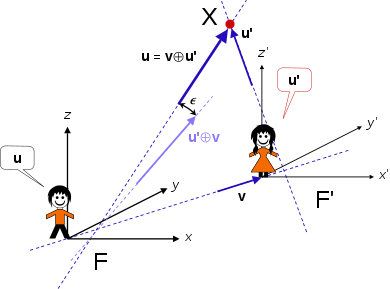
Definición de las velocidades de coordenadas y el factor de Lorentz mediante

${\displaystyle \mathbf {u} ={\frac {d\mathbf {r} }{dt}}\,,\quad \mathbf {u} '={\frac {d\mathbf {r} '}{dt'}}\,,\quad \gamma _{\mathbf {v} }={\frac {1}{\sqrt {1-{\dfrac {\mathbf {v} \cdot \mathbf {v} }{c^{2}}}}}}}$

Tomando las diferenciales en las coordenadas y el tiempo de las transformaciones vectoriales, luego dividiendo las ecuaciones, se llega a

${\displaystyle \mathbf {u} '={\frac {1}{1-{\frac {\mathbf {v} \cdot \mathbf {u} }{c^{2}}}}}\left[{\frac {\mathbf {u} }{\gamma _{\mathbf {v} }}}-\mathbf {v} +{\frac {1}{c^{2}}}{\frac {\gamma _{\mathbf {v} }}{\gamma _{\mathbf {v} }+1}}\left(\mathbf {u} \cdot \mathbf {v} \right)\mathbf {v} \right]}$

Las velocidades u y u ′ son la velocidad de algún objeto masivo. También pueden ser para un tercer sistema inercial (digamos F ′′), en cuyo caso deben ser constantes . Denotemos cada entidad por X. Entonces X se mueve con velocidad u relativa a F, o equivalentemente con velocidad u ′ relativa a F′, a su vez F′ se mueve con velocidad v relativa a F. Las transformaciones inversas se pueden obtener de manera similar, o como con las coordenadas de posición intercambiar u y u ′ , y cambiar v a − v .

La transformación de la velocidad es útil en la aberración estelar , el experimento de Fizeau y el efecto Doppler relativista .

Las transformaciones de Lorentz de la aceleración se pueden obtener de manera similar tomando diferenciales en los vectores de velocidad y dividiéndolos por el diferencial de tiempo.

Transformación de otras magnitudes

En general, dadas cuatro cantidades A y Z = ( Z _x , Z _y , Z _z ) y sus contrapartes potenciadas por Lorentz A ′ y Z ′ = ( Z ′ _x , Z ′ _y , Z ′ _z ) , una relación de la forma implica que las cantidades se transforman bajo transformaciones de Lorentz similares a la transformación de las coordenadas del espacio-tiempo; $${\displaystyle A^{2}-\mathbf {Z} \cdot \mathbf {Z} ={A'}^{2}-\mathbf {Z} '\cdot \mathbf {Z} '}$$ $${\displaystyle {\begin{aligned}A'&=\gamma \left(A-{\frac {v\mathbf {n} \cdot \mathbf {Z} }{c}}\right)\,,\\\mathbf {Z} '&=\mathbf {Z} +(\gamma -1)(\mathbf {Z} \cdot \mathbf {n} )\mathbf {n} -{\frac {\gamma Av\mathbf {n} }{c}}\,.\end{aligned}}}$$

La descomposición de Z (y Z ′ ) en componentes perpendiculares y paralelas a v es exactamente la misma que para el vector de posición, como lo es el proceso de obtener las transformaciones inversas (intercambiar ( A , Z ) y ( A ′, Z ′) para intercambiar las cantidades observadas e invertir la dirección del movimiento relativo mediante la sustitución n ↦ − n ).

Las cantidades ( A , Z ) forman colectivamente un cuatrivector , donde A es el "componente temporal" y Z el "componente espacial". Los ejemplos de A y Z son los siguientes:

Para un objeto dado (por ejemplo, partícula, fluido, campo, material), si A o Z corresponden a propiedades específicas del objeto como su densidad de carga , densidad de masa , espín , etc., sus propiedades pueden fijarse en el marco de referencia en reposo de ese objeto. Entonces las transformaciones de Lorentz dan las propiedades correspondientes en un marco de referencia que se mueve en relación con el objeto con velocidad constante. Esto rompe algunas nociones que se dan por sentadas en la física no relativista. Por ejemplo, la energía E de un objeto es un escalar en la mecánica no relativista, pero no en la mecánica relativista porque la energía cambia bajo las transformaciones de Lorentz; su valor es diferente para varios marcos inerciales. En el marco de referencia en reposo de un objeto, tiene una energía en reposo y un momento cero. En un marco potenciado su energía es diferente y parece tener un momento. De manera similar, en la mecánica cuántica no relativista el espín de una partícula es un vector constante, pero en la mecánica cuántica relativista el espín s depende del movimiento relativo. En el marco de reposo de la partícula, el pseudovector de espín se puede fijar para que sea su espín no relativista ordinario con una cantidad temporal cero s _t , sin embargo, un observador mejorado percibirá un componente temporal distinto de cero y un espín alterado. ^[17]

No todas las cantidades son invariantes en la forma que se muestra arriba, por ejemplo el momento angular orbital L no tiene una cantidad temporal, y tampoco la tienen el campo eléctrico E ni el campo magnético B. La definición de momento angular es L = r × p , y en un marco potenciado el momento angular alterado es L ′ = r ′ × p ′ . La aplicación de esta definición usando las transformaciones de coordenadas y momento conduce a la transformación del momento angular. Resulta que L se transforma con otra cantidad vectorial N = ( E / c ² ) r − t p relacionada con los refuerzos, vea el momento angular relativista para más detalles. Para el caso de los campos E y B , las transformaciones no se pueden obtener directamente usando álgebra vectorial. La fuerza de Lorentz es la definición de estos campos, y en F es F = q ( E + v × B ) mientras que en F ′ es F ′ = q ( E ′ + v ′ × B ′) . Un método para derivar las transformaciones del campo EM de una manera eficiente que también ilustra la unidad del campo electromagnético utiliza el álgebra tensorial, que se muestra a continuación.

Formulación matemática

En todo el texto, las letras mayúsculas en cursiva (no negrita) son matrices de 4×4, mientras que las letras en negrita (no cursiva) son matrices de 3×3.

Grupo de Lorentz homogéneo

Escribiendo las coordenadas en vectores de columna y la métrica de Minkowski η como una matriz cuadrada, el intervalo espacio-temporal toma la forma (el superíndice T denota transposición ) y es invariante bajo una transformación de Lorentz donde Λ es una matriz cuadrada que puede depender de parámetros. $${\displaystyle X'={\begin{bmatrix}c\,t'\\x'\\y'\\z'\end{bmatrix}}\,,\quad \eta ={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}\,,\quad X={\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}}}$$ $${\displaystyle X\cdot X=X^{\mathrm {T} }\eta X={X'}^{\mathrm {T} }\eta {X'}}$$ $${\displaystyle X'=\Lambda X}$$

El conjunto de todas las transformaciones de Lorentz en este artículo se denota como . Este conjunto junto con la multiplicación de matrices forma un grupo , en este contexto conocido como el grupo de Lorentz . Además, la expresión anterior X · X es una forma cuadrática de la signatura (3,1) en el espacio-tiempo, y el grupo de transformaciones que deja esta forma cuadrática invariante es el grupo ortogonal indefinido O(3,1), un grupo de Lie . En otras palabras, el grupo de Lorentz es O(3,1). Como se presenta en este artículo, todos los grupos de Lie mencionados son grupos de Lie de matrices . En este contexto, la operación de composición equivale a la multiplicación de matrices . ${\displaystyle \Lambda }$ ${\displaystyle {\mathcal {L}}}$

De la invariancia del intervalo espacio-temporal se sigue que esta ecuación matricial contiene las condiciones generales de la transformación de Lorentz para asegurar la invariancia del intervalo espacio-temporal. Tomando el determinante de la ecuación utilizando la regla del producto ^{[nb 4]} se obtiene inmediatamente $${\displaystyle \eta =\Lambda ^{\mathrm {T} }\eta \Lambda }$$ $${\displaystyle \left[\det(\Lambda )\right]^{2}=1\quad \Rightarrow \quad \det(\Lambda )=\pm 1}$$

Al escribir la métrica de Minkowski como una matriz de bloques y la transformación de Lorentz en la forma más general, al realizar las multiplicaciones de matrices de bloques se obtienen condiciones generales sobre Γ, a , b , M para asegurar la invariancia relativista. No se puede extraer mucha información directamente de todas las condiciones, sin embargo, uno de los resultados es útil; b ^T b ≥ 0 siempre, por lo que se deduce que $${\displaystyle \eta ={\begin{bmatrix}-1&0\\0&\mathbf {I} \end{bmatrix}}\,,\quad \Lambda ={\begin{bmatrix}\Gamma &-\mathbf {a} ^{\mathrm {T} }\\-\mathbf {b} &\mathbf {M} \end{bmatrix}}\,,}$$ $${\displaystyle \Gamma ^{2}=1+\mathbf {b} ^{\mathrm {T} }\mathbf {b} }$$ $${\displaystyle \Gamma ^{2}\geq 1\quad \Rightarrow \quad \Gamma \leq -1\,,\quad \Gamma \geq 1}$$

La desigualdad negativa puede ser inesperada, porque Γ multiplica la coordenada temporal y esto tiene un efecto sobre la simetría temporal . Si se cumple la igualdad positiva, entonces Γ es el factor de Lorentz.

El determinante y la desigualdad proporcionan cuatro formas de clasificar las transformaciones de Loentz ( en adelante, LT , por brevedad ). Cualquier LT particular tiene solo un signo determinante y solo una desigualdad. Hay cuatro conjuntos que incluyen cada par posible dado por las intersecciones (símbolo en forma de "n" que significa "y") de estos conjuntos de clasificación.

donde "+" y "−" indican el signo determinante, mientras que "↑" para ≥ y "↓" para ≤ denotan las desigualdades.

El grupo de Lorentz completo se divide en la unión (símbolo en forma de "u" que significa "o") de cuatro conjuntos disjuntos $${\displaystyle {\mathcal {L}}={\mathcal {L}}_{+}^{\uparrow }\cup {\mathcal {L}}_{-}^{\uparrow }\cup {\mathcal {L}}_{+}^{\downarrow }\cup {\mathcal {L}}_{-}^{\downarrow }}$$

Un subgrupo de un grupo debe estar cerrado bajo la misma operación del grupo (aquí, multiplicación de matrices). En otras palabras, para dos transformaciones de Lorentz Λ y L de un subgrupo particular, las transformaciones de Lorentz compuestas Λ L y L Λ deben estar en el mismo subgrupo que Λ y L . Este no siempre es el caso: la composición de dos transformaciones de Lorentz antícronas es ortócrona, y la composición de dos transformaciones de Lorentz impropias es propia. En otras palabras, mientras que los conjuntos , , , y todos forman subgrupos, los conjuntos que contienen transformaciones impropias y/o antícronas sin suficientes transformaciones ortócronas propias (por ejemplo , , , ) no forman subgrupos. ${\displaystyle {\mathcal {L}}_{+}^{\uparrow }}$ ${\displaystyle {\mathcal {L}}_{+}}$ ${\displaystyle {\mathcal {L}}^{\uparrow }}$ ${\displaystyle {\mathcal {L}}_{0}={\mathcal {L}}_{+}^{\uparrow }\cup {\mathcal {L}}_{-}^{\downarrow }}$ ${\displaystyle {\mathcal {L}}_{+}^{\downarrow }}$ ${\displaystyle {\mathcal {L}}_{-}^{\downarrow }}$ ${\displaystyle {\mathcal {L}}_{-}^{\uparrow }}$

Transformaciones adecuadas

Si se mide un 4-vector covariante de Lorentz en un marco inercial con resultado , y la misma medición realizada en otro marco inercial (con la misma orientación y origen) da como resultado , los dos resultados estarán relacionados por donde la matriz de impulso representa la transformación de Lorentz sin rotación entre los marcos no primados y primados y es la velocidad del marco primado vista desde el marco no primado. La matriz está dada por ^[18] ${\displaystyle X}$ ${\displaystyle X'}$ $${\displaystyle X'=B(\mathbf {v} )X}$$ ${\displaystyle B(\mathbf {v} )}$ ${\displaystyle \mathbf {v} }$ $${\displaystyle B(\mathbf {v} )={\begin{bmatrix}\gamma &-\gamma v_{x}/c&-\gamma v_{y}/c&-\gamma v_{z}/c\\-\gamma v_{x}/c&1+(\gamma -1){\dfrac {v_{x}^{2}}{v^{2}}}&(\gamma -1){\dfrac {v_{x}v_{y}}{v^{2}}}&(\gamma -1){\dfrac {v_{x}v_{z}}{v^{2}}}\\-\gamma v_{y}/c&(\gamma -1){\dfrac {v_{y}v_{x}}{v^{2}}}&1+(\gamma -1){\dfrac {v_{y}^{2}}{v^{2}}}&(\gamma -1){\dfrac {v_{y}v_{z}}{v^{2}}}\\-\gamma v_{z}/c&(\gamma -1){\dfrac {v_{z}v_{x}}{v^{2}}}&(\gamma -1){\dfrac {v_{z}v_{y}}{v^{2}}}&1+(\gamma -1){\dfrac {v_{z}^{2}}{v^{2}}}\end{bmatrix}}={\begin{bmatrix}\gamma &-\gamma {\vec {\beta }}^{T}\\-\gamma {\vec {\beta }}&I+(\gamma -1){\dfrac {{\vec {\beta }}{\vec {\beta }}^{T}}{\beta ^{2}}}\end{bmatrix}},}$$

donde es la magnitud de la velocidad y es el factor de Lorentz. Esta fórmula representa una transformación pasiva, ya que describe cómo cambian las coordenadas de la cantidad medida del marco sin primar al marco con primar. La transformación activa está dada por . ${\textstyle v={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}}$ ${\textstyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$ ${\displaystyle B(-\mathbf {v} )}$

Si un marco F ′ es impulsado con velocidad u relativa al marco F , y otro marco F ′′ es impulsado con velocidad v relativa a F ′ , los impulsos separados son y la composición de los dos impulsos conecta las coordenadas en F ′′ y F , Las transformaciones sucesivas actúan sobre la izquierda. Si u y v son colineales (paralelas o antiparalelas a lo largo de la misma línea de movimiento relativo), las matrices de impulso conmutan : B ( v ) B ( u ) = B ( u ) B ( v ) . Esta transformación compuesta resulta ser otro impulso, B ( w ) , donde w es colineal con u y v . $${\displaystyle X''=B(\mathbf {v} )X'\,,\quad X'=B(\mathbf {u} )X}$$ $${\displaystyle X''=B(\mathbf {v} )B(\mathbf {u} )X\,.}$$

Si u y v no son colineales sino que están en direcciones diferentes, la situación es considerablemente más complicada. Los boosts de Lorentz a lo largo de direcciones diferentes no conmutan: B ( v ) B ( u ) y B ( u ) B ( v ) no son iguales. Aunque cada una de estas composiciones no es un boost único, cada composición sigue siendo una transformación de Lorentz ya que preserva el intervalo de espacio-tiempo. Resulta que la composición de dos boosts de Lorentz cualesquiera es equivalente a un boost seguido o precedido por una rotación en las coordenadas espaciales, en la forma de R ( ρ ) B ( w ) o B ( w ) R ( ρ ) . Los w y w son velocidades compuestas , mientras que ρ y ρ son parámetros de rotación (por ejemplo, variables de eje-ángulo , ángulos de Euler , etc.). La rotación en forma de matriz de bloques es simplemente donde R ( ρ ) es una matriz de rotación 3d , que rota cualquier vector 3d en un sentido (transformación activa), o equivalentemente el marco de coordenadas en el sentido opuesto (transformación pasiva). No es simple conectar w y ρ (o w y ρ ) a los parámetros de impulso originales u y v . En una composición de impulsos, la matriz R se denomina rotación de Wigner y da lugar a la precesión de Thomas . Estos artículos dan las fórmulas explícitas para las matrices de transformación compuestas, incluidas expresiones para w , ρ , w , ρ . $${\displaystyle \quad R({\boldsymbol {\rho }})={\begin{bmatrix}1&0\\0&\mathbf {R} ({\boldsymbol {\rho }})\end{bmatrix}}\,,}$$

En este artículo se utiliza la representación eje-ángulo para ρ . La rotación se realiza alrededor de un eje en la dirección de un vector unitario e , a través del ángulo θ (positivo en sentido antihorario, negativo en sentido horario, según la regla de la mano derecha ). El "vector eje-ángulo" servirá como una abreviatura útil. $${\displaystyle {\boldsymbol {\theta }}=\theta \mathbf {e} }$$

Las rotaciones espaciales por sí solas también son transformaciones de Lorentz, ya que dejan invariable el intervalo espacio-temporal. Al igual que los impulsos, las rotaciones sucesivas sobre ejes diferentes no se conmutan. A diferencia de los impulsos, la composición de dos rotaciones cualesquiera es equivalente a una sola rotación. Algunas otras similitudes y diferencias entre las matrices de impulso y rotación incluyen:

• inversas : B ( v ) ⁻¹ = B (− v ) (movimiento relativo en dirección opuesta), y R ( θ ) ⁻¹ = R (− θ ) (rotación en sentido opuesto sobre el mismo eje)
• Transformación de identidad para ausencia de movimiento relativo/rotación: B ( 0 ) = R ( 0 ) = I
• determinante unitario : det( B ) = det( R ) = +1 . Esta propiedad las convierte en transformaciones propias.
• simetría matricial : B es simétrica (igual ^a transpuesta ), mientras que R no es simétrica pero ortogonal (transpuesta igual a inversa , RT = R ⁻¹ ).

La transformación de Lorentz propia más general Λ( v , θ ) incluye un impulso y una rotación juntos, y es una matriz no simétrica. Como casos especiales, Λ( 0 , θ ) = R ( θ ) y Λ( v , 0 ) = B ( v ) . Una forma explícita de la transformación de Lorentz general es complicada de escribir y no se dará aquí. Sin embargo, se darán a continuación expresiones de forma cerrada para las matrices de transformación utilizando argumentos teóricos de grupo. Será más fácil utilizar la parametrización de rapidez para impulsos, en cuyo caso se escribe Λ( ζ , θ ) y B ( ζ ) .

El grupo Lie SO⁺(3,1)

El conjunto de transformaciones con multiplicación de matrices como operación de composición forma un grupo, llamado "grupo restringido de Lorentz", y es el grupo ortogonal indefinido especial SO ⁺ (3,1). (El signo más indica que conserva la orientación de la dimensión temporal). $${\displaystyle \{B({\boldsymbol {\zeta }}),R({\boldsymbol {\theta }}),\Lambda ({\boldsymbol {\zeta }},{\boldsymbol {\theta }})\}}$$

Para simplificar, observe el impulso infinitesimal de Lorentz en la dirección x (examinar un impulso en cualquier otra dirección, o una rotación sobre cualquier eje, sigue un procedimiento idéntico). El impulso infinitesimal es un pequeño impulso que se aleja de la identidad, obtenido por la expansión de Taylor de la matriz de impulso hasta el primer orden alrededor de ζ = 0 , donde los términos de orden superior que no se muestran son despreciables porque ζ es pequeño y B _x es simplemente la matriz de impulso en la dirección x . La derivada de la matriz es la matriz de derivadas (de las entradas, con respecto a la misma variable), y se entiende que las derivadas se encuentran primero y luego se evalúan en ζ = 0 . $${\displaystyle B_{x}=I+\zeta \left.{\frac {\partial B_{x}}{\partial \zeta }}\right|_{\zeta =0}+\cdots }$$ $${\displaystyle \left.{\frac {\partial B_{x}}{\partial \zeta }}\right|_{\zeta =0}=-K_{x}\,.}$$

Por ahora, K _x se define por este resultado (su significado se explicará en breve). En el límite de un número infinito de pasos infinitamente pequeños, se obtiene la transformación finita de boost en forma de exponencial matricial donde se ha utilizado la definición límite de la exponencial (ver también caracterizaciones de la función exponencial ). De manera más general ^{[nb 5]} $${\displaystyle B_{x}=\lim _{N\to \infty }\left(I-{\frac {\zeta }{N}}K_{x}\right)^{N}=e^{-\zeta K_{x}}}$$

$${\displaystyle B({\boldsymbol {\zeta }})=e^{-{\boldsymbol {\zeta }}\cdot \mathbf {K} }\,,\quad R({\boldsymbol {\theta }})=e^{{\boldsymbol {\theta }}\cdot \mathbf {J} }\,.}$$

El vector eje-ángulo θ y el vector de rapidez ζ son en total seis variables continuas que forman los parámetros del grupo (en esta representación particular), y los generadores del grupo son K = ( K _x , K _y , K _z ) y J = ( J _x , J _y , J _z ) , cada uno vectores de matrices con las formas explícitas ^{[nb 6]}

$${\displaystyle {\begin{alignedat}{3}K_{x}&={\begin{bmatrix}0&1&0&0\\1&0&0&0\\0&0&0&0\\0&0&0&0\\\end{bmatrix}}\,,\quad &K_{y}&={\begin{bmatrix}0&0&1&0\\0&0&0&0\\1&0&0&0\\0&0&0&0\end{bmatrix}}\,,\quad &K_{z}&={\begin{bmatrix}0&0&0&1\\0&0&0&0\\0&0&0&0\\1&0&0&0\end{bmatrix}}\\[10mu]J_{x}&={\begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&0&-1\\0&0&1&0\\\end{bmatrix}}\,,\quad &J_{y}&={\begin{bmatrix}0&0&0&0\\0&0&0&1\\0&0&0&0\\0&-1&0&0\end{bmatrix}}\,,\quad &J_{z}&={\begin{bmatrix}0&0&0&0\\0&0&-1&0\\0&1&0&0\\0&0&0&0\end{bmatrix}}\end{alignedat}}}$$

Todos ellos se definen de forma análoga a K _x anterior, aunque los signos menos en los generadores de impulso son convencionales. Físicamente, los generadores del grupo de Lorentz corresponden a simetrías importantes en el espacio-tiempo: J son los generadores de rotación que corresponden al momento angular , y K son los generadores de impulso que corresponden al movimiento del sistema en el espacio-tiempo. La derivada de cualquier curva suave C ( t ) con C (0) = I en el grupo que depende de algún parámetro de grupo t con respecto a ese parámetro de grupo, evaluado en t = 0 , sirve como definición de un generador de grupo correspondiente G , y esto refleja una transformación infinitesimal que se aleja de la identidad. La curva suave siempre se puede tomar como exponencial, ya que la exponencial siempre mapeará G suavemente de nuevo en el grupo a través de t → exp( tG ) para todo t ; esta curva producirá G nuevamente cuando se diferencie en t = 0 .

Al expandir las exponenciales en sus series de Taylor se obtiene que reproduce de manera compacta las matrices de impulso y rotación dadas en la sección anterior. $${\displaystyle B({\boldsymbol {\zeta }})=I-\sinh \zeta (\mathbf {n} \cdot \mathbf {K} )+(\cosh \zeta -1)(\mathbf {n} \cdot \mathbf {K} )^{2}}$$ $${\displaystyle R({\boldsymbol {\theta }})=I+\sin \theta (\mathbf {e} \cdot \mathbf {J} )+(1-\cos \theta )(\mathbf {e} \cdot \mathbf {J} )^{2}\,.}$$

Se ha afirmado que la transformación general propia de Lorentz es un producto de un impulso y una rotación. En el nivel infinitesimal, el producto es conmutativo porque solo se requieren términos lineales (productos como ( θ · J )( ζ · K ) y ( ζ · K )( θ · J ) cuentan como términos de orden superior y son despreciables). Tomando el límite como antes, se llega a la transformación finita en forma de exponencial. $${\displaystyle {\begin{aligned}\Lambda &=(I-{\boldsymbol {\zeta }}\cdot \mathbf {K} +\cdots )(I+{\boldsymbol {\theta }}\cdot \mathbf {J} +\cdots )\\&=(I+{\boldsymbol {\theta }}\cdot \mathbf {J} +\cdots )(I-{\boldsymbol {\zeta }}\cdot \mathbf {K} +\cdots )\\&=I-{\boldsymbol {\zeta }}\cdot \mathbf {K} +{\boldsymbol {\theta }}\cdot \mathbf {J} +\cdots \end{aligned}}}$$ $${\displaystyle \Lambda ({\boldsymbol {\zeta }},{\boldsymbol {\theta }})=e^{-{\boldsymbol {\zeta }}\cdot \mathbf {K} +{\boldsymbol {\theta }}\cdot \mathbf {J} }.}$$

El caso inverso también es cierto, pero la descomposición de una transformación general finita de Lorentz en dichos factores no es trivial. En particular, porque los generadores no conmutan. Para una descripción de cómo encontrar los factores de una transformación general de Lorentz en términos de un impulso y una rotación en principio (esto generalmente no produce una expresión inteligible en términos de generadores J y K ), consulte la rotación de Wigner . Si, por otro lado, la descomposición se da en términos de los generadores, y uno quiere encontrar el producto en términos de los generadores, entonces se aplica la fórmula de Baker–Campbell–Hausdorff . $${\displaystyle e^{-{\boldsymbol {\zeta }}\cdot \mathbf {K} +{\boldsymbol {\theta }}\cdot \mathbf {J} }\neq e^{-{\boldsymbol {\zeta }}\cdot \mathbf {K} }e^{{\boldsymbol {\theta }}\cdot \mathbf {J} },}$$

El álgebra de Lie so(3,1)

Los generadores de Lorentz se pueden sumar o multiplicar por números reales para obtener más generadores de Lorentz. En otras palabras, el conjunto de todos los generadores de Lorentz junto con las operaciones de suma de matrices ordinarias y multiplicación de una matriz por un número , forma un espacio vectorial sobre los números reales. ^{[nb 7]} Los generadores J _x , J _y , J _z , K _x , K _y , K _z forman un conjunto base de V , y los componentes de los vectores de eje-ángulo y rapidez, θ _x , θ _y , θ _z , ζ _x , ζ _y , ζ _z , son las coordenadas de un generador de Lorentz con respecto a esta base. ^{[nb 8]} $${\displaystyle V=\{{\boldsymbol {\zeta }}\cdot \mathbf {K} +{\boldsymbol {\theta }}\cdot \mathbf {J} \}}$$

Tres de las relaciones de conmutación de los generadores de Lorentz son donde el corchete [ A , B ] = AB − BA se conoce como el conmutador , y las otras relaciones se pueden encontrar tomando permutaciones cíclicas de los componentes x, y, z (es decir, cambiar x a y, y a z, y z a x, repetir). $${\displaystyle [J_{x},J_{y}]=J_{z}\,,\quad [K_{x},K_{y}]=-J_{z}\,,\quad [J_{x},K_{y}]=K_{z}\,,}$$

Estas relaciones de conmutación, y el espacio vectorial de generadores, cumplen la definición del álgebra de Lie . En resumen, un álgebra de Lie se define como un espacio vectorial V sobre un cuerpo de números, y con una operación binaria [ , ] (llamada corchete de Lie en este contexto) sobre los elementos del espacio vectorial, que satisface los axiomas de bilinealidad , alternatización y la identidad de Jacobi . Aquí la operación [ , ] es el conmutador que satisface todos estos axiomas, el espacio vectorial es el conjunto de generadores de Lorentz V como se dio anteriormente, y el cuerpo es el conjunto de números reales. ${\displaystyle {\mathfrak {so}}(3,1)}$

Terminología de enlace utilizada en matemáticas y física: un generador de grupo es cualquier elemento del álgebra de Lie. Un parámetro de grupo es un componente de un vector de coordenadas que representa un elemento arbitrario del álgebra de Lie con respecto a alguna base. Una base, entonces, es un conjunto de generadores que son una base del álgebra de Lie en el sentido usual del espacio vectorial.

La función exponencial del álgebra de Lie al grupo de Lie proporciona una correspondencia biunívoca entre los vecindarios suficientemente pequeños del origen del álgebra de Lie y los vecindarios del elemento identidad del grupo de Lie. En el caso del grupo de Lorentz, la función exponencial es simplemente la matriz exponencial . Globalmente, la función exponencial no es biunívoca, pero en el caso del grupo de Lorentz, es sobreyectiva (sobreyectiva). Por lo tanto, cualquier elemento del grupo en el componente conexo de la identidad puede expresarse como una exponencial de un elemento del álgebra de Lie. $${\displaystyle \exp \,:\,{\mathfrak {so}}(3,1)\to \mathrm {SO} (3,1),}$$

Transformaciones inadecuadas

Las transformaciones de Lorentz también incluyen la inversión de paridad , que niega todas las coordenadas espaciales únicamente, y la inversión temporal , que niega únicamente la coordenada temporal, porque estas transformaciones dejan invariante el intervalo espacio-temporal. Aquí I es la matriz identidad 3d . Ambas son simétricas, son sus propias inversas (véase involución (matemáticas) ), y cada una tiene determinante −1. Esta última propiedad las convierte en transformaciones impropias. $${\displaystyle P={\begin{bmatrix}1&0\\0&-\mathbf {I} \end{bmatrix}}}$$ $${\displaystyle T={\begin{bmatrix}-1&0\\0&\mathbf {I} \end{bmatrix}}}$$

Si Λ es una transformación de Lorentz ortócrona propia, entonces T Λ es anticrónica impropia, P Λ es ortócrona impropia y TP Λ = PT Λ es anticrónica propia.

Grupo de Lorentz no homogéneo

No se han tenido en cuenta otras dos simetrías del espacio-tiempo. Para que el intervalo del espacio-tiempo sea invariante, se puede demostrar ^[19] que es necesario y suficiente que la transformación de coordenadas sea de la forma donde C es una columna constante que contiene traslaciones en el tiempo y el espacio. Si C ≠ 0, se trata de una transformación de Lorentz no homogénea o transformación de Poincaré . ^{[20] [21]} Si C = 0, se trata de una transformación de Lorentz homogénea . Las transformaciones de Poincaré no se tratan más en este artículo. $${\displaystyle X'=\Lambda X+C}$$

Formulación tensorial

Vectores contravariantes

Escribir la transformación matricial general de coordenadas como ecuación matricial permite la transformación de otras cantidades físicas que no se pueden expresar como cuatrivectores; por ejemplo, tensores o espinores de cualquier orden en el espacio-tiempo 4d, que se definirán. En la notación de índice tensorial correspondiente , la expresión matricial anterior es $${\displaystyle {\begin{bmatrix}{x'}^{0}\\{x'}^{1}\\{x'}^{2}\\{x'}^{3}\end{bmatrix}}={\begin{bmatrix}{\Lambda ^{0}}_{0}&{\Lambda ^{0}}_{1}&{\Lambda ^{0}}_{2}&{\Lambda ^{0}}_{3}{\vphantom {{x'}^{0}}}\\{\Lambda ^{1}}_{0}&{\Lambda ^{1}}_{1}&{\Lambda ^{1}}_{2}&{\Lambda ^{1}}_{3}{\vphantom {{x'}^{0}}}\\{\Lambda ^{2}}_{0}&{\Lambda ^{2}}_{1}&{\Lambda ^{2}}_{2}&{\Lambda ^{2}}_{3}{\vphantom {{x'}^{0}}}\\{\Lambda ^{3}}_{0}&{\Lambda ^{3}}_{1}&{\Lambda ^{3}}_{2}&{\Lambda ^{3}}_{3}{\vphantom {{x'}^{0}}}\\\end{bmatrix}}{\begin{bmatrix}x^{0}{\vphantom {{x'}^{0}}}\\x^{1}{\vphantom {{x'}^{0}}}\\x^{2}{\vphantom {{x'}^{0}}}\\x^{3}{\vphantom {{x'}^{0}}}\end{bmatrix}}}$$ $${\displaystyle {x'}^{\nu }={\Lambda ^{\nu }}_{\mu }x^{\mu },}$$

donde los índices inferior y superior etiquetan los componentes covariantes y contravariantes respectivamente, ^[22] y se aplica la convención de suma . Es una convención estándar utilizar índices griegos que toman el valor 0 para los componentes de tiempo y 1, 2, 3 para los componentes espaciales, mientras que los índices latinos simplemente toman los valores 1, 2, 3 para los componentes espaciales (lo opuesto para Landau y Lifshitz). Nótese que el primer índice (leyendo de izquierda a derecha) corresponde en la notación matricial a un índice de fila . El segundo índice corresponde al índice de columna.

La matriz de transformación es universal para todos los cuatro vectores , no solo para las coordenadas del espacio-tiempo de cuatro dimensiones. Si A es cualquier vector de cuatro dimensiones, entonces en la notación de índice tensorial $${\displaystyle {A'}^{\nu }={\Lambda ^{\nu }}_{\mu }A^{\mu }\,.}$$

Alternativamente, se escribe en donde los índices primos denotan los índices de A en el marco primo. Para un objeto general de n componentes se puede escribir donde Π es la representación apropiada del grupo de Lorentz , una matriz n × n para cada Λ . En este caso, los índices no deben considerarse como índices de espacio-tiempo (a veces llamados índices de Lorentz), y van de 1 a n . Por ejemplo, si X es un bispinor , entonces los índices se llaman índices de Dirac . $${\displaystyle A^{\nu '}={\Lambda ^{\nu '}}_{\mu }A^{\mu }\,.}$$ $${\displaystyle {X'}^{\alpha }={\Pi (\Lambda )^{\alpha }}_{\beta }X^{\beta }\,,}$$

Vectores covariantes

También hay magnitudes vectoriales con índices covariantes. Generalmente se obtienen a partir de sus objetos correspondientes con índices contravariantes mediante la operación de bajar un índice ; p. ej., donde η es el tensor métrico . (El artículo vinculado también proporciona más información sobre lo que realmente es matemáticamente la operación de subir y bajar índices). La inversa de esta transformación está dada por donde, cuando se ven como matrices, η ^μν es la inversa de η _μν . Como sucede, η ^μν = η _μν . Esto se conoce como subir un índice . Para transformar un vector covariante A _μ , primero se eleva su índice, luego se transforma de acuerdo con la misma regla que para los 4 -vectores contravariantes, luego finalmente se baja el índice; $${\displaystyle x_{\nu }=\eta _{\mu \nu }x^{\mu },}$$ $${\displaystyle x^{\mu }=\eta ^{\mu \nu }x_{\nu },}$$ $${\displaystyle {A'}_{\nu }=\eta _{\rho \nu }{\Lambda ^{\rho }}_{\sigma }\eta ^{\mu \sigma }A_{\mu }.}$$

Pero $${\displaystyle \eta _{\rho \nu }{\Lambda ^{\rho }}_{\sigma }\eta ^{\mu \sigma }={\left(\Lambda ^{-1}\right)^{\mu }}_{\nu },}$$

Es decir, es el componente ( μ , ν ) de la transformación inversa de Lorentz. Se define (como una cuestión de notación), y en esta notación se puede escribir $${\displaystyle {\Lambda _{\nu }}^{\mu }\equiv {\left(\Lambda ^{-1}\right)^{\mu }}_{\nu },}$$ $${\displaystyle {A'}_{\nu }={\Lambda _{\nu }}^{\mu }A_{\mu }.}$$

Ahora, una sutileza. La suma implícita en el lado derecho de se ejecuta sobre un índice de fila de la matriz que representa Λ ⁻¹ . Por lo tanto, en términos de matrices, esta transformación debe considerarse como la transpuesta inversa de Λ que actúa sobre el vector columna A _μ . Es decir, en notación matricial pura, $${\displaystyle {A'}_{\nu }={\Lambda _{\nu }}^{\mu }A_{\mu }={\left(\Lambda ^{-1}\right)^{\mu }}_{\nu }A_{\mu }}$$ $${\displaystyle A'=\left(\Lambda ^{-1}\right)^{\mathrm {T} }A.}$$

Esto significa exactamente que los vectores covariantes (considerados como matrices columna) se transforman de acuerdo con la representación dual de la representación estándar del grupo de Lorentz. Esta noción se generaliza a representaciones generales, simplemente reemplazando Λ por Π(Λ) .

Tensores

Si A y B son operadores lineales en espacios vectoriales U y V , entonces se puede definir un operador lineal A ⊗ B en el producto tensorial de U y V , denotado U ⊗ V de acuerdo con ^[23]

${\displaystyle (A\otimes B)(u\otimes v)=Au\otimes Bv,\qquad u\in U,v\in V,u\otimes v\in U\otimes V.}$               (T1)

De esto se desprende inmediatamente que si u y v son cuatrivectores en V , entonces u ⊗ v ∈ T ₂ V ≡ V ⊗ V se transforma como

${\displaystyle u\otimes v\rightarrow \Lambda u\otimes \Lambda v={\Lambda ^{\mu }}_{\nu }u^{\nu }\otimes {\Lambda ^{\rho }}_{\sigma }v^{\sigma }={\Lambda ^{\mu }}_{\nu }{\Lambda ^{\rho }}_{\sigma }u^{\nu }\otimes v^{\sigma }\equiv {\Lambda ^{\mu }}_{\nu }{\Lambda ^{\rho }}_{\sigma }w^{\nu \sigma }.}$               (T2)

El segundo paso utiliza la bilinealidad del producto tensorial y el último paso define un tensor de 2 componentes, o mejor dicho, simplemente cambia el nombre del tensor a u ⊗ v .

Estas observaciones se generalizan de manera obvia a más factores, y utilizando el hecho de que un tensor general en un espacio vectorial V puede escribirse como una suma de un coeficiente (¡componente!) por productos tensoriales de vectores base y covectores base, se llega a la ley de transformación para cualquier cantidad tensorial T . Está dada por ^[24]

${\displaystyle T_{\theta '\iota '\cdots \kappa '}^{\alpha '\beta '\cdots \zeta '}={\Lambda ^{\alpha '}}_{\mu }{\Lambda ^{\beta '}}_{\nu }\cdots {\Lambda ^{\zeta '}}_{\rho }{\Lambda _{\theta '}}^{\sigma }{\Lambda _{\iota '}}^{\upsilon }\cdots {\Lambda _{\kappa '}}^{\zeta }T_{\sigma \upsilon \cdots \zeta }^{\mu \nu \cdots \rho },}$               (T3)

donde Λ _χ′ ^ψ se define anteriormente. Esta forma puede reducirse generalmente a la forma para objetos generales de n componentes dada anteriormente con una sola matriz ( Π(Λ) ) que opera sobre vectores columna. Esta última forma es a veces preferida; por ejemplo, para el tensor de campo electromagnético.

Transformación del campo electromagnético

Impulso de Lorentz de una carga eléctrica, la carga está en reposo en un marco o en el otro.

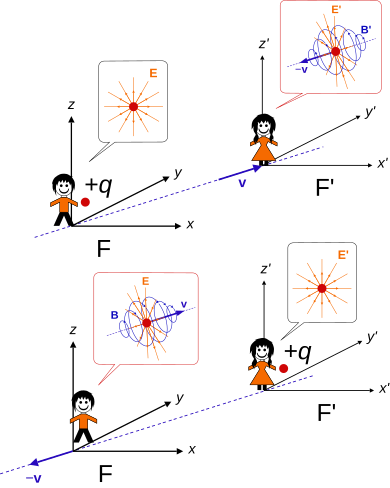
Las transformaciones de Lorentz también se pueden utilizar para ilustrar que el campo magnético B y el campo eléctrico E son simplemente aspectos diferentes de la misma fuerza: la fuerza electromagnética , como consecuencia del movimiento relativo entre cargas eléctricas y observadores. ^[25] El hecho de que el campo electromagnético muestra efectos relativistas se hace evidente al llevar a cabo un simple experimento mental. ^[26]

• Un observador mide una carga en reposo en el marco F. El observador detectará un campo eléctrico estático. Como la carga está estacionaria en este marco, no hay corriente eléctrica, por lo que el observador no observa ningún campo magnético.
• El otro observador en el sistema de referencia F′ se mueve a una velocidad v con respecto a F y a la carga. Este observador ve un campo eléctrico diferente porque la carga se mueve a una velocidad − v en su sistema de referencia en reposo. El movimiento de la carga corresponde a una corriente eléctrica y, por lo tanto, el observador en el sistema de referencia F′ también ve un campo magnético.

Los campos eléctricos y magnéticos se transforman de manera diferente desde el espacio y el tiempo, pero exactamente de la misma manera que el momento angular relativista y el vector de impulso.

El tensor de intensidad del campo electromagnético se da en unidades del SI . En relatividad, el sistema de unidades gaussiano se prefiere a menudo a las unidades del SI, incluso en textos cuya elección principal de unidades son las unidades del SI, porque en él el campo eléctrico E y la inducción magnética B tienen las mismas unidades, lo que hace que la apariencia del tensor del campo electromagnético sea más natural. ^[27] Considere un impulso de Lorentz en la dirección x . Se da por ^[28] donde el tensor de campo se muestra uno al lado del otro para la referencia más fácil posible en las manipulaciones a continuación. $${\displaystyle F^{\mu \nu }={\begin{bmatrix}0&-{\frac {1}{c}}E_{x}&-{\frac {1}{c}}E_{y}&-{\frac {1}{c}}E_{z}\\{\frac {1}{c}}E_{x}&0&-B_{z}&B_{y}\\{\frac {1}{c}}E_{y}&B_{z}&0&-B_{x}\\{\frac {1}{c}}E_{z}&-B_{y}&B_{x}&0\end{bmatrix}}{\text{(SI units, signature }}(+,-,-,-){\text{)}}.}$$ $${\displaystyle {\Lambda ^{\mu }}_{\nu }={\begin{bmatrix}\gamma &-\gamma \beta &0&0\\-\gamma \beta &\gamma &0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}},\qquad F^{\mu \nu }={\begin{bmatrix}0&E_{x}&E_{y}&E_{z}\\-E_{x}&0&B_{z}&-B_{y}\\-E_{y}&-B_{z}&0&B_{x}\\-E_{z}&B_{y}&-B_{x}&0\end{bmatrix}}{\text{(Gaussian units, signature }}(-,+,+,+){\text{)}},}$$

La ley general de transformación (T3) se convierte en $${\displaystyle F^{\mu '\nu '}={\Lambda ^{\mu '}}_{\mu }{\Lambda ^{\nu '}}_{\nu }F^{\mu \nu }.}$$

Para el campo magnético se obtiene $${\displaystyle {\begin{aligned}B_{x'}&=F^{2'3'}={\Lambda ^{2}}_{\mu }{\Lambda ^{3}}_{\nu }F^{\mu \nu }={\Lambda ^{2}}_{2}{\Lambda ^{3}}_{3}F^{23}=1\times 1\times B_{x}\\&=B_{x},\\B_{y'}&=F^{3'1'}={\Lambda ^{3}}_{\mu }{\Lambda ^{1}}_{\nu }F^{\mu \nu }={\Lambda ^{3}}_{3}{\Lambda ^{1}}_{\nu }F^{3\nu }={\Lambda ^{3}}_{3}{\Lambda ^{1}}_{0}F^{30}+{\Lambda ^{3}}_{3}{\Lambda ^{1}}_{1}F^{31}\\&=1\times (-\beta \gamma )(-E_{z})+1\times \gamma B_{y}=\gamma B_{y}+\beta \gamma E_{z}\\&=\gamma \left(\mathbf {B} -{\boldsymbol {\beta }}\times \mathbf {E} \right)_{y}\\B_{z'}&=F^{1'2'}={\Lambda ^{1}}_{\mu }{\Lambda ^{2}}_{\nu }F^{\mu \nu }={\Lambda ^{1}}_{\mu }{\Lambda ^{2}}_{2}F^{\mu 2}={\Lambda ^{1}}_{0}{\Lambda ^{2}}_{2}F^{02}+{\Lambda ^{1}}_{1}{\Lambda ^{2}}_{2}F^{12}\\&=(-\gamma \beta )\times 1\times E_{y}+\gamma \times 1\times B_{z}=\gamma B_{z}-\beta \gamma E_{y}\\&=\gamma \left(\mathbf {B} -{\boldsymbol {\beta }}\times \mathbf {E} \right)_{z}\end{aligned}}}$$

Para los resultados del campo eléctrico $${\displaystyle {\begin{aligned}E_{x'}&=F^{0'1'}={\Lambda ^{0}}_{\mu }{\Lambda ^{1}}_{\nu }F^{\mu \nu }={\Lambda ^{0}}_{1}{\Lambda ^{1}}_{0}F^{10}+{\Lambda ^{0}}_{0}{\Lambda ^{1}}_{1}F^{01}\\&=(-\gamma \beta )(-\gamma \beta )(-E_{x})+\gamma \gamma E_{x}=-\gamma ^{2}\beta ^{2}(E_{x})+\gamma ^{2}E_{x}=E_{x}(1-\beta ^{2})\gamma ^{2}\\&=E_{x},\\E_{y'}&=F^{0'2'}={\Lambda ^{0}}_{\mu }{\Lambda ^{2}}_{\nu }F^{\mu \nu }={\Lambda ^{0}}_{\mu }{\Lambda ^{2}}_{2}F^{\mu 2}={\Lambda ^{0}}_{0}{\Lambda ^{2}}_{2}F^{02}+{\Lambda ^{0}}_{1}{\Lambda ^{2}}_{2}F^{12}\\&=\gamma \times 1\times E_{y}+(-\beta \gamma )\times 1\times B_{z}=\gamma E_{y}-\beta \gamma B_{z}\\&=\gamma \left(\mathbf {E} +{\boldsymbol {\beta }}\times \mathbf {B} \right)_{y}\\E_{z'}&=F^{0'3'}={\Lambda ^{0}}_{\mu }{\Lambda ^{3}}_{\nu }F^{\mu \nu }={\Lambda ^{0}}_{\mu }{\Lambda ^{3}}_{3}F^{\mu 3}={\Lambda ^{0}}_{0}{\Lambda ^{3}}_{3}F^{03}+{\Lambda ^{0}}_{1}{\Lambda ^{3}}_{3}F^{13}\\&=\gamma \times 1\times E_{z}-\beta \gamma \times 1\times (-B_{y})=\gamma E_{z}+\beta \gamma B_{y}\\&=\gamma \left(\mathbf {E} +{\boldsymbol {\beta }}\times \mathbf {B} \right)_{z}.\end{aligned}}}$$

Aquí, se utiliza β = ( β , 0, 0) . Estos resultados se pueden resumir por y son independientes de la firma métrica. Para las unidades del SI, sustituya E → E ⁄ c . Misner, Thorne y Wheeler (1973) se refieren a esta última forma como la vista 3 + 1 en oposición a la vista geométrica representada por la expresión tensorial y destacan la facilidad con la que se pueden obtener y comprender resultados que son difíciles de lograr utilizando la vista 3 + 1. Solo los objetos que tienen propiedades de transformación de Lorentz bien definidas (de hecho, bajo cualquier transformación de coordenadas suave) son objetos geométricos. En la vista geométrica, el campo electromagnético es un objeto geométrico de seis dimensiones en el espacio-tiempo en oposición a dos campos de 3 vectores interdependientes, pero separados, en el espacio y el tiempo . Los campos E (solo) y B (solo) no tienen propiedades de transformación de Lorentz bien definidas. Los fundamentos matemáticos son las ecuaciones (T1) y (T2) que producen inmediatamente (T3) . Cabe señalar que los tensores con y sin prima se refieren al mismo evento en el espacio-tiempo . Por lo tanto, la ecuación completa con dependencia del espacio-tiempo es $${\displaystyle {\begin{aligned}\mathbf {E} _{\parallel '}&=\mathbf {E} _{\parallel }\\\mathbf {B} _{\parallel '}&=\mathbf {B} _{\parallel }\\\mathbf {E} _{\bot '}&=\gamma \left(\mathbf {E} _{\bot }+{\boldsymbol {\beta }}\times \mathbf {B} _{\bot }\right)=\gamma \left(\mathbf {E} +{\boldsymbol {\beta }}\times \mathbf {B} \right)_{\bot },\\\mathbf {B} _{\bot '}&=\gamma \left(\mathbf {B} _{\bot }-{\boldsymbol {\beta }}\times \mathbf {E} _{\bot }\right)=\gamma \left(\mathbf {B} -{\boldsymbol {\beta }}\times \mathbf {E} \right)_{\bot },\end{aligned}}}$$ $${\displaystyle F^{\mu '\nu '}={\Lambda ^{\mu '}}_{\mu }{\Lambda ^{\nu '}}_{\nu }F^{\mu \nu },}$$ $${\displaystyle F^{\mu '\nu '}\left(x'\right)={\Lambda ^{\mu '}}_{\mu }{\Lambda ^{\nu '}}_{\nu }F^{\mu \nu }\left(\Lambda ^{-1}x'\right)={\Lambda ^{\mu '}}_{\mu }{\Lambda ^{\nu '}}_{\nu }F^{\mu \nu }(x).}$$

La contracción de la longitud tiene un efecto sobre la densidad de carga ρ y la densidad de corriente J , y la dilatación del tiempo tiene un efecto sobre la tasa de flujo de carga (corriente), por lo que las distribuciones de carga y corriente deben transformarse de una manera relacionada bajo un impulso. Resulta que se transforman exactamente como los cuatro vectores de espacio-tiempo y energía-momento, $${\displaystyle {\begin{aligned}\mathbf {j} '&=\mathbf {j} -\gamma \rho v\mathbf {n} +\left(\gamma -1\right)(\mathbf {j} \cdot \mathbf {n} )\mathbf {n} \\\rho '&=\gamma \left(\rho -\mathbf {j} \cdot {\frac {v\mathbf {n} }{c^{2}}}\right),\end{aligned}}}$$

o, en la visión geométrica más simple, $${\displaystyle j^{\mu '}={\Lambda ^{\mu '}}_{\mu }j^{\mu }.}$$

La densidad de carga se transforma como el componente temporal de un cuatrivector. Es un escalar rotacional. La densidad de corriente es un 3-vector.

Las ecuaciones de Maxwell son invariantes bajo las transformaciones de Lorentz.

Espinores

La ecuación (T1) se mantiene sin modificaciones para cualquier representación del grupo de Lorentz, incluida la representación bispinorial . En (T2) uno simplemente reemplaza todas las ocurrencias de Λ por la representación bispinorial Π(Λ) ,

${\displaystyle {\begin{aligned}u\otimes v\rightarrow \Pi (\Lambda )u\otimes \Pi (\Lambda )v&={\Pi (\Lambda )^{\alpha }}_{\beta }u^{\beta }\otimes {\Pi (\Lambda )^{\rho }}_{\sigma }v^{\sigma }\\&={\Pi (\Lambda )^{\alpha }}_{\beta }{\Pi (\Lambda )^{\rho }}_{\sigma }u^{\beta }\otimes v^{\sigma }\\&\equiv {\Pi (\Lambda )^{\alpha }}_{\beta }{\Pi (\Lambda )^{\rho }}_{\sigma }w^{\beta \sigma }\end{aligned}}}$               (T4)

La ecuación anterior podría, por ejemplo, ser la transformación de un estado en el espacio de Fock que describe dos electrones libres.

Transformación de campos generales

Un estado multipartícula general no interactuante (estado de espacio de Fock) en la teoría cuántica de campos se transforma de acuerdo con la regla ^[29]

donde W (Λ, p ) es el pequeño grupo de Wigner ^[30] y D ^{( j )} es la representación (2 j + 1) -dimensional de SO(3) .

Véase también

• Cálculo de Ricci
• Campo electromagnético
• Transformación galileana
• Rotación hiperbólica
• Grupo de Lorentz
• Teoría de la representación del grupo de Lorentz
• Principio de relatividad
• Fórmula de adición de velocidad
• Álgebra del espacio físico
• Aberración relativista
• Transformación de Prandtl-Glauert
• Número complejo dividido
• Espacio girovectorial

Notas al pie

1. Se puede imaginar que en cada sistema inercial hay observadores ubicados en el espacio, cada uno con un reloj sincronizado y en reposo en el sistema inercial particular. Estos observadores informan a una oficina central, donde se recogen todos los informes. Cuando se habla de un observador particular , se hace referencia a alguien que tiene, al menos en principio, una copia de este informe. Véase, por ejemplo, Sard (1970).
2. Los requisitos separados de las tres ecuaciones conducen a tres grupos diferentes. La segunda ecuación se satisface para las traslaciones del espacio-tiempo además de las transformaciones de Lorentz que conducen al grupo de Poincaré o al grupo de Lorentz no homogéneo . La primera ecuación (o la segunda restringida a la separación similar a la luz) conduce a un grupo aún más grande, el grupo conforme del espacio-tiempo.
3. Los grupos O(3, 1) y O(1, 3) son isomorfos. Se cree ampliamente que la elección entre las dos firmas métricas no tiene relevancia física, aunque algunos objetos relacionados con O(3, 1) y O(1, 3) respectivamente, por ejemplo, las álgebras de Clifford correspondientes a las diferentes firmas de la forma bilineal asociada a los dos grupos, no son isomorfos.
4. Para dos matrices cuadradas A y B , det( AB ) = det( A )det( B )
5. Explícitamente, $${\displaystyle {\boldsymbol {\zeta }}\cdot \mathbf {K} =\zeta _{x}K_{x}+\zeta _{y}K_{y}+\zeta _{z}K_{z}}$$ $${\displaystyle {\boldsymbol {\theta }}\cdot \mathbf {J} =\theta _{x}J_{x}+\theta _{y}J_{y}+\theta _{z}J_{z}}$$
6. En la mecánica cuántica , la mecánica cuántica relativista y la teoría cuántica de campos , se utiliza una convención diferente para estas matrices: los lados derechos se multiplican todos por un factor de la unidad imaginaria i = √ −1 .
7. Hasta ahora, el término "vector" se ha referido exclusivamente a " vector euclidiano ", como por ejemplo la posición r , la velocidad v , etc. El término "vector" se aplica de forma mucho más amplia que los vectores euclidianos, los vectores fila o columna, etc., véase álgebra lineal y espacio vectorial para más detalles. Los generadores de un grupo de Lie también forman un espacio vectorial sobre un cuerpo de números (por ejemplo, números reales , números complejos ), ya que una combinación lineal de los generadores también es un generador. Simplemente viven en un espacio diferente al de los vectores de posición en el espacio 3D ordinario.
8. el espacio de posición 3D ordinario , el vector de posición r = x e _x + y e _y + z e _z se expresa como una combinación lineal de los vectores unitarios cartesianos e _x , e _y , e _z que forman una base, y las coordenadas cartesianas x, y, z son coordenadas con respecto a esta base.

Notas

1. Rao, KN Srinivasa (1988). Los grupos de rotación y de Lorentz y sus representaciones para los físicos (edición ilustrada). John Wiley & Sons. pág. 213. ISBN 978-0-470-21044-4.Ecuación 6-3.24, página 210
2. Forshaw y Smith 2009
3. Cottingham y Greenwood 2007, pág. 21
4. Lorentz 1904
5. O'Connor y Robertson 1996
6. Marrón 2003
7. Rothman 2006, págs. 112 y siguientes.
8. Darrigol 2005, págs. 1–22
9. Macrossan 1986, págs. 232–34
10. La referencia se encuentra en el siguiente artículo: Poincaré 1905, pp. 1504–1508
11. Einstein 1905, págs. 891–921
12. Young & Freedman 2008
13. Forshaw y Smith 2009
14. Andrew M. Steane (2012). Relativity Made Relatively Easy (edición ilustrada). OUP Oxford. pág. 124. ISBN 978-0-19-966286-9.Extracto de la página 124
15. Einstein 1916
16. Barut 1964, pág. 18-19
17. Chaichian y Hagedorn 1997, pág. 239
18. Furry, WH (1 de noviembre de 1955). "Transformación de Lorentz y precesión de Thomas". Revista estadounidense de física . 23 (8): 517–525. Código Bibliográfico :1955AmJPh..23..517F. doi :10.1119/1.1934085. ISSN  0002-9505.
19. Weinberg 1972
20. Weinberg 2005, págs. 55-58
21. Ohlsson 2011, págs. 3-9
22. Dennery y Krzywicki 2012, pág. 138
23. Hall 2003, Capítulo 4
24. Carroll 2004, pág. 22
25. Grant y Phillips 2008
26. Griffiths 2007
27. Jackson 1975, p.  ^{[ página necesaria ]}
28. Misner, Thorne y Wheeler 1973
29. Weinberg 2002, Capítulo 3
30. "INSPIRE". inspirehep.net . Consultado el 4 de septiembre de 2024 .

Referencias

Sitios web

• O'Connor, John J.; Robertson, Edmund F. (1996), Una historia de la relatividad especial
• Brown, Harvey R. (2003), Michelson, FitzGerald y Lorentz: los orígenes de la relatividad revisitados

Papeles

• Cushing, JT (1967). "Transformaciones vectoriales de Lorentz". American Journal of Physics . 35 (9): 858–862. Código Bibliográfico :1967AmJPh..35..858C. doi :10.1119/1.1974267.
• Macfarlane, AJ (1962). "Sobre el grupo restringido de Lorentz y grupos homomórficamente relacionados con él". Journal of Mathematical Physics . 3 (6): 1116–1129. Bibcode :1962JMP.....3.1116M. doi :10.1063/1.1703854. hdl : 2027/mdp.39015095220474 .
• Rothman, Tony (2006), "Perdido en la sombra de Einstein" (PDF) , American Scientist , 94 (2): 112f
• Darrigol, Olivier (2005), "La Génesis de la teoría de la relatividad" (PDF) , Séminaire Poincaré , 1 : 1–22, Bibcode :2006eins.book....1D, doi :10.1007/3-7643-7436- 5_1, ISBN 978-3-7643-7435-8
• Macrossan, Michael N. (1986), "Una nota sobre la relatividad antes de Einstein", Br. J. Philos. Sci. , 37 (2): 232–34, CiteSeerX  10.1.1.679.5898 , doi :10.1093/bjps/37.2.232, archivado desde el original el 29 de octubre de 2013 , consultado el 2 de abril de 2007
• Poincaré, Henri (1905), "Sobre la dinámica del electrón"  , Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences , 140 : 1504-1508
• Einstein, Albert (1905), "Zur Elektrodynamik bewegter Körper" (PDF) , Annalen der Physik , 322 (10): 891–921, Bibcode :1905AnP...322..891E, doi : 10.1002/andp.19053221004. Véase también: Traducción al inglés.
• Lorentz, Hendrik Antoon (1904). "Fenómenos electromagnéticos en un sistema que se mueve a una velocidad menor que la de la luz"  . Actas de la Real Academia de las Artes y las Ciencias de los Países Bajos . 6 : 809–831.
• Einstein, A. (1916). Relatividad: teoría especial y general . Consultado el 23 de enero de 2012 . Einstein, A. (1916). Relatividad: teoría especial y general. Nueva York: Three Rivers Press (publicado en 1995). ISBN 978-0-517-88441-6– vía Archivo de Referencia Albert Einstein.
• Ungar, AA (1988). "Rotación de Thomas y parametrización del grupo de transformación de Lorentz". Fundamentos de Física Letters . 1 (1): 55–89. Bibcode :1988FoPhL...1...57U. doi :10.1007/BF00661317. ISSN  0894-9875. S2CID  121240925.ecuación (55).
• Ungar, AA (1989). "La paradoja de la composición de velocidad relativista y la rotación de Thomas". Fundamentos de la Física . 19 (11): 1385–1396. Bibcode :1989FoPh...19.1385U. doi :10.1007/BF00732759. S2CID  55561589.
• Ungar, AA (2000). "El principio relativista de reciprocidad de velocidad compuesta". Fundamentos de la Física . 30 (2): 331–342. Bibcode :2000FoPh...30..331U. CiteSeerX  10.1.1.35.1131 . doi :10.1023/A:1003653302643. S2CID  118634052.
• Mocanu, CI (1986). "Algunas dificultades en el marco de la electrodinámica relativista". Archiv für Elektrotechnik . 69 (2): 97–110. doi :10.1007/bf01574845. S2CID  123543303.
• Mocanu, CI (1992). "Sobre la paradoja de la composición de velocidad relativista y la rotación de Thomas". Fundamentos de la Física . 5 (5): 443–456. Bibcode :1992FoPhL...5..443M. doi :10.1007/bf00690425. S2CID  122472788.
• Weinberg, S. (2002). La teoría cuántica de campos, vol. I. Cambridge University Press . ISBN 978-0-521-55001-7.

Libros

• Barut, Asim Orhan (1964). Electrodinámica y teoría clásica de campos y partículas. Macmillan. ISBN 978-0-486-64038-9.
• Dennery, Philippe; Krzywicki, André (2012). Matemáticas para físicos. Courier Corporation. ISBN 978-0-486-15712-2.
• Cottingham, WN; Greenwood, DA (2007). Introducción al modelo estándar de física de partículas (2.ª ed.). Cambridge University Press. ISBN 978-1-139-46221-1.
• Young, HD; Freedman, RA (2008). Física universitaria: con física moderna (12.ª ed.). Pearson Addison-Wesley. ISBN 978-0-321-50130-1.
• Halpern, A. (1988). 3000 Problemas Resueltos de Física . Serie Schaum. Mc Graw Hill. pág. 688. ISBN 978-0-07-025734-4.
• Forshaw, JR; Smith, AG (2009). Dinámica y relatividad . Manchester Physics Series. John Wiley & Sons Ltd., págs. 124-126. ISBN 978-0-470-01460-8.
• Wheeler, JA ; Taylor, E. F (1971). Física del espacio-tiempo . Freeman. ISBN 978-0-7167-0336-5.
• Wheeler, JA ; Thorne, KS ; Misner, CW (1973). Gravitación . Freeman. ISBN 978-0-7167-0344-0.
• Carroll, SM (2004). Espacio-tiempo y geometría: una introducción a la relatividad general (edición ilustrada). Addison Wesley. pág. 22. ISBN 978-0-8053-8732-2.
• Grant, IS; Phillips, WR (2008). "14". Electromagnetismo . Manchester Physics (2.ª ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
• Griffiths, DJ (2007). Introducción a la electrodinámica (3.ª ed.). Pearson Education, Dorling Kindersley. ISBN 978-81-7758-293-2.
• Hall, Brian C. (2003). Grupos de Lie, álgebras de Lie y representaciones: una introducción elemental . Springer . ISBN 978-0-387-40122-5.
• Weinberg, Steven (1972). Gravitación y cosmología: principios y aplicaciones de la teoría general de la relatividad. Wiley. ISBN 978-0-471-92567-5.
• Weinberg, S. (2008), Cosmología , Wiley, ISBN 978-0-19-852682-7
• Weinberg, S. (2005), La teoría cuántica de campos (3 vol.) , vol. 1, Cambridge University Press, ISBN 978-0-521-67053-1
• Ohlsson, T. (2011), Física cuántica relativista , Cambridge University Press, ISBN 978-0-521-76726-2
• Goldstein, H. (1980) [1950]. Mecánica clásica (2.ª ed.). Reading MA: Addison-Wesley . ISBN 978-0-201-02918-5.
• Jackson, JD (1975) [1962]. "Capítulo 11". Electrodinámica clásica (2.ª ed.). John Wiley & Sons . pp. 542–545. ISBN 978-0-471-43132-9.
• Landau, LD ; Lifshitz, EM (2002) [1939]. La teoría clásica de campos . Curso de física teórica . Vol. 2 (4.ª ed.). Butterworth–Heinemann . págs. 9–12. ISBN 0-7506-2768-9.
• Feynman, RP ; Leighton, RB ; Sands, M. (1977) [1963]. "15". Las conferencias Feynman sobre física . Vol. 1. Addison Wesley. ISBN 978-0-201-02117-2.
• Feynman, RP ; Leighton, RB ; Sands, M. (1977) [1964]. "13". Las conferencias Feynman sobre física . Vol. 2. Addison Wesley. ISBN 978-0-201-02117-2.
• Misner, Charles W .; Thorne, Kip S .; Wheeler, John Archibald (1973). Gravitación . San Francisco: WH Freeman . ISBN. 978-0-7167-0344-0.
• Rindler, W. (2006) [2001]. "Capítulo 9". Relatividad especial, general y cosmológica (2.ª ed.). Dallas: Oxford University Press . ISBN 978-0-19-856732-5.
• Ryder, LH (1996) [1985]. Teoría cuántica de campos (2.ª ed.). Cambridge: Cambridge University Press . ISBN 978-0521478144.
• Sard, RD (1970). Mecánica relativista: relatividad especial y dinámica clásica de partículas . Nueva York: WA Benjamin. ISBN 978-0805384918.
• Sexl, RU; Urbantke, HK (2001) [1992]. Relatividad, grupos de partículas. Relatividad especial y simetría relativista en física de campos y partículas. Springer. ISBN 978-3211834435.
• Gourgoulhon, Eric (2013). Relatividad especial en marcos generales: de las partículas a la astrofísica. Springer. pág. 213. ISBN 978-3-642-37276-6.
• Chaichian, Masud; Hagedorn, Rolf (1997). Simetría en mecánica cuántica: del momento angular a la supersimetría. IoP. p. 239. ISBN 978-0-7503-0408-5.
• Landau, LD ; Lifshitz, EM (2002) [1939]. La teoría clásica de campos . Curso de física teórica. Vol. 2 (4.ª ed.). Butterworth–Heinemann . ISBN 0-7506-2768-9.

Lectura adicional

• Ernst, A.; Hsu, J.-P. (2001), "Primera propuesta de la velocidad universal de la luz por Voigt 1887" (PDF) , Chinese Journal of Physics , 39 (3): 211–230, Bibcode :2001ChJPh..39..211E, archivado desde el original (PDF) el 2011-07-16
• Thornton, Stephen T.; Marion, Jerry B. (2004), Dinámica clásica de partículas y sistemas (5.ª ed.), Belmont, [CA.]: Brooks/Cole, págs. 546–579, ISBN 978-0-534-40896-1
• Voigt, Woldemar (1887), "Über das Doppler'sche princip", Nachrichten von der Königlicher Gesellschaft den Wissenschaft zu Göttingen , 2 : 41–51

Enlaces externos

• Derivación de las transformaciones de Lorentz. Esta página web contiene una derivación más detallada de la transformación de Lorentz con especial énfasis en las propiedades de grupo.
• La paradoja de la relatividad especial. Esta página web plantea un problema cuya solución es la transformación de Lorentz, que se presenta gráficamente en la página siguiente.
• Relatividad Archivado el 29 de agosto de 2011 en Wayback Machine – un capítulo de un libro de texto en línea
• Simulador de relatividad especial Warp. Un programa informático que muestra las transformaciones de Lorentz en objetos cotidianos.
• Clip de animación en YouTube que visualiza la transformación de Lorentz.
• Vídeo de MinutePhysics en YouTube que explica y visualiza la transformación de Lorentz con un diagrama mecánico de Minkowski
• Gráfico interactivo en Desmos (gráficos) que muestra las transformaciones de Lorentz con un diagrama de Minkowski virtual
• Gráfico interactivo en Desmos que muestra transformaciones de Lorentz con puntos e hipérbolas
• Marcos de Lorentz animados de John de Pillis. Animaciones Flash en línea de marcos de Galileo y Lorentz, varias paradojas, fenómenos de ondas electromagnéticas, etc.