Diagrama de Smith

Calculadora gráfica para ingenieros eléctricos

El diagrama de Smith (a veces también llamado diagrama de Smith , diagrama de Mizuhashi (水橋チャート), diagrama de Mizuhashi-Smith (水橋スミスチャート), ^{[1] [2] [3]} diagrama de Volpert-Smith ( Диаграмма Вольперта—Смита ) ^{[4] [5]} o tabla de Mizuhashi-Volpert-Smith ), es una calculadora gráfica o nomograma diseñada para ingenieros eléctricos y electrónicos especializados en ingeniería de radiofrecuencia (RF) para ayudar a resolver problemas con líneas de transmisión y circuitos coincidentes . . ^{[6] [7] [8] [9] [10]}

Fue propuesto independientemente ^{[11] [4] [12] [5] por Tōsaku Mizuhashi (}水橋東作) en 1937, ^[13] y por Amiel R. Volpert  [ru] ( Амиэ́ль Р. Во́льперт ) ^{[14] [4]} y Phillip H. Smith en 1939. ^{[15] [16]} Comenzando con un diagrama rectangular, Smith había desarrollado un gráfico de coordenadas polares especial en 1936, que, con el aporte de sus colegas Enoch B. Ferrell y James W. McRae , quienes estaban familiarizados con las aplicaciones conformes , fue reelaborado en la forma final a principios de 1937, que finalmente se publicó en enero de 1939. ^{[15] [9] [17]} Si bien Smith originalmente lo había llamado un " diagrama de línea de transmisión " ^{[15] [16]} y otros autores utilizaron por primera vez nombres como " diagrama de reflexión ", " diagrama circular de impedancia ", " diagrama de inmitancia " o " diagrama del plano Z ", ^[9] los primeros en adoptarlo en el Laboratorio de Radiación del MIT comenzaron a referirse a él simplemente como " diagrama de Smith " en la década de 1940, ^{[9] [17]} un nombre generalmente aceptado en el mundo occidental en 1950. ^{[18] [19]}

El diagrama de Smith se puede utilizar para mostrar simultáneamente múltiples parámetros, incluyendo impedancias , admitancias , coeficientes de reflexión , parámetros de dispersión , círculos de figura de ruido , contornos de ganancia constante y regiones para estabilidad incondicional . ^{[20] [21] : 93–103} El diagrama de Smith se utiliza con mayor frecuencia en o dentro de la región de radio unitario . Sin embargo, el resto sigue siendo matemáticamente relevante, utilizándose, por ejemplo, en el diseño de osciladores y análisis de estabilidad . ^{[21] : 98–101} Si bien el uso de diagramas de Smith en papel para resolver las matemáticas complejas involucradas en problemas de emparejamiento ha sido reemplazado en gran medida por métodos basados ​​en software, el diagrama de Smith sigue siendo un método muy útil para mostrar ^[22] cómo se comportan los parámetros de RF en una o más frecuencias, una alternativa al uso de información tabular . Por lo tanto, la mayoría del software de análisis de circuitos de RF incluye una opción de diagrama de Smith para la visualización de resultados y todos los instrumentos de medición de impedancia, excepto los más simples, pueden trazar los resultados medidos en una pantalla de diagrama de Smith. ^[23] ${\displaystyle S_{nn}\,}$

Un diagrama de Smith de impedancia (sin datos representados).

Descripción general

Un analizador de red ( HP 8720A) que muestra un diagrama de Smith.

El diagrama de Smith es una transformación matemática del plano complejo cartesiano bidimensional. Los números complejos con partes reales positivas se representan dentro del círculo. Aquellos con partes reales negativas se representan fuera del círculo. Si solo tratamos con impedancias con componentes resistivos no negativos, nuestro interés se centra en el área dentro del círculo. La transformación, para un diagrama de Smith de impedancias, es:

${\displaystyle \Gamma ={\frac {Z-Z_{0}}{Z+Z_{0}}}={\frac {z-1}{z+1}},}$

donde ie, la impedancia compleja, normalizada por la impedancia de referencia, . El diagrama de Smith de impedancia es entonces un diagrama de Argand de impedancias así transformadas. Las impedancias con componentes resistivos no negativos aparecerán dentro de un círculo con radio unitario; el origen corresponderá a la impedancia de referencia, . ${\displaystyle z={\frac {Z}{Z_{0}}},}$ ${\displaystyle Z,}$ ${\displaystyle Z_{0}}$ ${\displaystyle Z_{0}}$

El diagrama de Smith se traza en el plano del coeficiente de reflexión complejo en dos dimensiones y se puede escalar en impedancia normalizada (la más común), admitancia normalizada o ambas, utilizando diferentes colores para distinguirlas. Estos a menudo se conocen como diagramas de Smith Z, Y e YZ respectivamente. ^{[21] : 97} El escalado normalizado permite que el diagrama de Smith se utilice para problemas que involucran cualquier impedancia característica o del sistema que esté representada por el punto central del diagrama. La impedancia de normalización más comúnmente utilizada es 50  ohmios . Una vez que se obtiene una respuesta a través de las construcciones gráficas descritas a continuación, es sencillo convertir entre impedancia normalizada (o admitancia normalizada) y el valor no normalizado correspondiente multiplicando por la impedancia característica (admitancia). Los coeficientes de reflexión se pueden leer directamente del diagrama, ya que son parámetros sin unidades.

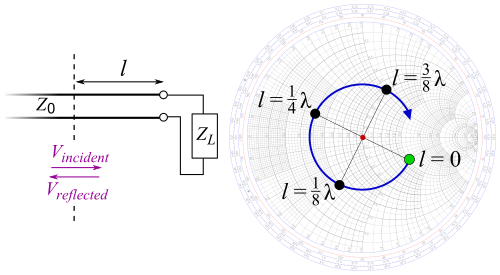
El diagrama de Smith tiene una escala alrededor de su circunferencia o periferia que está graduada en longitudes de onda y grados . La escala de longitudes de onda se utiliza en problemas de componentes distribuidos y representa la distancia medida a lo largo de la línea de transmisión conectada entre el generador o fuente y la carga hasta el punto en consideración. La escala de grados representa el ángulo del coeficiente de reflexión de voltaje en ese punto. El diagrama de Smith también se puede utilizar para problemas de análisis y emparejamiento de elementos concentrados .

El uso del diagrama de Smith y la interpretación de los resultados obtenidos mediante él requieren una buena comprensión de la teoría de circuitos de CA y de la teoría de líneas de transmisión, ambas requisitos previos para los ingenieros de RF.

Como las impedancias y admitancias cambian con la frecuencia, los problemas que utilizan el diagrama de Smith solo se pueden resolver manualmente utilizando una frecuencia a la vez, y el resultado se representa mediante un punto . Esto suele ser adecuado para aplicaciones de banda estrecha (normalmente hasta aproximadamente el 5 % al 10 % del ancho de banda ), pero para anchos de banda más amplios suele ser necesario aplicar técnicas de diagrama de Smith en más de una frecuencia en toda la banda de frecuencia operativa. Siempre que las frecuencias sean lo suficientemente cercanas, los puntos resultantes del diagrama de Smith se pueden unir mediante líneas rectas para crear un lugar geométrico .

Se puede utilizar un lugar geométrico de puntos en un diagrama de Smith que cubra un rango de frecuencias para representar visualmente:

• Qué tan capacitiva o inductiva es una carga en todo el rango de frecuencia
• Qué tan difícil es probablemente la coincidencia en varias frecuencias
• qué tan bien se adapta un componente en particular.

La precisión del diagrama de Smith se reduce para problemas que involucran un gran lugar geométrico de impedancias o admitancias, aunque la escala se puede ampliar para áreas individuales para acomodarlas.

Base matemática

Uso más básico de un diagrama de Smith de impedancia. Una onda viaja a través de una línea de transmisión de impedancia característica Z ₀ , terminada en una carga con impedancia Z _L e impedancia normalizada z = Z _L / Z ₀ . Hay una reflexión de señal con coeficiente Γ. Cada punto en el diagrama de Smith representa simultáneamente un valor de z (abajo a la izquierda) y el valor correspondiente de Γ (abajo a la derecha), relacionados por z = (1 + Γ) / (1 − Γ).

Impedancia y admitancia reales y normalizadas

Una línea de transmisión con una impedancia característica de puede considerarse universalmente como si tuviera una admitancia característica de donde ${\displaystyle Z_{0}\,}$ ${\displaystyle Y_{0}\,}$

${\displaystyle Y_{0}={\frac {1}{Z_{0}}}\,}$

Cualquier impedancia, expresada en ohmios, se puede normalizar dividiéndola por la impedancia característica, por lo que la impedancia normalizada utilizando la letra z _T minúscula viene dada por ${\displaystyle Z_{\text{T}}\,}$

${\displaystyle z_{\text{T}}={\frac {Z_{\text{T}}}{Z_{0}}}\,}$

De manera similar, para la admitancia normalizada

${\displaystyle y_{\text{T}}={\frac {Y_{\text{T}}}{Y_{0}}}\,}$

La unidad SI de impedancia es el ohmio con el símbolo de la letra griega mayúscula omega (Ω) y la unidad SI de admitancia es el siemens con el símbolo de la letra S mayúscula. La impedancia normalizada y la admitancia normalizada son adimensionales . Las impedancias y admitancias reales deben normalizarse antes de usarlas en una tabla de Smith. Una vez que se obtiene el resultado, se puede desnormalizar para obtener el resultado real.

Diagrama de Smith de impedancia normalizada

Líneas de transmisión terminadas en un circuito abierto (arriba) y un cortocircuito (abajo). Un pulso se refleja perfectamente en ambas terminaciones, pero el signo del voltaje reflejado es opuesto en los dos casos. Los puntos negros representan electrones y las flechas muestran el campo eléctrico.

Utilizando la teoría de líneas de transmisión, si una línea de transmisión termina en una impedancia ( ) que difiere de su impedancia característica ( ), se formará una onda estacionaria en la línea que comprende la resultante de las ondas incidente o hacia adelante ( ) y reflejada o invertida ( ). Utilizando la notación exponencial compleja : ${\displaystyle Z_{\text{T}}\,}$ ${\displaystyle Z_{0}\,}$ ${\displaystyle V_{\text{F}}\,}$ ${\displaystyle V_{\text{R}}\,}$

${\displaystyle V_{\text{F}}=A\exp(j\omega t)\exp(+\gamma \ell )~\,}$y

${\displaystyle V_{\text{R}}=B\exp(j\omega t)\exp(-\gamma \ell )\,}$

dónde

${\displaystyle \exp(j\omega t)\,}$es la parte temporal de la onda

${\displaystyle \exp(\pm \gamma \ell )\,}$es la parte espacial de la onda y

${\displaystyle \omega =2\pi f\,}$dónde

${\displaystyle \omega \,}$es la frecuencia angular en radianes por segundo (rad/s)

${\displaystyle f\,}$es la frecuencia en hercios (Hz)

${\displaystyle t\,}$es el tiempo en segundos (s)

${\displaystyle A\,}$y son constantes ${\displaystyle B\,}$

${\displaystyle \ell \,}$es la distancia medida a lo largo de la línea de transmisión desde la carga hacia el generador en metros (m)

También

${\displaystyle \gamma =\alpha +j\beta \,}$es la constante de propagación que tiene unidades SI radianes / metro

dónde

${\displaystyle \alpha \,}$es la constante de atenuación en nepers por metro (Np/m)

${\displaystyle \beta \,}$es la constante de fase en radianes por metro (rad/m)

El diagrama de Smith se utiliza con una frecuencia ( ) a la vez, y solo para un momento ( ) a la vez, por lo que la parte temporal de la fase ( ) es fija. En realidad, todos los términos se multiplican por esto para obtener la fase instantánea , pero es convencional y se entiende que se omite. Por lo tanto, ${\displaystyle \omega }$ ${\displaystyle t}$ ${\displaystyle \exp(j\omega t)\,}$

${\displaystyle V_{\text{F}}=A\exp(+\gamma \ell )\,}$y

${\displaystyle V_{\text{R}}=B\exp(-\gamma \ell )\,}$

donde y son respectivamente las amplitudes de voltaje directo e inverso en la carga. ${\displaystyle A\,}$ ${\displaystyle B\,}$

La variación del coeficiente de reflexión complejo con la posición a lo largo de la línea

Mirando hacia una carga a través de una longitud de línea de transmisión sin pérdidas, la impedancia cambia a medida que aumenta, siguiendo el círculo azul. (Esta impedancia se caracteriza por su coeficiente de reflexión ). El círculo azul, centrado dentro del diagrama de Smith de impedancia, a veces se denomina círculo SWR (abreviatura de relación de onda estacionaria constante ). ${\displaystyle \ell \,}$ ${\displaystyle \ell \,}$ ${\displaystyle V_{\text{reflected}}/V_{\text{incident}}}$

El coeficiente de reflexión de voltaje complejo se define como la relación entre la onda reflejada y la onda incidente (o directa). Por lo tanto, ${\displaystyle \Gamma \,}$

${\displaystyle \Gamma ={\frac {V_{\text{R}}}{V_{\text{F}}}}={\frac {B\exp(-\gamma \ell )}{A\exp(+\gamma \ell )}}=C\exp(-2\gamma \ell )\,}$

donde C también es una constante.

Para una línea de transmisión uniforme (en la que es constante), el coeficiente de reflexión complejo de una onda estacionaria varía según la posición en la línea. Si la línea tiene pérdidas ( no es cero), esto se representa en el diagrama de Smith mediante una trayectoria en espiral . Sin embargo, en la mayoría de los problemas del diagrama de Smith, las pérdidas se pueden suponer insignificantes ( ) y la tarea de resolverlas se simplifica enormemente. Por lo tanto, para el caso sin pérdidas, la expresión para el coeficiente de reflexión complejo se convierte en ${\displaystyle \gamma \,}$ ${\displaystyle \alpha \,}$ ${\displaystyle \alpha =0\,}$

${\displaystyle \Gamma =\Gamma _{\text{L}}\exp(-2j\beta \ell )\,}$

donde es el coeficiente de reflexión en la carga y es la longitud de la línea desde la carga hasta la ubicación donde se mide el coeficiente de reflexión. La constante de fase también se puede escribir como ${\displaystyle \Gamma _{\text{L}}\,}$ ${\displaystyle \ell \,}$ ${\displaystyle \beta \,}$

${\displaystyle \beta ={\frac {2\pi }{\lambda }}\,}$

donde es la longitud de onda dentro de la línea de transmisión en la frecuencia de prueba. ${\displaystyle \lambda \,}$

Por lo tanto,

${\displaystyle \Gamma =\Gamma _{\text{L}}\exp \left({\frac {-4j\pi }{\lambda }}\ell \right)\,}$

Esta ecuación muestra que, para una onda estacionaria, el coeficiente de reflexión complejo y la impedancia se repiten cada media longitud de onda a lo largo de la línea de transmisión. El coeficiente de reflexión complejo generalmente se denomina simplemente coeficiente de reflexión. La escala circunferencial exterior del diagrama de Smith representa la distancia desde el generador hasta la carga escalada en longitudes de onda y, por lo tanto, está escalada de cero a 0,50.

La variación de la impedancia normalizada con la posición a lo largo de la línea.

Si y son el voltaje a través de y la corriente que ingresa a la terminación al final de la línea de transmisión respectivamente, entonces ${\displaystyle \,V\,}$ ${\displaystyle \,I\,}$

${\displaystyle V_{\mathsf {F}}+V_{\mathsf {R}}=V\,}$

y

${\displaystyle V_{\mathsf {F}}-V_{\mathsf {R}}=Z_{0}\,I\,}$.

Dividiendo estas ecuaciones y sustituyendo ambas por el coeficiente de reflexión de voltaje

${\displaystyle \Gamma ={\frac {V_{\mathsf {R}}}{\,V_{\mathsf {F}}\,}}\,}$

y la impedancia normalizada de la terminación representada por la z minúscula , subíndice T

${\displaystyle z_{\mathsf {T}}={\frac {V}{\,Z_{0}\,I\,}}\,}$

da el resultado:

${\displaystyle z_{\mathsf {T}}={\frac {1+\Gamma }{\,1-\Gamma \,}}\,.}$

Alternativamente, en términos del coeficiente de reflexión

${\displaystyle \Gamma ={\frac {z_{\mathsf {T}}-1}{\,z_{\mathsf {T}}+1\,}}\,}$

Éstas son las ecuaciones que se utilizan para construir el diagrama Z de Smith. Matemáticamente hablando , están relacionadas a través de una transformación de Möbius . ${\displaystyle \,\Gamma \,}$ ${\displaystyle \,z_{\mathsf {T}}\,}$

Tanto y como se expresan en números complejos sin unidades. Ambos cambian con la frecuencia, por lo que para cualquier medición en particular, se debe indicar la frecuencia a la que se realizó junto con la impedancia característica. ${\displaystyle \,\Gamma \,}$ ${\displaystyle \,z_{\mathsf {T}}\,}$

${\displaystyle \,\Gamma \,}$puede expresarse en magnitud y ángulo en un diagrama polar . Cualquier coeficiente de reflexión real debe tener una magnitud menor o igual a la unidad , por lo que, en la frecuencia de prueba, esto puede expresarse mediante un punto dentro de un círculo de radio unitario. El diagrama de Smith está realmente construido sobre un diagrama polar de este tipo. La escala del diagrama de Smith está diseñada de tal manera que el coeficiente de reflexión se puede convertir en impedancia normalizada o viceversa. Usando el diagrama de Smith, la impedancia normalizada se puede obtener con una precisión apreciable trazando el punto que representa el coeficiente de reflexión tratando el diagrama de Smith como un diagrama polar y luego leyendo su valor directamente usando la escala característica del diagrama de Smith. Esta técnica es una alternativa gráfica a la sustitución de los valores en las ecuaciones.

Sustituyendo la expresión de cómo cambia el coeficiente de reflexión a lo largo de una línea de transmisión sin pérdidas sin igual

${\displaystyle \Gamma ={\frac {B\exp(-\gamma \ell )}{A\exp(\gamma \ell )}}={\frac {B\exp(-j\beta \ell )}{A\exp(j\beta \ell )}}\,}$

Para el caso sin pérdidas, en la ecuación de impedancia normalizada en términos de coeficiente de reflexión

${\displaystyle z_{\mathsf {T}}={\frac {1+\Gamma }{\,1-\Gamma \,}}\,.}$

y usando la fórmula de Euler

${\displaystyle \exp(j\theta )={\text{cis}}\,\theta =\cos \theta +j\,\sin \theta \,}$

produce la ecuación de línea de transmisión de versión de impedancia para el caso sin pérdidas: ^[24]

${\displaystyle Z_{\mathsf {in}}=Z_{0}{\frac {\,Z_{\mathsf {L}}+j\,Z_{0}\tan(\beta \ell )\,}{\,Z_{0}+j\,Z_{\mathsf {L}}\tan(\beta \ell )\,}}\,}$

¿Dónde se 've' la impedancia en la entrada de una línea de transmisión sin pérdidas de longitud terminada con una impedancia? ${\displaystyle \,Z_{\mathsf {in}}\,}$ ${\displaystyle \,\ell \,,}$ ${\displaystyle \,Z_{\mathsf {L}}\,}$

Se pueden derivar versiones de la ecuación de la línea de transmisión de manera similar para el caso sin pérdida de admitancia y para los casos con pérdida de impedancia y admitancia.

El equivalente gráfico del diagrama de Smith al uso de la ecuación de la línea de transmisión es normalizar para representar gráficamente el punto resultante en un diagrama de Smith Z y dibujar un círculo a través de ese punto centrado en el centro del diagrama de Smith. La trayectoria a lo largo del arco del círculo representa cómo cambia la impedancia a medida que se mueve a lo largo de la línea de transmisión. En este caso, se debe utilizar la escala circunferencial (longitud de onda), recordando que esta es la longitud de onda dentro de la línea de transmisión y puede diferir de la longitud de onda en el espacio libre. ${\displaystyle \,Z_{\mathsf {L}}\,,}$

Regiones de laODiagrama de Smith

Si se traza un diagrama polar sobre un sistema de coordenadas cartesianas, es convencional medir los ángulos relativos al eje x positivo utilizando una dirección contraria a las agujas del reloj para los ángulos positivos. La magnitud de un número complejo es la longitud de una línea recta trazada desde el origen hasta el punto que lo representa. El diagrama de Smith utiliza la misma convención, observando que, en el plano de impedancia normalizada, el eje x positivo se extiende desde el centro del diagrama de Smith en hasta el punto La región por encima del eje x representa impedancias inductivas (partes imaginarias positivas) y la región por debajo del eje x representa impedancias capacitivas (partes imaginarias negativas). ${\displaystyle \,z_{\mathsf {T}}=1\pm j0\,}$ ${\displaystyle \,z_{\mathsf {T}}=\infty \pm j\infty \,.}$

Si la terminación está perfectamente acoplada, el coeficiente de reflexión será cero, representado efectivamente por un círculo de radio cero o, de hecho, un punto en el centro de la tabla de Smith. Si la terminación fuera un circuito abierto o un cortocircuito perfecto , la magnitud del coeficiente de reflexión sería la unidad, se reflejaría toda la potencia y el punto se encontraría en algún punto de la circunferencia unitaria.

Círculos de resistencia normalizada constante y reactancia normalizada constante

El diagrama de Smith de impedancia normalizada se compone de dos familias de círculos: círculos de resistencia normalizada constante y círculos de reactancia normalizada constante. En el plano de coeficiente de reflexión complejo, el diagrama de Smith ocupa un círculo de radio unitario centrado en el origen. En coordenadas cartesianas, por lo tanto, el círculo pasaría por los puntos (+1,0) y (−1,0) en el eje x y los puntos (0,+1) y (0,−1) en el eje y .

Dado que tanto como son números complejos, en general pueden escribirse como: ${\displaystyle \,\Gamma \,}$ ${\displaystyle \,z_{\mathsf {T}}\,}$

${\displaystyle z_{\mathsf {T}}=a+jb\,}$

${\displaystyle ~\Gamma ~=c+jd\,}$

con números reales a , b , c y d .

Sustituyéndolos en la ecuación que relaciona la impedancia normalizada y el coeficiente de reflexión complejo:

${\displaystyle \Gamma ={\frac {z_{\mathsf {T}}-1}{\,z_{\mathsf {T}}+1\,}}={\frac {(a-1)+j\,b}{\,(a+1)+j\,b\,}}\,}$

da el siguiente resultado:

${\displaystyle \Gamma =c+jd=\left[{\frac {a^{2}+b^{2}-1}{\,(a+1)^{2}+b^{2}\,}}\right]+j\left[{\frac {2b}{\,(a+1)^{2}+b^{2}\,}}\right]=\left[1+{\frac {-2(a+1)}{\,(a+1)^{2}+b^{2}\,}}\right]+j\left[{\frac {+2b}{\,(a+1)^{2}+b^{2}\,}}\right]\,.}$

Esta es la ecuación que describe cómo el coeficiente de reflexión complejo cambia con la impedancia normalizada y puede usarse para construir ambas familias de círculos. ^[25]

ElYDiagrama de Smith

El diagrama de Smith Y se construye de manera similar al diagrama de Smith Z , pero expresando los valores del coeficiente de reflexión de voltaje en términos de admitancia normalizada en lugar de impedancia normalizada. La admitancia normalizada y _T es el recíproco de la impedancia normalizada z _T , por lo que

${\displaystyle y_{\mathsf {T}}={\frac {1}{z_{\mathsf {T}}}}\,}$

Por lo tanto:

${\displaystyle y_{\mathsf {T}}={\frac {1-\Gamma }{\,1+\Gamma \,}}\,}$

y

${\displaystyle \Gamma ={\frac {1-y_{\mathsf {T}}}{\,1+y_{\mathsf {T}}\,}}\,}$

El diagrama Y Smith aparece como el tipo de impedancia normalizado, pero con los círculos gráficos anidados rotados 180°, pero la escala numérica permanece en su misma posición (sin rotar) que el diagrama Z.

De manera similar, tomando

${\displaystyle y_{\mathsf {T}}={\tilde {o}}+j\,{\tilde {p}}\,}$

de verdad y da un resultado análogo, aunque con más y diferentes signos menos: ${\displaystyle \,{\tilde {o}}\,}$ ${\displaystyle \,{\tilde {p}}\,}$

${\displaystyle \Gamma =c+jd=\left[{\frac {1-{\tilde {o}}^{2}-{\tilde {p}}^{2}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]+j\left[{\frac {-2{\tilde {p}}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]=\left[{\frac {2({\tilde {o}}+1)}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}-1\right]+j\left[{\frac {-2{\tilde {p}}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]\,.}$

La región por encima del eje x representa admitancias capacitivas y la región por debajo del eje x representa admitancias inductivas. Las admitancias capacitivas tienen partes imaginarias positivas y las admitancias inductivas tienen partes imaginarias negativas.

Nuevamente, si la terminación coincide perfectamente, el coeficiente de reflexión será cero, representado por un "círculo" de radio cero o, de hecho, un punto en el centro del diagrama de Smith. Si la terminación fuera un circuito abierto o un cortocircuito perfecto, la magnitud del coeficiente de reflexión de voltaje sería la unidad, toda la potencia se reflejaría y el punto se ubicaría en algún punto del círculo circunferencial unitario del diagrama de Smith.

Ejemplos prácticos

Puntos de ejemplo graficados en el diagrama de Smith de impedancia normalizada.

Un punto con un coeficiente de reflexión de magnitud 0,63 y un ángulo de 60° representado en forma polar como , se muestra como el punto P ₁ en la carta de Smith. Para trazarlo, se puede utilizar la escala de ángulos circunferenciales (coeficiente de reflexión) para encontrar la graduación y una regla para dibujar una línea que pase por este y el centro de la carta de Smith. La longitud de la línea se escalaría entonces a P ₁ suponiendo que el radio de la carta de Smith es la unidad. Por ejemplo, si el radio real medido a partir del papel fue de 100 mm, la longitud OP ₁ sería de 63 mm. ${\displaystyle 0.63\angle 60^{\circ }\,}$ ${\displaystyle \angle 60^{\circ }\,}$

La siguiente tabla muestra algunos ejemplos similares de puntos representados en el diagrama de Smith Z. Para cada uno de ellos, el coeficiente de reflexión se proporciona en forma polar junto con la impedancia normalizada correspondiente en forma rectangular. La conversión se puede leer directamente en el diagrama de Smith o mediante sustitución en la ecuación.

Trabajando con ambosODiagrama de Smith y elYDiagramas de Smith

En los problemas de adaptación y circuitos de RF, a veces es más conveniente trabajar con admitancias (que representan conductancias y susceptancias ) y, a veces, es más conveniente trabajar con impedancias (que representan resistencias y reactancias ). La solución de un problema de adaptación típico a menudo requerirá varios cambios entre ambos tipos de diagrama de Smith, utilizando impedancia normalizada para elementos en serie y admitancias normalizadas para elementos en paralelo . Para estos, se puede utilizar un diagrama de Smith de impedancia y admitancia dual (normalizada). Alternativamente, se puede utilizar un tipo y convertir la escala al otro cuando sea necesario. Para cambiar de impedancia normalizada a admitancia normalizada o viceversa, el punto que representa el valor del coeficiente de reflexión en consideración se mueve exactamente 180 grados en el mismo radio. Por ejemplo, el punto P1 en el ejemplo que representa un coeficiente de reflexión de tiene una impedancia normalizada de . Para cambiar gráficamente esto al punto de admitancia normalizado equivalente, digamos Q1, se dibuja una línea con una regla desde P1 a través del centro del diagrama de Smith hasta Q1, un radio igual en la dirección opuesta. Esto es equivalente a mover el punto a través de una trayectoria circular de exactamente 180 grados. Al leer el valor del diagrama de Smith para Q1, recordando que la escala ahora está en admitancia normalizada, se obtiene . Realizar el cálculo ${\displaystyle 0.63\angle 60^{\circ }\,}$ ${\displaystyle z_{P}=0.80+j1.40\,}$ ${\displaystyle y_{P}=0.30-j0.54\,}$

${\displaystyle y_{\text{T}}={\frac {1}{z_{\text{T}}}}\,}$

confirmará esto manualmente.

Una vez que se ha realizado una transformación de impedancia a admitancia, la escala cambia a admitancia normalizada hasta que se realiza una transformación posterior nuevamente a impedancia normalizada.

La siguiente tabla muestra ejemplos de impedancias normalizadas y sus admitancias normalizadas equivalentes obtenidas mediante la rotación del punto 180°. Nuevamente, estas pueden obtenerse ya sea por cálculo o utilizando una tabla de Smith como se muestra, convirtiendo entre los planos de impedancia normalizada y admitancia normalizada.

Valores del coeficiente de reflexión complejo graficados en la carta de Smith de impedancia normalizada y sus equivalentes en la carta de Smith de admitancia normalizada.

Selección del tipo de diagrama de Smith y del tipo de componente

La elección de si se debe utilizar la tabla de Smith Z o la tabla de Smith Y para cualquier cálculo particular depende de cuál sea más conveniente. Las impedancias en serie y las admitancias en paralelo se suman, mientras que las impedancias en paralelo y las admitancias en serie están relacionadas por una ecuación recíproca. Si es la impedancia equivalente de las impedancias en serie y es la impedancia equivalente de las impedancias en paralelo, entonces ${\displaystyle Z_{\text{TS}}}$ ${\displaystyle Z_{\text{TP}}}$

${\displaystyle Z_{\text{TS}}=Z_{1}+Z_{2}+Z_{3}+...\,}$

${\displaystyle {\frac {1}{Z_{\text{TP}}}}={\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}+{\frac {1}{Z_{3}}}+...\,}$

En el caso de las admisiones, ocurre lo contrario, es decir:

${\displaystyle Y_{\text{TP}}=Y_{1}+Y_{2}+Y_{3}+...\,}$

${\displaystyle {\frac {1}{Y_{\text{TS}}}}={\frac {1}{Y_{1}}}+{\frac {1}{Y_{2}}}+{\frac {1}{Y_{3}}}+...\,}$

El manejo de los recíprocos , especialmente en números complejos, requiere más tiempo y es más propenso a errores que el uso de la suma lineal. Por lo tanto, en general, la mayoría de los ingenieros de RF trabajan en el plano donde la topografía del circuito admite la suma lineal. La siguiente tabla muestra las expresiones complejas para la impedancia (real y normalizada) y la admitancia (real y normalizada) para cada uno de los tres elementos básicos del circuito pasivo : resistencia, inductancia y capacitancia. Utilizando solo la impedancia característica (o admitancia característica) y la frecuencia de prueba, se puede encontrar un circuito equivalente y viceversa.

Uso del diagrama de Smith para resolver problemas de correspondencia conjugada con componentes distribuidos

La adaptación distribuida se hace posible y a veces es necesaria cuando el tamaño físico de los componentes de adaptación es mayor que aproximadamente el 5% de una longitud de onda en la frecuencia de operación. En este caso, el comportamiento eléctrico de muchos componentes agrupados se vuelve bastante impredecible. Esto ocurre en circuitos de microondas y cuando la alta potencia requiere componentes grandes en transmisiones de onda corta, FM y TV.

Para los componentes distribuidos, se deben tener en cuenta los efectos sobre el coeficiente de reflexión y la impedancia del movimiento a lo largo de la línea de transmisión para utilizar la escala circunferencial exterior de la carta de Smith, que está calibrada en longitudes de onda.

El siguiente ejemplo muestra cómo una línea de transmisión, terminada con una carga arbitraria, puede conectarse en una frecuencia con un componente reactivo en serie o en paralelo, en cada caso conectado en posiciones precisas.

Construcción de un diagrama de Smith para la correspondencia de algunas líneas de transmisión distribuidas.

Supongamos que una línea de transmisión sin pérdidas con espaciado por aire y de impedancia característica , que opera a una frecuencia de 800 MHz, termina con un circuito que comprende una resistencia de 17,5 en serie con un inductor de 6,5 nanohenrios (6,5 nH). ¿Cómo se puede adaptar la línea? ${\displaystyle Z_{0}=50\ \Omega }$ ${\displaystyle \Omega }$

De la tabla anterior, la reactancia del inductor que forma parte de la terminación a 800 MHz es

${\displaystyle Z_{L}=j\omega L=j2\pi fL=j32.7\ \Omega \,}$

Por lo tanto, la impedancia de la combinación ( ) viene dada por ${\displaystyle Z_{T}}$

${\displaystyle Z_{T}=17.5+j32.7\ \Omega \,}$

y la impedancia normalizada ( ) es ${\displaystyle z_{T}}$

${\displaystyle z_{T}={\frac {Z_{T}}{Z_{0}}}=0.35+j0.65\,}$

Esto se representa en el diagrama de Smith Z en el punto P _20. La línea OP ₂₀ se extiende hasta la escala de longitud de onda donde se cruza en el punto . Como la línea de transmisión no tiene pérdidas, se dibuja un círculo centrado en el centro del diagrama de Smith a través del punto P ₂₀ para representar la trayectoria del coeficiente de reflexión de magnitud constante debido a la terminación. En el punto P _21, el círculo se cruza con el círculo unitario de resistencia normalizada constante en ${\displaystyle L_{1}=0.098\lambda \,}$

${\displaystyle z_{P21}=1.00+j1.52\,}$.

La prolongación de la línea OP ₂₁ intersecta la escala de longitud de onda en , por lo tanto, la distancia desde la terminación hasta este punto de la línea está dada por ${\displaystyle L_{2}=0.177\lambda \,}$

${\displaystyle L_{2}-L_{1}=0.177\lambda -0.098\lambda =0.079\lambda \,}$

Dado que la línea de transmisión está espaciada en el aire, la longitud de onda a 800 MHz en la línea es la misma que en el espacio libre y está dada por

${\displaystyle \lambda ={\frac {c}{f}}\,}$

donde es la velocidad de la radiación electromagnética en el espacio libre y es la frecuencia en hercios. El resultado es , lo que hace que la posición del componente correspondiente esté a 29,6 mm de la carga. ${\displaystyle c\,}$ ${\displaystyle f\,}$ ${\displaystyle \lambda =375\ \mathrm {mm} \,}$

La coincidencia conjugada para la impedancia en P ₂₁ ( ) es ${\displaystyle z_{match}\,}$

${\displaystyle z_{match}=-j(1.52),\!}$

Como el diagrama de Smith todavía está en el plano de impedancia normalizado, de la tabla anterior se requiere un capacitor en serie donde ${\displaystyle C_{m}\,}$

${\displaystyle z_{match}=-j1.52={\frac {-j}{\omega C_{m}Z_{0}}}={\frac {-j}{2\pi fC_{m}Z_{0}}}\,}$

Reordenando, obtenemos

${\displaystyle C_{m}={\frac {1}{(1.52)\omega Z_{0}}}={\frac {1}{(1.52)(2\pi f)Z_{0}}}}$.

La sustitución de valores conocidos da

${\displaystyle C_{m}=2.6\ \mathrm {pF} \,}$

Para hacer coincidir la terminación a 800 MHz, se debe colocar un condensador en serie de 2,6 pF en serie con la línea de transmisión a una distancia de 29,6 mm de la terminación.

Se podría calcular una adaptación de derivación alternativa después de realizar una transformación de diagrama de Smith de impedancia normalizada a admitancia normalizada. El punto Q ₂₀ es el equivalente de P ₂₀ pero expresado como una admitancia normalizada. Al leer la escala del diagrama de Smith, recordando que ahora se trata de una admitancia normalizada, se obtiene

${\displaystyle y_{Q20}=0.65-j1.20\,}$

(De hecho, este valor no se utiliza realmente). Sin embargo, la extensión de la línea OQ ₂₀ a través de la escala de longitud de onda da . El punto más temprano en el que se podría introducir una adaptación conjugada en derivación, moviéndose hacia el generador, sería en Q _{21 , la misma posición que el P 21} anterior , pero esta vez representando una admitancia normalizada dada por ${\displaystyle L_{3}=0.152\lambda \,}$

${\displaystyle y_{Q21}=1.00+j1.52\,}$.

La distancia a lo largo de la línea de transmisión es en este caso

${\displaystyle L_{2}+L_{3}=0.177\lambda +0.152\lambda =0.329\lambda \,}$

que convierte a 123 mm.

Se requiere que el componente de coincidencia conjugada tenga una admitancia normalizada ( ) de ${\displaystyle y_{match}}$

${\displaystyle y_{match}=-j1.52\,}$.

De la tabla se desprende que una admitancia negativa requeriría un inductor conectado en paralelo con la línea de transmisión. Si su valor es , entonces ${\displaystyle L_{m}\,}$

${\displaystyle -j1.52={\frac {-j}{\omega L_{m}Y_{0}}}={\frac {-jZ_{0}}{2\pi fL_{m}}}\,}$

Esto da el resultado

${\displaystyle L_{m}=6.5\ \mathrm {nH} \,}$

Por lo tanto, una adaptación de derivación inductiva adecuada sería un inductor de 6,5 nH en paralelo con la línea colocada a 123 mm de la carga.

Uso del diagrama de Smith para analizar circuitos de elementos concentrados

El análisis de componentes de elementos concentrados supone que la longitud de onda a la frecuencia de operación es mucho mayor que las dimensiones de los propios componentes. Se puede utilizar la carta de Smith para analizar dichos circuitos, en cuyo caso los movimientos alrededor de la carta son generados por las impedancias y admitancias (normalizadas) de los componentes a la frecuencia de operación. En este caso, no se utiliza la escala de longitud de onda en la circunferencia de la carta de Smith. El siguiente circuito se analizará utilizando una carta de Smith a una frecuencia de operación de 100 MHz. A esta frecuencia, la longitud de onda en el espacio libre es de 3 m. Las dimensiones de los componentes serán del orden de milímetros, por lo que la suposición de componentes concentrados será válida. A pesar de que no hay una línea de transmisión como tal, se debe definir una impedancia del sistema para permitir los cálculos de normalización y desnormalización y es una buena opción en este caso, ya que . Si hubiera valores de resistencia muy diferentes, un valor más cercano a estos podría ser una mejor opción. ${\displaystyle Z_{0}=50\ \Omega \,}$ ${\displaystyle R_{1}=50\ \Omega \,}$

Un circuito de elementos concentrados que puede analizarse utilizando un diagrama de Smith.

Diagrama de Smith con construcción gráfica para el análisis de un circuito concentrado.

El análisis comienza con un diagrama de Smith Z que analiza únicamente R ₁ sin otros componentes presentes. Al igual que la impedancia del sistema, esto se representa mediante un punto en el centro del diagrama de Smith. La primera transformación es OP ₁ a lo largo de la línea de resistencia normalizada constante; en este caso, se agrega una reactancia normalizada de - j 0,80, que corresponde a un capacitor en serie de 40 pF. Los puntos con sufijo P están en el plano Z y los puntos con sufijo Q están en el plano Y. Por lo tanto, las transformaciones P ₁ a Q ₁ y P ₃ a Q ₃ son del diagrama de Smith Z al diagrama de Smith Y, y la transformación Q ₂ a P ₂ es del diagrama de Smith Y al diagrama de Smith Z. La siguiente tabla muestra los pasos que se tomaron para trabajar con los componentes y transformaciones restantes, regresando finalmente al centro del diagrama de Smith y una coincidencia perfecta de 50 ohmios. ${\displaystyle R_{1}=50\ \Omega \,}$

Diagrama de Smith en 3D

Representación del diagrama de Smith en 3D.

Muller et al. propusieron en 2011 una generalización del diagrama de Smith a una esfera tridimensional, basada en el plano complejo extendido ( esfera de Riemann ) y la geometría inversa . ^[26]

El diagrama unifica el diseño de circuitos pasivos y activos en círculos pequeños y grandes sobre la superficie de una esfera unitaria, utilizando un mapa conforme estereográfico del plano generalizado del coeficiente de reflexión. Considerando el punto en el infinito, el espacio del nuevo diagrama incluye todas las cargas posibles: el polo norte es el punto perfectamente emparejado, mientras que el polo sur es el punto completamente desapareado. ^[26]

El diagrama de Smith 3D se ha ampliado más allá de la superficie esférica para representar gráficamente diversos parámetros escalares, como el retardo de grupo, los factores de calidad o la orientación de frecuencia. La orientación visual de la frecuencia (en sentido horario o antihorario) permite diferenciar entre un negativo/capacitancia y un positivo/inductivo cuyos coeficientes de reflexión son los mismos cuando se representan gráficamente en un diagrama de Smith 2D, pero cuyas orientaciones divergen a medida que aumenta la frecuencia. ^[27]

Véase también

• Mosaico binario
• Diagrama de Bode
• El complot de Nyquist
• Diagrama circular de Heyland-Ossanna
• cis (matemáticas)
• Transversal (construcción de instrumentos)

Referencias

1. Okamura [岡村], Fumiyoshi [史良] / Shirō [獅郎] (agosto de 1959) [4 de abril de 1959]. "Sumisuchāto wa nihonjin no dokusōde wanai ka" スミスチャートは日本人の独創ではないか ["Smith Chart" puede tener origen en Japón] (PDF) . Revista del Instituto de Ingenieros de Comunicaciones Eléctricas de Japón [電気通信学会雑誌] (en japonés). 1959 (8). Tokio, Japón: Instituto de Ingenieros de Comunicaciones Eléctricas de Japón [電気通信学会]: 768–769 (44–45). ISSN  0914-5273. Archivado desde el original (PDF) el 16 de noviembre de 2017.(2 páginas) (NB: El artículo indica el nombre de pila del autor como史良en japonés, que se traduciría como "Fumiyoshi", mientras que la nota al pie en inglés del mismo artículo lo transcribió como "Shirō", que se asociaría con獅郎en japonés).
2. Kenichi [伊藤健], Ito [一著] (1 de noviembre de 1999). Inpidansu no hanashi インピーダンスのはなし[ La historia de la impedancia ]. Ciencia y Tecnología (en japonés) (1 ed.). Nikkan Kogyo Shimbun [日刊工業新聞社]. pag. 26.ISBN​ 4-526-04463-6. EAN  978-4-526-04463-2. 1923054018007.(4+xi+1+207+3+4 páginas)
3. Mori [森], Kunihiko [邦彦] (2013). "El gráfico de Mizuhashi-Smith". morikuni_net . Archivado desde el original el 3 de marzo de 2013 . Consultado el 24 de junio de 2023 .
4. Kurochkin [Курочкин], Alexander Evdokimovich [Александр Евдокимович] (2009). "Diagramma Vol'perta – Smita. Raschet i analiz kharakteristik usiliteley radiosignalov" Диаграмма Вольперта – Смита. Análisis y análisis de características de radiocomunicaciones [El diagrama de Volpert-Smith. Cálculo y análisis de las características de amplificadores de señales de radio] (PDF) (en ruso). Minsk, Bielorrusia: Departamento de Dispositivos de Ingeniería de Radio, Universidad Estatal de Informática y Radioelectrónica de Bielorrusia, institución educativa del Ministerio de Educación de la República de Bielorrusia. ISBN 978-9-85-488-422-6. Archivado (PDF) desde el original el 9 de julio de 2023 . Consultado el 9 de julio de 2023 . pag. 4: Diagrama Smita ostayetsya odnim iz naiboleye poleznykh graficheskikh instrumentov dlya razrabotki vysokochastotnykh usilitel'nykh kaskadov. V nashey strane analogichnaya diagrama izvestna kak krugovaya nomogramma AR Vol'perta, kotoryy v 1939 g. nezavisimo ot Smita razrabotal i primenil yeye dlya pereschota provodimostey i soprotivleniy v otrezkakh liniy peredachi. El diagrama muestra cómo se muestran los instrumentos gráficos de los usuarios каскадов. В нашей стране аналогичная диаграмма известна как круговая номограмма А. Р. Вольперта, который en 1939 г. Nezavisimo от Смита разработал и применил ее для пересчёта проводимостей и сопротивлений в отрезках линий передачи.[En nuestro país un diagrama similar se conoce como nomograma circular de AR Volpert, quien en 1939, independientemente de Smith, lo desarrolló y aplicó para recalcular conductancias y resistencias en segmentos de líneas de transmisión.][1][2][3] (40+1 páginas)
5. Salov, Mikhail (marzo de 2022). "4. Diagrama de Volpert–Smith". Medición y adaptación de impedancia de antena (PDF) (nota de aplicación). Texas Instruments . pág. 11. SWRA726. Archivado (PDF) desde el original el 2023-06-26 . Consultado el 2023-06-26 .(51 páginas)
6. Ramo, Simon "Si" ; Whinnery, John Roy ; Van Duzer, Theodore (1965). Campos y ondas en la electrónica de comunicaciones (1.ª ed.). John Wiley & Sons . págs. 35–39.
7. Ramo, Simon "Si" ; Whinnery, John Roy ; Van Duzer, Theodore (1994). "5.9. El diagrama de líneas de transmisión de Smith / 5.10. Algunos usos del diagrama de Smith". Campos y ondas en la electrónica de comunicaciones (3.ª ed.). John Wiley & Sons, Inc. págs. 236–245. ISBN 978-0-471-58551-0.
8. Smith, Phillip Hagar (junio de 1969). Escrito en Pine Brook, Nueva Jersey, EE. UU. Aplicaciones electrónicas del diagrama de Smith: en Análisis de componentes, circuitos y guías de ondas (1.ª ed.). Nueva York, EE. UU.: McGraw-Hill Book Company / Kay Electric Company. ISBN 0-07058930-5. LCCN  69-12411. ISBN 978-0-07058930-8 . (xxvii+1+222 páginas + sobre con 4 capas de plástico translúcido + postal de Kay Electric Company) (NB: Hay una reimpresión de 1983 de la primera edición de Robert E. Krieger Publishing Company con ISBN 978-0-89874-552-8 , 0-89874-552-7 y una segunda edición de Noble Publishing Corporation). 
9. Smith, Phillip Hagar (octubre de 2000) [1995]. Aplicaciones electrónicas del diagrama de Smith: en Análisis de circuitos, componentes y guías de onda (2.ª ed.). Atlanta, Georgia, EE. UU.: Noble Publishing Corporation . ISBN 1-884932-39-8. LCCN  00-045239. ISBN 978-1-884932-39-7 . p. xiv: […] A partir de la ecuación de Fleming , ^[A] y en un esfuerzo por simplificar la solución del problema de la línea de transmisión, desarrolló su primera solución gráfica en forma de un diagrama rectangular. […] el diagrama evolucionó gradualmente a través de una serie de pasos. El primer diagrama rectangular estaba limitado por el rango de datos que podía acomodar. Era consciente de las limitaciones y siguió trabajando en el problema hasta algún momento en 1936, cuando desarrolló un nuevo diagrama que eliminó la mayoría de las dificultades. El nuevo diagrama era una forma especial de coordenadas polares en la que se podían acomodar todos los valores de los componentes de impedancia. Los datos para este diagrama se escalaron a partir del diagrama rectangular anterior. Las coordenadas de impedancia en este caso no eran ortogonales y no eran círculos verdaderos, pero, en la forma elegida, la relación de ondas estacionarias era lineal. El diagrama se parecía mucho a lo que finalmente se convirtió en el resultado final. Phil , sin embargo, sospechaba que una cuadrícula formada por un sistema de círculos ortogonales podría ser más práctica. Pensó que tendría claras ventajas, particularmente en lo que respecta a la reproducibilidad. Con esto en mente, habló con dos de sus compañeros de trabajo, EB Ferrell y JW McRae . Como estaban familiarizados con los principios del mapeo conforme , pudieron desarrollar la transformación mediante la cual se podían acomodar todos los datos desde cero hasta el infinito. Afortunadamente, las curvas de relación de onda estacionaria constante, atenuación constante y coeficiente de reflexión constante eran todos círculos coaxiales con el centro del diagrama. Las escalas para estos valores, aunque no lineales, eran completamente satisfactorias. Un diagrama diseñado de acuerdo con estas líneas se construyó a principios de 1937. Era esencialmente la forma que todavía se usa hoy. Smith se acercó a varias revistas técnicas con respecto a la publicación del diagrama, pero la aceptación fue lenta. No había muchas revistas técnicas en ese momento, y ninguna en el área de microondas. Sin embargo, en enero de 1939, después de un retraso de dos años, el artículo fue impreso en la revista Electronics . […] (xxvi+237+1 páginas + sobre con 4 capas de plástico translúcido) (NB: Hay una reimpresión de 2006 de la segunda edición realizada por SciTech Publishing, Inc. con el mismo ISBN y LCCN).
10. "Igualación de impedancia e impedancia de la tabla Smith" (nota de aplicación). Maxim Integrated Products, Inc. 2012 [2002-07-22]. Tutorial 742. Archivado desde el original el 2023-07-09 . Consultado el 2023-07-09 .[4] (18 páginas) (NB. Una versión anterior de este artículo apareció en la edición de julio de 2000 de RF Design ).
11. Voltmer, David (17 de agosto de 2007). "8.2. El diagrama de Smith". En Balanis, Constantine A. (ed.). Fundamentos de electromagnetismo 2. Cuasistáticos y ondas. Lecciones de síntesis sobre electromagnetismo computacional. Vol. 2 (1.ª ed.). Morgan y Claypool . págs. 135–141 [135]. doi :10.2200/S00078ED1V01Y200612CEM015. ISBN . 978-1-59829172-8. ISSN  1932-1716. S2CID  9045052. ISBN 1-59829172-6 . LoC 1932-1252. MOBK081-FM . Consultado el 25 de junio de 2023 . p. 135: Aunque Volpert de la Unión Soviética y Mizuhashi de Japón propusieron esencialmente el mismo gráfico durante el mismo año, Smith recibió el reconocimiento. 
12. "Gráfico de Smith". ETHW.org . 2018-02-26. Archivado desde el original el 2023-07-08 . Consultado el 2021-03-30 .
13. Mizuhashi [水橋], Tōsaku [東作] (diciembre de 1937) [19 de noviembre de 1937]. "Sì duānzǐ huílù no inpīdansu hensei to seigō kairo no riron" 四端子回路のインピーダンス変成と整合回路の理論 [Teoría del circuito de transformación de impedancia de cuatro terminales y del circuito de adaptación ] (PDF) . Revista del Instituto de Ingenieros de Comunicaciones Eléctricas de Japón [電気通信学会雑誌] (en japonés). 1937 (12). Instituto de Ingenieros de Comunicaciones Eléctricas de Japón [電気通信学会]: 1053–1058 (29–34). ISSN  0914-5273. Archivado desde el original (PDF) el 16 de noviembre de 2017.(6 páginas)
14. Volpert [Во́льперт], Amiel Rafailovich [Амиэ́ль Рафаи́лович] [en ruso] (febrero de 1940). "Nomograma dlya rascheta dlinnykh liniy"Номограмма для расчета длинных линий[Nomograma para calcular líneas largas]. Производственно-технический бюллетень (Proizvodstvenno-tekhnicheskiy byulleten') [Boletín técnico e industrial] (en ruso). vol. 1940, núm. 2. Leningrado , СССР: НКЭП  [ru] . págs. 14-18.(5 páginas)
15. Smith, Phillip Hagar (enero de 1939). «Calculadora de líneas de transmisión: una calculadora de «corte» para determinar la impedancia y la atenuación, en términos de la longitud de líneas de transmisión de cable abierto» (PDF) . Electrónica : radio, comunicación, aplicaciones industriales de tubos electrónicos... ingeniería y fabricación . Vol. 12, núm. 1. Nueva York, EE. UU.: McGraw-Hill Publishing Company, Inc. págs. 29–31. ISSN  0013-5070. Archivado (PDF) desde el original el 8 de julio de 2023. Consultado el 9 de julio de 2023 .(3 páginas)
16. Smith, Phillip Hagar (enero de 1944). «An Improved Transmission Line Calculator - An extension of the "calculator" createdly published in ELECTRONICS in January 1939. New parameters have been added and precision has been improved» (PDF) . electrónica . Vol. 17, no. 1. Nueva York, EE. UU.: McGraw-Hill Publishing Company, Inc. pp. 130–133, 318, 320, 322, 324–325. ISSN  0013-5070. Archivado (PDF) desde el original el 2023-01-31 . Consultado el 2023-07-09 .(4+5 páginas)
17. Inan, Aziz S. (3 de julio de 2005). Escrito en la Escuela de Ingeniería de la Universidad de Portland, Portland, Oregón, EE. UU. Recordando a Phillip H. Smith en su centenario (PDF) . 2005 IEEE Antennas and Propagation Society International Symposium Digest . Vol. 3B. Washington, DC, EE. UU.: IEEE Antennas and Propagation Society . págs. 129–132. doi :10.1109/APS.2005.1552450. eISSN  1947-1491. ISBN 0-7803-8883-6. ISSN  1522-3965. Archivado (PDF) desde el original el 2023-07-02 . Consultado el 2023-07-02 .(NB. Esta es una versión corregida del artículo publicado originalmente).
18. Linton, Jr., RL (enero de 1950). Escrito en Antenna Laboratory, University of California, Berkeley, California, EE. UU. "Gráfico para diagrama de Smith" (PDF) . electrónica . Vol. 23, núm. 1. Nueva York, EE. UU.: McGraw-Hill Publishing Company, Inc. pp. 123, 158. ISSN  0013-5070. Archivado (PDF) desde el original el 31 de enero de 2023. Consultado el 22 de julio de 2023 .
19. "Impedance Measurement-Smith Chart with Example Plotted" (PDF) . General Radio Experimenter . Vol. XXV, no. 6. Cambridge, Massachusetts, EE. UU.: General Radio Company . Noviembre de 1950. págs. 5-7. Archivado (PDF) desde el original el 22 de julio de 2023 . Consultado el 22 de julio de 2023 .
20. Pozar, David Michael (2005). Ingeniería de microondas (3.ª edición). John Wiley & Sons, Inc., págs. 64-71. ISBN 0-471-44878-8.
21. Gonzalez, Guillermo (1997). Microwave Transistor Amplifiers Analysis and Design (2da. ed.). Nueva Jersey, EE. UU.: Prentice Hall . pp. 93–103. ISBN 0-13-254335-4.
22. Bevelacqua, Peter Joseph (11 de enero de 2013) [2010]. "El diagrama de Smith". www.antenna-theory.com . Archivado desde el original el 8 de julio de 2023 . Consultado el 9 de julio de 2023 .
23. "Adaptación de antena con un analizador de redes vectoriales". Tek . Tektronix, Inc. 2017-10-06. Archivado desde el original el 2023-07-08 . Consultado el 2023-07-09 .
24. Hayt, Jr., William Hart [en Wikidata] (1981). Ingeniería Electromagnética (4 ed.). McGraw-Hill, Inc. págs. 428–433. ISBN 0-07-027395-2.(527 páginas)
25. Davidson, Colin William (1989). Líneas de transmisión para comunicaciones con programas CAD (2.ª edición). Basingstoke, Hampshire, Reino Unido: Macmillan Education Ltd. pp. 80–85. ISBN 0-333-47398-1. ark:/13960/s2dzmfrhg24 . Consultado el 9 de julio de 2023 .(viii+244 páginas)
26. Muller, Andrei A.; Soto Pacheco, Pablo; Dascălu, Dan [en rumano] ; Neculoiu, Dan; Boria, Vicente E. (2011). "Un diagrama de Smith 3D basado en la esfera de Riemann para circuitos de microondas activos y pasivos". IEEE Microwave and Wireless Components Letters . 21 (6). IEEE Microwave Theory and Techniques Society : 286–288. doi :10.1109/LMWC.2011.2132697. hdl : 10251/55107 . ISSN  1531-1309. S2CID  38953650.
27. Muller, Andrei A.; Asavei, Victor; Moldoveanu, Alin; Sanabria-Codesal, Esther; Khadar, Riyaz A.; Popescu, Cornel; Dascălu, Dan [en rumano] ; Ionescu, Adrian M. (noviembre de 2020). "El diagrama de Smith 3D: de la teoría a la realidad experimental". Revista IEEE Microwave . 21 (11). Sociedad de teoría y técnicas de microondas IEEE : 22–35. doi :10.1109/MMM.2020.3014984. ISSN  1527-3342. S2CID  222296721.

Lectura adicional

• Campbell, George Ashley (abril de 1911). "Oscilaciones cisoidales" (PDF) . Actas del Instituto Americano de Ingenieros Eléctricos . XXX (1–6). Instituto Americano de Ingenieros Eléctricos : 789–824 [Fig. 13 en la pág. 810]. doi :10.1109/PAIEE.1911.6659711. S2CID  51647814 . Consultado el 24 de junio de 2023 .(37 páginas) (NB. Incluye una representación gráfica temprana de algo similar a un diagrama de Smith décadas antes de que Mizuhashi, Volpert y Smith publicaran sus trabajos).
• Fleming, John Ambrose (enero de 1912) [mayo de 1911]. Propagación de corrientes eléctricas en conductores telefónicos y telegráficos: un curso de conferencias de posgrado dictadas ante la Universidad de Londres (segunda edición revisada). University College, Londres, Reino Unido: Constable & Company Ltd. ark:/13960/t3bz6211d . Consultado el 23 de julio de 2023 .(xiv+316 páginas)
• Krauss, Herbert L. (septiembre de 1949). "Transmission Line Charts". Ingeniería eléctrica . Vol. 68, núm. 9. págs. 766–774 [767]. doi :10.1109/EE.1949.6444963. eISSN  2376-7804. ISSN  0095-9197.
• Lee, Donald (30 de enero de 2013). "Ajuste del diagrama de Smith, parte I". Unidad de negocio SOC, Advantest Test Cell Innovations, Advantest Corporation . Archivado desde el original el 9 de julio de 2023. Consultado el 9 de julio de 2023 .(29 páginas)
• Gamblin, Trevor (23 de julio de 2015). "Construcción matemática y propiedades del diagrama de Smith". allaboutcircuits.com . Archivado desde el original el 9 de julio de 2023 . Consultado el 9 de julio de 2023 .
• Staples, John (2015). "Igualación de impedancia y diagramas de Smith" (PDF) . Escuela de Aceleradores de Partículas de Estados Unidos (USPAS). Archivado (PDF) desde el original el 2023-07-09 . Consultado el 2023-07-09 .(27 páginas)

Enlaces externos

• "Gráfico de Smith de Excel". excelhero.com . Agosto de 2010.Diagrama de Smith interactivo y no comercial que se ve mejor en Excel 2007+.
• "SimSmith". ae6ty.com .No comercial, disponible para Windows, Mac y Linux. Muchos videos tutoriales sobre diagramas de Smith. Sin restricciones de tamaño de circuito. No se limita a circuitos en escalera.
• "Smith v3". fritz.dellsperger.net . Archivado desde el original el 4 de marzo de 2015.Diagrama de Smith comercial y gratuito para Windows
• "QuickSmith". github.com/niyeradori . 2 de noviembre de 2021.Herramienta educativa gratuita basada en web Smith Chart disponible en GitHub .
• "Herramienta de diagrama de Smith 3D". 3dsmithchart.com .Herramienta generalizada de diagramas de Smith 2D y 3D para circuitos activos y pasivos (gratuita para el ámbito académico/educativo).