Inducción matemática

Forma de prueba matemática

La inducción matemática se puede ilustrar informalmente con referencia al efecto secuencial de la caída de fichas de dominó . ^{[1] [2]}

La inducción matemática es un método para demostrar que una afirmación es verdadera para cada número natural , es decir, que todos los casos   son válidos. Esto se hace demostrando primero un caso simple y luego demostrando que si suponemos que la afirmación es verdadera para un caso dado, entonces el siguiente caso también es verdadero. Las metáforas informales ayudan a explicar esta técnica, como la caída de fichas de dominó o subir una escalera: ${\displaystyle P(n)}$ ${\displaystyle n}$ ${\displaystyle P(0),P(1),P(2),P(3),\dots }$

La inducción matemática demuestra que podemos subir tan alto como queramos en una escalera, al demostrar que podemos subir hasta el peldaño inferior (la base ) y que desde cada peldaño podemos subir al siguiente (el escalón ).

—  Matemáticas Concretas , página 3 márgenes.

Una demostración por inducción consta de dos casos. El primero, el caso base , prueba la afirmación para sin suponer ningún conocimiento de otros casos. El segundo caso, el paso de inducción , prueba que si la afirmación es válida para cualquier caso dado , entonces también debe ser válida para el siguiente caso . Estos dos pasos establecen que la afirmación es válida para todo número natural . El caso base no necesariamente comienza con , pero a menudo con , y posiblemente con cualquier número natural fijo , lo que establece la verdad de la afirmación para todos los números naturales . ${\displaystyle n=0}$ ${\displaystyle n=k}$ ${\displaystyle n=k+1}$ ${\displaystyle n}$ ${\displaystyle n=0}$ ${\displaystyle n=1}$ ${\displaystyle n=N}$ ${\displaystyle n\geq N}$

El método puede extenderse para probar afirmaciones sobre estructuras bien fundadas más generales , como los árboles ; esta generalización, conocida como inducción estructural , se utiliza en lógica matemática y en informática . La inducción matemática en este sentido extendido está estrechamente relacionada con la recursión . La inducción matemática es una regla de inferencia utilizada en pruebas formales y es la base de la mayoría de las pruebas de corrección de los programas informáticos. ^[3]

A pesar de su nombre, la inducción matemática difiere fundamentalmente del razonamiento inductivo tal como se utiliza en filosofía , en el que el examen de muchos casos da como resultado una conclusión probable. El método matemático examina una cantidad infinita de casos para demostrar una afirmación general, pero lo hace mediante una cadena finita de razonamiento deductivo que involucra la variable , que puede tomar una cantidad infinita de valores. El resultado es una prueba rigurosa de la afirmación, no una afirmación de su probabilidad. ^[4] ${\displaystyle n}$

Historia

En el año 370 a. C., el Parménides de Platón puede haber contenido rastros de un ejemplo temprano de una prueba inductiva implícita, ^[5] sin embargo, la prueba implícita más antigua por inducción matemática fue escrita por al-Karaji alrededor del año 1000 d. C., quien la aplicó a secuencias aritméticas para demostrar el teorema del binomio y las propiedades del triángulo de Pascal . Si bien la obra original se perdió, Al-Samawal al-Maghribi hizo referencia a ella más tarde en su tratado al-Bahir fi'l-jabr (El brillante en álgebra) alrededor del año 1150 d. C. ^{[6] [7]}

Katz dice en su historia de las matemáticas

Otra idea importante introducida por al-Karaji y continuada por al-Samaw'al y otros fue la de un argumento inductivo para tratar ciertas secuencias aritméticas. Así, al-Karaji utilizó tal argumento para probar el resultado sobre las sumas de cubos integrales ya conocidos por Aryabhata [...] Al-Karaji, sin embargo, no enunció un resultado general para un n arbitrario . Enunció su teorema para el entero particular 10 [...] Su prueba, sin embargo, fue claramente diseñada para ser extensible a cualquier otro entero. [...] El argumento de Al-Karaji incluye en esencia los dos componentes básicos de un argumento moderno por inducción, a saber, la verdad del enunciado para n = 1 (1 = 1 ³ ) y la derivación de la verdad para n = k a partir de la de n = k - 1. Por supuesto, este segundo componente no es explícito ya que, en cierto sentido, el argumento de al-Karaji es al revés; esto es, comienza desde n = 10 y baja hasta 1 en lugar de proceder hacia arriba. Sin embargo, su argumento en al-Fakhri es la prueba existente más antigua de la fórmula de suma para cubos integrales . ^[8]

En la India, las primeras pruebas implícitas por inducción matemática aparecen en el " método cíclico " de Bhaskara . ^[9]

Sin embargo, ninguno de estos matemáticos antiguos formuló explícitamente la hipótesis de la inducción. Otro caso similar (contrariamente a lo que escribió Vacca, como Freudenthal demostró cuidadosamente) ^[10] fue el de Francesco Maurolico en su Arithmeticorum libri duo (1575), quien utilizó la técnica para demostrar que la suma de los primeros n números enteros impares es n ² .

El primer uso riguroso de la inducción fue obra de Gersonides (1288-1344). ^{[11] [12]} La primera formulación explícita del principio de inducción fue dada por Pascal en su Traité du triangle arithmétique (1665). Otro francés, Fermat , hizo un amplio uso de un principio relacionado: la prueba indirecta por descendencia infinita .

La hipótesis de la inducción también fue empleada por el suizo Jakob Bernoulli , y desde entonces se hizo muy conocida. El tratamiento formal moderno del principio llegó recién en el siglo XIX, con George Boole , ^[13] Augustus De Morgan , Charles Sanders Peirce , ^{[14] [15]} Giuseppe Peano y Richard Dedekind . ^[9]

Descripción

La forma más simple y común de inducción matemática infiere que una afirmación que implica un número natural n (es decir, un entero n ≥ 0 o 1) es válida para todos los valores de n . La prueba consta de dos pasos:

1. Elcaso base (ocaso inicial): demostrar que la afirmación es válida para 0 o 1.
2. ElPaso de inducción (opaso inductivo, ocaso de paso): probar que para cadan, si el enunciado es válido paran, entonces es válido para n + 1.En otras palabras, supongamos que el enunciado es válido para un número natural arbitrarion, y probaremos que el enunciado es válido para n + 1.

La hipótesis del paso de inducción, de que el enunciado es válido para un valor n determinado , se denomina hipótesis de inducción o hipótesis inductiva . Para demostrar el paso de inducción, se supone la hipótesis de inducción para n y luego se utiliza esta suposición para demostrar que el enunciado es válido para n + 1 .

Los autores que prefieren definir los números naturales para que comiencen en 0 utilizan ese valor en el caso base; aquellos que definen los números naturales para que comiencen en 1 utilizan ese valor.

Ejemplos

Suma de números naturales consecutivos

La inducción matemática se puede utilizar para demostrar la siguiente afirmación P ( n ) para todos los números naturales n . $${\displaystyle P(n)\!:\ \ 0+1+2+\cdots +n={\frac {n(n+1)}{2}}.}$$

Esto establece una fórmula general para la suma de los números naturales menores o iguales a un número dado; de hecho, una secuencia infinita de afirmaciones: , , , etc. ${\displaystyle 0={\tfrac {(0)(0+1)}{2}}}$ ${\displaystyle 0+1={\tfrac {(1)(1+1)}{2}}}$ ${\displaystyle 0+1+2={\tfrac {(2)(2+1)}{2}}}$

Proposición. Para cada, ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle 0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.}$

Prueba. Sea P ( n ) el enunciado. Damos una prueba por inducción en n . ${\displaystyle 0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.}$

Caso base: Demuestre que la afirmación es válida para el número natural más pequeño n = 0 .

P (0) es claramente cierto: ${\displaystyle 0={\tfrac {0(0+1)}{2}}\,.}$

Paso de inducción: Demuestre que para cada k ≥ 0 , si P ( k ) se cumple, entonces P ( k + 1) también se cumple.

Supongamos la hipótesis de inducción de que para un k particular , se cumple el caso único n = k , lo que significa que P ( k ) es verdadero: Se deduce que: $${\displaystyle 0+1+\cdots +k={\frac {k(k+1)}{2}}.}$$ $${\displaystyle (0+1+2+\cdots +k)+(k+1)={\frac {k(k+1)}{2}}+(k+1).}$$

Algebraicamente , el lado derecho se simplifica como: $${\displaystyle {\begin{aligned}{\frac {k(k+1)}{2}}+(k+1)&={\frac {k(k+1)+2(k+1)}{2}}\\&={\frac {(k+1)(k+2)}{2}}\\&={\frac {(k+1)((k+1)+1)}{2}}.\end{aligned}}}$$

Igualando los extremos izquierdo y derecho, deducimos que: Es decir, la afirmación P ( k + 1) también es cierta, estableciendo el paso de inducción. $${\displaystyle 0+1+2+\cdots +k+(k+1)={\frac {(k+1)((k+1)+1)}{2}}.}$$

Conclusión: Dado que tanto el caso base como el paso de inducción han sido probados como verdaderos, por inducción matemática la afirmación P ( n ) es válida para cada número natural n . QED

Una desigualdad trigonométrica

La inducción se utiliza a menudo para demostrar desigualdades . Como ejemplo, demostramos que para cualquier número real y número natural . ${\displaystyle \left|\sin nx\right|\leq n\left|\sin x\right|}$ ${\displaystyle x}$ ${\displaystyle n}$

A primera vista, puede parecer que una versión más general, para cualquier número real , podría demostrarse sin inducción; pero el caso muestra que puede ser falsa para valores no enteros de . Esto sugiere que examinemos el enunciado específicamente para valores naturales de , y la inducción es la herramienta más disponible. ${\displaystyle \left|\sin nx\right|\leq n\left|\sin x\right|}$ ${\displaystyle n,x}$ ${\textstyle n={\frac {1}{2}},\,x=\pi }$ ${\displaystyle n}$ ${\displaystyle n}$

Proposición. Para cualquiery,. ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle \left|\sin nx\right|\leq n\left|\sin x\right|}$

Demostración. Fijemos un número real arbitrario y sea el enunciado . Inducimos en . ${\displaystyle x}$ ${\displaystyle P(n)}$ ${\displaystyle \left|\sin nx\right|\leq n\left|\sin x\right|}$ ${\displaystyle n}$

Caso base: El cálculo verifica . ${\displaystyle \left|\sin 0x\right|=0\leq 0=0\left|\sin x\right|}$ ${\displaystyle P(0)}$

Paso de inducción: Demostramos la implicación para cualquier número natural . Supongamos la hipótesis de inducción: para un valor dado , el único caso es verdadero. Utilizando la fórmula de la suma de ángulos y la desigualdad triangular , deducimos: ${\displaystyle P(k)\implies P(k+1)}$ ${\displaystyle k}$ ${\displaystyle n=k\geq 0}$ ${\displaystyle P(k)}$ $${\displaystyle {\begin{aligned}\left|\sin(k+1)x\right|&=\left|\sin kx\cos x+\sin x\cos kx\right|&&{\text{(angle addition)}}\\&\leq \left|\sin kx\cos x\right|+\left|\sin x\,\cos kx\right|&&{\text{(triangle inequality)}}\\&=\left|\sin kx\right|\left|\cos x\right|+\left|\sin x\right|\left|\cos kx\right|\\&\leq \left|\sin kx\right|+\left|\sin x\right|&&(\left|\cos t\right|\leq 1)\\&\leq k\left|\sin x\right|+\left|\sin x\right|&&{\text{(induction hypothesis}})\\&=(k+1)\left|\sin x\right|.\end{aligned}}}$$

La desigualdad entre las cantidades extremas de la izquierda y la derecha muestra que es verdadera, lo que completa el paso de inducción. ${\displaystyle P(k+1)}$

Conclusión: La proposición es válida para todos los números naturales QED ${\displaystyle P(n)}$ ${\displaystyle n.}$ 

Variantes

En la práctica, las demostraciones por inducción suelen estructurarse de forma diferente, dependiendo de la naturaleza exacta de la propiedad que se desea demostrar. Todas las variantes de inducción son casos especiales de inducción transfinita ; véase más abajo.

Caso base distinto de 0 o 1

Si se desea demostrar una afirmación, no para todos los números naturales, sino sólo para todos los números n mayores o iguales a un cierto número b , entonces la demostración por inducción consiste en lo siguiente:

1. Demostrando que la afirmación es válida cuando n = b .
2. Demostrando que si la afirmación es válida para un número arbitrario n ≥ b , entonces la misma afirmación también es válida para n + 1 .

Esto se puede utilizar, por ejemplo, para demostrar que 2 ⁿ ≥ n + 5 para n ≥ 3 .

De esta manera, se puede demostrar que alguna afirmación P ( n ) es válida para todo n ≥ 1 , o incluso para todo n ≥ −5 . Esta forma de inducción matemática es en realidad un caso especial de la forma anterior, porque si la afirmación a demostrar es P ( n ), entonces demostrarla con estas dos reglas es equivalente a demostrar P ( n + b ) para todos los números naturales n con un caso base de inducción 0 . ^[16]

Ejemplo: formación de cantidades en dólares a partir de monedas

Supongamos que hay un suministro infinito de monedas de 4 y 5 dólares. Se puede utilizar la inducción para demostrar que cualquier cantidad total de dólares mayor o igual a 12 se puede formar mediante una combinación de dichas monedas. Sea S ( k ) el enunciado " k dólares se pueden formar mediante una combinación de monedas de 4 y 5 dólares". La prueba de que S ( k ) es verdadera para todo k ≥ 12 se puede lograr entonces mediante inducción sobre k de la siguiente manera:

Caso base: demostrar que S ( k ) se cumple para k = 12 es simple: tome tres monedas de 4 dólares.

Paso de inducción: Dado que S ( k ) se cumple para algún valor de k ≥ 12 ( hipótesis de inducción ), demuestre que S ( k + 1) también se cumple. Suponga que S ( k ) es verdadera para algún valor arbitrario de k ≥ 12. Si hay una solución para k dólares que incluye al menos una moneda de 4 dólares, reemplácela por una moneda de 5 dólares para obtener k + 1 dólares. De lo contrario, si solo se usan monedas de 5 dólares, k debe ser un múltiplo de 5 y, por lo tanto, al menos 15; pero luego podemos reemplazar tres monedas de 5 dólares por cuatro monedas de 4 dólares para obtener k + 1 dólares. En cada caso, S ( k + 1) es verdadera.

Por lo tanto, por el principio de inducción, S ( k ) se cumple para todo k ≥ 12 , y la prueba está completa.

En este ejemplo, aunque S ( k ) también es válido para , la prueba anterior no se puede modificar para reemplazar la cantidad mínima de 12 dólares por cualquier valor inferior m . Para m = 11 , el caso base es en realidad falso; para m = 10 , el segundo caso en el paso de inducción (reemplazar tres monedas de 5 por cuatro de 4 dólares) no funcionará; y mucho menos para un valor m incluso inferior . ${\textstyle k\in \{4,5,8,9,10\}}$

Inducción en más de una encimera

A veces es deseable demostrar una afirmación que involucra dos números naturales, n y m , iterando el proceso de inducción. Es decir, se demuestra un caso base y un paso de inducción para n , y en cada uno de ellos se demuestra un caso base y un paso de inducción para m . Véase, por ejemplo, la prueba de conmutatividad que acompaña a la suma de números naturales . También son posibles argumentos más complicados que involucran tres o más contadores.

Descenso infinito

El método de descenso infinito es una variante de la inducción matemática utilizada por Pierre de Fermat . Se utiliza para demostrar que algún enunciado Q ( n ) es falso para todos los números naturales n . Su forma tradicional consiste en demostrar que si Q ( n ) es verdadero para algún número natural n , también es cierto para algún número natural estrictamente menor m . Como no hay sucesiones infinitas decrecientes de números naturales, esta situación sería imposible, demostrando así ( por contradicción ) que Q ( n ) no puede ser verdadero para ningún n .

La validez de este método puede verificarse a partir del principio habitual de inducción matemática. Aplicando la inducción matemática a la afirmación P ( n ) definida como " Q ( m ) es falsa para todos los números naturales m menores o iguales a n ", se deduce que P ( n ) es válida para todos los n , lo que significa que Q ( n ) es falsa para todo número natural n .

Inducción matemática limitada

Si se desea demostrar que una propiedad P se cumple para todos los números naturales menores o iguales a n , basta con demostrar que P satisface las siguientes condiciones: ^[17]

1. P se mantiene para 0,
2. Para cualquier número natural x menor que n , si P se cumple para x , entonces P se cumple para x + 1

Inducción de prefijos

La forma más común de prueba por inducción matemática requiere demostrar en el paso de inducción que $${\displaystyle \forall k\,(P(k)\to P(k+1))}$$

Con lo cual el principio de inducción "automatiza" n aplicaciones de este paso para pasar de P (0) a P ( n ) . Esto podría llamarse "inducción de predecesores" porque cada paso prueba algo sobre un número a partir de algo sobre el predecesor de ese número.

Una variante de interés en la complejidad computacional es la "inducción de prefijo", en la que se prueba la siguiente afirmación en el paso de inducción: o equivalentemente $${\displaystyle \forall k\,(P(k)\to P(2k)\land P(2k+1))}$$ $${\displaystyle \forall k\,\left(P\!\left(\left\lfloor {\frac {k}{2}}\right\rfloor \right)\to P(k)\right)}$$

El principio de inducción entonces "automatiza" las aplicaciones log ₂  n de esta inferencia para llegar de P (0) a P ( n ) . De hecho, se llama "inducción de prefijo" porque cada paso prueba algo sobre un número a partir de algo sobre el "prefijo" de ese número, tal como se forma al truncar el bit bajo de su representación binaria . También puede verse como una aplicación de la inducción tradicional sobre la longitud de esa representación binaria.

Si la inducción de predecesores tradicional se interpreta computacionalmente como un bucle de n pasos, entonces la inducción de prefijos correspondería a un bucle de log -n pasos. Por eso, las demostraciones que utilizan la inducción de prefijos son "más factibles y constructivas" que las demostraciones que utilizan la inducción de predecesores.

La inducción de predecesores puede simular trivialmente la inducción de prefijos en el mismo enunciado. La inducción de prefijos puede simular la inducción de predecesores, pero sólo a costa de hacer que el enunciado sea más complejo sintácticamente (añadiendo un cuantificador universal acotado ), por lo que los resultados interesantes que relacionan la inducción de prefijos con el cálculo en tiempo polinomial dependen de excluir por completo los cuantificadores no acotados y limitar la alternancia de cuantificadores universales acotados y existenciales permitidos en el enunciado. ^[18]

Se puede llevar la idea un paso más allá: hay que demostrar que el principio de inducción "automatiza" log log n las aplicaciones de esta inferencia para llegar de P (0) a P ( n ) . Esta forma de inducción se ha utilizado, de forma análoga, para estudiar el cálculo paralelo en tiempo logarítmico. ^{[ cita requerida ]} $${\displaystyle \forall k\,\left(P\!\left(\left\lfloor {\sqrt {k}}\right\rfloor \right)\to P(k)\right)}$$

Inducción completa (fuerte)

Otra variante, llamada inducción completa , inducción del curso de valores o inducción fuerte (en contraste con la cual la forma básica de inducción a veces se conoce como inducción débil ), hace que el paso de inducción sea más fácil de probar al usar una hipótesis más fuerte: uno prueba el enunciado bajo el supuesto de que se cumple para todos los números naturales menores que ; por el contrario, la forma básica solo supone . El nombre "inducción fuerte" no significa que este método pueda probar más que la "inducción débil", sino que simplemente se refiere a la hipótesis más fuerte utilizada en el paso de inducción. ${\displaystyle P(m+1)}$ ${\displaystyle P(n)}$ ${\displaystyle n}$ ${\displaystyle m+1}$ ${\displaystyle P(m)}$

De hecho, se puede demostrar que los dos métodos son equivalentes, como se explica a continuación. En esta forma de inducción completa, todavía hay que demostrar el caso base, , e incluso puede ser necesario demostrar casos extrabase, como por ejemplo antes de que se aplique el argumento general, como en el ejemplo siguiente del número de Fibonacci . ${\displaystyle P(0)}$ ${\displaystyle P(1)}$ ${\displaystyle F_{n}}$

Aunque la forma que se acaba de describir requiere que uno pruebe el caso base, esto es innecesario si uno puede probar (suponiendo para todos los ) para todos los . Este es un caso especial de inducción transfinita como se describe a continuación, aunque ya no es equivalente a la inducción ordinaria. En esta forma el caso base es subsumido por el caso , donde se prueba sin ningún otro supuesto; este caso puede necesitar ser manejado por separado, pero a veces el mismo argumento se aplica para y , haciendo que la prueba sea más simple y más elegante. En este método, sin embargo, es vital asegurar que la prueba de no suponga implícitamente que , por ejemplo diciendo "elige un arbitrario ", o suponiendo que un conjunto de m elementos tiene un elemento. ${\displaystyle P(m)}$ ${\displaystyle P(n)}$ ${\displaystyle n}$ ${\displaystyle m\geq 0}$ ${\displaystyle m=0}$ ${\displaystyle P(0)}$ ${\displaystyle P(n)}$ ${\displaystyle m=0}$ ${\displaystyle m>0}$ ${\displaystyle P(m)}$ ${\displaystyle m>0}$ ${\displaystyle n<m}$

Equivalencia con inducción ordinaria

La inducción completa es equivalente a la inducción matemática ordinaria como se describió anteriormente, en el sentido de que una prueba por un método puede transformarse en una prueba por el otro. Supongamos que hay una prueba de por inducción completa. Entonces, esta prueba puede transformarse en una prueba de inducción ordinaria asumiendo una hipótesis inductiva más fuerte. Sea la afirmación " se cumple para todos los tales que " - esta se convierte en la hipótesis inductiva para la inducción ordinaria. Podemos entonces demostrar y para suponer solo y demostrar que implica . ^[19] ${\displaystyle P(n)}$ ${\displaystyle Q(n)}$ ${\displaystyle P(m)}$ ${\displaystyle m}$ ${\displaystyle 0\leq m\leq n}$ ${\displaystyle Q(0)}$ ${\displaystyle Q(n+1)}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle Q(n)}$ ${\displaystyle Q(n)}$ ${\displaystyle P(n)}$

Si, por otra parte, se hubiera probado por inducción ordinaria, la prueba ya sería efectivamente una por inducción completa: se prueba en el caso base, sin usar suposiciones, y se prueba en el paso de inducción, en el que uno puede asumir todos los casos anteriores pero sólo necesita usar el caso . ${\displaystyle P(n)}$ ${\displaystyle P(0)}$ ${\displaystyle P(n+1)}$ ${\displaystyle P(n)}$

Ejemplo: Números de Fibonacci

La inducción completa es más útil cuando se requieren varias instancias de la hipótesis inductiva para cada paso de inducción. Por ejemplo, la inducción completa se puede utilizar para demostrar que donde es el n -ésimo número de Fibonacci , y (la proporción áurea ) y son las raíces del polinomio . Al utilizar el hecho de que para cada , la identidad anterior se puede verificar mediante un cálculo directo para si se supone que ya se cumple para ambos y . Para completar la prueba, la identidad debe verificarse en los dos casos base: y . $${\displaystyle F_{n}={\frac {\varphi ^{n}-\psi ^{n}}{\varphi -\psi }}}$$ ${\displaystyle F_{n}}$ ${\textstyle \varphi ={\frac {1}{2}}(1+{\sqrt {5}})}$ ${\textstyle \psi ={\frac {1}{2}}(1-{\sqrt {5}})}$ ${\displaystyle x^{2}-x-1}$ ${\displaystyle F_{n+2}=F_{n+1}+F_{n}}$ ${\displaystyle n\in \mathbb {N} }$ ${\textstyle F_{n+2}}$ ${\textstyle F_{n+1}}$ ${\textstyle F_{n}}$ ${\displaystyle n=0}$ ${\textstyle n=1}$

Ejemplo: factorización prima

Otra prueba por inducción completa utiliza la hipótesis de que el enunciado se cumple para todos los números más pequeños de manera más completa. Consideremos el enunciado de que "todo número natural mayor que 1 es un producto de (uno o más) números primos ", que es la parte de " existencia " del teorema fundamental de la aritmética . Para probar el paso de inducción, la hipótesis de inducción es que para un dado el enunciado se cumple para todos los números más pequeños . Si es primo, entonces es ciertamente un producto de primos, y si no, entonces por definición es un producto: , donde ninguno de los factores es igual a 1; por lo tanto, ninguno es igual a , y por lo tanto ambos son mayores que 1 y menores que . La hipótesis de inducción ahora se aplica a y , por lo que cada uno es un producto de primos. Por lo tanto, es un producto de productos de primos y, por lo tanto, por extensión, un producto de primos en sí mismo. ${\displaystyle n}$ ${\displaystyle n>1}$ ${\displaystyle n>1}$ ${\displaystyle m}$ ${\displaystyle m=n_{1}n_{2}}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle n_{1}}$ ${\displaystyle n_{2}}$ ${\displaystyle m}$

Ejemplo: montos en dólares revisados

Intentaremos demostrar el mismo ejemplo anterior, esta vez con inducción fuerte . La afirmación sigue siendo la misma: $${\displaystyle S(n):\,\,n\geq 12\implies \,\exists \,a,b\in \mathbb {N} .\,\,n=4a+5b}$$

Sin embargo, habrá ligeras diferencias en la estructura y los supuestos de la prueba, comenzando con el caso base extendido.

Prueba.

Caso base: Demuestre que esto es válido para . ${\displaystyle S(k)}$ ${\displaystyle k=12,13,14,15}$ $${\displaystyle {\begin{aligned}4\cdot 3+5\cdot 0=12\\4\cdot 2+5\cdot 1=13\\4\cdot 1+5\cdot 2=14\\4\cdot 0+5\cdot 3=15\end{aligned}}}$$

El caso base se mantiene.

Paso de inducción: Dado algún , suponga que se cumple para todos con . Pruebe que se cumple. ${\displaystyle j>15}$ ${\displaystyle S(m)}$ ${\displaystyle m}$ ${\displaystyle 12\leq m<j}$ ${\displaystyle S(j)}$

La elección de , y la observación de que muestra que se cumple, según la hipótesis inductiva. Es decir, la suma puede estar formada por alguna combinación de monedas de dólar y . Entonces, simplemente añadiendo una moneda de dólar a esa combinación se obtiene la suma . Es decir, se cumple ^[20] QED ${\displaystyle m=j-4}$ ${\displaystyle 15<j\implies 12\leq j-4<j}$ ${\displaystyle S(j-4)}$ ${\displaystyle j-4}$ ${\displaystyle 4}$ ${\displaystyle 5}$ ${\displaystyle 4}$ ${\displaystyle j}$ ${\displaystyle S(j)}$

Inducción hacia adelante y hacia atrás

A veces, es más conveniente deducir hacia atrás, demostrando la afirmación para , dada su validez para . Sin embargo, demostrar la validez de la afirmación para ningún número individual es suficiente para establecer el caso base; en cambio, es necesario demostrar la afirmación para un subconjunto infinito de los números naturales. Por ejemplo, Augustin Louis Cauchy utilizó primero la inducción hacia delante (regular) para demostrar la desigualdad de las medias aritmética y geométrica para todas las potencias de 2 , y luego utilizó la inducción hacia atrás para demostrarla para todos los números naturales. ^{[21] [22]} ${\displaystyle n-1}$ ${\displaystyle n}$

Ejemplo de error en el paso de inducción

El paso de inducción debe demostrarse para todos los valores de n . Para ilustrar esto, Joel E. Cohen propuso el siguiente argumento, que pretende demostrar por inducción matemática que todos los caballos son del mismo color : ^[23]

Caso base: en un conjunto de un solo caballo, solo hay un color.

Paso de inducción: supongamos como hipótesis de inducción que dentro de cualquier conjunto de caballos, hay un solo color. Ahora observemos cualquier conjunto de caballos. Numeremoslos: . Consideremos los conjuntos y . Cada uno es un conjunto de solo caballos, por lo tanto, dentro de cada uno hay un solo color. Pero los dos conjuntos se superponen, por lo que debe haber un solo color entre todos los caballos. ${\displaystyle n}$ ${\displaystyle n+1}$ ${\displaystyle 1,2,3,\dotsc ,n,n+1}$ ${\textstyle \left\{1,2,3,\dotsc ,n\right\}}$ ${\textstyle \left\{2,3,4,\dotsc ,n+1\right\}}$ ${\displaystyle n}$ ${\displaystyle n+1}$

El caso base es trivial y el paso de inducción es correcto en todos los casos . Sin embargo, el argumento utilizado en el paso de inducción es incorrecto para , porque la afirmación de que "los dos conjuntos se superponen" es falsa para y . ${\displaystyle n=1}$ ${\displaystyle n>1}$ ${\displaystyle n+1=2}$ ${\textstyle \left\{1\right\}}$ ${\textstyle \left\{2\right\}}$

Formalización

En lógica de segundo orden , uno puede escribir el " axioma de inducción" de la siguiente manera: donde P (·) es una variable para predicados que involucran un número natural y k y n son variables para números naturales . $${\displaystyle \forall P\,{\Bigl (}P(0)\land \forall k{\bigl (}P(k)\to P(k+1){\bigr )}\to \forall n\,{\bigl (}P(n){\bigr )}{\Bigr )},}$$

En palabras, el caso base P (0) y el paso de inducción (es decir, que la hipótesis de inducción P ( k ) implica P ( k + 1) ) juntos implican que P ( n ) para cualquier número natural n . El axioma de inducción afirma la validez de inferir que P ( n ) se cumple para cualquier número natural n a partir del caso base y el paso de inducción.

El primer cuantificador del axioma se aplica a predicados en lugar de a números individuales. Se trata de un cuantificador de segundo orden, lo que significa que este axioma se enuncia en lógica de segundo orden . Para axiomatizar la inducción aritmética en lógica de primer orden se requiere un esquema axiomático que contenga un axioma independiente para cada predicado posible. El artículo Axiomas de Peano contiene un análisis más detallado de esta cuestión.

El axioma de inducción estructural para los números naturales fue formulado por primera vez por Peano, quien lo utilizó para especificar los números naturales junto con los otros cuatro axiomas siguientes:

1. 0 es un número natural.
2. La función sucesora s de cada número natural produce un número natural ( s ( x ) = x + 1) .
3. La función sucesora es inyectiva .
4. 0 no está en el rango de s .

En la teoría de conjuntos de ZFC de primer orden , no se permite la cuantificación sobre predicados, pero aún se puede expresar la inducción por cuantificación sobre conjuntos: A puede leerse como un conjunto que representa una proposición y que contiene números naturales, para los cuales la proposición es válida. Esto no es un axioma, sino un teorema, dado que los números naturales se definen en el lenguaje de la teoría de conjuntos de ZFC por axiomas, análogos a los de Peano. Véase construcción de los números naturales usando el axioma de infinito y esquema axiomático de especificación . $${\displaystyle \forall A{\Bigl (}0\in A\land \forall k\in \mathbb {N} {\bigl (}k\in A\to (k+1)\in A{\bigr )}\to \mathbb {N} \subseteq A{\Bigr )}}$$

Inducción transfinita

Una variante del principio de inducción completa puede generalizarse para enunciados sobre elementos de cualquier conjunto bien fundado , es decir, un conjunto con una relación irreflexiva < que no contenga cadenas infinitas descendentes . Todo conjunto que represente un número ordinal es bien fundado, el conjunto de los números naturales es uno de ellos.

Aplicada a un conjunto bien fundado, la inducción transfinita puede formularse en un solo paso. Para demostrar que una afirmación P ( n ) es válida para cada número ordinal:

1. Demuestre, para cada número ordinal n , que si P ( m ) se cumple para todo m < n , entonces P ( n ) también se cumple.

Esta forma de inducción, cuando se aplica a un conjunto de números ordinales (que forman una clase bien ordenada y, por lo tanto, bien fundada ), se denomina inducción transfinita . Es una técnica de demostración importante en teoría de conjuntos , topología y otros campos.

Las pruebas por inducción transfinita suelen distinguir tres casos:

1. cuando n es un elemento mínimo, es decir, no hay ningún elemento menor que n ;
2. cuando n tiene un predecesor directo, es decir, el conjunto de elementos que son menores que n tiene un elemento mayor;
3. cuando n no tiene predecesor directo, es decir, n es un llamado ordinal límite .

Estrictamente hablando, en la inducción transfinita no es necesario demostrar un caso base, porque se trata de un caso especial vacuo de la proposición de que si P es verdadera para todos los n < m , entonces P es verdadera para m . Es vacuamente verdadera precisamente porque no hay valores de n < m que puedan servir como contraejemplos. Por lo tanto, los casos especiales son casos especiales del caso general.

Relación con el principio de buen orden

El principio de inducción matemática suele enunciarse como un axioma de los números naturales; véase Axiomas de Peano . Es estrictamente más fuerte que el principio de buen orden en el contexto de los demás axiomas de Peano. Supongamos lo siguiente:

• El axioma de tricotomía : Para cualesquiera números naturales n y m , n es menor o igual que m si y sólo si m no es menor que n .
• Para cualquier número natural n , n + 1 es mayor que n .
• Para cualquier número natural n , ningún número natural está entre n y n + 1 .
• Ningún número natural es menor que cero.

Se puede demostrar entonces que la inducción, dados los axiomas enumerados anteriormente, implica el principio de buen orden. La siguiente demostración utiliza la inducción completa y los axiomas primero y cuarto.

Demostración. Supóngase que existe un conjunto no vacío , S , de números naturales que no tiene ningún elemento mínimo. Sea P ( n ) la afirmación de que n no está en S . Entonces P (0) es verdadera, pues si fuera falsa entonces 0 es el elemento mínimo de S . Además, sea n un número natural, y supóngase que P ( m ) es verdadera para todos los números naturales m menores que n + 1 . Entonces si P ( n + 1) es falsa n + 1 está en S , siendo por tanto un elemento mínimo en S , una contradicción. Por tanto P ( n + 1) es verdadera. Por tanto, por el principio de inducción completa, P ( n ) se cumple para todos los números naturales n ; por tanto S está vacío, una contradicción. QED

" Recta numérica " ​​para el conjunto {(0, n ): n ∈ N } ∪ {(1, n ): n ∈ N } . Los números se refieren al segundo componente de los pares; el primero se puede obtener a partir del color o la ubicación.

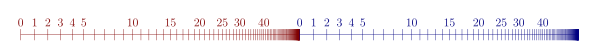
Por otra parte, el conjunto , mostrado en la imagen, está bien ordenado ^{[24] : 35lf} por el orden lexicográfico . Además, a excepción del axioma de inducción, satisface todos los axiomas de Peano, donde la constante de Peano 0 se interpreta como el par (0, 0), y la función sucesora de Peano se define en pares por succ( x , n ) = ( x , n + 1) para todos y . Como ejemplo de la violación del axioma de inducción, defina el predicado P ( x , n ) como ( x , n ) = (0, 0) o ( x , n ) = succ( y , m ) para algunos y . Entonces el caso base P (0, 0) es trivialmente verdadero, y también lo es el paso de inducción: si P ( x , n ) , entonces P (succ( x , n )) . Sin embargo, P no es verdadera para todos los pares del conjunto, ya que P (1,0) es falso. ${\displaystyle \{(0,n):n\in \mathbb {N} \}\cup \{(1,n):n\in \mathbb {N} \}}$ ${\displaystyle x\in \{0,1\}}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle y\in \{0,1\}}$ ${\displaystyle m\in \mathbb {N} }$

Los axiomas de Peano junto con el principio de inducción modelan de manera única los números naturales. Reemplazar el principio de inducción por el principio de buen orden permite modelos más exóticos que cumplen con todos los axiomas. ^[24]

En varios libros ^[24] y fuentes se publica erróneamente que el principio de buen orden es equivalente al axioma de inducción. En el contexto de los otros axiomas de Peano, este no es el caso, pero en el contexto de otros axiomas, son equivalentes; ^[24] específicamente, el principio de buen orden implica el axioma de inducción en el contexto de los dos primeros axiomas enumerados anteriormente y

• Todo número natural es 0 o n + 1 para algún número natural n .

Un error común en muchas pruebas erróneas es suponer que n − 1 es un número natural único y bien definido, una propiedad que no está implícita en los otros axiomas de Peano. ^[24]

Véase también

• Rompecabezas de inducción
• Prueba por agotamiento

Notas

1. Matt DeVos, Inducción matemática, Universidad Simon Fraser
2. Gerardo con Diaz, Inducción matemática Archivado el 2 de mayo de 2013 en Wayback Machine , Universidad de Harvard
3. Anderson, Robert B. (1979). Probando la corrección de los programas . Nueva York: John Wiley & Sons. pág. 1. ISBN 978-0471033950.
4. Suber, Peter. «Inducción matemática». Earlham College. Archivado desde el original el 24 de mayo de 2011. Consultado el 26 de marzo de 2011 .
5. Acerbi 2000.
6. Rashed 1994, págs. 62–84.
7. El conocimiento matemático y la interacción de las prácticas "La primera prueba implícita por inducción matemática fue dada alrededor del año 1000 en una obra del matemático persa Al-Karaji"
8. Katz (1998), pág. 255
9. Cajori (1918), p. 197: 'El proceso de razonamiento llamado "inducción matemática" ha tenido varios orígenes independientes. Se lo ha rastreado hasta el suizo Jakob (James) Bernoulli, los franceses B. Pascal y P. Fermat y el italiano F. Maurolycus. [...] Leyendo un poco entre líneas se pueden encontrar rastros de inducción matemática aún más antiguos, en los escritos de los hindúes y los griegos, como, por ejemplo, en el "método cíclico" de Bhaskara y en la prueba de Euclides de que el número de primos es infinito.'
10. Rashed 1994, pág. 62.
11. Simonson 2000.
12. Rabinovitch 1970.
13. "A veces se requiere demostrar un teorema que será verdadero siempre que una cierta cantidad n que involucra sea un entero o un número entero y el método de prueba es usualmente del siguiente tipo. 1º . El teorema se demuestra que es verdadero cuando n = 1. 2º . Se demuestra que si el teorema es verdadero cuando n es un número entero dado, será verdadero si n es el entero inmediatamente superior. Por lo tanto, el teorema es verdadero universalmente. … Esta especie de argumento puede ser denominada un sorites continuo " (Boole c. 1849 Tratado elemental de lógica no matemático pp. 40-41 reimpreso en Grattan-Guinness, Ivor y Bornet, Gérard (1997), George Boole: Selected Manuscripts on Logic and its Philosophy , Birkhäuser Verlag, Berlín, ISBN 3-7643-5456-9 ) 
14. Peirce 1881.
15. Escudos 1997.
16. Ted Sundstrom, Razonamiento matemático , pág. 190, Pearson, 2006, ISBN 978-0131877184 
17. Smullyan, Raymond (2014). Guía para principiantes de lógica matemática . Dover. pág. 41. ISBN 0486492370.
18. Buss, Samuel (1986). Aritmética limitada . Nápoles: Bibliopolis.
19. "Demostración: la inducción fuerte es equivalente a la inducción débil". Universidad de Cornell . Consultado el 4 de mayo de 2023 .
20. . Shafiei, Niloufar. "Inducción fuerte y buen orden" (PDF) . Universidad de York . Consultado el 28 de mayo de 2023 .
21. "Inducción hacia adelante y hacia atrás | Brilliant Math & Science Wiki". brilliant.org . Consultado el 23 de octubre de 2019 .
22. Cauchy, Augustin-Louis (1821). Cours d'analyse de l'École Royale Polytechnique, première partie, Analyse algébrique, Archivado el 14 de octubre de 2017 en Wayback Machine, París. La prueba de la desigualdad de las medias aritmética y geométrica se puede encontrar en las páginas 457 y siguientes.
23. Cohen, Joel E. (1961). "Sobre la naturaleza de la prueba matemática". Opus .. Reimpreso en Un paseo aleatorio en la ciencia (RL Weber, ed.), Crane, Russak & Co., 1973.
24. Öhman, Lars–Daniel (6 de mayo de 2019). "¿Son la inducción y el buen orden equivalentes?". The Mathematical Intelligencer . 41 (3): 33–40. doi : 10.1007/s00283-019-09898-4 .

Referencias

Introducción

• Franklin, J. y Daoud, A. (2011). Demostración en matemáticas: una introducción. Sydney: Kew Books. ISBN 978-0-646-54509-7.(Cap. 8.)
• "Inducción matemática". Enciclopedia de Matemáticas . EMS Press . 2001 [1994].
• Hermes, Hans (1973). Introducción a la lógica matemática . Hochschultext. Londres: Springer. ISBN 978-3540058199. ISSN  1431-4657. MR  0345788.
• Knuth, Donald E. (1997). El arte de la programación informática, volumen 1: Algoritmos fundamentales (3.ª ed.). Addison-Wesley. ISBN 978-0-201-89683-1.(Sección 1.2.1: Inducción matemática, págs. 11-21.)
• Kolmogorov, Andrey N. ; Fomin, Sergei V. (1975). Introducción al análisis real. Silverman, RA (trad., ed.). Nueva York: Dover. ISBN 978-0-486-61226-3.(Sección 3.8: Inducción transfinita, págs. 28-29.)

Historia

• Acerbi, Fabio (agosto de 2000). "Platón: Parménides 149a7-c3. ¿Una prueba por inducción completa?". Archivo de Historia de las Ciencias Exactas . 55 (1): 57–76. doi :10.1007/s004070000020. JSTOR  41134098. S2CID  123045154.
• Bussey, WH (1917). "El origen de la inducción matemática". The American Mathematical Monthly . 24 (5): 199–207. doi :10.2307/2974308. JSTOR  2974308.
• Cajori, Florian (1918). "Origen del nombre "Inducción matemática"". Revista Americana de Matemáticas . 25 (5): 197–201. doi :10.2307/2972638. JSTOR  2972638.
• Fowler, D. (1994). “¿Podrían los griegos haber utilizado la inducción matemática? ¿La utilizaron?”. Physis . 31 : 253–265.
• Freudenthal, Hans (1953). "Zur Geschichte der vollständigen Inducción". Archivos Internacionales de Historia de las Ciencias . 6 : 17–37.
• Katz, Victor J. (1998). Historia de las matemáticas: una introducción . Addison-Wesley . ISBN 0-321-01618-1.
• Peirce, Charles Sanders (1881). "Sobre la lógica de los números". American Journal of Mathematics . 4 (1–4): 85–95. doi :10.2307/2369151. JSTOR  2369151. MR  1507856.Reimpreso (CP 3.252–288), (W 4:299–309)
• Rabinovitch, Nachum L. (1970). "El rabino Levi Ben Gershon y los orígenes de la inducción matemática". Archivo de Historia de las Ciencias Exactas . 6 (3): 237–248. doi :10.1007/BF00327237. MR  1554128. S2CID  119948133.
• Rashed, Roshdi (1972). «L'induction mathématique: al-Karajī, as-Samaw'al». Archivo de Historia de las Ciencias Exactas (en francés). 9 (1): 1–21. doi :10.1007/BF00348537. MR  1554160. S2CID  124040444.
• Rashed, R. (1994). "Inducción matemática: al-Karajī y al-Samawʾal". El desarrollo de las matemáticas árabes: entre la aritmética y el álgebra. Boston Studies in the Philosophy of Science. Vol. 156. Springer Science & Business Media. ISBN 9780792325659.
• Shields, Paul (1997). "Axiomatización de la aritmética de Peirce". En Houser, Nathan; Roberts, Don D.; Evra, James Van (eds.). Estudios sobre la lógica de Charles S. Peirce . Indiana University Press. págs. 43–52. ISBN 0-253-33020-3.Señor 1720827  .
• Simonson, Charles G. (invierno de 2000). "Las matemáticas de Levi ben Gershon, el Ralbag" (PDF) . Bekhol Derakhekha Daehu . 10. Bar-Ilan University Press: 5–21.
• Unguru, S. (1991). "Matemáticas griegas e inducción matemática". Physis . 28 : 273–289.
• Unguru, S. (1994). "Cazar después de la inducción". Física . 31 : 267–272.
• Vacca, G. (1909). "Maurolycus, el primer descubridor del principio de inducción matemática". Boletín de la Sociedad Matemática Americana . 16 (2): 70–73. doi : 10.1090/S0002-9904-1909-01860-9 . MR  1558845.
• Yadegari, Mohammad (1978). "El uso de la inducción matemática por Abū Kāmil Shujā' Ibn Aslam (850-930)". Isis . 69 (2): 259–262. doi :10.1086/352009. JSTOR  230435. S2CID  144112534.