Teoría del haz de Euler-Bernoulli

Método para el cálculo de carga en construcción.

Esta viga de vidrio vibrante se puede modelar como una viga en voladizo con aceleración, densidad lineal variable, módulo de sección variable, algún tipo de disipación, carga elástica en el extremo y posiblemente una masa puntual en el extremo libre.

La teoría de vigas de Euler-Bernoulli (también conocida como teoría de vigas de ingeniero o teoría clásica de vigas ) ^[1] es una simplificación de la teoría lineal de la elasticidad que proporciona un medio para calcular las características de deflexión y carga de las vigas . Cubre el caso correspondiente a pequeñas deflexiones de una viga que está sometida únicamente a cargas laterales. Al ignorar los efectos de la deformación por corte y la inercia rotatoria, se trata de un caso especial de la teoría de vigas de Timoshenko-Ehrenfest . Fue enunciado por primera vez alrededor de 1750, ^[2] pero no se aplicó a gran escala hasta el desarrollo de la Torre Eiffel y la noria a finales del siglo XIX. Tras estas demostraciones exitosas, rápidamente se convirtió en una piedra angular de la ingeniería y un facilitador de la Segunda Revolución Industrial .

Se han desarrollado modelos matemáticos adicionales , como la teoría de placas , pero la simplicidad de la teoría de vigas la convierte en una herramienta importante en las ciencias, especialmente en la ingeniería estructural y mecánica .

Historia

Esquema de la sección transversal de una viga doblada que muestra el eje neutro.

El consenso predominante es que Galileo Galilei hizo los primeros intentos de desarrollar una teoría de los haces, pero estudios recientes sostienen que Leonardo da Vinci fue el primero en hacer las observaciones cruciales. Da Vinci carecía de la ley de Hooke y del cálculo para completar la teoría, mientras que Galileo se vio frenado por una suposición incorrecta que hizo. ^[3]

La viga Bernoulli lleva el nombre de Jacob Bernoulli , quien realizó importantes descubrimientos. Leonhard Euler y Daniel Bernoulli fueron los primeros en elaborar una teoría útil alrededor de 1750. ^[4]

Ecuación de haz estático

La ecuación de Euler-Bernoulli describe la relación entre la deflexión de la viga y la carga aplicada: ^[5]

${\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,}$

La curva describe la deflexión de la viga en la dirección en alguna posición (recuerde que la viga se modela como un objeto unidimensional). es una carga distribuida, en otras palabras, una fuerza por unidad de longitud (análoga a que la presión es una fuerza por área); puede ser una función de , u otras variables. es el módulo de elasticidad y es el segundo momento del área de la sección transversal de la viga. debe calcularse con respecto al eje que es perpendicular a la carga aplicada. ^{[N 1]} Explícitamente, para una viga cuyo eje está orientado con una carga a lo largo de , la sección transversal de la viga está en el plano y el segundo momento de área relevante es ${\displaystyle w(x)}$ ${\displaystyle z}$ ${\displaystyle x}$ ${\displaystyle q}$ ${\displaystyle x}$ ${\displaystyle w}$ ${\displaystyle E}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle x}$ ${\displaystyle z}$ ${\displaystyle yz}$

${\displaystyle I=\iint z^{2}\;dy\;dz,}$

donde se supone que el centroide de la sección transversal ocurre en . ${\displaystyle y=z=0}$

A menudo, el producto (conocido como rigidez a la flexión ) es una constante, de modo que ${\displaystyle EI}$

${\displaystyle EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=q(x).\,}$

Esta ecuación, que describe la deflexión de una viga estática uniforme, se utiliza ampliamente en la práctica de la ingeniería. Las expresiones tabuladas para la deflexión para configuraciones de vigas comunes se pueden encontrar en los manuales de ingeniería. Para situaciones más complicadas, la deflexión se puede determinar resolviendo la ecuación de Euler-Bernoulli utilizando técnicas como " integración directa ", " método de Macaulay ", " método de momento y área ", " método de viga conjugada ", " principio de trabajo virtual ", " método de Castigliano ", " método de flexibilidad ", " método de deflexión de pendiente ", " método de distribución de momentos " o " método de rigidez directa ". ${\displaystyle w}$

Las convenciones de signos se definen aquí ya que se pueden encontrar diferentes convenciones en la literatura. ^[5] En este artículo, se utiliza un sistema de coordenadas diestro con el eje hacia la derecha, el eje apuntando hacia arriba y el eje apuntando hacia dentro de la figura. El signo del momento flector se toma como positivo cuando el vector de torsión asociado al momento flector en el lado derecho de la sección es en dirección positiva, es decir, un valor positivo de produce tensión de compresión en la superficie inferior. Con esta elección de convención de signos de momento flector, para tener , es necesario que la fuerza cortante que actúa en el lado derecho de la sección sea positiva en la dirección para lograr el equilibrio estático de momentos. Si la intensidad de carga se toma positiva en la dirección positiva, entonces es necesaria para el equilibrio de fuerzas. ${\displaystyle x}$ ${\displaystyle z}$ ${\displaystyle y}$ ${\displaystyle M}$ ${\displaystyle y}$ ${\displaystyle M}$ ${\displaystyle dM=Qdx}$ ${\displaystyle Q}$ ${\displaystyle z}$ ${\displaystyle q}$ ${\displaystyle z}$ ${\displaystyle dQ=-qdx}$

Las sucesivas derivadas de la deflexión tienen importantes significados físicos: es la pendiente de la viga, que es el ángulo de rotación en sentido antihorario alrededor del eje - en el límite de pequeños desplazamientos; ${\displaystyle w}$ ${\displaystyle dw/dx}$ ${\displaystyle y}$

${\displaystyle M=-EI{\frac {d^{2}w}{dx^{2}}}}$

es el momento flector en la viga; y

${\displaystyle Q=-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}$

es la fuerza cortante en la viga.

Flexión de una viga de Euler-Bernoulli. Cada sección transversal de la viga está a 90 grados con respecto al eje neutro.

Las tensiones en una viga se pueden calcular a partir de las expresiones anteriores después de que se haya determinado la deflexión debida a una carga determinada.

Derivación de la ecuación de flexión.

Debido a la importancia fundamental de la ecuación del momento flector en ingeniería, proporcionaremos una breve derivación. Cambiamos a coordenadas polares. La longitud del eje neutro en la figura es La longitud de una fibra con una distancia radial por debajo del eje neutro es Por lo tanto, la deformación de esta fibra es ${\displaystyle \rho d\theta .}$ ${\displaystyle z}$ ${\displaystyle (\rho +z)d\theta .}$

${\displaystyle {\frac {\left(\rho +z-\rho \right)\ d\theta }{\rho \ d\theta }}={\frac {z}{\rho }}.}$

La tensión de esta fibra es donde está el módulo elástico de acuerdo con la Ley de Hooke . El vector de fuerza diferencial, resultante de esta tensión, viene dado por, ${\displaystyle E{\dfrac {z}{\rho }}}$ ${\displaystyle E}$ ${\displaystyle d\mathbf {F} ,}$

${\displaystyle d\mathbf {F} =E{\frac {z}{\rho }}dA\mathbf {e_{x}} .}$

Este es el vector de fuerza diferencial ejercido en el lado derecho de la sección que se muestra en la figura. Sabemos que es en la dirección ya que la figura muestra claramente que las fibras de la mitad inferior están en tensión. es el elemento diferencial del área en la ubicación de la fibra. El vector de momento flector diferencial, asociado con está dado por ${\displaystyle \mathbf {e_{x}} }$ ${\displaystyle dA}$ ${\displaystyle d\mathbf {M} }$ ${\displaystyle d\mathbf {F} }$

${\displaystyle d\mathbf {M} =-z\mathbf {e_{z}} \times d\mathbf {F} =-\mathbf {e_{y}} E{\frac {z^{2}}{\rho }}dA.}$

Esta expresión es válida para las fibras de la mitad inferior de la viga. La expresión para las fibras en la mitad superior de la viga será similar excepto que el vector del brazo de momento estará en la dirección positiva y el vector de fuerza estará en la dirección en que las fibras superiores están en compresión. Pero el vector de momento flector resultante seguirá estando en la dirección ya que , por lo tanto, integramos sobre toda la sección transversal de la viga y obtenemos para el vector de momento flector ejercido en la sección transversal derecha de la viga la expresión ${\displaystyle z}$ ${\displaystyle -x}$ ${\displaystyle -y}$ ${\displaystyle \mathbf {e_{z}} \times -\mathbf {e_{x}} =-\mathbf {e_{y}} .}$ ${\displaystyle \mathbf {M} }$

${\displaystyle \mathbf {M} =\int d\mathbf {M} =-\mathbf {e_{y}} {\frac {E}{\rho }}\int {z^{2}}\ dA=-\mathbf {e_{y}} {\frac {EI}{\rho }},}$

¿ Dónde está el segundo momento del área ? Por cálculo, sabemos que cuando es pequeño, como lo es para una viga de Euler-Bernoulli, podemos hacer la aproximación , donde es el radio de curvatura . Por lo tanto, ${\displaystyle I}$ ${\displaystyle {\dfrac {dw}{dx}}}$ ${\displaystyle {\dfrac {1}{\rho }}\simeq {\dfrac {d^{2}w}{dx^{2}}}}$ ${\displaystyle \rho }$

${\displaystyle \mathbf {M} =-\mathbf {e_{y}} EI{d^{2}w \over dx^{2}}.}$

Esta ecuación vectorial se puede separar en la definición del vector unitario de flexión ( está orientada como ) y en la ecuación de flexión: ${\displaystyle M}$ ${\displaystyle \mathbf {e_{y}} }$

${\displaystyle M=-EI{d^{2}w \over dx^{2}}.}$

Ecuación de haz dinámico

Modelo del método de elementos finitos de una vibración de una viga de ala ancha ( viga I ).

La ecuación del haz dinámico es la ecuación de Euler-Lagrange para la siguiente acción

${\displaystyle S=\int _{t_{1}}^{t_{2}}\int _{0}^{L}\left[{\frac {1}{2}}\mu \left({\frac {\partial w}{\partial t}}\right)^{2}-{\frac {1}{2}}EI\left({\frac {\partial ^{2}w}{\partial x^{2}}}\right)^{2}+q(x)w(x,t)\right]dxdt.}$

El primer término representa la energía cinética donde es la masa por unidad de longitud, el segundo término representa la energía potencial debida a fuerzas internas (cuando se considera con signo negativo), y el tercer término representa la energía potencial debida a la carga externa . La ecuación de Euler-Lagrange se utiliza para determinar la función que minimiza el funcional . Para una viga dinámica de Euler-Bernoulli, la ecuación de Euler-Lagrange es ${\displaystyle \mu }$ ${\displaystyle q(x)}$ ${\displaystyle S}$

${\displaystyle {\cfrac {\partial ^{2}}{\partial x^{2}}}\left(EI{\cfrac {\partial ^{2}w}{\partial x^{2}}}\right)=-\mu {\cfrac {\partial ^{2}w}{\partial t^{2}}}+q(x).}$

Cuando la viga es homogénea y son independientes de , y la ecuación de la viga es más simple: ${\displaystyle E}$ ${\displaystyle I}$ ${\displaystyle x}$

${\displaystyle EI{\cfrac {\partial ^{4}w}{\partial x^{4}}}=-\mu {\cfrac {\partial ^{2}w}{\partial t^{2}}}+q\,.}$

Vibración libre

En ausencia de una carga transversal, tenemos la ecuación de vibración libre . Esta ecuación se puede resolver usando una descomposición de Fourier del desplazamiento en la suma de vibraciones armónicas de la forma ${\displaystyle q}$

${\displaystyle w(x,t)={\text{Re}}[{\hat {w}}(x)~e^{-i\omega t}]}$

¿ Dónde está la frecuencia de vibración? Entonces, para cada valor de frecuencia, podemos resolver una ecuación diferencial ordinaria ${\displaystyle \omega }$

${\displaystyle EI~{\cfrac {\mathrm {d} ^{4}{\hat {w}}}{\mathrm {d} x^{4}}}-\mu \omega ^{2}{\hat {w}}=0\,.}$

La solución general de la ecuación anterior es

${\displaystyle {\hat {w}}=A_{1}\cosh(\beta x)+A_{2}\sinh(\beta x)+A_{3}\cos(\beta x)+A_{4}\sin(\beta x)\quad {\text{with}}\quad \beta :=\left({\frac {\mu \omega ^{2}}{EI}}\right)^{1/4}}$

¿ Dónde están las constantes? Estas constantes son únicas para un conjunto dado de condiciones de contorno. Sin embargo, la solución para el desplazamiento no es única y depende de la frecuencia. Estas soluciones generalmente se escriben como ${\displaystyle A_{1},A_{2},A_{3},A_{4}}$

${\displaystyle {\hat {w}}_{n}=A_{1}\cosh(\beta _{n}x)+A_{2}\sinh(\beta _{n}x)+A_{3}\cos(\beta _{n}x)+A_{4}\sin(\beta _{n}x)\quad {\text{with}}\quad \beta _{n}:=\left({\frac {\mu \omega _{n}^{2}}{EI}}\right)^{1/4}\,.}$

Las cantidades se denominan frecuencias naturales del haz. Cada una de las soluciones de desplazamiento se llama moda y la forma de la curva de desplazamiento se llama forma moda . ${\displaystyle \omega _{n}}$

Ejemplo: viga en voladizo

Formas modales para los primeros cuatro modos de una viga en voladizo vibrante.

Las condiciones de contorno para una viga en voladizo de longitud (fijada en ) son ${\displaystyle L}$ ${\displaystyle x=0}$

${\displaystyle {\begin{aligned}&{\hat {w}}_{n}=0~,~~{\frac {d{\hat {w}}_{n}}{dx}}=0\quad {\text{at}}~~x=0\\&{\frac {d^{2}{\hat {w}}_{n}}{dx^{2}}}=0~,~~{\frac {d^{3}{\hat {w}}_{n}}{dx^{3}}}=0\quad {\text{at}}~~x=L\,.\end{aligned}}}$

Si aplicamos estas condiciones, se encuentra que existen soluciones no triviales sólo si esta ecuación no lineal se puede resolver numéricamente. Las primeras cuatro raíces son , , y . ${\displaystyle \cosh(\beta _{n}L)\,\cos(\beta _{n}L)+1=0\,.}$ ${\displaystyle \beta _{1}L=0.596864\pi }$ ${\displaystyle \beta _{2}L=1.49418\pi }$ ${\displaystyle \beta _{3}L=2.50025\pi }$ ${\displaystyle \beta _{4}L=3.49999\pi }$

Las correspondientes frecuencias naturales de vibración son

${\displaystyle \omega _{1}=\beta _{1}^{2}{\sqrt {\frac {EI}{\mu }}}={\frac {3.5160}{L^{2}}}{\sqrt {\frac {EI}{\mu }}}~,~~\dots }$

Las condiciones de contorno también se pueden utilizar para determinar las formas modales a partir de la solución para el desplazamiento:

${\displaystyle {\hat {w}}_{n}=A_{1}\left[(\cosh \beta _{n}x-\cos \beta _{n}x)+{\frac {\cos \beta _{n}L+\cosh \beta _{n}L}{\sin \beta _{n}L+\sinh \beta _{n}L}}(\sin \beta _{n}x-\sinh \beta _{n}x)\right]}$

Haz en voladizo excitado cerca de la frecuencia de resonancia del modo 2.

La constante desconocida (en realidad constantes ya que hay una para cada ), que en general es compleja, está determinada por las condiciones iniciales de velocidad y desplazamientos del haz. Normalmente se utiliza un valor de al trazar formas de modo. Las soluciones al problema de las fuerzas no amortiguadas tienen desplazamientos ilimitados cuando la frecuencia de conducción coincide con una frecuencia natural , es decir, el haz puede resonar . Por tanto, las frecuencias naturales de un haz corresponden a las frecuencias a las que puede producirse la resonancia . ${\displaystyle n}$ ${\displaystyle A_{1}}$ ${\displaystyle t=0}$ ${\displaystyle A_{1}=1}$ ${\displaystyle \omega _{n}}$

Ejemplo: viga libre-libre (sin apoyo)

Los primeros cuatro modos de un haz de Euler-Bernoulli libre-libre vibrante.

Una viga libre-libre es una viga sin soportes. ^[6] Las condiciones de contorno para una viga libre-libre de longitud que se extiende desde hasta están dadas por: ${\displaystyle L}$ ${\displaystyle x=0}$ ${\displaystyle x=L}$

${\displaystyle {\frac {d^{2}{\hat {w}}_{n}}{dx^{2}}}=0~,~~{\frac {d^{3}{\hat {w}}_{n}}{dx^{3}}}=0\quad {\text{at}}~~x=0\,{\text{and}}\,x=L\,.}$

Si aplicamos estas condiciones, se encontrará que existen soluciones no triviales sólo si

${\displaystyle \cosh(\beta _{n}L)\,\cos(\beta _{n}L)-1=0\,.}$

Esta ecuación no lineal se puede resolver numéricamente. Las primeras cuatro raíces son , , y . ${\displaystyle \beta _{1}L=1.50562\pi }$ ${\displaystyle \beta _{2}L=2.49975\pi }$ ${\displaystyle \beta _{3}L=3.50001\pi }$ ${\displaystyle \beta _{4}L=4.50000\pi }$

Las correspondientes frecuencias naturales de vibración son:

${\displaystyle \omega _{1}=\beta _{1}^{2}{\sqrt {\frac {EI}{\mu }}}={\frac {22.3733}{L^{2}}}{\sqrt {\frac {EI}{\mu }}}~,~~\dots }$

Las condiciones de contorno también se pueden utilizar para determinar las formas modales a partir de la solución para el desplazamiento:

${\displaystyle {\hat {w}}_{n}=A_{1}{\Bigl [}(\cos \beta _{n}x+\cosh \beta _{n}x)-{\frac {\cos \beta _{n}L-\cosh \beta _{n}L}{\sin \beta _{n}L-\sinh \beta _{n}L}}(\sin \beta _{n}x+\sinh \beta _{n}x){\Bigr ]}}$

Al igual que con la viga en voladizo, las constantes desconocidas están determinadas por las condiciones iniciales de la velocidad y los desplazamientos de la viga. Además, las soluciones al problema forzado no amortiguado tienen desplazamientos ilimitados cuando la frecuencia de conducción coincide con una frecuencia natural . ${\displaystyle t=0}$ ${\displaystyle \omega _{n}}$

Estrés

Además de la deflexión, la ecuación de la viga describe fuerzas y momentos y, por lo tanto, puede usarse para describir tensiones . Por esta razón, la ecuación de vigas de Euler-Bernoulli se usa ampliamente en ingeniería , especialmente civil y mecánica, para determinar la resistencia (así como la deflexión) de vigas sometidas a flexión.

Tanto el momento flector como la fuerza cortante provocan tensiones en la viga. El esfuerzo debido a la fuerza cortante es máximo a lo largo del eje neutro de la viga (cuando el ancho de la viga, t, es constante a lo largo de la sección transversal de la viga; de lo contrario, es necesario evaluar una integral que incluya el primer momento y el ancho de la viga). para la sección transversal particular), y el esfuerzo de tracción máximo se encuentra en la superficie superior o inferior. Por tanto, el esfuerzo principal máximo en la viga puede no estar ni en la superficie ni en el centro, sino en algún área general. Sin embargo, las tensiones de fuerza cortante son insignificantes en comparación con las tensiones de momento flector en todas las vigas excepto en las más robustas, además del hecho de que las concentraciones de tensión comúnmente ocurren en las superficies, lo que significa que es probable que la tensión máxima en una viga esté en la superficie.

Doblado simple o simétrico

Elemento de una viga doblada: las fibras forman arcos concéntricos, las fibras superiores se comprimen y las inferiores se estiran.

Para secciones transversales de vigas que son simétricas con respecto a un plano perpendicular al plano neutro, se puede demostrar que el esfuerzo de tracción experimentado por la viga se puede expresar como:

${\displaystyle \sigma ={\frac {Mz}{I}}=-zE~{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}.\,}$

Aquí, está la distancia desde el eje neutral hasta un punto de interés; y es el momento flector. Tenga en cuenta que esta ecuación implica que la flexión pura (de signo positivo) causará tensión cero en el eje neutro, tensión positiva (de tracción) en la "parte superior" de la viga y tensión negativa (de compresión) en la parte inferior de la viga; y también implica que la tensión máxima estará en la superficie superior y la mínima en la inferior. Esta tensión de flexión puede superponerse a tensiones aplicadas axialmente, lo que provocará un desplazamiento en el eje neutro (esfuerzo cero). ${\displaystyle z}$ ${\displaystyle M}$

Esfuerzos máximos en una sección transversal.

Cantidades utilizadas en la definición del módulo de sección de una viga.

El esfuerzo máximo de tracción en una sección transversal está en el lugar y el esfuerzo máximo de compresión está en el lugar donde la altura de la sección transversal es . Estas tensiones son ${\displaystyle z=c_{1}}$ ${\displaystyle z=-c_{2}}$ ${\displaystyle h=c_{1}+c_{2}}$

${\displaystyle \sigma _{1}={\cfrac {Mc_{1}}{I}}={\cfrac {M}{S_{1}}}~;~~\sigma _{2}=-{\cfrac {Mc_{2}}{I}}=-{\cfrac {M}{S_{2}}}}$

Las cantidades son los módulos de sección ^[5] y se definen como ${\displaystyle S_{1},S_{2}}$

${\displaystyle S_{1}={\cfrac {I}{c_{1}}}~;~~S_{2}={\cfrac {I}{c_{2}}}}$

El módulo de sección combina toda la información geométrica importante sobre la sección de una viga en una sola cantidad. Para el caso en el que una viga es doblemente simétrica y tenemos un módulo de sección . ${\displaystyle c_{1}=c_{2}}$ ${\displaystyle S=I/c}$

Deformación en una viga de Euler-Bernoulli

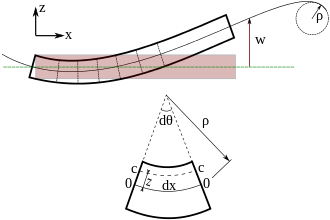
Necesitamos una expresión para la deformación en términos de la deflexión de la superficie neutra para relacionar las tensiones en una viga de Euler-Bernoulli con la deflexión. Para obtener esa expresión utilizamos el supuesto de que las normales a la superficie neutra permanecen normales durante la deformación y que las deflexiones son pequeñas. Estas suposiciones implican que la viga se dobla formando un arco de círculo de radio (ver Figura 1) y que la superficie neutra no cambia de longitud durante la deformación. ^[5] ${\displaystyle \rho }$

Sea la longitud de un elemento de la superficie neutra en estado no deformado. Para deflexiones pequeñas, el elemento no cambia su longitud después de doblarse, sino que se deforma en un arco de círculo de radio . Si es el ángulo subtendido por este arco, entonces . ${\displaystyle \mathrm {d} x}$ ${\displaystyle \rho }$ ${\displaystyle \mathrm {d} \theta }$ ${\displaystyle \mathrm {d} x=\rho ~\mathrm {d} \theta }$

Consideremos ahora otro segmento del elemento a una distancia por encima de la superficie neutra. La longitud inicial de este elemento es . Sin embargo, después de doblarlo, la longitud del elemento se vuelve . La deformación en ese segmento de la viga está dada por ${\displaystyle z}$ ${\displaystyle \mathrm {d} x}$ ${\displaystyle \mathrm {d} x'=(\rho -z)~\mathrm {d} \theta =\mathrm {d} x-z~\mathrm {d} \theta }$

${\displaystyle \varepsilon _{x}={\cfrac {\mathrm {d} x'-\mathrm {d} x}{\mathrm {d} x}}=-{\cfrac {z}{\rho }}=-\kappa ~z}$

¿ Dónde está la curvatura de la viga? Esto nos da la deformación axial en la viga en función de la distancia desde la superficie neutra. Sin embargo, todavía necesitamos encontrar una relación entre el radio de curvatura y la deflexión del haz . ${\displaystyle \kappa }$ ${\displaystyle w}$

Relación entre curvatura y deflexión del haz.

Sea P un punto sobre la superficie neutra de la viga a una distancia del origen del sistema de coordenadas. La pendiente del haz es aproximadamente igual al ángulo que forma la superficie neutra con el eje para los ángulos pequeños que se encuentran en la teoría de haces. Por lo tanto, con esta aproximación, ${\displaystyle x}$ ${\displaystyle (x,z)}$ ${\displaystyle x}$

${\displaystyle \theta (x)={\cfrac {\mathrm {d} w}{\mathrm {d} x}}}$

Por lo tanto, para un elemento infinitesimal , la relación se puede escribir como ${\displaystyle \mathrm {d} x}$ ${\displaystyle \mathrm {d} x=\rho ~\mathrm {d} \theta }$

${\displaystyle {\cfrac {1}{\rho }}={\cfrac {\mathrm {d} \theta }{\mathrm {d} x}}={\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}=\kappa }$

Por tanto, la deformación en la viga se puede expresar como

${\displaystyle \varepsilon _{x}=-z\kappa }$

Relaciones tensión-tensión

Para un material elástico lineal isotrópico homogéneo , la tensión está relacionada con la deformación por , donde es el módulo de Young . Por tanto, la tensión en una viga de Euler-Bernoulli viene dada por ${\displaystyle \sigma =E\varepsilon }$ ${\displaystyle E}$

${\displaystyle \sigma _{x}=-zE{\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}$

Tenga en cuenta que la relación anterior, en comparación con la relación entre el esfuerzo axial y el momento flector, conduce a

${\displaystyle M=-EI{\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}$

Como la fuerza cortante está dada por , también tenemos ${\displaystyle Q=\mathrm {d} M/\mathrm {d} x}$

${\displaystyle Q=-EI{\cfrac {\mathrm {d} ^{3}w}{\mathrm {d} x^{3}}}}$

Consideraciones de límites

La ecuación de la viga contiene una derivada de cuarto orden en . Para encontrar una solución única necesitamos cuatro condiciones de contorno. Las condiciones de contorno generalmente modelan apoyos , pero también pueden modelar cargas puntuales, cargas distribuidas y momentos. Las condiciones de contorno de apoyo o desplazamiento se utilizan para fijar valores de desplazamiento ( ) y rotaciones ( ) en el límite. Estas condiciones de frontera también se denominan condiciones de frontera de Dirichlet . Las condiciones de contorno de carga y momento implican derivadas más altas y representan el flujo de momento . Las condiciones de frontera de flujo también se denominan condiciones de frontera de Neumann . ${\displaystyle x}$ ${\displaystyle w(x,t)}$ ${\displaystyle w}$ ${\displaystyle \mathrm {d} w/\mathrm {d} x}$ ${\displaystyle w}$

Como ejemplo, considere una viga en voladizo que está incorporada en un extremo y libre en el otro, como se muestra en la figura adyacente. En el extremo incorporado de la viga no puede haber ningún desplazamiento o rotación de la viga. Esto significa que en el extremo izquierdo tanto la deflexión como la pendiente son cero. Como no se aplica ningún momento flector externo en el extremo libre de la viga, el momento flector en ese lugar es cero. Además, si no se aplica ninguna fuerza externa a la viga, la fuerza cortante en el extremo libre también es cero.

Tomando la coordenada del extremo izquierdo como y del extremo derecho como (la longitud de la viga), estas declaraciones se traducen en el siguiente conjunto de condiciones de contorno (supongamos que es una constante): ${\displaystyle x}$ ${\displaystyle 0}$ ${\displaystyle L}$ ${\displaystyle EI}$

Una viga en voladizo.

${\displaystyle w|_{x=0}=0\quad ;\quad {\frac {\partial w}{\partial x}}{\bigg |}_{x=0}=0\qquad {\mbox{(fixed end)}}\,}$

${\displaystyle {\frac {\partial ^{2}w}{\partial x^{2}}}{\bigg |}_{x=L}=0\quad ;\quad {\frac {\partial ^{3}w}{\partial x^{3}}}{\bigg |}_{x=L}=0\qquad {\mbox{(free end)}}\,}$

Un simple apoyo (pasador o rodillo) equivale a una fuerza puntual sobre la viga que se ajusta de tal manera que fije la posición de la viga en ese punto. Un soporte fijo o abrazadera, equivale a la combinación de una fuerza puntual y un par puntual que se ajusta de tal manera que se fije tanto la posición como la pendiente de la viga en ese punto. Las fuerzas puntuales y los momentos de torsión, ya sean de soportes o aplicados directamente, dividirán una viga en un conjunto de segmentos, entre los cuales la ecuación de la viga producirá una solución continua, dadas cuatro condiciones de contorno, dos en cada extremo del segmento. Suponiendo que el producto EI es una constante y definiendo dónde F es la magnitud de una fuerza puntual y dónde M es la magnitud de un par puntual, en la siguiente tabla se dan las condiciones de contorno apropiadas para algunos casos comunes. El cambio en una derivada particular de w a través de la frontera a medida que x aumenta se denota seguido de esa derivada. Por ejemplo, donde está el valor de en el límite inferior del segmento superior, mientras que es el valor de en el límite superior del segmento inferior. Cuando los valores de la derivada particular no sólo son continuos a lo largo de la frontera, sino que también son fijos, la condición de frontera se escribe, por ejemplo, lo que en realidad constituye dos ecuaciones separadas (por ejemplo, = fijo). ${\displaystyle \lambda =F/EI}$ ${\displaystyle \tau =M/EI}$ ${\displaystyle \Delta }$ ${\displaystyle \Delta w''=w''(x+)-w''(x-)}$ ${\displaystyle w''(x+)}$ ${\displaystyle w''}$ ${\displaystyle w''(x-)}$ ${\displaystyle w''}$ ${\displaystyle \Delta w''=0^{*}}$ ${\displaystyle w''(x-)=w''(x+)}$

Tenga en cuenta que en los primeros casos, en los que las fuerzas puntuales y los momentos de torsión se ubican entre dos segmentos, existen cuatro condiciones de contorno, dos para el segmento inferior y dos para el superior. Cuando se aplican fuerzas y momentos de torsión a un extremo de la viga, se dan dos condiciones de contorno que se aplican en ese extremo. El signo de las fuerzas puntuales y los momentos de torsión en un extremo será positivo para el extremo inferior y negativo para el extremo superior.

Consideraciones de carga

Las cargas aplicadas se pueden representar mediante condiciones de contorno o mediante la función que representa una carga distribuida externa. El uso de carga distribuida suele ser favorable por su simplicidad. Sin embargo, las condiciones de contorno se utilizan a menudo para modelar cargas según el contexto; siendo esta práctica especialmente común en el análisis de vibraciones. ${\displaystyle q(x,t)}$

Por naturaleza, la carga distribuida suele representarse por partes, ya que en la práctica una carga no suele ser una función continua. Las cargas puntuales se pueden modelar con la ayuda de la función delta de Dirac . Por ejemplo, considere una viga en voladizo uniforme estática de longitud con una carga puntual hacia arriba aplicada en el extremo libre. Utilizando condiciones de contorno, esto se puede modelar de dos maneras. En el primer enfoque, la carga puntual aplicada se aproxima mediante una fuerza cortante aplicada en el extremo libre. En ese caso, la ecuación gobernante y las condiciones de contorno son: ${\displaystyle L}$ ${\displaystyle F}$

${\displaystyle {\begin{aligned}&EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=0\\&w|_{x=0}=0\quad ;\quad {\frac {\mathrm {d} w}{\mathrm {d} x}}{\bigg |}_{x=0}=0\quad ;\quad {\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}{\bigg |}_{x=L}=0\quad ;\quad -EI{\frac {\mathrm {d} ^{3}w}{\mathrm {d} x^{3}}}{\bigg |}_{x=L}=F\,\end{aligned}}}$

Alternativamente, podemos representar la carga puntual como una distribución usando la función de Dirac. En ese caso la ecuación y las condiciones de contorno son

${\displaystyle {\begin{aligned}&EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=F\delta (x-L)\\&w|_{x=0}=0\quad ;\quad {\frac {\mathrm {d} w}{\mathrm {d} x}}{\bigg |}_{x=0}=0\quad ;\quad {\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}{\bigg |}_{x=L}=0\,\end{aligned}}}$

Tenga en cuenta que se elimina la condición de frontera de la fuerza cortante (tercera derivada); de lo contrario, habría una contradicción. Estos son problemas de valores en la frontera equivalentes y ambos producen la solución.

${\displaystyle w={\frac {F}{6EI}}(3Lx^{2}-x^{3})\,~.}$

La aplicación de varias cargas puntuales en diferentes ubicaciones conducirá a que sea una función por partes. El uso de la función Dirac simplifica enormemente estas situaciones; de lo contrario, la viga tendría que dividirse en secciones, cada una con cuatro condiciones de contorno resueltas por separado. Una familia de funciones bien organizada llamada funciones de singularidad se utiliza a menudo como abreviatura de la función de Dirac, su derivada y sus antiderivadas . ${\displaystyle w(x)}$

Los fenómenos dinámicos también se pueden modelar utilizando la ecuación de la viga estática eligiendo formas apropiadas de distribución de carga. Como ejemplo, la vibración libre de una viga se puede explicar utilizando la función de carga:

${\displaystyle q(x,t)=\mu {\frac {\partial ^{2}w}{\partial t^{2}}}\,}$

donde es la densidad de masa lineal de la viga, no necesariamente una constante. Con esta carga dependiente del tiempo, la ecuación de la viga será una ecuación diferencial parcial : ${\displaystyle \mu }$

${\displaystyle {\frac {\partial ^{2}}{\partial x^{2}}}\left(EI{\frac {\partial ^{2}w}{\partial x^{2}}}\right)=-\mu {\frac {\partial ^{2}w}{\partial t^{2}}}.}$

Otro ejemplo interesante describe la deflexión de un haz que gira con una frecuencia angular constante de : ${\displaystyle \omega }$

${\displaystyle q(x)=\mu \omega ^{2}w(x)\,}$

Esta es una distribución de fuerza centrípeta . Tenga en cuenta que, en este caso, es función del desplazamiento (la variable dependiente) y la ecuación de la viga será una ecuación diferencial ordinaria autónoma . ${\displaystyle q}$

Ejemplos

Flexión de tres puntos

La prueba de flexión en tres puntos es un experimento clásico de mecánica. Representa el caso de una viga apoyada sobre dos soportes de rodillos y sometida a una carga concentrada aplicada en el centro de la viga. El cortante es constante en valor absoluto: es la mitad de la carga central, P/2. Cambia de signo en el medio de la viga. El momento flector varía linealmente desde un extremo, donde es 0, y el centro donde su valor absoluto es PL/4, es donde el riesgo de rotura es más importante. La deformación de la viga se describe mediante un polinomio de tercer grado sobre media viga (siendo la otra mitad simétrica). Los momentos flectores ( ), fuerzas cortantes ( ) y deflexiones ( ) para una viga sometida a una carga puntual central y una carga puntual asimétrica se dan en la siguiente tabla. ^[5] ${\displaystyle M}$ ${\displaystyle Q}$ ${\displaystyle w}$

Vigas voladizas

Otra clase importante de problemas involucra vigas en voladizo . En la siguiente tabla se dan los momentos flexionantes ( ), las fuerzas cortantes ( ) y las deflexiones ( ) para una viga en voladizo sometida a una carga puntual en el extremo libre y una carga uniformemente distribuida. ^[5] ${\displaystyle M}$ ${\displaystyle Q}$ ${\displaystyle w}$

Las soluciones para varias otras configuraciones que se encuentran comúnmente están disponibles en libros de texto sobre mecánica de materiales y manuales de ingeniería.

Vigas estáticamente indeterminadas

Los momentos flectores y las fuerzas cortantes en vigas Euler-Bernoulli a menudo se pueden determinar directamente utilizando el equilibrio estático de fuerzas y momentos . Sin embargo, para ciertas condiciones de contorno, el número de reacciones puede exceder el número de ecuaciones de equilibrio independientes. ^[5] Este tipo de vigas se denominan estáticamente indeterminadas .

Las vigas incorporadas que se muestran en la siguiente figura son estáticamente indeterminadas. Para determinar las tensiones y deflexiones de dichas vigas, el método más directo es resolver la ecuación de la viga de Euler-Bernoulli con condiciones de contorno apropiadas. Pero las soluciones analíticas directas de la ecuación del haz sólo son posibles en los casos más simples. Por lo tanto, a menudo se utilizan técnicas adicionales como la superposición lineal para resolver problemas de vigas estáticamente indeterminadas.

El método de superposición implica sumar las soluciones de un número de problemas estáticamente determinados que se eligen de manera que las condiciones de contorno para la suma de los problemas individuales sumen las del problema original.

Otro problema de vigas estáticamente indeterminadas que se encuentra comúnmente es la viga en voladizo con el extremo libre apoyado sobre un rodillo. ^[5] Los momentos flectores, fuerzas cortantes y deflexiones de dicha viga se enumeran a continuación:

Extensiones

Los supuestos cinemáticos en los que se basa la teoría del haz de Euler-Bernoulli permiten ampliarla a análisis más avanzados. La superposición simple permite una carga transversal tridimensional. El uso de ecuaciones constitutivas alternativas puede permitir la deformación de la viga viscoelástica o plástica . La teoría de vigas de Euler-Bernoulli también se puede ampliar al análisis de vigas curvas, pandeo de vigas , vigas compuestas y deflexión de vigas geométricamente no lineal.

La teoría de vigas de Euler-Bernoulli no tiene en cuenta los efectos de la deformación por corte transversal . Como resultado, subestima las desviaciones y sobreestima las frecuencias naturales. Para vigas delgadas (relaciones entre longitud y espesor de la viga del orden de 20 o más), estos efectos son de menor importancia. Sin embargo, en el caso de vigas gruesas, estos efectos pueden ser significativos. Se han desarrollado teorías de haces más avanzadas, como la teoría del haz de Timoshenko (desarrollada por el científico de origen ruso Stephen Timoshenko ), para explicar estos efectos.

Grandes deflexiones

Haz de Euler-Bernoulli

La teoría original de Euler-Bernoulli es válida sólo para deformaciones infinitesimales y rotaciones pequeñas. La teoría se puede extender de manera sencilla a problemas que involucran rotaciones moderadamente grandes siempre que la deformación permanezca pequeña utilizando las deformaciones de von Kármán . ^[7]

La hipótesis de Euler-Bernoulli de que las secciones planas permanecen planas y normales al eje de la viga conducen a desplazamientos de la forma.

${\displaystyle u_{1}=u_{0}(x)-z{\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}~;~~u_{2}=0~;~~u_{3}=w_{0}(x)}$

Usando la definición de deformación de Lagrangiano de Green de la teoría de deformaciones finitas , podemos encontrar las deformaciones de von Kármán para la viga que son válidas para rotaciones grandes pero deformaciones pequeñas descartando todos los términos de orden superior (que contienen más de dos campos) excepto El las cepas resultantes toman la forma: ${\displaystyle {\frac {\partial {w}}{\partial {x^{i}}}}{\frac {\partial {w}}{\partial {x^{j}}}}.}$

${\displaystyle {\begin{aligned}\varepsilon _{11}&={\cfrac {\mathrm {d} {u_{0}}}{\mathrm {d} {x}}}-z{\cfrac {\mathrm {d} ^{2}{w_{0}}}{\mathrm {d} {x^{2}}}}+{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}-z{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\right)^{2}+\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]\approx {\cfrac {\mathrm {d} {u_{0}}}{\mathrm {d} {x}}}-z{\cfrac {\mathrm {d} ^{2}{w_{0}}}{\mathrm {d} {x^{2}}}}+{\frac {1}{2}}\left({\frac {\mathrm {d} {w_{0}}}{\mathrm {d} {x}}}\right)^{2}\\[0.25em]\varepsilon _{22}&=0\\[0.25em]\varepsilon _{33}&={\frac {1}{2}}\left({\frac {\mathrm {d} {w_{0}}}{\mathrm {d} {x}}}\right)^{2}\\[0.25em]\varepsilon _{23}&=0\\[0.25em]\varepsilon _{31}&=-{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}-z{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\right)\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)\right]\approx 0\\[0.25em]\varepsilon _{12}&=0.\end{aligned}}}$

Desde el principio del trabajo virtual , el equilibrio de fuerzas y momentos en las vigas nos da las ecuaciones de equilibrio

${\displaystyle {\begin{aligned}{\cfrac {\mathrm {d} N_{xx}}{\mathrm {d} x}}+f(x)&=0\\{\cfrac {\mathrm {d} ^{2}M_{xx}}{\mathrm {d} x^{2}}}+q(x)+{\cfrac {\mathrm {d} }{\mathrm {d} x}}\left(N_{xx}{\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)&=0\end{aligned}}}$

donde es la carga axial, es la carga transversal y ${\displaystyle f(x)}$ ${\displaystyle q(x)}$

${\displaystyle N_{xx}=\int _{A}\sigma _{xx}~\mathrm {d} A~;~~M_{xx}=\int _{A}z\sigma _{xx}~\mathrm {d} A}$

Para cerrar el sistema de ecuaciones necesitamos las ecuaciones constitutivas que relacionan tensiones con deformaciones (y por tanto tensiones con desplazamientos). Para rotaciones grandes y deformaciones pequeñas, estas relaciones son

${\displaystyle {\begin{aligned}N_{xx}&=A_{xx}\left[{\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-B_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\\M_{xx}&=B_{xx}\left[{\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-D_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\end{aligned}}}$

dónde

${\displaystyle A_{xx}=\int _{A}E~\mathrm {d} A~;~~B_{xx}=\int _{A}zE~\mathrm {d} A~;~~D_{xx}=\int _{A}z^{2}E~\mathrm {d} A~.}$

La cantidad es la rigidez a la extensión , es la rigidez a la extensión-flexión acoplada y es la rigidez a la flexión . ${\displaystyle A_{xx}}$ ${\displaystyle B_{xx}}$ ${\displaystyle D_{xx}}$

Para la situación en la que la viga tiene una sección transversal uniforme y no tiene carga axial, la ecuación rectora para una viga de Euler-Bernoulli de gran rotación es

${\displaystyle EI~{\cfrac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}-{\frac {3}{2}}~EA~\left({\cfrac {\mathrm {d} w}{\mathrm {d} x}}\right)^{2}\left({\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q(x)}$

Ver también

• Mecánica Aplicada
• Doblar
• Momento de flexión
• Pandeo
• Rigidez a la flexión
• Teoría generalizada del haz
• Teoría de placas
• Teoría del sándwich
• Diagrama de corte y momento.
• función de singularidad
• Deformación (ciencia de materiales)
• Teoría del haz de Timoshenko
• Teorema de los tres momentos (teorema de Clapeyron)
• Prueba de flexión de tres puntos

Referencias

Notas

1. Para una viga de Euler-Bernoulli que no está bajo ninguna carga axial, este eje se denomina eje neutro .

Citas

1. Timoshenko, S. (1953). Historia de la resistencia de los materiales . Nueva York: McGraw-Hill.
2. Truesdell, C. (1960). La mecánica racional de cuerpos flexibles o elásticos 1638-1788 . Venditioni Exponunt Orell Fussli Turici.
3. Ballarini, Roberto (18 de abril de 2003). "¿La teoría del haz de Da Vinci-Euler-Bernoulli?". Revista de Ingeniería Mecánica en línea . Archivado desde el original el 23 de junio de 2006 . Consultado el 22 de julio de 2006 .
4. Han, Seon M.; Benaroya, Haym; Wei, Timothy (22 de marzo de 1999). "Dinámica de vigas que vibran transversalmente utilizando cuatro teorías de ingeniería" (PDF) . Revista de Sonido y Vibración . Prensa académica. 225 (5): 935. Código bibliográfico : 1999JSV...225..935H. doi :10.1006/jsvi.1999.2257. Archivado desde el original (PDF) el 20 de julio de 2011 . Consultado el 15 de abril de 2007 .
5. Gere, JM; Timoshenko, SP (1997). Mecanica de materiales . PWS.
6. Caresta, Mauro. "Vibraciones de un haz libre" (PDF) . Consultado el 20 de marzo de 2019 .
7. Reddy, JN (2007). Análisis de elementos finitos no lineales . Prensa de la Universidad de Oxford.

Otras lecturas

• EA Witmer (1991-1992). "Teoría elemental del haz de Bernoulli-Euler". Notas del curso de ingeniería unificada del MIT . págs. 5–114 a 5–164.

enlaces externos

• Esfuerzo y deflexión de vigas, tablas de deflexión de vigas