El método de Castigliano.

Teoremas que describen materiales elásticos.

El método de Castigliano , llamado así en honor a Carlo Alberto Castigliano , es un método para determinar los desplazamientos de un sistema lineal-elástico basándose en las derivadas parciales de la energía . Es conocido por sus dos teoremas. El concepto básico puede ser fácil de entender si recordamos que un cambio de energía es igual a la fuerza causante multiplicada por el desplazamiento resultante. Por tanto, la fuerza causante es igual al cambio de energía dividido por el desplazamiento resultante. Alternativamente, el desplazamiento resultante es igual al cambio de energía dividido por la fuerza causante. Se necesitan derivadas parciales para relacionar las fuerzas causantes y los desplazamientos resultantes con el cambio de energía.

• Primer teorema de Castigliano : para fuerzas en una estructura elástica

  El método de Castigliano para calcular fuerzas es una aplicación de su primer teorema, que establece:

  Si la energía de deformación de una estructura elástica se puede expresar como una función del desplazamiento generalizado q _i entonces la derivada parcial de la energía de deformación con respecto al desplazamiento generalizado da la fuerza generalizada _Qi .

  En forma de ecuación,

  $${\displaystyle Q_{i}={\frac {\partial U}{\partial q_{i}}}}$$
  donde U es la energía de deformación. Si la curva fuerza-desplazamiento no es lineal, entonces es necesario utilizar la energía de deformación complementaria en lugar de la energía de deformación. ^[1]
• Segundo teorema de Castigliano : para desplazamientos en una estructura linealmente elástica.

  El método de Castigliano para calcular desplazamientos es una aplicación de su segundo teorema, que establece:

  Si la energía de deformación de una estructura linealmente elástica se puede expresar como una función de la fuerza generalizada Qi _entonces la derivada parcial de la energía de deformación con respecto a la fuerza generalizada da el desplazamiento generalizado q _i en la dirección de _Qi .

  Como se indicó anteriormente, esto también se puede expresar como:

  $${\displaystyle q_{i}={\frac {\partial U}{\partial Q_{i}}}.}$$

Ejemplos

Para una viga en voladizo recta y delgada con una carga P en el extremo, el desplazamiento en el extremo se puede encontrar mediante el segundo teorema de Castigliano: ${\displaystyle \delta }$

Viga en voladizo con carga puntual en el extremo libre

$${\displaystyle \delta ={\frac {\partial U}{\partial P}}}$$

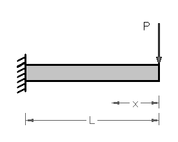
$${\displaystyle \delta ={\frac {\partial }{\partial P}}\int _{0}^{L}{{\frac {M^{2}(x)}{2EI}}dx}={\frac {\partial }{\partial P}}\int _{0}^{L}{{\frac {(Px)^{2}}{2EI}}dx}}$$

el módulo de Youngsegundo momento del área ${\displaystyle E}$ ${\displaystyle I}$ ${\displaystyle M(x)=Px}$ ${\displaystyle x}$

$${\displaystyle {\begin{aligned}\delta &=\int _{0}^{L}{{\frac {Px^{2}}{EI}}dx}\\&={\frac {PL^{3}}{3EI}}.\end{aligned}}}$$

El resultado es la fórmula estándar dada para vigas en voladizo bajo cargas finales.

enlaces externos

• carlo alberto castigliano
• El método de Castigliano: algunos ejemplos (en alemán)

Referencias

1. Historia de la resistencia de los materiales, Stephen P. Timoshenko, 1993, Dover Publications, Nueva York