En matemáticas , y más específicamente en topología algebraica y combinatoria poliédrica , la característica de Euler (o número de Euler , o característica de Euler-Poincaré ) es un invariante topológico , un número que describe la forma o estructura de un espacio topológico independientemente de la forma en que esté curvado. Se denota comúnmente por ( letra griega minúscula chi ).
La característica de Euler fue definida originalmente para poliedros y utilizada para probar varios teoremas sobre ellos, incluyendo la clasificación de los sólidos platónicos . Fue enunciada para los sólidos platónicos en 1537 en un manuscrito inédito de Francesco Maurolico . [1] Leonhard Euler , de quien se nombró el concepto, lo introdujo para poliedros convexos de manera más general, pero no logró probar rigurosamente que sea un invariante. En las matemáticas modernas, la característica de Euler surge de la homología y, de manera más abstracta, del álgebra homológica .

La característica de Euler χ se definió clásicamente para las superficies de los poliedros, según la fórmula
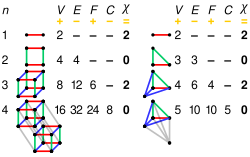
donde V , E y F son respectivamente los números de vértices (esquinas), aristas y caras del poliedro dado. La superficie de cualquier poliedro convexo tiene característica de Euler .
Esta ecuación, enunciada por Euler en 1758, [2] se conoce como fórmula del poliedro de Euler . [3] Corresponde a la característica de Euler de la esfera (es decir, ), y se aplica de forma idéntica a los poliedros esféricos . A continuación se ofrece una ilustración de la fórmula en todos los poliedros platónicos.
Las superficies de los poliedros no convexos pueden tener varias características de Euler:
Para los poliedros regulares, Arthur Cayley derivó una forma modificada de la fórmula de Euler utilizando la densidad D , la densidad de la figura del vértice y la densidad de la cara.
Todos los poliedros proyectivos tienen característica de Euler 1, como el plano proyectivo real , mientras que las superficies de los poliedros toroidales tienen característica de Euler 0, como el toro .
La característica de Euler se puede definir para gráficos planos conexos mediante la misma fórmula que para superficies poliédricas, donde F es el número de caras del gráfico, incluida la cara exterior.
La característica de Euler de cualquier grafo conexo plano G es 2. Esto se demuestra fácilmente por inducción sobre el número de caras determinado por G , comenzando con un árbol como caso base. Para árboles , y Si G tiene C componentes (grafos desconectados), el mismo argumento por inducción sobre F muestra que Uno de los pocos artículos de teoría de grafos de Cauchy también demuestra este resultado.
Mediante la proyección estereográfica, el plano se asigna a la 2-esfera, de modo que un grafo conexo se asigna a una descomposición poligonal de la esfera, que tiene característica de Euler 2. Este punto de vista está implícito en la prueba de Cauchy de la fórmula de Euler que se muestra a continuación.
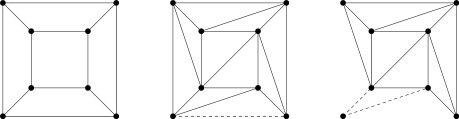
Existen numerosas demostraciones de la fórmula de Euler. Una de ellas fue dada por Cauchy en 1811, y es la siguiente: se aplica a cualquier poliedro convexo y, de manera más general, a cualquier poliedro cuyo borde sea topológicamente equivalente a una esfera y cuyas caras sean topológicamente equivalentes a discos.
Quitar una cara de la superficie poliédrica. Al separar las aristas de la cara que falta, deformar el resto en un grafo plano de puntos y curvas, de tal manera que el perímetro de la cara que falta se sitúe en el exterior, rodeando el grafo obtenido, como se ilustra en el primero de los tres grafos para el caso especial del cubo. (La suposición de que la superficie poliédrica es homeomorfa a la esfera al principio es lo que hace que esto sea posible.) Después de esta deformación, las caras regulares en general ya no son regulares. El número de vértices y aristas sigue siendo el mismo, pero el número de caras se ha reducido en 1. Por lo tanto, demostrar la fórmula de Euler para el poliedro se reduce a demostrar para este objeto plano deformado.
Si hay una cara con más de tres lados, dibuja una diagonal, es decir, una curva que pase por la cara y conecte dos vértices que aún no estén conectados. Cada nueva diagonal agrega una arista y una cara y no cambia el número de vértices, por lo que no cambia la cantidad (aquí se necesita la suposición de que todas las caras son discos para demostrar mediante el teorema de la curva de Jordan que esta operación aumenta el número de caras en uno). Continúa agregando aristas de esta manera hasta que todas las caras sean triangulares.
Aplique repetidamente cualquiera de las dos transformaciones siguientes, manteniendo invariante que el límite exterior es siempre un ciclo simple :
Estas transformaciones acaban reduciendo el gráfico planar a un único triángulo. (Sin el invariante de ciclo simple, la eliminación de un triángulo podría desconectar los triángulos restantes, invalidando el resto del argumento. Un orden de eliminación válido es un ejemplo elemental de un descascarado ).
En este punto, el triángulo solitario tiene y, por lo tanto, dado que cada uno de los dos pasos de transformación anteriores conservó esta cantidad, hemos demostrado para el objeto plano deformado, lo que demuestra para el poliedro. Esto prueba el teorema.
Para pruebas adicionales, véase Eppstein (2013). [4] Múltiples pruebas, incluyendo sus defectos y limitaciones, se utilizan como ejemplos en Proofs and Refutations de Lakatos (1976). [5]
Las superficies poliédricas analizadas anteriormente son, en lenguaje moderno, complejos CW finitos bidimensionales . (Cuando solo se utilizan caras triangulares, son complejos simpliciales finitos bidimensionales ). En general, para cualquier complejo CW finito, la característica de Euler se puede definir como la suma alternada
donde k n denota el número de celdas de dimensión n en el complejo.
De manera similar, para un complejo simplicial , la característica de Euler es igual a la suma alternada
donde k n denota el número de n -símplex en el complejo.
De manera más general, para cualquier espacio topológico , podemos definir el n- ésimo número de Betti b n como el rango del n - ésimo grupo de homología singular . La característica de Euler puede entonces definirse como la suma alternada
Esta cantidad está bien definida si los números de Betti son todos finitos y si son cero más allá de un cierto índice n 0 . Para complejos simpliciales, esta no es la misma definición que en el párrafo anterior, pero un cálculo de homología muestra que las dos definiciones darán el mismo valor para .
La característica de Euler se comporta bien con respecto a muchas operaciones básicas en espacios topológicos, como sigue.
La homología es un invariante topológico y, además, un invariante de homotopía : dos espacios topológicos que son homotópicamente equivalentes tienen grupos de homología isomorfos . De ello se deduce que la característica de Euler también es un invariante de homotopía.
Por ejemplo, cualquier espacio contráctil (es decir, una homotopía equivalente a un punto) tiene homología trivial, lo que significa que el número 0 de Betti es 1 y los otros 0. Por lo tanto, su característica de Euler es 1. Este caso incluye el espacio euclidiano de cualquier dimensión, así como la bola unitaria sólida en cualquier espacio euclidiano: el intervalo unidimensional, el disco bidimensional, la bola tridimensional, etc.
Por poner otro ejemplo, cualquier poliedro convexo es homeomorfo a la bola tridimensional , por lo que su superficie es homeomorfa (y por tanto homotópicamente equivalente) a la esfera bidimensional , que tiene característica de Euler 2. Esto explica por qué la superficie de un poliedro convexo tiene característica de Euler 2.
Si M y N son dos espacios topológicos cualesquiera, entonces la característica de Euler de su unión disjunta es la suma de sus características de Euler, ya que la homología es aditiva bajo la unión disjunta:
En términos más generales, si M y N son subespacios de un espacio mayor X , entonces también lo son su unión e intersección. En algunos casos, la característica de Euler obedece a una versión del principio de inclusión-exclusión :
Esto es cierto en los siguientes casos:
En general, el principio de inclusión-exclusión es falso. Se da un contraejemplo tomando X como la recta real , M como un subconjunto formado por un punto y N como el complemento de M.
Para dos variedades n cerradas y conexas se puede obtener una nueva variedad conexa mediante la operación de suma conexa . La característica de Euler está relacionada con la fórmula [8]
Además, la característica de Euler de cualquier espacio de producto M × N es
Estas propiedades de adición y multiplicación también se disfrutan en la cardinalidad de los conjuntos . De esta manera, la característica de Euler puede considerarse como una generalización de la cardinalidad; véase [1].
De manera similar, para un espacio de recubrimiento con láminas k, se tiene
De manera más general, para un espacio de cobertura ramificado , la característica de Euler de la cobertura se puede calcular a partir de lo anterior, con un factor de corrección para los puntos de ramificación, lo que produce la fórmula de Riemann-Hurwitz .
La propiedad del producto se cumple de manera mucho más general, para fibraciones con ciertas condiciones.
Si es una fibración con fibra F, con la base B conexa por caminos , y la fibración es orientable sobre un campo K, entonces la característica de Euler con coeficientes en el campo K satisface la propiedad del producto: [9]
Esto incluye espacios de productos y espacios de cobertura como casos especiales, y puede demostrarse mediante la secuencia espectral de Serre sobre la homología de una fibración.
Para los haces de fibras, esto también se puede entender en términos de un mapa de transferencia (nótese que esto es una elevación y va "en la dirección equivocada") cuya composición con el mapa de proyección es la multiplicación por la clase de Euler de la fibra: [10]
La característica de Euler se puede calcular fácilmente para superficies generales encontrando una poligonización de la superficie (es decir, una descripción como un complejo CW ) y utilizando las definiciones anteriores.
Es habitual construir balones de fútbol uniendo piezas pentagonales y hexagonales, con tres piezas unidas en cada vértice (véase, por ejemplo, el Adidas Telstar ). Si se utilizan P pentágonos y H hexágonos, entonces hay caras, vértices y aristas. La característica de Euler es, por tanto:
Como la esfera tiene característica de Euler 2, se deduce que Es decir, un balón de fútbol construido de esta manera siempre tiene 12 pentágonos. El número de hexágonos puede ser cualquier entero no negativo excepto 1. [11] Este resultado es aplicable a los fulerenos y a los poliedros de Goldberg .
La esfera n- dimensional tiene grupos de homología singulares iguales a
por lo tanto tiene número de Betti 1 en dimensiones 0 y n , y todos los demás números de Betti son 0. Su característica de Euler es entonces χ = 1 + (−1) n ; es decir, 0 si n es impar , o 2 si n es par .
El espacio proyectivo real de dimensión n es el cociente de la esfera n por la función antípoda . De ello se deduce que su característica de Euler es exactamente la mitad de la de la esfera correspondiente, es decir, 0 o 1.
El toro de dimensión n es el espacio producto de n círculos. Su característica de Euler es 0, por la propiedad del producto. En términos más generales, cualquier variedad compacta paralelizable , incluido cualquier grupo de Lie compacto , tiene una característica de Euler 0. [12]
La característica de Euler de cualquier variedad cerrada de dimensión impar es también 0. [13] El caso de los ejemplos orientables es un corolario de la dualidad de Poincaré . Esta propiedad se aplica de manera más general a cualquier espacio estratificado compacto cuyos estratos tengan todos dimensión impar. También se aplica a variedades cerradas de dimensión impar no orientables, a través de la doble cubierta orientable dos a uno .
La característica de Euler de una superficie orientable cerrada se puede calcular a partir de su género g (el número de toros en una descomposición de suma conectada de la superficie; intuitivamente, el número de "asas") como
La característica de Euler de una superficie cerrada no orientable se puede calcular a partir de su género no orientable k (el número de planos proyectivos reales en una descomposición de suma conexa de la superficie) como
Para variedades cerradas y lisas, la característica de Euler coincide con el número de Euler , es decir, la clase de Euler de su fibrado tangente evaluada sobre la clase fundamental de una variedad. La clase de Euler, a su vez, se relaciona con todas las demás clases características de fibrados vectoriales .
Para variedades de Riemann cerradas , la característica de Euler también se puede encontrar integrando la curvatura; véase el teorema de Gauss-Bonnet para el caso bidimensional y el teorema de Gauss-Bonnet generalizado para el caso general.
Un análogo discreto del teorema de Gauss-Bonnet es el teorema de Descartes , que sostiene que el " defecto total " de un poliedro , medido en círculos completos, es la característica de Euler del poliedro.
El teorema de Hadwiger caracteriza la característica de Euler como la única función de conjunto invariante en cuanto a traducción, finitamente aditiva y no necesariamente no negativa ( hasta la multiplicación escalar ) definida en uniones finitas de conjuntos convexos compactos en ℝ n que es "homogénea de grado 0".
Para cada complejo combinatorio de celdas , se define la característica de Euler como el número de celdas 0, menos el número de celdas 1, más el número de celdas 2, etc., si esta suma alternada es finita. En particular, la característica de Euler de un conjunto finito es simplemente su cardinalidad, y la característica de Euler de un grafo es el número de vértices menos el número de aristas. (Olaf Post llama a esto una "fórmula bien conocida". [14] )
De manera más general, se puede definir la característica de Euler de cualquier complejo de cadena como la suma alternada de los rangos de los grupos de homología del complejo de cadena, asumiendo que todos estos rangos son finitos. [15]
Una versión de la característica de Euler utilizada en geometría algebraica es la siguiente. Para cualquier haz coherente en un esquema propio X , se define su característica de Euler como
donde es la dimensión del i - ésimo grupo de cohomología de haces de . En este caso, las dimensiones son todas finitas según el teorema de finitud de Grothendieck . Este es un ejemplo de la característica de Euler de un complejo de cadena, donde el complejo de cadena es una resolución finita de mediante haces acíclicos.
Otra generalización del concepto de característica de Euler en variedades proviene de los orbifolds (ver Característica de Euler de un orbifold ). Si bien cada variedad tiene una característica de Euler entera, un orbifold puede tener una característica de Euler fraccionaria. Por ejemplo, el orbifold en forma de lágrima tiene característica de Euler 1 + 1/ pag , donde p es un número primo correspondiente al ángulo del cono 2π / pag .
El concepto de característica de Euler de la homología reducida de un conjunto parcial finito acotado es otra generalización, importante en combinatoria . Un conjunto parcial está "acotado" si tiene elementos más pequeños y más grandes; llamémoslos 0 y 1. La característica de Euler de un conjunto parcial de este tipo se define como el entero μ (0,1) , donde μ es la función de Möbius en el álgebra de incidencia de ese conjunto parcial .
Esto se puede generalizar aún más definiendo una característica de Euler de valor racional para ciertas categorías finitas , una noción compatible con las características de Euler de grafos, orbifolds y posets mencionados anteriormente. En este contexto, la característica de Euler de un grupo finito o monoide G es 1/ | Sol | , y la característica de Euler de un grupoide finito es la suma de 1/ | Sol | , donde elegimos un grupo representativo G i para cada componente conectado del grupoide. [16]