La teoría de la gravitación de Le Sage es una teoría cinética de la gravedad propuesta originalmente por Nicolas Fatio de Duillier en 1690 y posteriormente por Georges-Louis Le Sage en 1748. La teoría proponía una explicación mecánica de la fuerza gravitatoria de Newton en términos de corrientes de diminutas partículas invisibles (a las que Le Sage llamó corpúsculos ultramundanos) que impactaban contra todos los objetos materiales desde todas las direcciones. Según este modelo, dos cuerpos materiales cualesquiera se protegen parcialmente mutuamente de los corpúsculos que chocan, lo que da como resultado un desequilibrio neto en la presión ejercida por el impacto de los corpúsculos sobre los cuerpos, que tiende a empujarlos entre sí. Esta explicación mecánica de la gravedad nunca obtuvo una aceptación generalizada.

La teoría postula que la fuerza de gravedad es el resultado de partículas diminutas (corpúsculos) que se mueven a gran velocidad en todas direcciones, a lo largo del universo . Se supone que la intensidad del flujo de partículas es la misma en todas las direcciones, por lo que un objeto aislado A es golpeado por igual desde todos los lados, lo que resulta solo en una presión dirigida hacia adentro , pero no en una fuerza direccional neta (P1).
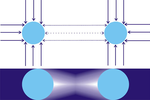
Sin embargo, si hay un segundo objeto B presente, una fracción de las partículas que de otro modo habrían golpeado a A desde la dirección de B es interceptada, por lo que B funciona como un escudo, es decir, desde la dirección de B, A será golpeado por menos partículas que desde la dirección opuesta. Del mismo modo, B será golpeado por menos partículas desde la dirección de A que desde la dirección opuesta. Se puede decir que A y B se "hacen sombra" mutuamente, y los dos cuerpos son empujados uno hacia el otro por el desequilibrio de fuerzas resultante (P2). Por lo tanto, la atracción aparente entre cuerpos es, según esta teoría, en realidad un empuje disminuido desde la dirección de otros cuerpos, por lo que la teoría a veces se llama gravedad de empuje o gravedad de sombra , aunque se la conoce más ampliamente como gravedad de Lesage .

Si las colisiones del cuerpo A y las partículas gravitacionales son completamente elásticas , la intensidad de las partículas reflejadas sería tan fuerte como la de las entrantes, por lo que no surgiría ninguna fuerza direccional neta. Lo mismo es cierto si se introduce un segundo cuerpo B, donde B actúa como un escudo contra las partículas gravitacionales en la dirección de A. La partícula gravitacional C que ordinariamente chocaría contra A es bloqueada por B, pero otra partícula D que ordinariamente no habría chocado con A, es redirigida por la reflexión en B y, por lo tanto, reemplaza a C. Por lo tanto, si las colisiones son completamente elásticas, las partículas reflejadas entre A y B compensarían completamente cualquier efecto de sombra. Para tener en cuenta una fuerza gravitacional neta, debe suponerse que las colisiones no son completamente elásticas, o al menos que las partículas reflejadas se desaceleran, de modo que su momento se reduce después del impacto. Esto daría como resultado corrientes con un momento disminuido que parten de A y corrientes con un momento no disminuido que llegan a A, por lo que surgiría un momento direccional neto hacia el centro de A (P3). Bajo este supuesto, las partículas reflejadas en el caso de dos cuerpos no compensarán completamente el efecto de sombra, porque el flujo reflejado es más débil que el flujo incidente.

Dado que se supone que algunas o todas las partículas gravitatorias que convergen sobre un objeto son absorbidas o ralentizadas por éste, se deduce que la intensidad del flujo de partículas gravitatorias que emana de la dirección de un objeto masivo es menor que el flujo que converge sobre el objeto. Podemos imaginar este desequilibrio del flujo de momento –y, por lo tanto, de la fuerza ejercida sobre cualquier otro cuerpo en las proximidades– distribuido sobre una superficie esférica centrada en el objeto (P4). El desequilibrio del flujo de momento sobre una superficie esférica completa que encierra al objeto es independiente del tamaño de la esfera que la encierra, mientras que el área de la superficie de la esfera aumenta en proporción al cuadrado del radio. Por lo tanto, el desequilibrio del momento por unidad de área disminuye inversamente al cuadrado de la distancia.
De las premisas expuestas hasta ahora, sólo se desprende una fuerza proporcional a la superficie de los cuerpos. Pero la gravedad es proporcional a las masas. Para satisfacer la necesidad de proporcionalidad de la masa, la teoría postula que a) los elementos básicos de la materia son muy pequeños, de modo que la materia bruta consiste principalmente en espacio vacío, y b) que las partículas son tan pequeñas que sólo una pequeña fracción de ellas sería interceptada por la materia bruta. El resultado es que la "sombra" de cada cuerpo es proporcional a la superficie de cada elemento individual de la materia. Si se supone entonces que los elementos opacos elementales de toda la materia son idénticos (es decir, que tienen la misma relación entre densidad y área), se deducirá que el efecto de sombra es, al menos aproximadamente, proporcional a la masa (P5).

Nicolas Fatio presentó la primera formulación de sus ideas sobre la gravitación en una carta a Christiaan Huygens en la primavera de 1690. [1] Dos días después, Fatio leyó el contenido de la carta ante la Royal Society en Londres. En los años siguientes, Fatio compuso varios borradores manuscritos de su obra principal De la Cause de la Pesanteur , pero ninguno de este material fue publicado durante su vida. En 1731, Fatio también envió su teoría como un poema en latín, al estilo de Lucrecio , a la Academia de Ciencias de París, pero fue rechazado. Algunos fragmentos de estos manuscritos y copias del poema fueron adquiridos más tarde por Le Sage , quien no logró encontrar un editor para los artículos de Fatio. [2] Así duró hasta 1929, [3] cuando Karl Bopp publicó la única copia completa del manuscrito de Fatio , y en 1949 [4] Gagnebin utilizó los fragmentos recopilados en posesión de Le Sage para reconstruir el artículo. La edición de Gagnebin incluye revisiones realizadas por Fatio hasta 1743, cuarenta años después de que compusiera el borrador en el que se basó la edición de Bopp. Sin embargo, la segunda mitad de la edición de Bopp contiene las partes matemáticamente más avanzadas de la teoría de Fatio, y no fueron incluidas por Gagnebin en su edición. Para un análisis detallado del trabajo de Fatio y una comparación entre las ediciones de Bopp y de Gagnebin, véase Zehe [5] La siguiente descripción se basa principalmente en la edición de Bopp.

Fatio supuso que el universo está lleno de partículas diminutas que se mueven indiscriminadamente a gran velocidad y de forma rectilínea en todas direcciones. Para ilustrar sus ideas utilizó el siguiente ejemplo: supongamos un objeto C , sobre el que se dibuja un pequeño plano infinito zz y una esfera centrada en zz . En esta esfera Fatio colocó la pirámide PzzQ , en la que fluyen algunas partículas en la dirección de zz y también algunas partículas, que ya fueron reflejadas por C y, por lo tanto, se alejan de zz . Fatio propuso que la velocidad media de las partículas reflejadas es menor y, por lo tanto, su momento es menor que el de las partículas incidentes. El resultado es una corriente , que empuja a todos los cuerpos en la dirección de zz . Así, por un lado, la velocidad de la corriente permanece constante, pero por otro lado, a mayor proximidad a zz, la densidad de la corriente aumenta y, por lo tanto, su intensidad es proporcional a 1/ r 2 . Y como se puede dibujar un número infinito de tales pirámides alrededor de C , la proporcionalidad se aplica a todo el rango alrededor de C .
Para justificar la suposición de que las partículas viajan después de su reflexión con velocidades disminuidas, Fatio enunció las siguientes suposiciones:
Estos pasajes son las partes más incomprensibles de la teoría de Fatio, porque nunca decidió claramente qué tipo de colisión prefería en realidad. Sin embargo, en la última versión de su teoría en 1742 acortó los pasajes relacionados y atribuyó "elasticidad perfecta o fuerza de resorte" a las partículas y, por otro lado, "elasticidad imperfecta" a la materia bruta, por lo que las partículas se reflejarían con velocidades reducidas. Además, Fatio se enfrentó a otro problema: ¿qué sucede si las partículas chocan entre sí? Las colisiones inelásticas conducirían a una disminución constante de la velocidad de las partículas y, por lo tanto, a una disminución de la fuerza gravitatoria. Para evitar este problema, Fatio supuso que el diámetro de las partículas es muy pequeño en comparación con su distancia mutua, por lo que sus interacciones son muy raras.
Fatio pensó durante mucho tiempo que, puesto que los corpúsculos se aproximan a los cuerpos materiales a una velocidad mayor que la que se alejan de ellos (después de la reflexión), habría una acumulación progresiva de corpúsculos cerca de los cuerpos materiales (un efecto que él llamó "condensación"). Sin embargo, más tarde se dio cuenta de que, aunque los corpúsculos entrantes son más rápidos, están más espaciados que los corpúsculos reflejados, por lo que las velocidades de flujo de entrada y salida son las mismas. Por lo tanto, no hay acumulación secular de corpúsculos, es decir, la densidad de los corpúsculos reflejados permanece constante (suponiendo que sean lo suficientemente pequeños como para que no se produzca una tasa notablemente mayor de autocolisión cerca del cuerpo masivo). Más importante aún, Fatio observó que, al aumentar tanto la velocidad como la elasticidad de los corpúsculos, la diferencia entre las velocidades de los corpúsculos entrantes y reflejados (y, por lo tanto, la diferencia en densidades) puede hacerse arbitrariamente pequeña mientras se mantiene la misma fuerza gravitatoria efectiva.

Para garantizar la proporcionalidad de la masa, Fatio supuso que la materia bruta es extremadamente permeable al flujo de corpúsculos. Esbozó tres modelos para justificar esta suposición:
En 1690 Fatio supuso que la "fuerza de empuje" ejercida por las partículas sobre una superficie plana es la sexta parte de la fuerza que se produciría si todas las partículas estuvieran alineadas perpendicularmente a la superficie. Fatio demostró esta proposición determinando la fuerza que ejercen las partículas sobre un punto determinado zz. Derivó la fórmula p = ρv 2 zz /6. Esta solución es muy similar a la fórmula conocida en la teoría cinética de los gases p = ρv 2 /3, que fue encontrada por Daniel Bernoulli en 1738. Esta fue la primera vez que se señaló una solución análoga al resultado similar en la teoría cinética , mucho antes de que se desarrollara el concepto básico de esta última teoría. Sin embargo, el valor de Bernoulli es el doble del de Fatio, porque según Zehe, Fatio solo calculó el valor mv para el cambio de impulso después de la colisión, pero no 2 mv y, por lo tanto, obtuvo un resultado erróneo. (Su resultado sólo es correcto en el caso de colisiones totalmente inelásticas.) Fatio intentó utilizar su solución no sólo para explicar la gravitación, sino también para explicar el comportamiento de los gases. Trató de construir un termómetro que indicase el "estado de movimiento" de las moléculas del aire y, por tanto, estimase la temperatura. Pero Fatio (a diferencia de Bernoulli) no identificó el calor y los movimientos de las partículas del aire, sino que utilizó otro fluido que debería ser el responsable de este efecto. Tampoco se sabe si Bernoulli estuvo influido por Fatio o no.
En este capítulo, Fatio examina las conexiones entre el término infinito y sus relaciones con su teoría. Fatio a menudo justificaba sus consideraciones con el hecho de que diferentes fenómenos son "infinitamente más pequeños o más grandes" que otros y, por lo tanto, muchos problemas pueden reducirse a un valor indetectable. Por ejemplo, el diámetro de las barras es infinitamente más pequeño que la distancia entre ellas; o la velocidad de las partículas es infinitamente mayor que la de la materia bruta; o la diferencia de velocidad entre partículas reflejadas y no reflejadas es infinitamente pequeña.
Esta es la parte matemáticamente más compleja de la teoría de Fatio. Allí trató de estimar la resistencia de las corrientes de partículas a los cuerpos en movimiento. Suponiendo que u es la velocidad de la materia bruta, v es la velocidad de las partículas gravitatorias y ρ la densidad del medio. En el caso v ≪ u y ρ = constante Fatio afirmó que la resistencia es ρu 2 . En el caso v ≫ u y ρ = constante la resistencia es 4/3 ρuv . Ahora bien, Newton afirmó que la falta de resistencia al movimiento orbital requiere una escasez extrema de cualquier medio en el espacio. Así que Fatio disminuyó la densidad del medio y afirmó que, para mantener una fuerza gravitatoria suficiente, esta reducción debe compensarse cambiando v " inversamente proporcional a la raíz cuadrada de la densidad ". Esto se deduce de la presión de partículas de Fatio, que es proporcional a ρv 2 . Según Zehe, el intento de Fatio de aumentar v a un valor muy alto en realidad dejaría la resistencia muy pequeña en comparación con la gravedad, porque la resistencia en el modelo de Fatio es proporcional a ρuv pero la gravedad (es decir, la presión de la partícula) es proporcional a ρv 2 .
Fatio estuvo en comunicación con algunos de los científicos más famosos de su tiempo.

Entre 1690 y 1693, Isaac Newton y Fatio mantuvieron una estrecha relación personal . Las afirmaciones de Newton sobre la teoría de Fatio diferían ampliamente. Por ejemplo, después de describir las condiciones necesarias para una explicación mecánica de la gravedad, escribió en una nota (inédita) en su propia copia impresa de los Principia en 1692: La única hipótesis por la que se puede explicar la gravedad es, sin embargo, de este tipo, y fue ideada por primera vez por el ingeniosísimo geómetra Sr. N. Fatio. [5] Por otra parte, el propio Fatio afirmó que, aunque Newton había comentado en privado que la teoría de Fatio era la mejor explicación mecánica posible de la gravedad, también reconoció que Newton tendía a creer que la verdadera explicación de la gravitación no era mecánica. Gregory también anotó en sus "Memorandas": " El señor Newton y el señor Halley se ríen de la manera en que el señor Fatio explica la gravedad " . [5] Supuestamente él anotó esto el 28 de diciembre de 1691. Sin embargo, se desconoce la fecha real, porque tanto la tinta como la pluma que se utilizaron difieren del resto de la página. Después de 1694, la relación entre los dos hombres se enfrió.
Christiaan Huygens fue la primera persona a la que Fatio informó de su teoría, pero nunca la aceptó. Fatio creía haber convencido a Huygens de la consistencia de su teoría, pero Huygens lo negó en una carta a Gottfried Leibniz . También hubo una breve correspondencia entre Fatio y Leibniz sobre la teoría. Leibniz criticó la teoría de Fatio por exigir un espacio vacío entre las partículas, lo que él (Leibniz) rechazó por motivos filosóficos. Jakob Bernoulli expresó su interés en la teoría de Fatio y le instó a escribir sus pensamientos sobre la gravitación en un manuscrito completo, lo que realmente hizo Fatio. Bernoulli luego copió el manuscrito, que ahora se encuentra en la biblioteca universitaria de Basilea y fue la base de la edición de Bopp.
Sin embargo, la teoría de Fatio permaneció en gran parte desconocida con algunas excepciones como Cramer y Le Sage, porque nunca pudo publicar formalmente sus obras y cayó bajo la influencia de un grupo de fanáticos religiosos llamados los "profetas franceses" (que pertenecían a los camisards ) y por lo tanto su reputación pública quedó arruinada.
En 1731, el matemático suizo Gabriel Cramer publicó una disertación, [6] al final de la cual aparecía un esbozo de una teoría muy similar a la de Fatio –incluyendo la estructura neta de la materia, analogía con la luz, sombreado– pero sin mencionar el nombre de Fatio. Fatio sabía que Cramer tenía acceso a una copia de su artículo principal, por lo que acusó a Cramer de solo repetir su teoría sin comprenderla. También fue Cramer quien informó a Le Sage sobre la teoría de Fatio en 1749. En 1736, el médico alemán Franz Albert Redeker también publicó una teoría similar. [7] Se desconoce cualquier conexión entre Redeker y Fatio.

La primera exposición de su teoría, Essai sur l'origine des force mortes , fue enviada por Le Sage a la Academia de Ciencias de París en 1748, pero nunca fue publicada. [2] Según Le Sage, después de crear y enviar su ensayo , se informó sobre las teorías de Fatio, Cramer y Redeker. En 1756, por primera vez, se publicó una de sus exposiciones de la teoría, [8] y en 1758 envió una exposición más detallada, Essai de Chymie Méchanique , a un concurso en la Academia de Ciencias de Rouen . [9] En este artículo, intentó explicar tanto la naturaleza de la gravitación como las afinidades químicas. La exposición de la teoría que se hizo accesible a un público más amplio, Lucrèce Newtonien (1784), en la que se desarrolló plenamente la correspondencia con los conceptos de Lucrecio. [10] Otra exposición de la teoría fue publicada póstumamente por Pierre Prévost en 1818 a partir de las notas de Le Sage. [11]

Le Sage discutió la teoría en gran detalle y propuso estimaciones cuantitativas para algunos de los parámetros de la teoría.
Le Sage afirmó que él fue el primero en sacar todas las consecuencias de la teoría y también Prévost afirmó que la teoría de Le Sage estaba más desarrollada que la de Fatio. [2] Sin embargo, al comparar las dos teorías y después de un análisis detallado de los documentos de Fatio (que también estaban en posesión de Le Sage), Zehe juzgó que Le Sage no aportaba nada esencialmente nuevo y que a menudo no alcanzaba el nivel de Fatio. [5]
Las ideas de Le Sage no fueron bien recibidas en su época, excepto por algunos de sus amigos y asociados como Pierre Prévost , Charles Bonnet , Jean-André Deluc , Charles Mahon, tercer conde Stanhope y Simon L'Huillier . Mencionaron y describieron la teoría de Le Sage en sus libros y artículos, que fueron utilizados por sus contemporáneos como fuente secundaria para la teoría de Le Sage (debido a la falta de artículos publicados por el propio Le Sage).
Leonhard Euler comentó en cierta ocasión que el modelo de Le Sage era "infinitamente mejor" que el de todos los demás autores y que todas las objeciones se compensaban en este modelo, pero más tarde dijo que la analogía con la luz no tenía peso para él, porque creía en la naturaleza ondulatoria de la luz. Después de pensarlo más, Euler llegó a desaprobar el modelo y le escribió a Le Sage: [12]
Debe usted disculparme, señor, si siento una gran repugnancia por sus corpúsculos ultramundanos, y preferiré siempre confesar mi ignorancia de la causa de la gravedad que recurrir a hipótesis tan extrañas.
Daniel Bernoulli se mostró satisfecho con la similitud entre el modelo de Le Sage y sus propias ideas sobre la naturaleza de los gases. Sin embargo, el propio Bernoulli opinaba que su propia teoría cinética de los gases era sólo una especulación y, asimismo, consideraba que la teoría de Le Sage era altamente especulativa. [13]
Roger Joseph Boscovich señaló que la teoría de Le Sage es la primera que realmente puede explicar la gravedad por medios mecánicos. Sin embargo, rechazó el modelo debido a la enorme cantidad de materia ultramundana sin utilizar. John Playfair describió los argumentos de Boscovich diciendo:
Una inmensa multitud de átomos, destinados así a proseguir su viaje sin fin a través del infinito del espacio, sin cambiar de dirección ni volver al lugar de donde vinieron, es una suposición muy poco admitida por la economía habitual de la naturaleza. ¿De dónde proviene el suministro de estos innumerables torrentes? ¿No debe implicar un ejercicio perpetuo de poder creador, infinito tanto en extensión como en duración? [14]
Un argumento muy similar fue presentado posteriormente por Maxwell (ver las secciones siguientes). Además, Boscovich negó la existencia de todo contacto e impulso inmediato, pero propuso acciones repulsivas y atractivas a distancia .
El conocimiento que Georg Christoph Lichtenberg tenía de la teoría de Le Sage [15] se basaba en “Lucrece Newtonien” y en un resumen de Prévost. Lichtenberg creía originalmente (como Descartes) que toda explicación de los fenómenos naturales debía basarse en el movimiento rectilíneo y la impulsión, y la teoría de Le Sage cumplía estas condiciones. En 1790 expresó en uno de sus artículos su entusiasmo por la teoría, creyendo que la teoría de Le Sage abarcaba todo nuestro conocimiento y hacía inútil cualquier otro sueño sobre ese tema. Continuó diciendo: “Si es un sueño, es el más grande y el más magnífico que jamás se haya soñado…” y que podemos llenar con él un vacío en nuestros libros, que sólo puede ser llenado por un sueño. [16]
Lichtenberg se refirió a menudo a la teoría de Le Sage en sus conferencias sobre física en la Universidad de Göttingen . Sin embargo, alrededor de 1796 Lichtenberg cambió sus puntos de vista después de ser persuadido por los argumentos de Immanuel Kant , quien criticó cualquier tipo de teoría que intentara reemplazar la atracción por la impulsión. [17] Kant señaló que la existencia misma de configuraciones de materia extendidas espacialmente, como partículas de radio distinto de cero, implica la existencia de algún tipo de fuerza vinculante para mantener unidas las partes extendidas de la partícula. Ahora bien, esa fuerza no puede explicarse por el empuje de las partículas gravitacionales, porque esas partículas también deben mantenerse unidas de la misma manera. Para evitar este razonamiento circular , Kant afirmó que debe existir una fuerza de atracción fundamental. Esta era precisamente la misma objeción que siempre se había planteado contra la doctrina del impulso de Descartes en el siglo anterior, y que había llevado incluso a los seguidores de Descartes a abandonar ese aspecto de su filosofía.
Otro filósofo alemán, Friedrich Wilhelm Joseph Schelling , rechazó el modelo de Le Sage porque su materialismo mecanicista era incompatible con la filosofía muy idealista y antimaterialista de Schelling. [18]
En parte, teniendo en cuenta la teoría de Le Sage, Pierre-Simon Laplace se propuso determinar la velocidad necesaria de la gravedad para que fuera coherente con las observaciones astronómicas. Calculó que la velocidad debía ser “al menos cien millones de veces mayor que la de la luz”, para evitar desigualdades inaceptablemente grandes debidas a efectos de aberración en el movimiento lunar. [19] La mayoría de los investigadores, incluido Laplace, tomaron esto como respaldo al concepto newtoniano de acción instantánea a distancia y como indicación de la improbabilidad de cualquier modelo como el de Le Sage. Laplace también argumentó que, para mantener la proporcionalidad de la masa, el límite superior de la superficie molecular de la Tierra es, como máximo, la diezmillonésima parte de la superficie terrestre. Para decepción de Le Sage, Laplace nunca mencionó directamente la teoría de Le Sage en sus obras.
Como las teorías de Fatio, Cramer y Redeker no eran ampliamente conocidas, la exposición de la teoría por parte de Le Sage gozó de un resurgimiento de interés en la segunda mitad del siglo XIX, coincidiendo con el desarrollo de la teoría cinética de los gases .
Como las partículas de Le Sage deben perder velocidad al chocar con la materia ordinaria (para producir una fuerza gravitatoria neta), una enorme cantidad de energía debe convertirse en modos de energía internos. Si esas partículas no tienen modos de energía internos, el exceso de energía solo puede ser absorbido por la materia ordinaria. Para abordar este problema, Armand Jean Leray [20] propuso un modelo de partículas (perfectamente similar al de Le Sage) en el que afirmaba que la energía absorbida es utilizada por los cuerpos para producir magnetismo y calor . Sugirió que esto podría ser una respuesta a la pregunta de dónde proviene la energía de salida de las estrellas.

La teoría de Le Sage se convirtió en un tema de renovado interés en la última parte del siglo XIX, tras un artículo publicado por Kelvin en 1873. [21] A diferencia de Leray, que trató el problema del calor de forma imprecisa, Kelvin afirmó que la energía absorbida representa un calor muy alto, suficiente para vaporizar cualquier objeto en una fracción de segundo. De modo que Kelvin reiteró una idea que Fatio había propuesto originalmente en la década de 1690 para intentar abordar el problema termodinámico inherente a la teoría de Le Sage. Propuso que el exceso de calor podría ser absorbido por los modos de energía internos de las propias partículas, basándose en su propuesta de la naturaleza de vórtice de la materia. En otras palabras, la energía cinética traslacional original de las partículas se transfiere a los modos de energía internos, principalmente vibracionales o rotacionales, de las partículas. Apelando a la proposición de Clausius de que la energía en cualquier modo particular de una molécula de gas tiende hacia una proporción fija de la energía total, Kelvin continuó sugiriendo que las partículas energizadas pero de movimiento más lento serían restauradas posteriormente a su condición original debido a colisiones (a escala cosmológica) con otras partículas. Kelvin también afirmó que sería posible extraer cantidades ilimitadas de energía libre del flujo ultramundano, y describió una máquina de movimiento perpetuo para lograrlo.
Posteriormente, Peter Guthrie Tait afirmó que la teoría de Le Sage era la única explicación plausible de la gravitación que se había propuesto hasta ese momento. Continuó diciendo:
Lo más singular de esto es que, si fuera cierto, probablemente nos llevaría a considerar todo tipo de energía como en última instancia cinética. [22]
Sin embargo, el propio Kelvin no era optimista en cuanto a que la teoría de Le Sage pudiera dar una explicación satisfactoria de los fenómenos. Después de su breve artículo de 1873, mencionado anteriormente, nunca volvió a tratar el tema, excepto para hacer el siguiente comentario:
Esta teoría cinética de la materia es un sueño, y no puede ser otra cosa hasta que pueda explicar la afinidad química, la electricidad, el magnetismo, la gravitación y la inercia de las masas (es decir, las multitudes) de los vórtices. La teoría de Le Sage podría dar una explicación de la gravedad y de su relación con la inercia de las masas, según la teoría de los vórtices, si no fuera por la eolotropía esencial de los cristales y la isotropía aparentemente perfecta de la gravedad. No se ha descubierto, ni se ha imaginado que se pueda descubrir, ningún indicio que indique un camino que pueda llevar a superar esta dificultad o a hacerla girar en torno a ella. [23]
Samuel Tolver Preston [24] ilustró que muchos de los postulados introducidos por Le Sage sobre las partículas gravitacionales, como el movimiento rectilíneo, las interacciones raras, etc. , podían agruparse bajo la noción única de que se comportaban (a escala cosmológica) como las partículas de un gas con un camino libre medio extremadamente largo . Preston también aceptó la propuesta de Kelvin de los modos de energía interna de las partículas. Ilustró el modelo de Kelvin comparándolo con la colisión de un anillo de acero y un yunque: el yunque no se sacudiría mucho, pero el anillo de acero estaría en un estado de vibración y, por lo tanto, se aleja con velocidad disminuida. También argumentó que el camino libre medio de las partículas es al menos la distancia entre los planetas: en distancias más largas, las partículas recuperan su energía de traslación debido a las colisiones entre sí, por lo que concluyó que en distancias más largas no habría atracción entre los cuerpos, independientemente de su tamaño . Paul Drude sugirió que esto podría ser una conexión con algunas teorías de Carl Gottfried Neumann y Hugo von Seeliger , quienes propusieron algún tipo de absorción de la gravedad en el espacio abierto. [25]

James Clerk Maxwell publicó una revisión de la teoría de Kelvin-Le Sage en la novena edición de la Encyclopædia Britannica bajo el título Atom en 1875. [26] Después de describir el concepto básico de la teoría, escribió (con sarcasmo según Aronson): [27]
He aquí, pues, un camino que conduce a una explicación de la ley de la gravitación, que, si se puede demostrar que es en otros aspectos consistente con los hechos, puede resultar un camino real hacia los mismos arcanos de la ciencia. [26]
Maxwell comentó sobre la sugerencia de Kelvin de diferentes modos de energía de las partículas que esto implica que las partículas gravitacionales no son entidades primitivas simples, sino más bien sistemas, con sus propios modos de energía internos, que deben mantenerse unidos por fuerzas de atracción (inexplicadas). Sostiene que la temperatura de los cuerpos debe tender a acercarse a aquella en la que la energía cinética promedio de una molécula del cuerpo sería igual a la energía cinética promedio de una partícula ultramundana y afirma que la última cantidad debe ser mucho mayor que la primera y concluye que la materia ordinaria debería incinerarse en cuestión de segundos bajo el bombardeo de Le Sage. [26] Escribió:
Hemos dedicado a esta teoría más espacio del que parece merecer, porque es ingeniosa y porque es la única teoría de la causa de la gravitación que ha sido desarrollada hasta el momento como para ser susceptible de ser atacada y defendida. [26]
Maxwell también argumentó que la teoría requiere "un enorme gasto de energía externa" y, por lo tanto, viola la conservación de la energía como principio fundamental de la naturaleza. [26] Preston respondió a la crítica de Maxwell argumentando que la energía cinética de cada partícula simple individual podría hacerse arbitrariamente baja postulando una masa suficientemente baja (y una densidad numérica más alta) para las partículas. Pero esta cuestión fue discutida más tarde de manera más detallada por Poincaré , quien demostró que el problema termodinámico dentro de los modelos de Le Sage seguía sin resolverse.
Caspar Isenkrahe presentó su modelo en diversas publicaciones entre 1879 y 1915. [28] Sus supuestos básicos eran muy similares a los de Le Sage y Preston, pero dio una aplicación más detallada de la teoría cinética. Sin embargo, al afirmar que la velocidad de los corpúsculos después de la colisión se redujo sin ningún aumento correspondiente en la energía de ningún otro objeto, su modelo violó la conservación de la energía. Observó que existe una conexión entre el peso de un cuerpo y su densidad (porque cualquier disminución en la densidad de un objeto reduce el blindaje interno), por lo que continuó afirmando que los cuerpos cálidos deberían ser más pesados que los más fríos (relacionado con el efecto de la expansión térmica ).
En otro modelo, Adalbert Ryšánek en 1887 [29] también realizó un análisis cuidadoso, incluyendo una aplicación de la ley de Maxwell de las velocidades de las partículas en un gas. Distinguió entre un éter gravitacional y uno luminífero . Esta separación de esos dos medios era necesaria, porque según sus cálculos la ausencia de cualquier efecto de arrastre en la órbita de Neptuno implica un límite inferior para la velocidad de las partículas de 5 · 10 19 cm/s. Él (como Leray) argumentó que la energía absorbida se convierte en calor, que podría transferirse al éter luminífero y/o es utilizado por las estrellas para mantener su producción de energía. Sin embargo, estas sugerencias cualitativas no estaban respaldadas por ninguna evaluación cuantitativa de la cantidad de calor realmente producido.
En 1888, Paul du Bois-Reymond argumentó en contra del modelo de Le Sage, en parte porque la fuerza de gravedad predicha en la teoría de Le Sage no es estrictamente proporcional a la masa. Para lograr una proporcionalidad de masa exacta como en la teoría de Newton (que implica la ausencia de efectos de protección o saturación y una estructura de materia infinitamente porosa), el flujo ultramundano debe ser infinitamente intenso. Du Bois-Reymond rechazó esto por absurdo. Además, du Bois-Reymond, al igual que Kant, observó que la teoría de Le Sage no puede cumplir su objetivo, porque invoca conceptos como "elasticidad" y "dureza absoluta", etc., que (en su opinión) solo pueden explicarse por medio de fuerzas de atracción. El mismo problema surge para las fuerzas de cohesión en las moléculas. Como resultado, la intención básica de tales modelos, que es prescindir de las fuerzas elementales de atracción, es imposible. [30]
En 1863, François Antoine Edouard y Em. Keller [31] presentaron una teoría utilizando un mecanismo tipo Le Sage en combinación con ondas longitudinales del éter. Supusieron que esas ondas se propagan en todas direcciones y pierden parte de su momento después del impacto en los cuerpos, por lo que entre dos cuerpos la presión ejercida por las ondas es más débil que la presión que los rodea. En 1869, Paul-Emile Lecoq de Boisbaudran [32] presentó el mismo modelo que Leray (incluyendo la absorción y la producción de calor, etc.), pero al igual que Keller y Keller, reemplazó las partículas por ondas longitudinales del éter.

Después de estos intentos, otros autores, a principios del siglo XX, sustituyeron las partículas de Le Sage por la radiación electromagnética , en relación con la teoría del éter de Lorentz y la teoría del electrón de la época, en la que se suponía la constitución eléctrica de la materia.
En 1900 Hendrik Lorentz [33] escribió que el modelo de partículas de Le Sage no es coherente con la teoría electrónica de su tiempo. Pero la constatación de que los trenes de ondas electromagnéticas podían producir cierta presión, en combinación con el poder de penetración de los rayos Röntgen (ahora llamados rayos X ), lo llevó a concluir que nada contradice la posible existencia de una radiación aún más penetrante que los rayos X, que podría reemplazar a las partículas de Le Sage. Lorentz demostró que una fuerza de atracción entre partículas cargadas (que podría tomarse para modelar las subunidades elementales de la materia) surgiría de hecho, pero solo si la energía incidente se absorbiera por completo. Este era el mismo problema fundamental que había afectado a los modelos de partículas. Así que Lorentz escribió:
Pero la circunstancia de que esta atracción sólo podría existir si, de algún modo, la energía electromagnética desapareciera continuamente es una dificultad tan grave que no se puede considerar que lo que se ha dicho proporcione una explicación de la gravitación. Y no es ésta la única objeción que se puede plantear. Si el mecanismo de la gravitación consistiera en vibraciones que atraviesan el éter con la velocidad de la luz, la atracción debería ser modificada por el movimiento de los cuerpos celestes en una medida mucho mayor de lo que permiten admitir las observaciones astronómicas.
En 1922 [34] Lorentz examinó por primera vez la investigación de Martin Knudsen sobre los gases enrarecidos y en relación con ello discutió el modelo de partículas de Le Sage, seguido de un resumen de su propio modelo electromagnético de Le Sage, pero repitió su conclusión de 1900: Sin absorción no hay efecto gravitacional.
En 1913, David Hilbert se refirió a la teoría de Lorentz y la criticó argumentando que ninguna fuerza en la forma 1/r 2 puede surgir si la distancia mutua de los átomos es lo suficientemente grande en comparación con su longitud de onda. [35]
En 1904, JJ Thomson [36] consideró un modelo de tipo Le Sage en el que el flujo ultramundano primario consistía en una forma hipotética de radiación mucho más penetrante incluso que los rayos X. Sostuvo que el problema del calor de Maxwell podría evitarse suponiendo que la energía absorbida no se convierte en calor, sino que se vuelve a irradiar en una forma aún más penetrante. Observó que este proceso posiblemente puede explicar de dónde proviene la energía de las sustancias radiactivas; sin embargo, afirmó que es más probable que exista una causa interna de la radiactividad . En 1911, Thomson volvió a este tema en su artículo "Materia" en la Encyclopædia Britannica Undécima Edición . [37] Allí afirmó que esta forma de radiación secundaria es algo análoga a cómo el paso de partículas electrificadas a través de la materia causa la radiación de los rayos X aún más penetrantes. Observó:
Es un resultado muy interesante de los descubrimientos recientes que la maquinaria que Le Sage introdujo para el propósito de su teoría tiene una analogía muy cercana con cosas para las cuales ahora tenemos evidencia experimental directa.... Los rayos Röntgen, sin embargo, cuando son absorbidos no dan lugar, hasta donde sabemos, a rayos Röntgen más penetrantes como deberían para explicar la atracción, sino a rayos menos penetrantes o a rayos del mismo tipo. [37]
A diferencia de Lorentz y Thomson, Thomas Tommasina [38] propuso entre 1903 y 1928 la radiación de longitud de onda larga para explicar la gravedad, y la radiación de longitud de onda corta para explicar las fuerzas de cohesión de la materia. Charles F. Brush [39] también propuso en 1911 la radiación de longitud de onda larga, pero más tarde revisó su punto de vista y cambió a longitudes de onda extremadamente cortas.
En 1905, George Darwin calculó posteriormente la fuerza gravitatoria entre dos cuerpos a una distancia extremadamente cercana para determinar si los efectos geométricos conducirían a una desviación de la ley de Newton. [40] En este caso, Darwin reemplazó las unidades de materia ordinaria en forma de jaula de Le Sage por esferas duras microscópicas de tamaño uniforme. Concluyó que solo en el caso de colisiones perfectamente inelásticas (reflexión cero) se mantendría la ley de Newton, reforzando así el problema termodinámico de la teoría de Le Sage. Además, dicha teoría solo es válida si los componentes normal y tangencial del impacto son totalmente inelásticos (contrariamente al mecanismo de dispersión de Le Sage) y las partículas elementales son exactamente del mismo tamaño. Continuó diciendo que la emisión de luz es exactamente la inversa de la absorción de las partículas de Le Sage. Un cuerpo con diferentes temperaturas superficiales se moverá en la dirección de la parte más fría. En una revisión posterior de las teorías gravitacionales, Darwin describió brevemente la teoría de Le Sage y dijo que le dio una consideración seria, pero luego escribió:
No me referiré más a esta concepción, salvo para decir que creo que ningún hombre de ciencia está dispuesto a aceptarla como el camino verdadero. [41]

En 1908, Henri Poincaré realizó una crítica importante basándose parcialmente en los cálculos de Darwin. [42] Concluyó que la atracción es proporcional a , donde S es la superficie molecular de la Tierra, v es la velocidad de las partículas y ρ es la densidad del medio. Siguiendo a Laplace, argumentó que para mantener la proporcionalidad de la masa, el límite superior de S es como máximo una diezmillonésima parte de la superficie de la Tierra. Ahora bien, la resistencia del medio es proporcional a Sρv y, por tanto, la relación entre la resistencia y la atracción es inversamente proporcional a Sv . Para reducir la resistencia, Poincaré calculó un límite inferior para v = 24 · 10 17 veces la velocidad de la luz. Por tanto, hay límites inferiores para Sv y v, y un límite superior para S y con esos valores se puede calcular el calor producido, que es proporcional a Sρv 3 . El cálculo muestra que la temperatura de la Tierra aumentaría en 10 26 grados por segundo. Poincaré se dio cuenta de que "la Tierra no podría soportar por mucho tiempo un régimen así". También analizó algunos modelos de ondas (Tommasina y Lorentz), y observó que presentaban los mismos problemas que los modelos de partículas. Para reducir la resistencia, eran necesarias velocidades de onda superlumínicas, y seguirían estando sujetos al problema del calentamiento. Después de describir un modelo de re-radiación similar al de Thomson, concluyó: "Tales son las hipótesis complicadas a las que nos vemos llevados cuando tratamos de hacer sostenible la teoría de Le Sage" .
También afirmó que si en el modelo de Lorentz la energía absorbida se convierte completamente en calor, eso elevaría la temperatura de la Tierra en 10 13 grados por segundo. A continuación, Poincaré consideró la teoría de Le Sage en el contexto de la "nueva dinámica" que se había desarrollado a finales del siglo XIX y principios del XX, reconociendo específicamente el principio de relatividad. Para una teoría de partículas, señaló que " es difícil imaginar una ley de colisión compatible con el principio de relatividad ", y los problemas de arrastre y calentamiento siguen vigentes.
Una predicción básica de la teoría es la extrema porosidad de la materia. Como supusieron Fatio y Le Sage en 1690/1758 (y antes de ellos, Huygens), la materia debe consistir principalmente en espacio vacío para que las partículas muy pequeñas puedan penetrar en los cuerpos casi sin perturbaciones y, por lo tanto, cada parte de la materia pueda participar en la interacción gravitatoria. Esta predicción se ha confirmado (en algunos aspectos) con el transcurso del tiempo. De hecho, la materia consiste principalmente en espacio vacío y ciertas partículas como los neutrinos pueden atravesar la materia casi sin obstáculos. Sin embargo, la imagen de las partículas elementales como entidades clásicas que interactúan directamente, determinadas por sus formas y tamaños (en el sentido de la estructura de red propuesta por Fatio/Le Sage y las esferas de tamaño equivalente de Isenkrahe/Darwin), no es coherente con la comprensión actual de las partículas elementales. La propuesta de Lorentz/Thomson de partículas cargadas eléctricamente como los constituyentes básicos de la materia también es incompatible con la física actual.
Todo modelo de tipo Le Sage presupone la existencia de un flujo o radiación isótropa que llena el espacio, de enorme intensidad y capacidad de penetración. Esto tiene cierta similitud con la radiación cósmica de fondo de microondas (CMBR) descubierta en el siglo XX. La CMBR es, en efecto, un flujo que llena el espacio y bastante isótropo, pero su intensidad es extremadamente pequeña, al igual que su capacidad de penetración. El flujo de neutrinos, que emana del sol (por ejemplo) , posee las propiedades de penetración previstas por Le Sage para sus corpúsculos ultramundanos, pero este flujo no es isótropo (ya que las estrellas individuales son las principales fuentes de neutrinos) y la intensidad es incluso menor que la de la CMBR. Por supuesto, ni la CMBR ni los neutrinos se propagan a velocidades superlumínicas, que es otro atributo necesario de las partículas de Le Sage. Desde un punto de vista más moderno, descartando el simple concepto de “empuje” de Le Sage, la sugerencia de que el neutrino (o alguna otra partícula similar al neutrino) podría ser la partícula mediadora en una teoría cuántica de campo de la gravitación fue considerada y refutada por Feynman. [43]
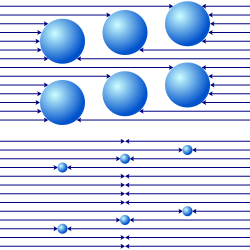
Aunque se postula que la materia es muy escasa en la teoría de Fatio-Le Sage, no puede ser perfectamente transparente, porque en ese caso no existiría ninguna fuerza gravitatoria. Sin embargo, la falta de transparencia perfecta conduce a problemas: con suficiente masa, la cantidad de sombreado producido por dos piezas de materia se vuelve menor que la suma del sombreado que cada una de ellas produciría por separado, debido a la superposición de sus sombras (P10, arriba). Este efecto hipotético, llamado apantallamiento gravitatorio , implica que la adición de materia no da como resultado un aumento proporcional directo en la masa gravitatoria. Por lo tanto, para que sea viable, Fatio y Le Sage postularon que el efecto de apantallamiento es tan pequeño que es indetectable, lo que requiere que la sección transversal de interacción de la materia debe ser extremadamente pequeña (P10, abajo). Esto coloca un límite inferior extremadamente alto en la intensidad del flujo requerido para producir la fuerza de gravedad observada. Cualquier forma de protección gravitacional representaría una violación del principio de equivalencia y sería inconsistente con el resultado nulo extremadamente preciso observado en el experimento de Eötvös y sus sucesores, todos los cuales han confirmado en cambio la equivalencia precisa de la masa gravitacional activa y pasiva con la masa inercial que fue predicha por la relatividad general . [44] Para obtener más información histórica sobre la conexión entre la protección gravitacional y la gravedad de Le Sage, consulte Martins, [45] [46] y Borzeszkowski et al. [47]
Dado que la propuesta de Isenkrahe sobre la conexión entre densidad, temperatura y peso se basaba puramente en los efectos previstos de los cambios en la densidad del material , y dado que la temperatura a una densidad dada puede aumentarse o disminuirse, los comentarios de Isenkrahe no implican ninguna relación fundamental entre temperatura y gravitación. (En realidad, existe una relación entre temperatura y gravitación, así como entre energía de enlace y gravitación, pero estos efectos reales no tienen nada que ver con la propuesta de Isenkrahe. Véase la sección siguiente sobre "Acoplamiento a la energía"). En cuanto a la predicción de una relación entre gravitación y densidad, toda la evidencia experimental indica que no existe tal relación.
Según la teoría de Le Sage, un cuerpo aislado está sujeto a arrastre si está en movimiento con respecto al único marco isótropo del flujo ultramundano (es decir, el marco en el que la velocidad de los corpúsculos ultramundanos es la misma en todas las direcciones). Esto se debe al hecho de que, si un cuerpo está en movimiento, las partículas que golpean el cuerpo desde el frente tienen una velocidad mayor (en relación con el cuerpo) que las que golpean el cuerpo desde atrás; este efecto actuará para disminuir la distancia entre el sol y la tierra. La magnitud de este arrastre es proporcional a vu , donde v es la velocidad de las partículas y u es la velocidad del cuerpo, mientras que la fuerza característica de la gravedad es proporcional a v 2 , por lo que la relación entre el arrastre y la fuerza gravitatoria es proporcional a u / v . Por lo tanto, para una fuerza característica dada de la gravedad, la cantidad de arrastre para una velocidad dada u se puede hacer arbitrariamente pequeña aumentando la velocidad v de los corpúsculos ultramundanos. Sin embargo, para reducir la resistencia a un nivel aceptable (es decir, consistente con la observación) en términos de la mecánica clásica, la velocidad v debe ser muchos órdenes de magnitud mayor que la velocidad de la luz . Esto hace que la teoría de Le Sage sea fundamentalmente incompatible con la ciencia moderna de la mecánica basada en la relatividad especial , según la cual ninguna partícula (u onda) puede superar la velocidad de la luz. Además, incluso si las partículas superlumínicas fueran posibles, la temperatura efectiva de un flujo de este tipo sería suficiente para incinerar toda la materia ordinaria en una fracción de segundo.
Como demostró Laplace, otro posible efecto Le Sage es la aberración orbital debida a la velocidad finita de la gravedad . A menos que las partículas de Le Sage se muevan a velocidades mucho mayores que la velocidad de la luz, como supusieron Le Sage y Kelvin, existe un retraso temporal en las interacciones entre los cuerpos (el tiempo de tránsito). En el caso del movimiento orbital, esto da como resultado que cada cuerpo reaccione a una posición retardada del otro, lo que crea un componente de fuerza principal. Al contrario del efecto de arrastre, este componente actuará para acelerar ambos objetos alejándolos uno del otro. Para mantener órbitas estables, el efecto de la gravedad debe propagarse mucho más rápido que la velocidad de la luz o no debe ser una fuerza puramente central. Muchos han sugerido esto como una refutación concluyente de cualquier tipo de teoría de Le Sage. En contraste, la relatividad general es consistente con la falta de aberración apreciable identificada por Laplace, porque aunque la gravedad se propaga a la velocidad de la luz en la relatividad general, la aberración esperada se cancela casi exactamente por los términos dependientes de la velocidad en la interacción. [48]
En muchos modelos de partículas, como el de Kelvin, el rango de gravedad está limitado debido a la naturaleza de las interacciones de las partículas entre sí. El rango está determinado efectivamente por la velocidad con la que los modos internos propuestos de las partículas pueden eliminar los defectos de momento ( sombras ) que se crean al atravesar la materia. Tales predicciones en cuanto al rango efectivo de gravedad variarán y dependen de los aspectos y supuestos específicos en cuanto a los modos de interacción que están disponibles durante las interacciones de partículas. Sin embargo, para esta clase de modelos, la estructura observada a gran escala del cosmos restringe dicha dispersión a aquellos que permitirán la agregación de tales inmensas estructuras gravitacionales.
Como se señaló en la sección histórica, un problema importante para todos los modelos de Le Sage es la cuestión de la energía y el calor . Como demostraron Maxwell y Poincaré, las colisiones inelásticas conducen a una vaporización de la materia en fracciones de segundo y las soluciones propuestas no eran convincentes. Por ejemplo, Aronson [27] proporcionó una prueba sencilla de la afirmación de Maxwell:
Supongamos que, contrariamente a la hipótesis de Maxwell, las moléculas de materia bruta poseen en realidad más energía que las partículas. En ese caso, las partículas, en promedio, ganarían energía en la colisión y las partículas interceptadas por el cuerpo B serían reemplazadas por otras más energéticas que rebotarían en el cuerpo B. Así, el efecto de la gravedad se invertiría: habría una repulsión mutua entre todos los cuerpos de materia mundana, contrariamente a lo observado. Si, por otra parte, las energías cinéticas promedio de las partículas y de las moléculas son las mismas, entonces no se produciría una transferencia neta de energía y las colisiones serían equivalentes a las elásticas, que, como se ha demostrado, no producen una fuerza gravitatoria.
Del mismo modo, la violación de la ley de conservación de la energía por parte de Isenkrahe es inaceptable, y la aplicación que hace Kelvin del teorema de Clausius conduce (como señaló el propio Kelvin) a una especie de mecanismo de movimiento perpetuo . La sugerencia de un mecanismo de re-radiación secundaria para los modelos de ondas atrajo el interés de JJ Thomson, pero no fue tomada muy en serio ni por Maxwell ni por Poincaré, porque implica una grave violación de la segunda ley de la termodinámica (enormes cantidades de energía que se convierten espontáneamente de una forma más fría a una más caliente), que es una de las leyes físicas más sólidamente establecidas.
El problema de la energía también se ha considerado en relación con la idea de la acreción de masa en conexión con la teoría de la Tierra en expansión . Entre los primeros teóricos que vincularon el aumento de masa en algún tipo de modelo de gravedad de empuje con la expansión de la Tierra estaban Yarkovsky y Hilgenberg. [49] La idea de la acreción de masa y la teoría de la Tierra en expansión no son consideradas actualmente como viables por los científicos convencionales. Esto se debe, entre otras razones, a que, según el principio de equivalencia masa-energía , si la Tierra estuviera absorbiendo la energía del flujo ultramundano a la velocidad necesaria para producir la fuerza de gravedad observada (es decir, utilizando los valores calculados por Poincaré), su masa se duplicaría en cada fracción de segundo.
Basándose en la evidencia observacional , ahora se sabe que la gravedad interactúa con todas las formas de energía , y no solo con la masa. La energía de enlace electrostático del núcleo, la energía de las interacciones débiles en el núcleo y la energía cinética de los electrones en los átomos, todas contribuyen a la masa gravitatoria de un átomo, como se ha confirmado con alta precisión en experimentos de tipo Eötvös . [50] Esto significa, por ejemplo, que cuando los átomos de una cantidad de gas se mueven más rápidamente, la gravitación de ese gas aumenta. Además, los experimentos de medición de distancia por láser lunar han demostrado que incluso la energía de enlace gravitatorio en sí misma también gravita, con una fuerza consistente con el principio de equivalencia de alta precisión, lo que demuestra además que cualquier teoría exitosa de la gravitación debe ser no lineal y autoacoplada. [51] [52] La teoría de Le Sage no predice ninguno de estos efectos antes mencionados, ni tampoco ninguna de las variantes conocidas de la teoría de Le Sage.
Lyman Spitzer calculó en 1941 [53] que la absorción de radiación entre dos partículas de polvo produce una fuerza de atracción neta que varía proporcionalmente a 1/ r 2 (evidentemente desconocía el mecanismo de sombra de Le Sage y, especialmente, las consideraciones de Lorentz sobre la presión de radiación y la gravedad). George Gamow , que llamó a este efecto "gravedad simulada", propuso en 1949 [54] que después del Big Bang la temperatura de los electrones descendió más rápido que la temperatura de la radiación de fondo. La absorción de radiación produjo un mecanismo de Lesage entre electrones, que podría haber tenido un papel importante en el proceso de formación de galaxias poco después del Big Bang . Sin embargo, esta propuesta fue refutada por Field en 1971 [55], quien demostró que este efecto era demasiado pequeño, porque los electrones y la radiación de fondo estaban casi en equilibrio térmico. Hogan y White propusieron en 1986 [56] que la gravedad simulada podría haber influido en la formación de galaxias mediante la absorción de la luz estelar pregaláctica. Pero Wang y Field [57] demostraron que cualquier forma de gravedad simulada es incapaz de producir suficiente fuerza para influir en la formación de galaxias.
El mecanismo de Le Sage también ha sido identificado como un factor significativo en el comportamiento del plasma polvoriento . AM Ignatov [58] ha demostrado que surge una fuerza de atracción entre dos granos de polvo suspendidos en un plasma isotrópico sin colisiones debido a colisiones inelásticas entre los iones del plasma y los granos de polvo. Esta fuerza de atracción es inversamente proporcional al cuadrado de la distancia entre los granos de polvo y puede contrarrestar la repulsión de Coulomb entre los granos de polvo.
En la teoría cuántica de campos se propone la existencia de partículas virtuales , que dan lugar al llamado efecto Casimir . Casimir calculó que entre dos placas solo se deben tener en cuenta las partículas con longitudes de onda específicas a la hora de calcular la energía del vacío . Por tanto, la densidad de energía entre las placas es menor si las placas están próximas entre sí, lo que da lugar a una fuerza de atracción neta entre las placas. Sin embargo, el marco conceptual de este efecto es muy diferente de la teoría de Fatio y Le Sage.
La revisión de la teoría de Le Sage en el siglo XIX identificó varios problemas estrechamente relacionados con la teoría, relacionados con el calentamiento excesivo, la fricción, el apantallamiento y la aberración gravitacional. El reconocimiento de estos problemas, junto con un alejamiento general de las teorías basadas en la mecánica, resultó en una pérdida progresiva de interés en la teoría de Le Sage. Finalmente, en el siglo XX, la teoría de Le Sage fue eclipsada por la teoría de la relatividad general de Einstein .
En 1965, Richard Feynman examinó el mecanismo de Fatio/Lesage, principalmente como un ejemplo de un intento de explicar una ley física "complicada" (en este caso, la ley de la gravedad del cuadrado inverso de Newton) en términos de operaciones primitivas más simples sin el uso de matemáticas complejas, y también como un ejemplo de una teoría fallida. Señala que el mecanismo de "partículas que rebotan" reproduce la ley de fuerza del cuadrado inverso y que "la extrañeza de la relación matemática se reducirá mucho" , pero luego comenta que el esquema "no funciona" , debido al arrastre que predice que experimentarían los cuerpos en movimiento. [59] [60]
Hay intentos ocasionales de rehabilitar la teoría fuera de la corriente principal, incluidos los de Radzievskii y Kagalnikova (1960), [61] Shneiderov (1961), [62] Buonomano y Engels (1976), [63] Adamut (1982), [64] Popescu (1982), [65] Jaakkola (1996), [66] Tom Van Flandern (1999), [67] y Edwards (2014). [68]
En Edwards et al. se analizan diversos modelos de Le Sage y temas relacionados. [69] [70] [71] [72]
{{cite book}}: |periodical=ignorado ( ayuda ){{cite book}}: |journal=ignorado ( ayuda ){{cite book}}: |periodical=ignorado ( ayuda ){{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace ){{citation}}: Falta o está vacío |title=( ayuda ){{citation}}: CS1 maint: varios nombres: lista de autores ( enlace ){{citation}}: CS1 maint: varios nombres: lista de autores ( enlace ){{citation}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace )