Isometría del plano euclidiano
Existen cuatro tipos de isometrías no triviales (la identidad también lo es): traslación, simetría, rotación y reflexión con deslizamiento.
Sin embargo, doblar, cortar o derretir la hoja de plástico no son consideradas isometrías.
Una manera de ver esto es que tanto las simetrías como las rotaciones tienen puntos fijos, mientras que la reflexión con desplazamiento no, por lo que no puede corresponderse con ninguna de estas; tampoco puede ser una traslación, porque en una traslación todos los puntos se desplazan en la misma dirección y, sin embargo, en la reflexión son desplazamiento, un punto del eje se desplaza en la dirección del eje y un punto fuera del eje, no.
La traslación es una isometría que realiza un cambio de posición o lugar en el espacio, manteniendo las direcciones (medidas angulares y longitudinales) de todos los elementos del espacio, dicha traslación puede ser determinadas por un vector o por dos puntos (el origen y el destino).
b) El punto, su imagen y el centro de simetría pertenezcan a una misma recta.
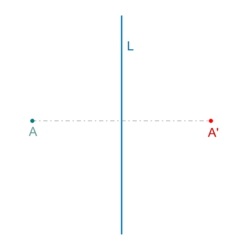
b) El segmento que une un punto con su imagen, es perpendicular al eje de simetría.
En la simetría axial se conservan las distancias pero no la dirección de los ángulos.
Por ejemplo, componiendo simetrías se pueden obtiener todas las isometrías de los ejemplos anteriores: En el apartado anterior hemos visto los siguientes ejemplos de isometrías: la identidad, las traslaciones, las simetrías y las rotaciones, y hemos visto que al componerlas entre sí volvíamos a obtener una isometría.
Es decir, no hay más isometrías del plano que la identidad, las traslaciones, las simetrías, las rotaciones y las reflexiones deslizadas.
En particular, al componer dos cualesquiera de ellas, no sólo obtendremos una isometría (que no sabemos cómo puede transformar exactamente el espacio), sino que volveremos a obtener la identidad, una traslación, una simetría, una rotación o una reflexión deslizada, y sabemos cómo estas transforman globalmente el plano.
Esto se traduce en que las isometrías del plano, con la composición como operación, son un grupo generado por las simetrías.