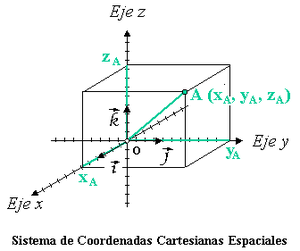
Sistema de coordenadas

[2]​ En geometría, las coordenadas son valores numéricos que determinan la posición de un punto en un plano o en el espacio.En el espacio euclídeo tridiomensional según el sistema de Descartes, la posición de un punto está determinada si se especifican las distancias a tres planos de coordenadas que se cruzan en un punto en ángulo recto entre sí.Sin embargo estas formas de especificar un punto no son las únicas posibles, las coordenadas polares en el plano o las coordenadas esféricas (donde el origen está en el centro de una serie de esferas) o las coordenadas cilíndricas en el espacio son otras formas que requieren especificar menos distancias y más ángulos de orientación.En geografía, las coordenadas se eligen como un sistema de coordenadas aproximadamente esférico: latitud, longitud y altura por encima de un nivel general conocido (como por ejemplo, el del océano).Este sistema de coordenadas es esencial para la ubicación precisa en la superficie terrestre y se utiliza en cartografía, navegación, topografía y en tecnologías GNSS (Sistema Global de Navegación por Satélite), proporcionando una base sólida para la representación geoespacial y la geolocalización precisa de lugares en todo el mundo.La resolución de numerosos problemas matemáticos o físicos implica elegir aquel sistema de coordenadas específico en el que el problema se resuelva más fácil o más conveniente en cada caso particular.En la práctica, se utilizan varios sistemas de coordenadas celestes.Nótese que por ejemplo de acuerdo a la cosmología moderna la forma del espacio-tiempo es un espacio curvado por lo que en el universo no siempre sería posible usar coordenadas cartesianas.Es el conjunto de los números reales representado gráficamente por una recta en la que se pueden ubicar todos los números naturales, enteros, fraccionarios, decimales, etc.[3]​ Cada punto de la recta representa un número real, ya sea mediante una correspondencia biunívoca o mediante una aplicación biyectiva, usada para representar los números como puntos especialmente marcados, como por ejemplo los números enteros mediante una recta llamada recta graduada como la entera[3]​ de puntos ordenados y separados entre sí a la misma distancia.[4]​ Para representar un número de la recta real se emplean las letras mayúsculas y sus coordenadas correspondientes, por ejemplo, los puntos A(5), B(3), C(-3), D(-5),etc.En un espacio euclídeo, un sistema de coordenadas cartesianas se define por dos o tres ejes ortogonales igualmente escalados, dependiendo de si es un sistema bidimensional o tridimensional (análogamente enLas coordenadas polares son un sistema de coordenadas bidimensional en el que cada punto o posición del plano se determina mediante un ángulo y una distancia.(medido en sentido contrario al de las agujas del reloj desde el eje hasta la línea).son todas coordenadas polares para el mismo punto.Las coordenadas logarítmicas están estrechamente conectadas con las coordenadas polares, que generalmente se usan para describir dominios en el plano con algún tipo de simetría rotacional.se usa para representar los puntos de un espacio euclídeo tridimensional.Este sistema de coordenadas esféricas está formado por tres ejes mutuamente ortogonales que se cortan en el origen., se puede construir un sistema de coordenadas curvilíneo local en torno a un puntoCuando eso sucede muchas de las fórmulas del cálculo vectorial diferencial se pueden escribir de forma particularmente simple en esas coordenadas, pudiéndose aprovechar ese hecho cuando existe por ejemplo simetría axial, esférica o de otro tipo fácilmente representable en esas coordenadas curvilíneas ortogonales.Su notación en forma matricial se emplea en bibliotecas de programación gráfica en 3D como OpenGL y Direct3D.Esto implica la consideración de los puntos impropios, o del infinito.Un punto impropio es aquel donde λ = 0, y está determinado por la dirección de una recta, contenida en el plano proyectivo.Por ejemplo, las coordenadas plückerianas permiten determinar la posición de una línea recta en el espacio.Los dos sistemas en un caso como este se dice que son duales.Los sistemas duales tienen la propiedad de que los resultados de un sistema pueden trasladarse al otro, ya que estos resultados son solo interpretaciones diferentes del mismo resultado analítico; esto se conoce como el principio de dualidad.En esencia un cambio de coordenadas supone cambiar las variables de las que a depende el problema, a otras coordenadas diferentes en las que el problema puede tener una forma equivalente pero más simple, que permite encontrar la solución con mayor facilidad.Dado que a menudo existen muchos sistemas de coordenadas posibles para describir figuras geométricas, es importante entender cómo se relacionan.Este cambio de variable permite por ejemplo reescribir integrales del siguiente modo:Por ejemplo, las superficies de coordenadas que se obtienen manteniendo constante ρ en el sistema de coordenadas esféricas son las esferas con centro en el origen.Por ejemplo, en un sistema de coordenadas esféricas es suficiente con establecer el radio nulo