Aceleración

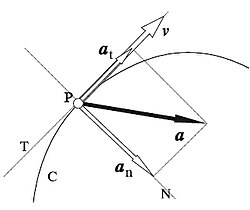
En el contexto de la mecánica vectorial newtoniana se representa normalmente porLas aceleraciones son cantidades vectoriales (en el sentido de que tienen magnitud y dirección).Por ejemplo, cuando un vehículo arranca estando detenido (velocidad cero, en un marco de referencia inercial) y viaja en línea recta a velocidades crecientes, está acelerando en la dirección de la marcha.Si el vehículo gira, se produce una aceleración hacia la nueva dirección y cambia su vector de movimiento.La aceleración del vehículo en su dirección actual de movimiento se llama aceleración lineal (o tangencial durante los movimientos circulares), la reacción que experimentan los pasajeros a bordo como una fuerza que los empuja hacia atrás en sus asientos.Al cambiar de dirección, la aceleración que efectúa se llama aceleración radial (ortogonal durante los movimientos circulares), la reacción que experimentan los pasajeros como una fuerza centrífuga.Si la velocidad del vehículo disminuye, esto es una aceleración en la dirección opuesta y matemáticamente negativa, a veces llamada desaceleración, y los pasajeros experimentan la reacción a la desaceleración como una fuerza inercial que los empuja hacia adelante.Estas aceleraciones negativas a menudo se logran mediante la combustión de retrocohetes en naves espaciales.Los pasajeros sienten cada una de estas aceleraciones (tangencial, radial, desaceleración) hasta que su velocidad relativa (diferencial) se neutraliza con respecto al vehículo.Según la mecánica newtoniana, una partícula no puede seguir una trayectoria curva a menos que sobre ella actúe una cierta aceleración como consecuencia de la acción de una fuerza, ya que si esta no existiese, su movimiento sería rectilíneo.Asimismo, una partícula en movimiento rectilíneo solo puede cambiar su velocidad bajo la acción de una aceleración en la misma dirección de su velocidad (dirigida en el mismo sentido si acelera; o en sentido contrario si desacelera).En la mecánica newtoniana, para un cuerpo con masa constante, la aceleración del cuerpo medida por un observador inercial es proporcional a la fuerza que actúa sobre el mismo (segunda ley de Newton):La relación anterior es válida en cualquier sistema de referencia inercial.Se siente esta tensión de manera similar al peso.La relación entre aceleración y esfuerzo es el dominio de la dinámica ; pero la aceleración es una noción de cinemática, es decir que se define solo a partir del movimiento, sin involucrar las fuerzas.Puesto que la velocidad instantánea v a su vez es la derivada del vector posición r respecto al tiempo, la aceleración es la derivada segunda de la posición con respecto del tiempo:Se puede obtener la velocidad a partir de la aceleración mediante integración:Los acelerómetros electrónicos son fabricados para medir la aceleración en una, dos o tres direcciones.Cuentan con dos elementos conductivos, separados por un material que varía su conductividad en función de las medidas, que a su vez serán relativas a la aceleración del conjunto.En tanto que el vector velocidad v es tangente a la trayectoria, el vector aceleración a puede descomponerse en dos componentes (llamadas componentes intrínsecas) mutuamente perpendiculares: una componente tangencial at (en la dirección de la tangente a la trayectoria), llamada aceleración tangencial, y una componente normal an (en la dirección de la normal principal a la trayectoria), llamada aceleración normal o centrípeta (este último nombre en razón a que siempre está dirigida hacia el centro de curvatura).el vector unitario tangente a la trayectoria en la misma dirección que la velocidad yLos vectores que aparecen en las expresiones anteriores son los vectores del triedro de Frênet que aparece en la geometría diferencial de curvas del siguiente modo: Un movimiento circular uniforme es aquel en el que la partícula recorre una trayectoria circular de radio R con rapidez constante, es decir, que la distancia recorrida en cada intervalo de tiempo igual es la misma.En este tipo de movimiento la aceleración aplicada al objeto se encarga de modificar la trayectoria del objeto y no en modificar su velocidad.Si se aplican las fórmulas anteriores al movimiento rectilíneo, en el que solo existe aceleración tangencial, al estar todos los vectores contenidos en la trayectoria, podemos prescindir de la notación vectorial y escribir simplemente:En teoría general de la relatividad el caso de la aceleración es más complicado, ya que debido a que el propio espacio-tiempo es curvo (ver curvatura del espacio-tiempo), una partícula sobre la que no actúa ninguna fuerza puede seguir una trayectoria curva, de hecho la línea curva que sigue una partícula sobre la que no actúa ninguna fuerza exterior es una línea geodésica, de hecho en relatividad general la fuerza gravitatoria no se interpreta como una fuerza sino como un efecto de la curvatura del espacio-tiempo que hace que las partículas no trayectorias rectas sino líneas geodéscias.En este contexto la aceleración no geodésica de una partícula es un vector cuyas cuatro componentes se calulan como:una partícula puede tener aceleración cero aunque su cuadrivelocidad no sea constante, eso sucede cuando la partícula sigue una línea geodésica de un espacio-tiempo de curvatura no nula.La ingeniería mecánica es el diseño y fabricación de máquinas, es decir, sistemas que realizan movimientos.Una parte importante es el dimensionamiento, es decir la elección de actuadores (gatos, motores) y piezas que soportan las fuerzas.En muchos casos, la especificación es "llevar un objeto del punto A al punto B en un tiempo t, con el tiempo t a veces expresado como una tasa (realizando el movimiento n veces por hora).