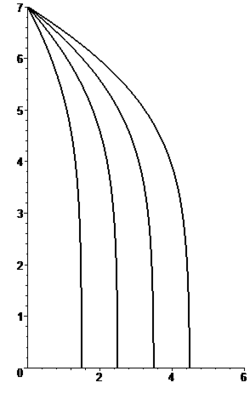
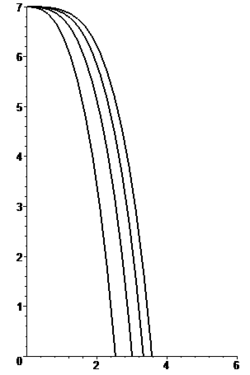
Caída libre
[1] Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también referirse coloquialmente a estas como caídas libres, aunque los efectos de la densidad del medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical (llama este movimiento como tiro vertical); o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste.
Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
[2][3] Un sistema de referencia ligado a un cuerpo en caída libre puede considerarse inercial o no inercial en función del marco teórico que se esté usando.
En la física clásica, la fuerza gravitatoria que se ejerce sobre una masa es proporcional a la intensidad del campo gravitatorio en la posición espacial donde se encuentre dicha masa.
En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica.
En la caída libre ideal, se desprecia la resistencia aerodinámica que presenta el aire al movimiento del cuerpo, analizando lo que pasaría en el vacío.
En esas condiciones, la aceleración que adquiriría el cuerpo sería debida exclusivamente a la gravedad, siendo independiente de su masa; por ejemplo, si dejáramos caer una bala de cañón y una pluma en el vacío, ambos adquirirían la misma aceleración,
considerando vertical el eje y, con el sentido positivo hacia arriba, la aceleración de la gravedad es vertical hacia abajo, por lo que la señalamos con signo negativo: la velocidad que alcanza el móvil tiempo
, entonces: para determinar la posición, cuota y, tenemos que: si tomamos
: En esta expresión se tiene en cuenta que se mide sobre el eje y, tomando el sentido positivo en sentido vertical hacia arriba, tanto la posición como la velocidad y se considera como negativo el sentido vertical hacia abajo en cuanto a la posición como en cuanto a la velocidad o aceleración.
que actúa sobre un cuerpo es igual al producto de su masa
en la misma dirección, y sentido opuesto a la velocidad.
lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.
El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la velocidad aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable).
La ecuación de movimiento se puede escribir en términos la altura y: (1)
Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:
Donde: La velocidad límite puede calcularse fácilmente poniendo igual a cero la aceleración en la ecuación (3):
La solución analítica de la ecuación diferencial (3) depende del signo relativo de la fuerza de rozamiento y el peso por lo que la solución analítica es diferente para un cuerpo que sube o para uno que cae.
Si se integran las ecuaciones anteriores para el caso de caída libre desde una altura
se obtienen los siguientes resultados para la altura del cuerpo: Caída libre (
hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de
Intuitivamente la diferencia de tiempos es clara, en el tiro hacia arriba la velocidad inicial es mayor por lo que la fuerza de rozamiento promedio a lo largo de la trayectoria también es mayor que la que se alcanza en tiro hacia abajo.
La ecuación de la trayectoria en coordenadas cartesianas viene dada por: (4)
La caída libre desde grandes alturas en un campo gravitatorio aproximadamente esférico, como es el caso del campo gravitatorio terrestre, requiere correcciones importantes ya que en ese caso ni la magnitud ni la dirección de la fuerza gravitatoria son constantes.
Concretamente para un campo gravitatorio newtoniano con simetría esférica, cuando podemos ignorar el rozamiento con la atmósfera, la trayectoria es un arco de elipse.
Para el caso particular de caída con velocidad inicial nula sin rozamiento desde una distancia
, la trayectoria es una línea recta y la expresión de la velocidad
del cuerpo que cae, en función de la distancia
al centro de atracción gravitatoria generado por la masa