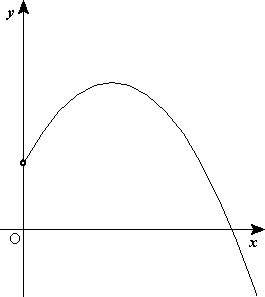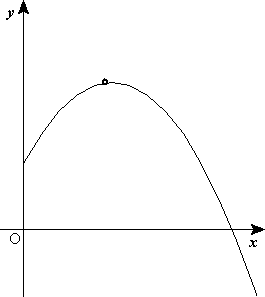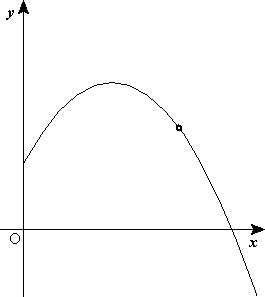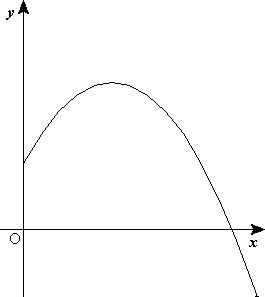
Trayectoria balística

La trayectoria balística es la trayectoria de vuelo que sigue un proyectil sometido únicamente a su propia inercia y a las fuerzas inherentes al medio en el que se desplaza, principalmente la fuerza gravitatoria.Cuando sobre el proyectil tan solo actúa la gravedad, la trayectoria balística es una parábola.Algunos proyectiles autopropulsados se denominan balísticos haciendo hincapié que no existe propulsión nada más que en la fase inicial de lanzamiento ('fase caliente').Utilizaremos las siguientes hipótesis simplificadoras: Supongamos que se dispara el proyectil con una velocidad inicial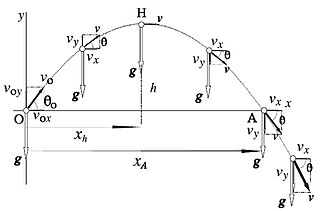En la figura 1 se observa que el vector velocidad inicialrespecto al eje x; el ánguloque forma la velocidad con la horizontal, que coincide con la pendiente de la trayectoria, cambia conforme avanza el proyectil.Integrando las ecuaciones (3) y teniendo en cuenta las condiciones iniciales (2) (4)Si eliminamos el tiempo entre las expresiones de las componentes x e y del vector de posición con las ecuaciones que dan las posiciones, obtendremos la ecuación algebraica de la trayectoria, esto es: (6)que representa una parábola en el plano x,y.En esa figura también se observa que la altura máxima en la trayectoria parabólica se producirá en H, cuando la componente vertical de la velocidadsea nula (máximo de la parábola); y que el alcance horizontalocurrirá cuando el cuerpo retorne al suelo, enA partir de las ecuaciones anteriores podemos obtener mucha información acerca del movimiento del proyectil.necesario para que el proyectil alcance la altura máximalo determinamos anulando la componente vertical de la velocidad en [4], ya que en ese punto la velocidad del proyectil es horizontal.alcanzada por el proyectil y el recorrido horizontalrealizado hasta ese instante los calculamos sustituyendo el tiempoen las componentes del vector de posiciónes la distancia horizontal cubierta durante ese tiempo y se determina sustituyendo el valor del tiempo de vuelo en, se obtiene el mismo alcance para un ángulo de disparo dado y para su complementario.En esas condiciones, el movimiento de una partícula en un campo gravitatorio uniforme no sigue estrictamente una parábola y es sólo casi-parabólico.En cuanto a la forma del rozamiento se distinguen dos casos.Para un fluido en reposo y un cuerpo moviéndose a muy baja velocidad, el flujo alrededor del cuerpo puede considerarse laminar y, en ese caso, el rozamiento es proporcional a la velocidad.La ecuación de la trayectoria resulta ser:donde: Para alturas suficientemente grandes el rozamiento del aire hace que el cuerpo caiga según una trayectoria cuyo último tramo es prácticamente vertical, al ser frenada casi completamente la velocidad horizontal inicial.A velocidades moderadamente grandes o grandes, o cuando el fluido está en movimiento, el flujo alrededor del cuerpo es turbulento y se producen remolinos y presiones que generan una fuerza de frenado proporcional al cuadrado de la velocidad.En lugar de las ecuaciones anteriores, más difíciles de integrar, se puede usar en forma aproximada las siguientes ecuaciones:Para esas ecuaciones la trayectoria viene dada por: