Espacio afín

En matemáticas , un espacio afín es una estructura geométrica que generaliza algunas de las propiedades de los espacios euclidianos de tal manera que estas son independientes de los conceptos de distancia y medida de ángulos , manteniendo únicamente las propiedades relacionadas con el paralelismo y la razón de longitudes para segmentos de rectas paralelas . El espacio afín es el escenario de la geometría afín .

Al igual que en el espacio euclidiano, los objetos fundamentales en un espacio afín se denominan puntos , que pueden considerarse como ubicaciones en el espacio sin ningún tamaño o forma: cero -dimensionales . A través de cualquier par de puntos se puede dibujar una línea recta infinita, un conjunto unidimensional de puntos; a través de tres puntos cualesquiera que no sean colineales, se puede dibujar un plano bidimensional ; y, en general, a través de $k + 1$ puntos en posición general, se puede dibujar un subespacio plano o afín $k$ -dimensional . El espacio afín se caracteriza por una noción de pares de líneas paralelas que se encuentran dentro del mismo plano pero nunca se encuentran entre sí (líneas no paralelas dentro del mismo plano se intersecan en un punto). Dada cualquier línea, se puede dibujar una línea paralela a ella a través de cualquier punto en el espacio, y se dice que la clase de equivalencia de líneas paralelas comparte una dirección .

A diferencia de los vectores en un espacio vectorial , en un espacio afín no hay un punto distinguido que sirva como origen . No existe un concepto predefinido de sumar o multiplicar puntos, o de multiplicar un punto por un número escalar. Sin embargo, para cualquier espacio afín, se puede construir un espacio vectorial asociado a partir de las diferencias entre los puntos inicial y final, que se denominan vectores libres , vectores de desplazamiento , vectores de traslación o simplemente traslaciones . ^[1] Del mismo modo, tiene sentido sumar un vector de desplazamiento a un punto de un espacio afín, lo que da como resultado un nuevo punto trasladado desde el punto inicial por ese vector. Si bien los puntos no se pueden sumar arbitrariamente, tiene sentido tomar combinaciones afines de puntos: sumas ponderadas con coeficientes numéricos que suman 1, lo que da como resultado otro punto. Estos coeficientes definen un sistema de coordenadas baricéntrico para el plano a través de los puntos.

Cualquier espacio vectorial puede ser visto como un espacio afín; esto equivale a "olvidar" el papel especial que desempeña el vector cero . En este caso, los elementos del espacio vectorial pueden verse como puntos del espacio afín o como vectores de desplazamiento o traslaciones . Cuando se considera como un punto, el vector cero se llama origen . La adición de un vector fijo a los elementos de un subespacio lineal (subespacio vectorial) de un espacio vectorial produce un subespacio afín del espacio vectorial. Se dice comúnmente que este subespacio afín se ha obtenido trasladando (alejándose del origen) el subespacio lineal por el vector de traslación (el vector añadido a todos los elementos del espacio lineal). En dimensiones finitas, un subespacio afín de este tipo es el conjunto solución de un sistema lineal no homogéneo . Los vectores de desplazamiento para ese espacio afín son las soluciones del sistema lineal homogéneo correspondiente , que es un subespacio lineal. Los subespacios lineales, por el contrario, siempre contienen el origen del espacio vectorial.

La dimensión de un espacio afín se define como la dimensión del espacio vectorial de sus traslaciones. Un espacio afín de dimensión uno es una línea afín . Un espacio afín de dimensión 2 es un plano afín . Un subespacio afín de dimensión $n - 1$ en un espacio afín o un espacio vectorial de dimensión $n$ es un hiperplano afín .

Descripción informal

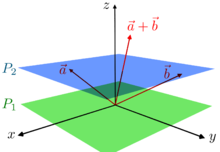
La siguiente caracterización puede ser más fácil de entender que la definición formal habitual: un espacio afín es lo que queda de un espacio vectorial después de que uno ha olvidado cuál punto es el origen (o, en palabras del matemático francés Marcel Berger , "Un espacio afín no es nada más que un espacio vectorial cuyo origen tratamos de olvidar, añadiendo traslaciones a las aplicaciones lineales" ^[2] ). Imaginemos que Alice sabe que un cierto punto es el origen real, pero Bob cree que otro punto, llamémoslo $p$ , es el origen. Se deben sumar dos vectores, $a$ y $b . Bob dibuja una flecha del punto$ $p$ al punto $a$ y otra flecha del punto $p$ al punto $b$ , y completa el paralelogramo para encontrar lo que Bob piensa que es $a + b$ , pero Alice sabe que en realidad ha calculado

p + (a - p) + (b - p)

De manera similar, Alice y Bob pueden evaluar cualquier combinación lineal de $a$ y $b$ , o de cualquier conjunto finito de vectores, y generalmente obtendrán respuestas diferentes. Sin embargo, si la suma de los coeficientes en una combinación lineal es 1, Alice y Bob llegarán a la misma respuesta.

Si Alicia viaja a

λa + (1 - λ) b

Entonces Bob puede viajar de manera similar a

p + λ(a - p) + (1 - λ)(b - p) = λ a + (1 - λ) b

Bajo esta condición, para todos los coeficientes $λ + (1 - λ) = 1$ , Alice y Bob describen el mismo punto con la misma combinación lineal, a pesar de utilizar orígenes diferentes.

Aunque sólo Alice conoce la "estructura lineal", tanto Alice como Bob conocen la "estructura afín", es decir, los valores de las combinaciones afines , definidas como combinaciones lineales en las que la suma de los coeficientes es 1. Un conjunto con una estructura afín es un espacio afín.

Definición

Si bien el espacio afín se puede definir axiomáticamente (ver § Axiomas a continuación), de manera análoga a la definición del espacio euclidiano implícita en los Elementos de Euclides , por conveniencia la mayoría de las fuentes modernas definen los espacios afines en términos de la bien desarrollada teoría del espacio vectorial.

Un espacio afín es un conjunto $A$ junto con un espacio vectorial , y una acción transitiva y libre del grupo aditivo de sobre el conjunto $A$ . ^[3] Los elementos del espacio afín $A$ se denominan puntos . Se dice que el espacio vectorial está asociado al espacio afín, y sus elementos se denominan vectores , traslaciones o, a veces, vectores libres . ${\overrightarrow {A}}$ ${\overrightarrow {A}}$ ${\overrightarrow {A}}$

Explícitamente, la definición anterior significa que la acción es un mapeo, generalmente denotado como una adición,

{\begin{aligned}A\times {\overrightarrow {A}}&\to A\\(a,v)\;&\mapsto a+v,\end{aligned}}

que tiene las siguientes propiedades. ^[4]^[5]^[6]

Identidad correcta :
$\forall a\in A,\;a+0=a$ , donde $0$ es el vector cero en ${\overrightarrow {A}}$
Asociatividad :
$\forall v,w\in {\overrightarrow {A}},\forall a\in A,\;(a+v)+w=a+(v+w)$ (aquí el último $+$ es la adición en ) ${\overrightarrow {A}}$
Acción libre y transitiva :
Para cada , la aplicación es una biyección . $a\in A$ ${\overrightarrow {A}}\to A\colon v\mapsto a+v$

Las dos primeras propiedades son simplemente propiedades definitorias de una acción grupal (correcta). La tercera propiedad caracteriza las acciones libres y transitivas, el carácter ontológico proviene de la transitividad, y luego el carácter inyectivo se desprende de la acción libre. Hay una cuarta propiedad que se desprende de los puntos 1 y 2 anteriores:

Existencia de traducciones uno a uno

Para todos , la aplicación es una biyección.

v\in {\overrightarrow {A}}

A\to A\colon a\mapsto a+v

La propiedad 3 se utiliza a menudo en la siguiente forma equivalente (la quinta propiedad).

Sustracción:

Para cada

a, b

A

, existe un único , denotado

b

-

a

, tal que .

v\in {\overrightarrow {A}}

b=a+v

Otra forma de expresar la definición es que un espacio afín es un espacio homogéneo principal para la acción del grupo aditivo de un espacio vectorial. Los espacios homogéneos están, por definición, dotados de una acción transitiva de grupo, y para un espacio homogéneo principal, dicha acción transitiva es, por definición, libre.

La sustracción y los axiomas de Weyl

Las propiedades de la acción de grupo permiten la definición de la resta para cualquier par ordenado $(b, a)$ de puntos en $A$ , lo que produce un vector de . Este vector, denotado como , se define como el único vector en tal que ${\overrightarrow {A}}$ $b-a$ ${\overrightarrow {ab}}$ ${\overrightarrow {A}}$

a+(b-a)=b.

La existencia se desprende de la transitividad de la acción, y la unicidad se desprende porque la acción es libre.

Esta resta tiene las dos propiedades siguientes, llamadas axiomas de Weyl : ^[7]

$\forall a\in A,\;\forall v\in {\overrightarrow {A}}$ , hay un punto único tal que $b\in A$ $b-a=v.$
$\forall a,b,c\in A,\;(c-b)+(b-a)=c-a.$

La propiedad del paralelogramo se cumple en espacios afines, donde se expresa como: dados cuatro puntos las igualdades y son equivalentes. Esto resulta del segundo axioma de Weyl, ya que $a,b,c,d,$ $b-a=d-c$ $c-a=d-b$ $d-a=(d-b)+(b-a)=(d-c)+(c-a).$

Los espacios afines pueden definirse de manera equivalente como un conjunto de puntos $A$ , junto con un espacio vectorial y una resta que satisface los axiomas de Weyl. En este caso, la adición de un vector a un punto se define a partir del primero de los axiomas de Weyl. ${\overrightarrow {A}}$

Subespacios afines y paralelismo

Un subespacio afín (también llamado, en algunos contextos, variedad lineal , plano o, sobre los números reales , variedad lineal ) $B$ de un espacio afín $A$ es un subconjunto de $A$ tal que, dado un punto , el conjunto de vectores es un subespacio lineal de . Esta propiedad, que no depende de la elección de $a$ , implica que $B$ es un espacio afín, que tiene como espacio vectorial asociado . $a\in B$ ${\overrightarrow {B}}=\{b-a\mid b\in B\}$ ${\overrightarrow {A}}$ ${\overrightarrow {B}}$

Los subespacios afines de $A$ son los subconjuntos de $A$ de la forma

a+V=\{a+w:w\in V\},

donde $a$ es un punto de $A$ , y $V$ un subespacio lineal de . ${\overrightarrow {A}}$

El subespacio lineal asociado con un subespacio afín a menudo se denomina sudirección , y se dice que dos subespacios que comparten la misma dirección sonparalelos.

Esto implica la siguiente generalización del axioma de Playfair : Dada una dirección $V$ , para cualquier punto $a$ de $A$ hay un y sólo un subespacio afín de dirección $V$ , que pasa por $a$ , es decir, el subespacio $a + V.$

Cada traducción asigna cualquier subespacio afín a un subespacio paralelo. $A\to A:a\mapsto a+v$

El término paralelo también se utiliza para dos subespacios afines tales que la dirección de uno está incluida en la dirección del otro.

Mapa afín

Dados dos espacios afines $A$ y $B$ cuyos espacios vectoriales asociados son y , una función afín o un homomorfismo afín de $A$ a $B$ es una función ${\overrightarrow {A}}$ ${\overrightarrow {B}}$

f:A\to B

de tal manera que

{\begin{aligned}{\overrightarrow {f}}:{\overrightarrow {A}}&\to {\overrightarrow {B}}\\b-a&\mapsto f(b)-f(a)\end{aligned}}

es una función lineal bien definida . Por estar bien definida se entiende que $b$ $-$ $a$ $=$ $d$ $-$ $c$ implica $f$ $($ $b$ $) -$ $f$ $($ $a$ $) =$ $f$ $($ $d$ $) -$ $f$ $($ $c$ $)$ . $f$

Esto implica que, para un punto y un vector , se tiene $a\in A$ $v\in {\overrightarrow {A}}$

f(a+v)=f(a)+{\overrightarrow {f}}(v).

Por lo tanto, dado que para cualquier $b$ dado en $A$ , $b = a + v$ para un $v$ único , $f$ está completamente definida por su valor en un solo punto y la función lineal asociada . ${\overrightarrow {f}}$

Endomorfismos

Una transformación afín o endomorfismo de un espacio afín es una función afín de ese espacio a sí mismo. Una familia importante de ejemplos son las traslaciones: dado un vector , la función de traslación que envía para cada in es una función afín. Otra familia importante de ejemplos son las funciones lineales centradas en un origen: dado un punto y una función lineal , se puede definir una función afín por para cada in . $A$ ${\overrightarrow {v}}$ $T_{\overrightarrow {v}}:A\rightarrow A$ $a\mapsto a+{\overrightarrow {v}}$ $a$ $A$ $b$ $M$ $L_{M,b}:A\rightarrow A$ $L_{M,b}(a)=b+M(a-b)$ $a$ $A$

Después de elegir el origen , cualquier mapa afín puede escribirse únicamente como una combinación de una traslación y un mapa lineal centrado en . $b$ $b$

Espacios vectoriales como espacios afines

Todo espacio vectorial $V$ puede considerarse como un espacio afín sobre sí mismo. Esto significa que cada elemento de $V$ puede considerarse como un punto o como un vector. Este espacio afín se denota a veces $(V, V)$ para enfatizar el doble papel de los elementos de $V$ . Cuando se considera como un punto, el vector cero se denota comúnmente $como o$ (u $O$ , cuando se usan letras mayúsculas para los puntos) y se llama origen .

Si $A$ es otro espacio afín sobre el mismo espacio vectorial (es decir ), la elección de cualquier punto $a$ en $A$ define un isomorfismo afín único, que es la identidad de $V$ y mapea $a$ en $o$ . En otras palabras, la elección de un origen $a$ en $A$ nos permite identificar $A$ y $($ $V$ $,$ $V$ $)$ hasta un isomorfismo canónico . La contrapartida de esta propiedad es que el espacio afín $A$ puede identificarse con el espacio vectorial $V$ en el que "se ha olvidado el lugar del origen". $V={\overrightarrow {A}}$

Relación con los espacios euclidianos

Definición de espacios euclidianos

Los espacios euclidianos (incluida la línea unidimensional, el plano bidimensional y el espacio tridimensional comúnmente estudiados en geometría elemental, así como análogos de dimensiones superiores) son espacios afines.

De hecho, en la mayoría de las definiciones modernas, un espacio euclidiano se define como un espacio afín, tal que el espacio vectorial asociado es un espacio producto interior real de dimensión finita, es decir, un espacio vectorial sobre los reales con una forma cuadrática definida positiva $q (x)$ . El producto interior de dos vectores $x$ e $y$ es el valor de la forma bilineal simétrica

x\cdot y={\frac {1}{2}}(q(x+y)-q(x)-q(y)).

La distancia euclidiana habitual entre dos puntos $A$ y $B$ es

d(A,B)={\sqrt {q(B-A)}}.

En la definición más antigua de espacios euclidianos a través de la geometría sintética , los vectores se definen como clases de equivalencia de pares ordenados de puntos bajo equipolencia (los pares $(A, B)$ y $(C, D)$ son equipolentes si los puntos $A, B, D, C$ (en este orden) forman un paralelogramo ). Es sencillo verificar que los vectores forman un espacio vectorial, el cuadrado de la distancia euclidiana es una forma cuadrática en el espacio de vectores y las dos definiciones de espacios euclidianos son equivalentes.

Propiedades afines

En geometría euclidiana , la frase común " propiedad afín " se refiere a una propiedad que se puede demostrar en espacios afines, es decir, se puede demostrar sin utilizar la forma cuadrática y su producto interno asociado. En otras palabras, una propiedad afín es una propiedad que no involucra longitudes ni ángulos. Ejemplos típicos son el paralelismo y la definición de una tangente . Un no-ejemplo es la definición de una normal .

Equivalentemente, una propiedad afín es una propiedad que es invariante bajo transformaciones afines del espacio euclidiano.

Combinaciones afines y baricentro

Sea $a 1, ..., a n$ una colección de $n$ puntos en un espacio afín, y $n$ elementos del cuerpo fundamental . $\lambda _{1},\dots ,\lambda _{n}$

Supóngase que . Para dos puntos cualesquiera $o$ y $o'$ se tiene $\lambda _{1}+\dots +\lambda _{n}=0$

\lambda _{1}{\overrightarrow {oa_{1}}}+\dots +\lambda _{n}{\overrightarrow {oa_{n}}}=\lambda _{1}{\overrightarrow {o'a_{1}}}+\dots +\lambda _{n}{\overrightarrow {o'a_{n}}}.

Por lo tanto, esta suma es independiente de la elección del origen, y el vector resultante puede denotarse

\lambda _{1}a_{1}+\dots +\lambda _{n}a_{n}.

Cuando se recupera la definición de la resta de puntos. $n=2,\lambda _{1}=1,\lambda _{2}=-1$

Supongamos ahora que los elementos del campo satisfacen . Para alguna elección de un origen $o$ , denotemos por el único punto tal que $\lambda _{1}+\dots +\lambda _{n}=1$ $g$

\lambda _{1}{\overrightarrow {oa_{1}}}+\dots +\lambda _{n}{\overrightarrow {oa_{n}}}={\overrightarrow {og}}.

Se puede demostrar que es independiente de la elección de $o$ . Por lo tanto, si $g$

\lambda _{1}+\dots +\lambda _{n}=1,

Uno puede escribir

g=\lambda _{1}a_{1}+\dots +\lambda _{n}a_{n}.

El punto se llama baricentro de los pesos . También se dice que es una combinación afín de los coeficientes . $g$ $a_{i}$ $\lambda _{i}$ $g$ $a_{i}$ $\lambda _{i}$

Ejemplos

Cuando los niños encuentran las respuestas a sumas como $4 + 3$ o $4 - 2$ contando hacia la derecha o hacia la izquierda en una línea numérica , están tratando la línea numérica como un espacio afín unidimensional.
El tiempo puede modelarse como un espacio afín unidimensional. Los puntos específicos en el tiempo (como una fecha en el calendario) son puntos en el espacio afín, mientras que las duraciones (como un número de días) son desplazamientos.
El espacio de energías es un espacio afín para , ya que a menudo no tiene sentido hablar de energía absoluta, pero sí de diferencias de energía. La energía del vacío cuando se define escoge un origen canónico. $\mathbb {R}$
El espacio físico suele modelarse como un espacio afín en entornos no relativistas y en entornos relativistas. Para distinguirlos del espacio vectorial, a veces se los denomina espacios euclidianos y . $\mathbb {R} ^{3}$ $\mathbb {R} ^{1,3}$ ${\text{E}}(3)$ ${\text{E}}(1,3)$
Cualquier clase lateral de un subespacio $V$ de un espacio vectorial es un espacio afín sobre ese subespacio.
En particular, una línea en el plano que no pasa por el origen es un espacio afín que no es un espacio vectorial en relación con las operaciones que hereda de , aunque se le puede dar una estructura de espacio vectorial canónico eligiendo el punto más cercano al origen como el vector cero; de manera similar en dimensiones superiores y para cualquier espacio vectorial normado $\mathbb {R} ^{2}$
Si $T$ es una matriz y $b$ se encuentra en su espacio columna , el conjunto de soluciones de la ecuación $T x = b$ es un espacio afín sobre el subespacio de soluciones de $T x = 0$ .
Las soluciones de una ecuación diferencial lineal no homogénea forman un espacio afín sobre las soluciones de la ecuación lineal homogénea correspondiente.
Generalizando todo lo anterior, si $T : V \to W$ es una función lineal e $y$ se encuentra en su imagen , el conjunto de soluciones $x \in V$ de la ecuación $T x = y$ es un coconjunto del núcleo de $T$ , y por lo tanto es un espacio afín sobre $Ker T$ .
El espacio de subespacios complementarios (lineales) de un subespacio vectorial $V$ en un espacio vectorial $W$ es un espacio afín, sobre $Hom(W / V, V)$ . Es decir, si $0 \to V \to W \to X \to 0$ es una secuencia corta y exacta de espacios vectoriales, entonces el espacio de todas las descomposiciones de la secuencia exacta lleva naturalmente la estructura de un espacio afín sobre $Hom(X, V)$ .
El espacio de conexiones (visto desde el fibrado vectorial , donde es una variedad suave ) es un espacio afín para el espacio vectorial de 1-formas valoradas . El espacio de conexiones (visto desde el fibrado principal ) es un espacio afín para el espacio vectorial de 1-formas valoradas , donde es el fibrado adjunto asociado . $E\xrightarrow {\pi } M$ $M$ ${\text{End}}(E)$ $P\xrightarrow {\pi } M$ ${\text{ad}}(P)$ ${\text{ad}}(P)$

Bases y espacios afines

Para cualquier subconjunto no vacío $X$ de un espacio afín $A$ , existe un subespacio afín más pequeño que lo contiene, llamado espacio afín de $X$ . Es la intersección de todos los subespacios afines que contienen $a X$ , y su dirección es la intersección de las direcciones de los subespacios afines que contienen $a X$ .

El espacio afín de $X$ es el conjunto de todas las combinaciones afines (finitas) de puntos de $X$ , y su dirección es el espacio lineal de $x - y$ para $x$ e $y$ en $X$ . Si uno elige un punto particular $x 0$ , la dirección del espacio afín de $X$ es también el espacio lineal de $x - x 0$ para $x$ en $X$ .

Se dice también que el lapso afín de $X$ es generado por $X$ y que $X$ es un conjunto generador de su lapso afín.

Se dice que un conjunto $X$ de puntos de un espacio afín esafínmente independiente o, simplemente,independiente, si el espacio afín de cualquiersubconjunto estrictode $X$ es un subconjunto estricto del espacio afín de $X.$ UnLa base afín omarco baricéntrico(ver § Coordenadas baricéntricas, más abajo) de un espacio afín es un conjunto generador que también es independiente (es decir, unconjunto generador mínimo).

Recordemos que la dimensión de un espacio afín es la dimensión de su espacio vectorial asociado. Las bases de un espacio afín de dimensión finita $n$ son los subconjuntos independientes de $n + 1$ elementos o, equivalentemente, los subconjuntos generadores de $n + 1$ elementos. De manera equivalente, ${x 0, ..., x n$ } es una base afín de un espacio afín si y solo si ${x 1 - x 0, ..., x n - x 0$ } es una base lineal del espacio vectorial asociado.

Coordenadas

Hay dos tipos de sistemas de coordenadas fuertemente relacionados que pueden definirse en espacios afines.

Coordenadas baricéntricas

Sea $A$ un espacio afín de dimensión $n$ sobre un cuerpo $k$ , y sea una base afín de $A$ . Las propiedades de una base afín implican que para cada $x$ en $A$ existe una única $($ $n$ $+ 1)$ - tupla de elementos de $k$ tal que $\{x_{0},\dots ,x_{n}\}$ $(\lambda _{0},\dots ,\lambda _{n})$

\lambda _{0}+\dots +\lambda _{n}=1

x=\lambda _{0}x_{0}+\dots +\lambda _{n}x_{n}.

Las coordenadas baricéntricas de $x$ sobre la base afín se denominan coordenadas baricéntricas . Si las $x$ $i$ se consideran cuerpos que tienen pesos (o masas) , el punto $x$ es, por lo tanto, el baricentro de las $x$ $i$ , y esto explica el origen del término coordenadas baricéntricas . $\lambda _{i}$ $\{x_{0},\dots ,x_{n}\}$ $\lambda _{i}$

Las coordenadas baricéntricas definen un isomorfismo afín entre el espacio afín $A$ y el subespacio afín de $k n + 1$ definido por la ecuación . $\lambda _{0}+\dots +\lambda _{n}=1$

Para espacios afines de dimensión infinita, se aplica la misma definición, utilizando únicamente sumas finitas. Esto significa que para cada punto, solo un número finito de coordenadas son distintas de cero.

Coordenadas afines

Un marco afín de un espacio afín consta de un punto, llamado origen , y una base lineal del espacio vectorial asociado. Más precisamente, para un espacio afín $A$ con espacio vectorial asociado , el origen $o$ pertenece a $A$ , y la base lineal es una base $($ $v$ $1$ $, ...,$ $v$ $n$ $)$ de (para simplificar la notación, consideramos solo el caso de dimensión finita, el caso general es similar). ${\overrightarrow {A}}$ ${\overrightarrow {A}}$

Para cada punto $p$ de $A$ , existe una secuencia única de elementos del campo fundamental tal que $\lambda _{1},\dots ,\lambda _{n}$

p=o+\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n},

o equivalentemente

{\overrightarrow {op}}=\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n}.

Se denominan coordenadas afines de $p$ sobre el marco afín $($ $o$ $,$ $v$ $1$ $, ...,$ $v$ $n$ $)$ . $\lambda _{i}$

Ejemplo: En geometría euclidiana , las coordenadas cartesianas son coordenadas afines relativas a un marco ortonormal , es decir, un marco afín $(o, v 1, ..., v n)$ tal que $(v 1, ..., v n)$ es una base ortonormal .

Relación entre coordenadas baricéntricas y afines

Las coordenadas baricéntricas y las coordenadas afines están fuertemente relacionadas y pueden considerarse equivalentes.

De hecho, dado un marco baricéntrico

(x_{0},\dots ,x_{n}),

Se deduce inmediatamente el marco afín

(x_{0},{\overrightarrow {x_{0}x_{1}}},\dots ,{\overrightarrow {x_{0}x_{n}}})=\left(x_{0},x_{1}-x_{0},\dots ,x_{n}-x_{0}\right),

y si

\left(\lambda _{0},\lambda _{1},\dots ,\lambda _{n}\right)

son las coordenadas baricéntricas de un punto sobre el marco baricéntrico, entonces las coordenadas afines del mismo punto sobre el marco afín son

\left(\lambda _{1},\dots ,\lambda _{n}\right).

Por el contrario, si

\left(o,v_{1},\dots ,v_{n}\right)

es un marco afín, entonces

\left(o,o+v_{1},\dots ,o+v_{n}\right)

es un marco baricéntrico. Si

\left(\lambda _{1},\dots ,\lambda _{n}\right)

son las coordenadas afines de un punto sobre el marco afín, entonces sus coordenadas baricéntricas sobre el marco baricéntrico son

\left(1-\lambda _{1}-\dots -\lambda _{n},\lambda _{1},\dots ,\lambda _{n}\right).

Por lo tanto, las coordenadas baricéntricas y afines son casi equivalentes. En la mayoría de las aplicaciones, se prefieren las coordenadas afines, ya que implican menos coordenadas independientes. Sin embargo, en las situaciones en las que los puntos importantes del problema estudiado son afínmente independientes, las coordenadas baricéntricas pueden conducir a un cálculo más simple, como en el siguiente ejemplo.

Ejemplo del triangulo

Los vértices de un triángulo no plano forman una base afín del plano euclidiano . Las coordenadas baricéntricas permiten caracterizar fácilmente los elementos del triángulo que no involucran ángulos ni distancias:

Los vértices son los puntos de coordenadas baricéntricas $(1, 0, 0)$ , $(0, 1, 0)$ y $(0, 0, 1)$ . Las líneas que sostienen las aristas son los puntos que tienen una coordenada cero. Las aristas mismas son los puntos que tienen una coordenada cero y dos coordenadas no negativas. El interior del triángulo son los puntos cuyas coordenadas son todas positivas. Las medianas son los puntos que tienen dos coordenadas iguales, y el baricentro es el punto de coordenadas $( .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠1/3⁠ , ⁠1/3⁠ , ⁠1/3⁠ )$ .

Cambio de coordenadas

Caso de coordenadas baricéntricas

Las coordenadas baricéntricas se cambian fácilmente de una base a otra. Sean y bases afines de $A$ . Para cada $x$ en $A$ hay alguna tupla para la cual $\{x_{0},\dots ,x_{n}\}$ $\{x'_{0},\dots ,x'_{n}\}$ $\{\lambda _{0},\dots ,\lambda _{n}\}$

x=\lambda _{0}x_{0}+\dots +\lambda _{n}x_{n}.

De manera similar, para cada uno de la primera base, ahora tenemos en la segunda base $x_{i}\in \{x_{0},\dots ,x_{n}\}$

x_{i}=\lambda _{i,0}x'_{0}+\dots +\lambda _{i,j}x'_{j}+\dots +\lambda _{i,n}x'_{n}

para alguna tupla . Ahora podemos reescribir nuestra expresión en la primera base como una en la segunda con $\{\lambda _{i,0},\dots ,\lambda _{i,n}\}$

\,x=\sum _{i=0}^{n}\lambda _{i}x_{i}=\sum _{i=0}^{n}\lambda _{i}\sum _{j=0}^{n}\lambda _{i,j}x'_{j}=\sum _{j=0}^{n}{\biggl (}\sum _{i=0}^{n}\lambda _{i}\lambda _{i,j}{\biggr )}x'_{j}\,,

dándonos coordenadas en la segunda base como la tupla . ${\textstyle {\bigl \{}\sum _{i}\lambda _{i}\lambda _{i,0},\,\dots ,\,{}}$ ${\textstyle \sum _{i}\lambda _{i}\lambda _{i,n}{\bigr \}}}$

Caso de coordenadas afines

Las coordenadas afines también se cambian fácilmente de una base a otra. Sean , y , sistemas afines de $A$ . Para cada punto $p$ de $A$ , existe una secuencia única de elementos del campo base tal que $o$ $\{v_{1},\dots ,v_{n}\}$ $o'$ $\{v'_{1},\dots ,v'_{n}\}$ $\lambda _{1},\dots ,\lambda _{n}$

p=o+\lambda _{1}v_{1}+\dots +\lambda _{n}v_{n},

and similarly, for every $v_{i}\in \{v_{1},\dots ,v_{n}\}$ from the first basis, we now have in the second basis

o=o'+\lambda _{o,1}v'_{1}+\dots +\lambda _{o,j}v'_{j}+\dots +\lambda _{o,n}v'_{n}\,

v_{i}=\lambda _{i,1}v'_{1}+\dots +\lambda _{i,j}v'_{j}+\dots +\lambda _{i,n}v'_{n}

for tuple $\{\lambda _{o,1},\dots ,\lambda _{o,n}\}$ and tuples $\{\lambda _{i,1},\dots ,\lambda _{i,n}\}$ . Now we can rewrite our expression in the first basis as one in the second with

{\begin{aligned}\,p&=o+\sum _{i=1}^{n}\lambda _{i}v_{i}={\biggl (}o'+\sum _{j=1}^{n}\lambda _{o,j}v'_{j}{\biggr )}+\sum _{i=1}^{n}\lambda _{i}\sum _{j=1}^{n}\lambda _{i,j}v'_{j}\\&=o'+\sum _{j=1}^{n}{\biggl (}\lambda _{o,j}+\sum _{i=1}^{n}\lambda _{i}\lambda _{i,j}{\biggr )}v'_{j}\,,\end{aligned}}

giving us coordinates in the second basis as the tuple ${\textstyle {\bigl \{}\lambda _{o,1}+\sum _{i}\lambda _{i}\lambda _{i,1},\,\dots ,\,{}}$ ${\textstyle \lambda _{o,n}+\sum _{i}\lambda _{i}\lambda _{i,n}{\bigr \}}}$ .

Properties of affine homomorphisms

Matrix representation

An affine transformation $T$ is executed on a projective space $\mathbb {P} ^{3}$ of $\mathbb {R} ^{3}$ , by a 4 by 4 matrix with a special^[8] fourth column:

$A={\begin{bmatrix}a_{11}&a_{12}&a_{13}&0\\a_{21}&a_{22}&a_{23}&0\\a_{31}&a_{32}&a_{33}&0\\a_{41}&a_{42}&a_{43}&1\end{bmatrix}}={\begin{bmatrix}T(1,0,0)&0\\T(0,1,0)&0\\T(0,0,1)&0\\T(0,0,0)&1\end{bmatrix}}$

The transformation is affine instead of linear due to the inclusion of point $(0,0,0)$ , the transformed output of which reveals the affine shift.

Image and fibers

Let

f\colon E\to F

be an affine homomorphism, with

{\overrightarrow {f}}\colon {\overrightarrow {E}}\to {\overrightarrow {F}}

its associated linear map. The image of $f$ is the affine subspace $f(E)=\{f(a)\mid a\in E\}$ of $F$ , which has ${\overrightarrow {f}}({\overrightarrow {E}})$ as associated vector space. As an affine space does not have a zero element, an affine homomorphism does not have a kernel. However, the linear map ${\overrightarrow {f}}$ does, and if we denote by $K=\{v\in {\overrightarrow {E}}\mid {\overrightarrow {f}}(v)=0\}$ its kernel, then for any point $x$ of $f(E)$ , the inverse image $f^{-1}(x)$ of $x$ is an affine subspace of $E$ whose direction is $K$ . This affine subspace is called the fiber of $x$ .

Projection

An important example is the projection parallel to some direction onto an affine subspace. The importance of this example lies in the fact that Euclidean spaces are affine spaces, and that these kinds of projections are fundamental in Euclidean geometry.

More precisely, given an affine space $E$ with associated vector space ${\overrightarrow {E}}$ , let $F$ be an affine subspace of direction ${\overrightarrow {F}}$ , and $D$ be a complementary subspace of ${\overrightarrow {F}}$ in ${\overrightarrow {E}}$ (this means that every vector of ${\overrightarrow {E}}$ may be decomposed in a unique way as the sum of an element of ${\overrightarrow {F}}$ and an element of $D$ ). For every point $x$ of $E$ , its projection to $F$ parallel to $D$ is the unique point $p (x)$ in $F$ such that

p(x)-x\in D.

This is an affine homomorphism whose associated linear map ${\overrightarrow {p}}$ is defined by

{\overrightarrow {p}}(x-y)=p(x)-p(y),

for $x$ and $y$ in $E$ .

The image of this projection is $F$ , and its fibers are the subspaces of direction $D$ .

Quotient space

Although kernels are not defined for affine spaces, quotient spaces are defined. This results from the fact that "belonging to the same fiber of an affine homomorphism" is an equivalence relation.

Let $E$ be an affine space, and $D$ be a linear subspace of the associated vector space ${\overrightarrow {E}}$ . The quotient $E / D$ of $E$ by $D$ is the quotient of $E$ by the equivalence relation such that $x$ and $y$ are equivalent if

x-y\in D.

This quotient is an affine space, which has ${\overrightarrow {E}}/D$ as associated vector space.

For every affine homomorphism $E\to F$ , the image is isomorphic to the quotient of $E$ by the kernel of the associated linear map. This is the first isomorphism theorem for affine spaces.

Axioms

Affine spaces are usually studied by analytic geometry using coordinates, or equivalently vector spaces. They can also be studied as synthetic geometry by writing down axioms, though this approach is much less common. There are several different systems of axioms for affine space.

Coxeter (1969, p. 192) axiomatizes the special case of affine geometry over the reals as ordered geometry together with an affine form of Desargues's theorem and an axiom stating that in a plane there is at most one line through a given point not meeting a given line.

Affine planes satisfy the following axioms (Cameron 1991, chapter 2): (in which two lines are called parallel if they are equal or disjoint):

Any two distinct points lie on a unique line.
Given a point and line there is a unique line that contains the point and is parallel to the line
There exist three non-collinear points.

As well as affine planes over fields (or division rings), there are also many non-Desarguesian planes satisfying these axioms. (Cameron 1991, chapter 3) gives axioms for higher-dimensional affine spaces.

Purely axiomatic affine geometry is more general than affine spaces and is treated in a separate article.

Relation to projective spaces

Affine spaces are contained in projective spaces. For example, an affine plane can be obtained from any projective plane by removing one line and all the points on it, and conversely any affine plane can be used to construct a projective plane as a closure by adding a line at infinity whose points correspond to equivalence classes of parallel lines. Similar constructions hold in higher dimensions.

Further, transformations of projective space that preserve affine space (equivalently, that leave the hyperplane at infinity invariant as a set) yield transformations of affine space. Conversely, any affine linear transformation extends uniquely to a projective linear transformation, so the affine group is a subgroup of the projective group. For instance, Möbius transformations (transformations of the complex projective line, or Riemann sphere) are affine (transformations of the complex plane) if and only if they fix the point at infinity.

Affine algebraic geometry

In algebraic geometry, an affine variety (or, more generally, an affine algebraic set) is defined as the subset of an affine space that is the set of the common zeros of a set of so-called polynomial functions over the affine space. For defining a polynomial function over the affine space, one has to choose an affine frame. Then, a polynomial function is a function such that the image of any point is the value of some multivariate polynomial function of the coordinates of the point. As a change of affine coordinates may be expressed by linear functions (more precisely affine functions) of the coordinates, this definition is independent of a particular choice of coordinates.

The choice of a system of affine coordinates for an affine space $\mathbb {A} _{k}^{n}$ of dimension $n$ over a field $k$ induces an affine isomorphism between $\mathbb {A} _{k}^{n}$ and the affine coordinate space $k n$ . This explains why, for simplification, many textbooks write $\mathbb {A} _{k}^{n}=k^{n}$ , and introduce affine algebraic varieties as the common zeros of polynomial functions over $k n$ .^[9]

As the whole affine space is the set of the common zeros of the zero polynomial, affine spaces are affine algebraic varieties.

Ring of polynomial functions

By the definition above, the choice of an affine frame of an affine space $\mathbb {A} _{k}^{n}$ allows one to identify the polynomial functions on $\mathbb {A} _{k}^{n}$ with polynomials in $n$ variables, the ith variable representing the function that maps a point to its $i$ th coordinate. It follows that the set of polynomial functions over $\mathbb {A} _{k}^{n}$ is a $k$ -algebra, denoted $k\left[\mathbb {A} _{k}^{n}\right]$ , which is isomorphic to the polynomial ring $k\left[X_{1},\dots ,X_{n}\right]$ .

When one changes coordinates, the isomorphism between $k\left[\mathbb {A} _{k}^{n}\right]$ and $k[X_{1},\dots ,X_{n}]$ changes accordingly, and this induces an automorphism of $k\left[X_{1},\dots ,X_{n}\right]$ , which maps each indeterminate to a polynomial of degree one. It follows that the total degree defines a filtration of $k\left[\mathbb {A} _{k}^{n}\right]$ , which is independent from the choice of coordinates. The total degree defines also a graduation, but it depends on the choice of coordinates, as a change of affine coordinates may map indeterminates on non-homogeneous polynomials.

Zariski topology

Affine spaces over topological fields, such as the real or the complex numbers, have a natural topology. The Zariski topology, which is defined for affine spaces over any field, allows use of topological methods in any case. Zariski topology is the unique topology on an affine space whose closed sets are affine algebraic sets (that is sets of the common zeros of polynomial functions over the affine set). As, over a topological field, polynomial functions are continuous, every Zariski closed set is closed for the usual topology, if any. In other words, over a topological field, Zariski topology is coarser than the natural topology.

There is a natural injective function from an affine space into the set of prime ideals (that is the spectrum) of its ring of polynomial functions. When affine coordinates have been chosen, this function maps the point of coordinates $\left(a_{1},\dots ,a_{n}\right)$ to the maximal ideal $\left\langle X_{1}-a_{1},\dots ,X_{n}-a_{n}\right\rangle$ . This function is a homeomorphism (for the Zariski topology of the affine space and of the spectrum of the ring of polynomial functions) of the affine space onto the image of the function.

The case of an algebraically closed ground field is especially important in algebraic geometry, because, in this case, the homeomorphism above is a map between the affine space and the set of all maximal ideals of the ring of functions (this is Hilbert's Nullstellensatz).

This is the starting idea of scheme theory of Grothendieck, which consists, for studying algebraic varieties, of considering as "points", not only the points of the affine space, but also all the prime ideals of the spectrum. This allows gluing together algebraic varieties in a similar way as, for manifolds, charts are glued together for building a manifold.

Cohomology

Like all affine varieties, local data on an affine space can always be patched together globally: the cohomology of affine space is trivial. More precisely, $H^{i}\left(\mathbb {A} _{k}^{n},\mathbf {F} \right)=0$ for all coherent sheaves F, and integers $i>0$ . This property is also enjoyed by all other affine varieties. But also all of the étale cohomology groups on affine space are trivial. In particular, every line bundle is trivial. More generally, the Quillen–Suslin theorem implies that every algebraic vector bundle over an affine space is trivial.

Notes

^ The word translation is generally preferred to displacement vector, which may be confusing, as displacements include also rotations.
^ Berger 1987, p. 32
^ Berger, Marcel (1984), "Affine spaces", Problems in Geometry, Springer, p. 11, ISBN 9780387909714
^ Berger 1987, p. 33
^ Snapper, Ernst; Troyer, Robert J. (1989), Metric Affine Geometry, p. 6
^ Tarrida, Agusti R. (2011), "Affine spaces", Affine Maps, Euclidean Motions and Quadrics, Springer, pp. 1–2, ISBN 9780857297105
^ Nomizu & Sasaki 1994, p. 7
^ Strang, Gilbert (2009). Introduction to Linear Algebra (4th ed.). Wellesley: Wellesley-Cambridge Press. p. 460. ISBN 978-0-9802327-1-4.{{cite book}}: CS1 maint: date and year (link)
^ Hartshorne 1977, Ch. I, § 1.

References

Berger, Marcel (1984), "Espacios afines", Problemas de geometría , Springer-Verlag, ISBN 978-0-387-90971-4
Berger, Marcel (1987), Geometría I , Berlín: Springer, ISBN 3-540-11658-3
Cameron, Peter J. (1991), Espacios proyectivos y polares, QMW Maths Notes, vol. 13, Londres: Queen Mary and Westfield College School of Mathematical Sciences, MR 1153019
Coxeter, Harold Scott MacDonald (1969), Introducción a la geometría (2.ª ed.), Nueva York: John Wiley & Sons , ISBN 978-0-471-50458-0, Sr. 0123930
Dolgachev, IV ; Shirokov, AP (2001) [1994], "Espacio afín", Enciclopedia de Matemáticas , EMS Press
Hartshorne, Robin (1977). Geometría algebraica . Springer-Verlag . ISBN. 978-0-387-90244-9.Zbl 0367.14001 .
Nomizu, K. ; Sasaki, S. (1994), Geometría diferencial afín (Nueva ed.), Cambridge University Press, ISBN 978-0-521-44177-3
Snapper, Ernst ; Troyer, Robert J. (1989), Metric Affine Geometry (edición Dover, publicada por primera vez en la edición de 1989), Dover Publications, ISBN 0-486-66108-3
Reventós Tarrida, Agustí (2011), "Espacios afines", Mapas afines, movimientos euclidianos y cuádricas, Springer, ISBN 978-0-85729-709-9