
En geometría , un objeto tiene simetría si hay una operación o transformación (como traslación , escala , rotación o reflexión ) que asigna la figura/objeto a sí mismo (es decir, el objeto tiene una invariancia bajo la transformación). [1] Por lo tanto, una simetría puede considerarse como una inmunidad al cambio. [2] Por ejemplo, un círculo girado alrededor de su centro tendrá la misma forma y tamaño que el círculo original, ya que todos los puntos antes y después de la transformación serían indistinguibles. Por tanto, se dice que un círculo es simétrico bajo rotación o que tiene simetría rotacional . Si la isometría es la reflexión de una figura plana respecto de una recta, entonces se dice que la figura tiene simetría reflexiva o simetría lineal ; [3] también es posible que una figura/objeto tenga más de un eje de simetría. [4]
Los tipos de simetrías posibles para un objeto geométrico dependen del conjunto de transformaciones geométricas disponibles y de qué propiedades del objeto deben permanecer sin cambios después de una transformación. Debido a que la composición de dos transformadas también es una transformación y cada transformación tiene, por definición, una transformación inversa que la deshace, el conjunto de transformaciones bajo las cuales un objeto es simétrico forman un grupo matemático , el grupo de simetría del objeto. [5]
El grupo más común de transformaciones aplicadas a objetos se denomina grupo euclidiano de " isometrías ", que son transformaciones que preservan la distancia en el espacio comúnmente denominado bidimensional o tridimensional (es decir, en espacios euclidianos de geometría plana o geometría sólida ). . Estas isometrías constan de reflexiones , rotaciones , traslaciones y combinaciones de estas operaciones básicas. [6] Bajo una transformación isométrica, se dice que un objeto geométrico es simétrico si, después de la transformación, el objeto es indistinguible del objeto antes de la transformación. [7] Un objeto geométrico suele ser simétrico sólo bajo un subconjunto o " subgrupo " de todas las isometrías. Los tipos de subgrupos de isometría se describen a continuación, seguidos de otros tipos de grupos de transformación y de los tipos de invariancia de objetos que son posibles en geometría.
Según el teorema de Cartan-Dieudonné , una transformación ortogonal en un espacio n -dimensional puede representarse mediante la composición de como máximo n reflexiones.
La simetría reflexiva, simetría lineal, simetría especular, simetría de imagen especular o simetría bilateral es simetría con respecto a la reflexión. [8]
En una dimensión hay un punto de simetría alrededor del cual tiene lugar la reflexión; en dos dimensiones, hay un eje de simetría (también conocido como eje de simetría), y en tres dimensiones hay un plano de simetría. [3] [9] Un objeto o figura para el cual cada punto tiene un mapeo uno a uno sobre otro, equidistante de y en lados opuestos de un plano común se llama espejo simétrico (para obtener más información, consulte imagen especular ).
El eje de simetría de una figura bidimensional es una línea tal que, si se construye una perpendicular , dos puntos cualesquiera que se encuentren en la perpendicular a distancias iguales del eje de simetría son idénticos. Otra forma de pensarlo es que si la forma se doblara por la mitad sobre el eje, las dos mitades serían idénticas como imágenes especulares entre sí. Por ejemplo. un cuadrado tiene cuatro ejes de simetría, porque hay cuatro formas diferentes de doblarlo y hacer que los bordes coincidan. Otro ejemplo sería el de un círculo , que por el mismo motivo pasa por su centro una infinidad de ejes de simetría. [10]
Si la letra T se refleja a lo largo de un eje vertical, parece igual. A esto a veces se le llama simetría vertical. Por tanto, se puede describir este fenómeno sin ambigüedades diciendo que "T tiene un eje de simetría vertical" o que "T tiene simetría izquierda-derecha".
Los triángulos con simetría de reflexión son isósceles , los cuadriláteros con esta simetría son cometas y trapecios isósceles . [11]
Para cada línea o plano de reflexión, el grupo de simetría es isomorfo con C s (ver grupos de puntos en tres dimensiones para más), uno de los tres tipos de orden dos ( involuciones ), por lo tanto algebraicamente isomorfo a C 2 . El dominio fundamental es un semiplano o semiespacio . [12]

La simetría de reflexión se puede generalizar a otras isometrías del espacio m -dimensional que son involuciones , como
en un determinado sistema de coordenadas cartesianas . Esto refleja el espacio a lo largo de un subespacio afín ( m − k ) -dimensional . [13] Si k = m , entonces dicha transformación se conoce como reflexión puntual o inversión a través de un punto . En el plano ( m = 2), una reflexión puntual es lo mismo que una rotación de media vuelta (180°); vea abajo. La simetría antípoda es un nombre alternativo para una simetría de reflexión puntual a través del origen. [14]
Tal "reflexión" preserva la orientación si y sólo si k es un número par . [15] Esto implica que para m = 3 (así como para otros m impares ), una reflexión puntual cambia la orientación del espacio, como una simetría de imagen especular. Eso explica por qué en física el término P- simetría (P significa paridad ) se utiliza tanto para la reflexión puntual como para la simetría especular. Dado que una reflexión puntual en tres dimensiones cambia un sistema de coordenadas zurdos a un sistema de coordenadas diestros , la simetría bajo una reflexión puntual también se denomina simetría izquierda-derecha. [dieciséis]

La simetría rotacional es simetría con respecto a algunas o todas las rotaciones en el espacio euclidiano de m dimensiones. Las rotaciones son isometrías directas , que son isometrías que conservan la orientación . [17] Por lo tanto, un grupo de simetría de simetría rotacional es un subgrupo del grupo euclidiano especial E + ( m ) .
La simetría con respecto a todas las rotaciones sobre todos los puntos implica simetría traslacional con respecto a todas las traslaciones (porque las traslaciones son composiciones de rotaciones sobre distintos puntos), [18] y el grupo de simetría es el conjunto E + ( m ). Esto no se aplica a los objetos porque hace que el espacio sea homogéneo, pero puede aplicarse a las leyes físicas.
Para la simetría con respecto a rotaciones alrededor de un punto, se puede tomar ese punto como origen. Estas rotaciones forman el grupo ortogonal especial SO( m ), que puede representarse mediante el grupo de matrices ortogonales m × m con determinante 1. Para m = 3, este es el grupo de rotación SO(3) . [19]
Dicho de manera ligeramente diferente, el grupo de rotación de un objeto es el grupo de simetría dentro de E + ( m ), el grupo de movimientos rígidos; [20] es decir, la intersección del grupo de simetría completa y el grupo de movimientos rígidos. Para objetos quirales, es lo mismo que el grupo de simetría completo.
Las leyes de la física son invariantes SO(3) si no distinguen diferentes direcciones en el espacio. Debido al teorema de Noether , la simetría rotacional de un sistema físico es equivalente a la ley de conservación del momento angular . [21] Para obtener más información, consulte invariancia rotacional .

La simetría traslacional deja un objeto invariante bajo un grupo de traslaciones discreto o continuo . [22] La ilustración de la derecha muestra cuatro huellas congruentes generadas por traslaciones a lo largo de la flecha. Si la línea de huellas se extendiera hasta el infinito en ambas direcciones, entonces tendrían una simetría traslacional discreta; cualquier traducción que mapeara una huella sobre otra dejaría toda la línea sin cambios.

En 2D, una simetría de reflexión de planeo (también llamada simetría de plano de planeo en 3D y transflexión en general) significa que una reflexión en una línea o plano combinada con una traslación a lo largo de la línea o en el plano, da como resultado el mismo objeto ( como en el caso de las huellas). [2] [23] La composición de dos reflexiones de deslizamiento da como resultado una simetría de traslación con el doble del vector de traslación. El grupo de simetría que comprende reflexiones de deslizamiento y traslaciones asociadas es el grupo de friso p11g , y es isomorfo con el grupo cíclico infinito Z.
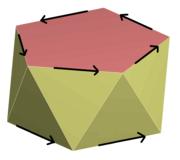
En 3D, una reflexión rotatoria , reflexión rotatoria o rotación impropia es una rotación alrededor de un eje combinada con una reflexión en un plano perpendicular a ese eje. [24] Los grupos de simetría asociados con las reflexiones del rotor incluyen:
Para más información, consulte grupos de puntos en tres dimensiones .
En geometría 3D y superiores, un eje de tornillo (o traslación giratoria) es una combinación de una rotación y una traslación a lo largo del eje de rotación. [25]
La simetría helicoidal es el tipo de simetría que se observa en objetos cotidianos como resortes , juguetes Slinky , brocas y barrenas . El concepto de simetría helicoidal se puede visualizar como el trazado en el espacio tridimensional que resulta de girar un objeto a una velocidad angular constante , mientras simultáneamente se traslada a una velocidad lineal constante a lo largo de su eje de rotación. En cualquier momento, estos dos movimientos se combinan para dar un ángulo de enrollamiento que ayuda a definir las propiedades de la hélice trazada. [26] Cuando el objeto de rastreo gira rápidamente y se traslada lentamente, el ángulo de enrollado será cercano a 0°. Por el contrario, si el objeto gira lentamente y se traslada rápidamente, el ángulo de enrollado se acercará a los 90°.

Se pueden distinguir tres clases principales de simetría helicoidal, basadas en la interacción del ángulo de enrollado y las simetrías de traslación a lo largo del eje:



En 4D, se puede generar una simetría de doble rotación como la combinación de dos rotaciones ortogonales. [29] Es similar al eje de tornillo 3D, que es la combinación de una rotación y una traslación ortogonal.
Una definición más amplia de simetría geométrica permite operaciones de un grupo más grande que el grupo euclidiano de isometrías. Ejemplos de grupos de simetría geométrica más grandes son:
En el programa Erlangen de Felix Klein , cada posible grupo de simetrías define una geometría en la que los objetos que están relacionados por un miembro del grupo de simetría se consideran equivalentes. [32] Por ejemplo, el grupo euclidiano define la geometría euclidiana , mientras que el grupo de transformaciones de Möbius define la geometría proyectiva .

La simetría de escala significa que si un objeto se expande o reduce de tamaño, el nuevo objeto tiene las mismas propiedades que el original. [33] Esta autosimilitud se observa en muchas estructuras naturales, como cúmulos, relámpagos, helechos y costas, en una amplia gama de escalas. Por lo general, no se encuentra en estructuras unidas gravitacionalmente, por ejemplo, en la forma de las patas de un elefante y un ratón (el llamado escalado alométrico ). De manera similar, si una vela de cera blanda se agrandara hasta el tamaño de un árbol alto, inmediatamente colapsaría bajo su propio peso.
Los fractales demuestran una forma más sutil de simetría de escala . Tal como los concibió Benoît Mandelbrot , los fractales son un concepto matemático en el que la estructura de una forma compleja parece similar en cualquier grado de ampliación , [34] bien visto en el conjunto de Mandelbrot . Una costa es un ejemplo de fractal natural, ya que conserva una complejidad aparentemente similar en todos los niveles, desde la vista de un satélite hasta un examen microscópico de cómo el agua choca contra los granos de arena individuales. Otro ejemplo es la ramificación de árboles, que permite que pequeñas ramitas sustituyan a árboles completos en los dioramas .
Debido a que los fractales pueden generar la apariencia de patrones en la naturaleza , tienen una belleza y una familiaridad que no suele verse en las funciones generadas matemáticamente. Los fractales también han encontrado un lugar en los efectos de películas generados por computadora , donde su capacidad para crear curvas complejas con simetrías fractales da como resultado mundos virtuales más realistas .
A cada geometría, Felix Klein asociaba un grupo subyacente de simetrías . La jerarquía de las geometrías se representa así matemáticamente como una jerarquía de estos grupos y una jerarquía de sus invariantes . Por ejemplo, las longitudes, los ángulos y las áreas se conservan con respecto al grupo de simetrías euclidianas , mientras que bajo las transformaciones proyectivas más generales sólo se conservan la estructura de incidencia y la razón cruzada . Un concepto de paralelismo , que se conserva en la geometría afín , no tiene significado en la geometría proyectiva . Luego, al abstraer los grupos de simetrías subyacentes de las geometrías, las relaciones entre ellos pueden restablecerse a nivel de grupo. Dado que el grupo de geometría afín es un subgrupo del grupo de geometría proyectiva, cualquier noción invariante en geometría proyectiva es a priori significativa en geometría afín; pero no al revés. Si agrega las simetrías requeridas, tendrá una teoría más poderosa pero menos conceptos y teoremas (que serán más profundos y más generales).
William Thurston introdujo una versión similar de las simetrías en geometría. Una geometría modelo es una variedad lisa X simplemente conectada junto con una acción transitiva de un grupo de Lie G sobre X con estabilizadores compactos. El grupo de Lie puede considerarse como el grupo de simetrías de la geometría.
Un modelo de geometría se llama maximal si G es máximo entre grupos que actúan suave y transitivamente sobre X con estabilizadores compactos, es decir, si es el grupo máximo de simetrías. A veces esta condición se incluye en la definición de una geometría modelo.
Una estructura geométrica en una variedad M es un difeomorfismo de M a X /Γ para algún modelo de geometría X , donde Γ es un subgrupo discreto de G que actúa libremente sobre X. Si una variedad dada admite una estructura geométrica, entonces admite una cuyo modelo es maximal.
Un modelo de geometría tridimensional X es relevante para la conjetura de geometrización si es máximo y si hay al menos una variedad compacta con una estructura geométrica modelada en X. Thurston clasificó las 8 geometrías del modelo que satisfacían estas condiciones; se enumeran a continuación y a veces se les llama geometrías de Thurston . (También hay innumerables geometrías de modelos sin cocientes compactos).