Geodésicas sobre un elipsoide

Caminos más cortos en una superficie cuadrática acotada, deformada y con forma de esfera

Una geodésica sobre un elipsoide achatado

El estudio de las geodésicas sobre un elipsoide surgió en conexión con la geodesia, específicamente con la solución de redes de triangulación . La figura de la Tierra se aproxima bien mediante un elipsoide achatado , una esfera ligeramente aplanada. Una geodésica es el camino más corto entre dos puntos sobre una superficie curva, análoga a una línea recta sobre una superficie plana. La solución de una red de triangulación sobre un elipsoide es, por tanto, un conjunto de ejercicios de trigonometría esferoidal (Euler 1755).

Si se considera la Tierra como una esfera , las geodésicas son círculos máximos (todos ellos cerrados) y los problemas se reducen a los de la trigonometría esférica . Sin embargo, Newton (1687) demostró que el efecto de la rotación de la Tierra hace que se parezca a un elipsoide ligeramente achatado: en este caso, el ecuador y los meridianos son las únicas geodésicas cerradas simples. Además, el camino más corto entre dos puntos del ecuador no necesariamente discurre a lo largo del ecuador. Finalmente, si el elipsoide se perturba aún más para convertirse en un elipsoide triaxial (con tres semiejes distintos), solo tres geodésicas son cerradas.

Geodésicas sobre un elipsoide de revolución

Existen varias formas de definir las geodésicas (Hilbert y Cohn-Vossen 1952, pp. 220-221). Una definición sencilla es la de la ruta más corta entre dos puntos de una superficie. Sin embargo, con frecuencia resulta más útil definirlas como rutas con curvatura geodésica cero , es decir, el análogo de las líneas rectas en una superficie curva. Esta definición abarca las geodésicas que recorren una distancia tan grande a través de la superficie del elipsoide que comienzan a regresar hacia el punto de partida, de modo que otras rutas son más directas, e incluye rutas que se cruzan o se vuelven a trazar. Los segmentos suficientemente cortos de una geodésica siguen siendo la ruta más corta entre sus puntos finales, pero las geodésicas no son necesariamente globalmente mínimas (es decir, las más cortas entre todas las rutas posibles). Toda ruta globalmente más corta es una geodésica, pero no al revés.

A finales del siglo XVIII, un elipsoide de revolución (también se utiliza el término esferoide ) era una aproximación bien aceptada a la figura de la Tierra . El ajuste de las redes de triangulación supuso reducir todas las mediciones a un elipsoide de referencia y resolver el problema bidimensional resultante como un ejercicio de trigonometría esferoidal (Bomford 1952, cap. 3) (Leick et al. 2015, §4.5).

Fig. 1. Geodésica AB sobre un elipsoide de revolución. N es el polo norte y EFH se encuentra sobre el ecuador.

Es posible reducir los diversos problemas geodésicos a uno de dos tipos. Considérense dos puntos: A en latitud φ ₁ y longitud λ ₁ y B en latitud φ ₂ y longitud λ ₂ (véase la figura 1). La geodésica de conexión (de A a B ) es AB , de longitud s ₁₂ , que tiene acimutes α ₁ y α ₂ en los dos puntos finales. ^[1] Los dos problemas geodésicos que se consideran habitualmente son:

1. el problema geodésico directo o primer problema geodésico , dados A , α ₁ y s ₁₂ , determine B y α ₂ ;
2. El problema geodésico inverso o segundo problema geodésico , dados A y B , determina s ₁₂ , α ₁ y α ₂ .

Como se puede ver en la figura 1, estos problemas implican la solución del triángulo NAB dado un ángulo, α ₁ para el problema directo y λ ₁₂ = λ ₂ − λ ₁ para el problema inverso, y sus dos lados adyacentes. Para una esfera, las soluciones a estos problemas son ejercicios simples de trigonometría esférica , cuya solución se da mediante fórmulas para resolver un triángulo esférico . (Véase el artículo sobre navegación en círculo máximo ).

Para un elipsoide de revolución, la constante característica que define la geodésica fue hallada por Clairaut (1735). Legendre (1806) y Oriani (1806) (y artículos posteriores de 1808 y 1810) dieron una solución sistemática para las trayectorias de las geodésicas. Bessel (1825) dio la solución completa para el problema directo (con tablas de cálculo y un ejemplo resuelto).

Durante el siglo XVIII, las geodésicas se denominaban normalmente "líneas más cortas". El término "línea geodésica" (en realidad, una curva ) fue acuñado por Laplace (1799b):

Nous désignerons cette ligne sous le nom de ligne géodésique [Llamaremos a esta línea línea geodésica ].

Esta terminología se introdujo en inglés como "línea geodésica" o como "línea geodésica", por ejemplo (Hutton 1811, p. 115),

Una línea trazada en la forma que hemos estado describiendo, o deducida a partir de medidas trigonométricas, por los medios que hemos indicado, se llama línea geodésica o geodésica: tiene la propiedad de ser la más corta que puede trazarse entre sus dos extremos en la superficie de la Tierra; y es, por lo tanto, la medida de itinerario adecuada de la distancia entre esos dos puntos.

En su adopción en otros campos se prefirió la línea geodésica , frecuentemente abreviada como geodésica .

En esta sección se aborda el problema de un elipsoide de revolución (tanto achatado como prolato). El problema de un elipsoide triaxial se aborda en la siguiente sección.

Ecuaciones para una geodésica

En este trabajo se desarrollan las ecuaciones para una geodésica; la derivación sigue de cerca la de Bessel (1825). Jordan y Eggert (1941), Bagratuni (1962, §15), Gan'shin (1967, cap. 5), Krakiwsky y Thomson (1974, §4), Rapp (1993, §1.2), Jekeli (2012) y Borre y Strang (2012) también proporcionan derivaciones de estas ecuaciones.

Consideremos un elipsoide de revolución con radio ecuatorial a y semieje polar b . Definamos el aplanamiento f , la excentricidad e y la segunda excentricidad e ′ :

${\displaystyle f={\frac {a-b}{a}},\quad e={\frac {\sqrt {a^{2}-b^{2}}}{a}}={\sqrt {f(2-f)}},\quad e'={\frac {\sqrt {a^{2}-b^{2}}}{b}}={\frac {e}{1-f}}.}$

(En la mayoría de las aplicaciones en geodesia, se considera que el elipsoide es achatado, a > b ; sin embargo, la teoría se aplica sin cambios a los elipsoides alargados, a < b , en cuyo caso f , e ² y e ′ ² son negativos).

Sea un segmento elemental de una trayectoria en el elipsoide de longitud ds . De las figuras 2 y 3, vemos que si su acimut es α , entonces ds está relacionado con dφ y dλ por

${\displaystyle \cos \alpha \,ds=\rho \,d\varphi =-{\frac {dR}{\sin \varphi }},\quad \sin \alpha \,ds=R\,d\lambda ,}$ (1)

donde ρ es el radio de curvatura meridional , R = ν cos φ es el radio del círculo de latitud φ y ν es el radio de curvatura normal . Por lo tanto, el segmento elemental viene dado por

${\displaystyle ds^{2}=\rho ^{2}\,d\varphi ^{2}+R^{2}\,d\lambda ^{2}}$

o

${\displaystyle {\begin{aligned}ds&={\sqrt {\rho ^{2}\varphi '^{2}+R^{2}}}\,d\lambda \\&\equiv L(\varphi ,\varphi ')\,d\lambda ,\end{aligned}}}$

donde φ ′ = dφ / dλ y la función lagrangiana L depende de φ a través de ρ( φ ) y R ( φ ) . La longitud de un camino arbitrario entre ( φ ₁ , λ ₁ ) y ( φ ₂ , λ ₂ ) está dada por

${\displaystyle s_{12}=\int _{\lambda _{1}}^{\lambda _{2}}L(\varphi ,\varphi ')\,d\lambda ,}$

donde φ es una función de λ que satisface φ ( λ ₁ ) = φ ₁ y φ ( λ ₂ ) = φ ₂ . El camino más corto o geodésico implica encontrar la función φ ( λ ) que minimiza s ₁₂ . Este es un ejercicio de cálculo de variaciones y la condición de minimización está dada por la identidad de Beltrami ,

${\displaystyle L-\varphi '{\frac {\partial L}{\partial \varphi '}}={\text{const.}}}$

Sustituyendo L y utilizando las ecuaciones (1) se obtiene

${\displaystyle R\sin \alpha ={\text{const.}}}$

Clairaut (1735) encontró esta relación , utilizando una construcción geométrica; Lyusternik (1964, §10) presenta una derivación similar. ^[2] La diferenciación de esta relación da

${\displaystyle d\alpha =\sin \varphi \,d\lambda .}$

Esto, junto con las ecuaciones (1) , conduce a un sistema de ecuaciones diferenciales ordinarias para una geodésica.

${\displaystyle {\frac {d\varphi }{ds}}={\frac {\cos \alpha }{\rho }};\quad {\frac {d\lambda }{ds}}={\frac {\sin \alpha }{\nu \cos \varphi }};\quad {\frac {d\alpha }{ds}}={\frac {\tan \varphi \sin \alpha }{\nu }}.}$

Podemos expresar R en términos de la latitud paramétrica , β , usando

${\displaystyle R=a\cos \beta ,}$

Y la relación de Clairaut se convierte entonces en

${\displaystyle \sin \alpha _{1}\cos \beta _{1}=\sin \alpha _{2}\cos \beta _{2}.}$

Esta es la regla del seno de la trigonometría esférica que relaciona dos lados del triángulo NAB (ver Fig. 4), NA = 1 ⁄ 2 π − β ₁ , y NB = 1 ⁄ 2 π − β ₂ y sus ángulos opuestos B = π − α ₂ y A = α ₁ .

Para hallar la relación para el tercer lado AB = σ ₁₂ , la longitud del arco esférico , y el ángulo incluido N = ω ₁₂ , la longitud esférica , es útil considerar el triángulo NEP que representa una geodésica que comienza en el ecuador; véase la figura 5. En esta figura, las variables referidas a la esfera auxiliar se muestran con las cantidades correspondientes para el elipsoide que se muestran entre paréntesis. Las cantidades sin subíndices se refieren al punto arbitrario P ; E , el punto en el que la geodésica cruza el ecuador en dirección norte, se utiliza como origen para σ , s y ω .

Fig. 6. Elemento diferencial de una geodésica sobre una esfera.

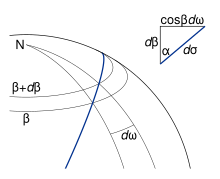
Si el lado EP se extiende moviendo P infinitesimalmente (ver Fig. 6), obtenemos

${\displaystyle \cos \alpha \,d\sigma =d\beta ,\quad \sin \alpha \,d\sigma =\cos \beta \,d\omega .}$ (2)

Combinando las ecuaciones (1) y (2) se obtienen ecuaciones diferenciales para s y λ

${\displaystyle {\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\frac {\sin \beta }{\sin \varphi }}.}$

La relación entre β y φ es

${\displaystyle \tan \beta ={\sqrt {1-e^{2}}}\tan \varphi =(1-f)\tan \varphi ,}$

Lo cual da

${\displaystyle {\frac {\sin \beta }{\sin \varphi }}={\sqrt {1-e^{2}\cos ^{2}\beta }},}$

de modo que las ecuaciones diferenciales para la geodésica se convierten en

${\displaystyle {\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\sqrt {1-e^{2}\cos ^{2}\beta }}.}$

El último paso es utilizar σ como parámetro independiente en ambas ecuaciones diferenciales y, por lo tanto, expresar s y λ como integrales. Al aplicar la regla del seno a los vértices E y G en el triángulo esférico EGP de la figura 5, se obtiene

${\displaystyle \sin \beta =\sin \beta (\sigma ;\alpha _{0})=\cos \alpha _{0}\sin \sigma ,}$

donde α ₀ es el acimut en E . Sustituyendo esto en la ecuación para ds / d σ e integrando el resultado se obtiene

${\displaystyle {\frac {s}{b}}=\int _{0}^{\sigma }{\sqrt {1+k^{2}\sin ^{2}\sigma '}}\,d\sigma ',}$ (3)

dónde

${\displaystyle k=e'\cos \alpha _{0},}$

y los límites de la integral se eligen de modo que s ( σ = 0) = 0 . Legendre (1811, p. 180) señaló que la ecuación para s es la misma que la ecuación para el arco de una elipse con semiejes b √ 1 + e ′ ² cos ² α ₀ y b . Para expresar la ecuación para λ en términos de σ , escribimos

${\displaystyle d\omega ={\frac {\sin \alpha _{0}}{\cos ^{2}\beta }}\,d\sigma ,}$

que se desprende de la ecuación 2 y de la relación de Clairaut. Esto da como resultado

${\displaystyle \lambda -\lambda _{0}=\omega -f\sin \alpha _{0}\int _{0}^{\sigma }{\frac {2-f}{1+(1-f){\sqrt {1+k^{2}\sin ^{2}\sigma '}}}}\,d\sigma ',}$ (4)

y los límites de las integrales se eligen de modo que λ = λ ₀ en el cruce del ecuador, σ = 0 .

Con esto se completa la solución de la trayectoria de una geodésica utilizando la esfera auxiliar. Con este dispositivo se puede representar con exactitud un círculo máximo en una geodésica sobre un elipsoide de revolución.

También existen varias formas de aproximar las geodésicas en un elipsoide terrestre (con un pequeño aplanamiento) (Rapp 1991, §6); algunas de ellas se describen en el artículo sobre distancia geográfica . Sin embargo, suelen ser comparables en complejidad al método para la solución exacta (Jekeli 2012, §2.1.4).

Comportamiento de las geodésicas

Fig. 7. Los meridianos y el ecuador son las únicas geodésicas cerradas. (Para los elipsoides muy aplanados, existen otras geodésicas cerradas; véanse las Figs. 11 y 12).

Geodésica sobre un elipsoide oblato ( f = 1 ⁄ 50 ) con α ₀ =45° .

Fig. 10. Geodésica sobre un elipsoide alargado ( f = − 1 ⁄ 50 ) con α ₀ =45° . Comparar con la figura 8.

La figura 7 muestra las geodésicas cerradas simples que consisten en los meridianos (verde) y el ecuador (rojo). (Aquí, la calificación "simple" significa que la geodésica se cierra sobre sí misma sin una autointersección intermedia). Esto se desprende de las ecuaciones para las geodésicas dadas en la sección anterior.

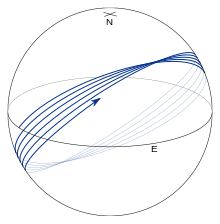
Todas las demás geodésicas están representadas por las figuras 8 y 9, que muestran una geodésica que comienza en el ecuador con α ₀ = 45° . La geodésica oscila alrededor del ecuador. Los cruces ecuatoriales se denominan nodos y los puntos de latitud máxima o mínima se denominan vértices ; las latitudes paramétricas de los vértices están dadas por β = ±( 1 ⁄ 2 π − |α ₀ |) . La geodésica completa una oscilación completa en latitud antes de que la longitud haya aumentado en360° . Por lo tanto, en cada cruce sucesivo hacia el norte del ecuador (ver Figura 8), λ no completa un circuito completo del ecuador en aproximadamente 2 π f senα ₀ (para un elipsoide alargado, esta cantidad es negativa y λ completa más que un circuito completo; ver Figura 10). Para casi todos los valores de α ₀ , la geodésica llenará esa porción del elipsoide entre las dos latitudes de los vértices (ver Figura 9).

Dos geodésicas cerradas adicionales para el elipsoide oblato, b ⁄ a = 2 ⁄ 7 .

Si el elipsoide es suficientemente achatado, es decir, b ⁄ a < 1 ⁄ 2 , es posible otra clase de geodésicas cerradas simples (Klingenberg 1982, §3.5.19). Dos de estas geodésicas se ilustran en las figuras 11 y 12. Aquí b ⁄ a = 2 ⁄ 7 y el acimut ecuatorial, α ₀ , para la geodésica verde (resp. azul) se elige como53,175° (respetuoso del medio ambiente)75,192° ), de modo que la geodésica completa 2 (resp. 3) oscilaciones completas alrededor del ecuador en un circuito del elipsoide.

Fig. 13. Geodésicas (azul) desde un único punto para f = 1 ⁄ 10 , φ ₁ =−30° ; los círculos geodésicos se muestran en verde y el lugar de corte en rojo.

La figura 13 muestra geodésicas (en azul) que emanan A con α ₁ un múltiplo de15° hasta el punto en que dejan de ser caminos más cortos. (El aplanamiento se ha aumentado a 1 ⁄ 10 para acentuar los efectos elipsoidales.) También se muestran (en verde) curvas de constante s ₁₂ , que son los círculos geodésicos centrados en A . Gauss (1828) demostró que, en cualquier superficie, las geodésicas y el círculo geodésico se cortan en ángulos rectos.

La línea roja es el lugar geométrico de corte , el lugar geométrico de los puntos que tienen múltiples (dos en este caso) geodésicas más cortas desde A. En una esfera, el lugar geométrico de corte es un punto. En un elipsoide achatado (mostrado aquí), es un segmento del círculo de latitud centrado en el punto antípoda a A , φ = − φ _1. La extensión longitudinal del lugar geométrico de corte es aproximadamente λ ₁₂ ∈ [ π (1 − f cos φ ₁ ), π (1 + f cos φ ₁ )] . Si A se encuentra en el ecuador, φ ₁ = 0 , esta relación es exacta y, como consecuencia, el ecuador solo es una geodésica más corta si | λ ₁₂ | ≤ π (1 − f ) . Para un elipsoide alargado, el lugar de corte es un segmento del antimeridiano centrado en el punto antípoda a A , λ ₁₂ = π , y esto significa que las geodésicas meridionales dejan de ser caminos más cortos antes de que se alcance el punto antípoda.

Propiedades diferenciales de las geodésicas

Varios problemas que involucran geodésicas requieren conocer su comportamiento cuando son perturbadas. Esto es útil en ajustes trigonométricos (Ehlert 1993), determinando las propiedades físicas de señales que siguen geodésicas, etc. Considérese una geodésica de referencia, parametrizada por s , y una segunda geodésica a una pequeña distancia t ( s ) de ella. Gauss (1828) demostró que t ( s ) obedece a la ecuación de Gauss-Jacobi .

${\displaystyle {\frac {d^{2}t(s)}{ds^{2}}}+K(s)t(s)=0,}$

Fig. 14. Definición de longitud reducida y escala geodésica.

donde K ( s ) es la curvatura gaussiana en s . Como ecuación diferencial lineal y homogénea de segundo orden, su solución puede expresarse como la suma de dos soluciones independientes

${\displaystyle t(s_{2})=Cm(s_{1},s_{2})+DM(s_{1},s_{2})}$

dónde

${\displaystyle {\begin{aligned}m(s_{1},s_{1})&=0,\quad \left.{\frac {dm(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=1,\\M(s_{1},s_{1})&=1,\quad \left.{\frac {dM(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=0.\end{aligned}}}$

La cantidad m ( s ₁ , s ₂ ) = m ₁₂ es la llamada longitud reducida , y M ( s ₁ , s ₂ ) = M ₁₂ es la escala geodésica . ^[3] Sus definiciones básicas se ilustran en la figura 14.

La curvatura gaussiana para un elipsoide de revolución es

${\displaystyle K={\frac {1}{\rho \nu }}={\frac {{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}{b^{2}}}={\frac {b^{2}}{a^{4}{\bigl (}1-e^{2}\cos ^{2}\beta {\bigr )}^{2}}}.}$

Helmert (1880, Ec. (6.5.1.)) resolvió la ecuación de Gauss-Jacobi para este caso permitiendo que m ₁₂ y M ₁₂ se expresen como integrales.

Como vemos en la Fig. 14 (subfigura superior), la separación de dos geodésicas que comienzan en el mismo punto con acimutes que difieren en d α ₁ es m ₁₂ d α ₁ . En una superficie cerrada como un elipsoide, m ₁₂ oscila alrededor de cero. El punto en el que m ₁₂ se vuelve cero es el punto conjugado al punto de partida. Para que una geodésica entre A y B , de longitud s ₁₂ , sea un camino más corto debe satisfacer la condición de Jacobi (Jacobi 1837) (Jacobi 1866, §6) (Forsyth 1927, §§26-27) (Bliss 1916), de que no hay ningún punto conjugado a A entre A y B . Si esta condición no se cumple, entonces hay un camino cercano (no necesariamente una geodésica) que es más corto. Por lo tanto, la condición de Jacobi es una propiedad local de la geodésica y es sólo una condición necesaria para que la geodésica sea un camino más corto global. Las condiciones necesarias y suficientes para que una geodésica sea el camino más corto son:

• para un elipsoide achatado, | σ12 |_​ ≤π ;​
• para un elipsoide alargado, | λ12 |_​ ≤ π , si α ₀ ≠ 0 ; si α ₀ = 0 , se requiere la condición suplementaria m ₁₂ ≥ 0 si | λ12 |_​ = π .

Envolvente de geodésicas

Geodésicas desde un único punto ( f = 1 ⁄ 10 , φ ₁ =−30° )

Las geodésicas desde un punto particular A , si continúan más allá del lugar geométrico de corte, forman una envolvente ilustrada en la figura 15. Aquí, las geodésicas para las cuales α ₁ es un múltiplo de3° se muestran en azul claro. (Las geodésicas solo se muestran para su primer paso cerca del punto antípoda, no para los subsiguientes). Algunos círculos geodésicos se muestran en verde; estos forman cúspides en la envolvente. El lugar geométrico de corte se muestra en rojo. La envolvente es el lugar geométrico de los puntos que son conjugados a A ; los puntos de la envolvente se pueden calcular encontrando el punto en el que m ₁₂ = 0 en una geodésica. Jacobi (1891) llama a esta figura similar a una estrella producida por la envolvente un astroide .

Fuera de la astroide, dos geodésicas se intersecan en cada punto; por lo tanto, hay dos geodésicas (con una longitud de aproximadamente la mitad de la circunferencia del elipsoide) entre A y estos puntos. Esto corresponde a la situación en la esfera donde hay rutas "cortas" y "largas" en un gran círculo entre dos puntos. Dentro de la astroide, cuatro geodésicas se intersecan en cada punto. Cuatro de estas geodésicas se muestran en la Fig. 16 donde las geodésicas están numeradas en orden de longitud creciente. (Esta figura usa la misma posición para A que la Fig. 13 y está dibujada en la misma proyección). Las dos geodésicas más cortas son estables , es decir, m ₁₂ > 0 , de modo que no hay un camino cercano que conecte los dos puntos que sea más corto; las otras dos son inestables. Solo la línea más corta (la primera) tiene σ ₁₂ ≤ π . Todas las geodésicas son tangentes a la envolvente que se muestra en verde en la figura.

La astroide es la evoluta (exterior) de los círculos geodésicos centrados en A. Asimismo, los círculos geodésicos son involutas de la astroide.

Área de un polígono geodésico

Un polígono geodésico es un polígono cuyos lados son geodésicos. Es análogo a un polígono esférico , cuyos lados son círculos máximos. El área de un polígono de este tipo se puede encontrar calculando primero el área entre un segmento geodésico y el ecuador, es decir, el área del cuadrilátero AFHB en la figura 1 (Danielsen 1989). Una vez que se conoce esta área, el área de un polígono se puede calcular sumando las contribuciones de todos los bordes del polígono.

Aquí se desarrolla una expresión para el área S ₁₂ de AFHB siguiendo a Sjöberg (2006). El área de cualquier región cerrada del elipsoide es

${\displaystyle T=\int dT=\int {\frac {1}{K}}\cos \varphi \,d\varphi \,d\lambda ,}$

donde dT es un elemento del área de la superficie y K es la curvatura gaussiana . Ahora bien, el teorema de Gauss-Bonnet aplicado a un polígono geodésico establece

${\displaystyle \Gamma =\int K\,dT=\int \cos \varphi \,d\varphi \,d\lambda ,}$

dónde

${\displaystyle \Gamma =2\pi -\sum _{j}\theta _{j}}$

es el exceso geodésico y θ _j es el ángulo exterior en el vértice j . Al multiplicar la ecuación de Γ por R ₂ ² , donde R ₂ es el radio autálico , y restarlo de la ecuación de T se obtiene

${\displaystyle {\begin{aligned}T&=R_{2}^{2}\,\Gamma +\int \left({\frac {1}{K}}-R_{2}^{2}\right)\cos \varphi \,d\varphi \,d\lambda \\&=R_{2}^{2}\,\Gamma +\int \left({\frac {b^{2}}{{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}}-R_{2}^{2}\right)\cos \varphi \,d\varphi \,d\lambda ,\end{aligned}}}$

donde se ha sustituido el valor de K para un elipsoide . Aplicando esta fórmula al cuadrilátero AFHB , notando que Γ = α ₂ − α ₁ , y realizando la integral sobre φ se obtiene

${\displaystyle S_{12}=R_{2}^{2}(\alpha _{2}-\alpha _{1})+b^{2}\int _{\lambda _{1}}^{\lambda _{2}}\left({\frac {1}{2{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}}}+{\frac {\tanh ^{-1}(e\sin \varphi )}{2e\sin \varphi }}-{\frac {R_{2}^{2}}{b^{2}}}\right)\sin \varphi \,d\lambda ,}$

donde la integral se encuentra sobre la línea geodésica (de modo que φ es implícitamente una función de λ ). La integral se puede expresar como una serie válida para f pequeña (Danielsen 1989) (Karney 2013, §6 y apéndice).

El área de un polígono geodésico se obtiene sumando S ₁₂ sobre sus aristas. Este resultado se cumple siempre que el polígono no incluya un poste; si lo incluye, se debe sumar 2 π R ₂ ² a la suma. Si las aristas se especifican por sus vértices, entonces una expresión conveniente para el exceso geodésico E ₁₂ = α ₂ − α ₁ es

${\displaystyle \tan {\frac {E_{12}}{2}}={\frac {\sin {\tfrac {1}{2}}(\beta _{2}+\beta _{1})}{\cos {\tfrac {1}{2}}(\beta _{2}-\beta _{1})}}\tan {\frac {\omega _{12}}{2}}.}$

Solución de los problemas directos e inversos

Para resolver los problemas geodésicos es necesario mapear la geodésica sobre la esfera auxiliar y resolver el problema correspondiente en la navegación de círculo máximo . Al resolver el triángulo esférico "elemental" para NEP en la Fig. 5, se pueden emplear las reglas de Napier para triángulos cuadrantes .

${\displaystyle {\begin{aligned}\sin \alpha _{0}&=\sin \alpha \cos \beta =\tan \omega \cot \sigma ,\\\cos \sigma &=\cos \beta \cos \omega =\tan \alpha _{0}\cot \alpha ,\\\cos \alpha &=\cos \omega \cos \alpha _{0}=\cot \sigma \tan \beta ,\\\sin \beta &=\cos \alpha _{0}\sin \sigma =\cot \alpha \tan \omega ,\\\sin \omega &=\sin \sigma \sin \alpha =\tan \beta \tan \alpha _{0}.\end{aligned}}}$

El mapeo de la geodésica implica evaluar las integrales para la distancia, s , y la longitud, λ , ecuaciones (3) y (4) y estas dependen del parámetro α ₀ .

El manejo del problema directo es sencillo, porque α ₀ se puede determinar directamente a partir de las cantidades dadas φ ₁ y α ₁ ; para un ejemplo de cálculo, consulte Karney (2013).

En el caso del problema inverso, se da λ ₁₂ ; esto no se puede relacionar fácilmente con el ángulo esférico equivalente ω ₁₂ porque se desconoce α _0. Por lo tanto, la solución del problema requiere que α ₀ se encuentre de manera iterativa ( búsqueda de raíces ); consulte Karney (2013) para obtener más detalles.

En aplicaciones geodésicas, donde f es pequeño, las integrales se evalúan típicamente como una serie (Legendre 1806) (Oriani 1806) (Bessel 1825) (Helmert 1880) (Rainsford 1955) (Rapp 1993). Para f arbitraria , las integrales (3) y (4) se pueden encontrar por cuadratura numérica o expresándolas en términos de integrales elípticas (Legendre 1806) (Cayley 1870) (Karney 2024).

Vincenty (1975) proporciona soluciones para los problemas directos e inversos; estos se basan en una expansión en serie realizada hasta el tercer orden en el aplanamiento y proporcionan una precisión de aproximadamente0,1 mm para el elipsoide WGS84 ; sin embargo, el método inverso no logra converger para puntos casi antípodas.

Karney (2013) continúa las expansiones hasta el sexto orden, lo que es suficiente para proporcionar una precisión doble completa para | f | ≤ 1 ⁄ 50 y mejora la solución del problema inverso de modo que converja en todos los casos. Karney (2013, apéndice) extiende el método para utilizar integrales elípticas que se pueden aplicar a elipsoides con aplanamiento arbitrario.

Geodésicas sobre un elipsoide triaxial

La solución del problema geodésico para un elipsoide de revolución es matemáticamente sencilla: debido a la simetría, las geodésicas tienen una constante de movimiento , dada por la relación de Clairaut, lo que permite reducir el problema a cuadratura . A principios del siglo XIX (con el trabajo de Legendre , Oriani , Bessel , et al.), existía una comprensión completa de las propiedades de las geodésicas en un elipsoide de revolución.

Por otra parte, las geodésicas sobre un elipsoide triaxial (con tres ejes desiguales) no tienen una constante de movimiento obvia y, por lo tanto, representaron un problema desafiante sin resolver en la primera mitad del siglo XIX. En un artículo notable, Jacobi (1839) descubrió una constante de movimiento que permitió que este problema también se redujera a cuadratura (Klingenberg 1982, §3.5). ^[4]

Sistema de coordenadas elipsoide triaxial

Fig. 17. Coordenadas elipsoidales triaxiales.

Consideremos el elipsoide definido por

${\displaystyle h={\frac {X^{2}}{a^{2}}}+{\frac {Y^{2}}{b^{2}}}+{\frac {Z^{2}}{c^{2}}}=1,}$

donde ( X , Y , Z ) son coordenadas cartesianas centradas en el elipsoide y, sin pérdida de generalidad, a ≥ b ≥ c > 0 . ^[5]Jacobi (1866, §§26–27) empleó las coordenadas elipsoidales (triaxiales) (con latitud elipsoidal triaxial y longitud elipsoidal triaxial , β , ω ) definidas por

${\displaystyle {\begin{aligned}X&=a\cos \omega {\frac {\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {a^{2}-c^{2}}}},\\Y&=b\cos \beta \sin \omega ,\\Z&=c\sin \beta {\frac {\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {a^{2}-c^{2}}}}.\end{aligned}}}$

En el límite b → a , β se convierte en la latitud paramétrica de un elipsoide achatado, por lo que el uso del símbolo β es coherente con las secciones anteriores. Sin embargo, ω es diferente de la longitud esférica definida anteriormente. ^[6]

Las líneas de cuadrícula de constantes β (en azul) y ω (en verde) se dan en la Fig. 17. Estas constituyen un sistema de coordenadas ortogonales : las líneas de cuadrícula se intersecan en ángulos rectos. Las secciones principales del elipsoide, definidas por X = 0 y Z = 0 se muestran en rojo. La tercera sección principal, Y = 0 , está cubierta por las líneas β = ±90° y ω = 0° o ±180° . Estas líneas se encuentran en cuatro puntos umbilicales (dos de los cuales son visibles en esta figura) donde los radios principales de curvatura son iguales. Aquí y en las otras figuras de esta sección los parámetros del elipsoide son a : b : c = 1.01:1:0.8 , y se ve en una proyección ortográfica desde un punto por encima de φ = 40° , λ = 30° .

Las líneas de la cuadrícula de coordenadas elipsoidales se pueden interpretar de tres maneras diferentes:

1. Son "líneas de curvatura" en el elipsoide: son paralelas a las direcciones de curvatura principal (Monge 1796).
2. Son también intersecciones del elipsoide con sistemas confocales de hiperboloides de una y dos láminas (Dupin 1813, Parte 5).
3. Finalmente, están las elipses geodésicas y las hipérbolas definidas utilizando dos puntos umbilicales adyacentes (Hilbert y Cohn-Vossen 1952, p. 188). Por ejemplo, las líneas de constante β en la figura 17 se pueden generar con la conocida construcción de cuerdas para elipses con los extremos de la cuerda fijados a los dos puntos umbilicales.

La solución de Jacobi

Jacobi demostró que las ecuaciones geodésicas, expresadas en coordenadas elipsoidales, son separables. Así es como le contó su descubrimiento a su amigo y vecino Bessel (Jacobi 1839, Carta a Bessel):

Anteayer reduje a cuadratura el problema de las líneas geodésicas sobre un elipsoide con tres ejes desiguales . Son las fórmulas más sencillas del mundo, las integrales abelianas , que se convierten en las conocidas integrales elípticas si se igualan los 2 ejes.

Königsberg , 28 de diciembre de 1938.

La solución dada por Jacobi (Jacobi 1839) (Jacobi 1866, §28) es

${\displaystyle {\begin{aligned}\delta &=\int {\frac {{\sqrt {b^{2}\sin ^{2}\beta +c^{2}\cos ^{2}\beta }}\,d\beta }{{\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {{\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta -\gamma }}}}\\[6pt]&\quad -\int {\frac {{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega }}\,d\omega }{{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {{\bigl (}a^{2}-b^{2}{\bigr )}\sin ^{2}\omega +\gamma }}}}.\end{aligned}}}$

Como señala Jacobi, "una función del ángulo β es igual a una función del ángulo ω . Estas dos funciones son simplemente integrales abelianas..." . En la solución aparecen dos constantes δ y γ . Normalmente, δ es cero si los límites inferiores de las integrales se toman como el punto de inicio de la geodésica y la dirección de la geodésica está determinada por γ . Sin embargo, para las geodésicas que comienzan en puntos umbilicales, tenemos γ = 0 y δ determina la dirección en el punto umbilical. La constante γ puede expresarse como

${\displaystyle \gamma ={\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta \sin ^{2}\alpha -{\bigl (}a^{2}-b^{2}{\bigl )}\sin ^{2}\omega \cos ^{2}\alpha ,}$

donde α es el ángulo que forma la geodésica con las líneas de constante ω . En el límite b → a , esto se reduce a senα cos β = const. , la conocida relación de Clairaut. Darboux (1894, §§583–584) ofrece una derivación del resultado de Jacobi; él da la solución encontrada por Liouville (1846) para superficies cuadráticas generales.

Levantamiento de geodésicas triaxiales

Geodésicas circumpolares, ω ₁ =0° , α ₁ =90° .

En un elipsoide triaxial, solo hay tres geodésicas cerradas simples, las tres secciones principales del elipsoide dadas por X = 0 , Y = 0 y Z = 0 . ^[7] Para examinar las otras geodésicas, es conveniente considerar geodésicas que intersecan la sección principal media, Y = 0 , en ángulos rectos. Dichas geodésicas se muestran en las figuras 18-22, que utilizan los mismos parámetros de elipsoide y la misma dirección de visualización que la figura 17. Además, las tres elipses principales se muestran en rojo en cada una de estas figuras.

Si el punto de partida es β ₁ ∈ (−90°, 90°) , ω ₁ = 0 , y α ₁ = 90° , entonces γ > 0 y la geodésica rodea al elipsoide en un sentido "circumpolar". La geodésica oscila al norte y al sur del ecuador; en cada oscilación completa un poco menos de un circuito completo alrededor del elipsoide, lo que resulta, en el caso típico, en que la geodésica llena el área limitada por las dos líneas de latitud β = ± β ₁ . Se dan dos ejemplos en las figuras 18 y 19. La figura 18 muestra prácticamente el mismo comportamiento que para un elipsoide oblato de revolución (porque a ≈ b ); compárese con la Fig. 9. Sin embargo, si el punto de partida está en una latitud más alta (Fig. 18), las distorsiones resultantes de a ≠ b son evidentes. Todas las tangentes a una geodésica circumpolar tocan el hiperboloide confocal de una sola hoja que interseca el elipsoide en β = β ₁ (Chasles 1846) (Hilbert & Cohn-Vossen 1952, pp. 223–224).

Geodésicas transpolares, β ₁ =90° , α ₁ =180° .

Si el punto de partida es β ₁ = 90° , ω ₁ ∈ (0°, 180°) , y α ₁ = 180° , entonces γ < 0 y la geodésica rodea al elipsoide en un sentido "transpolar". La geodésica oscila al este y al oeste de la elipse X = 0 ; en cada oscilación completa un poco más de un circuito completo alrededor del elipsoide. En el caso típico, esto da como resultado que la geodésica llene el área limitada por las dos líneas de longitud ω = ω ₁ y ω = 180° − ω ₁ . Si a = b , todos los meridianos son geodésicas; el efecto de a ≠ b hace que dichas geodésicas oscilen al este y al oeste. Se dan dos ejemplos en las figuras 1 y 2. 20 y 21. La constricción de la geodésica cerca del polo desaparece en el límite b → c ; en este caso, el elipsoide se convierte en un elipsoide alargado y la Fig. 20 se parecería a la Fig. 10 (rotada de lado). Todas las tangentes a una geodésica transpolar tocan el hiperboloide de doble hoja confocal que interseca el elipsoide en ω = ω ₁ .

En las figuras 18-21, las geodésicas están (casi) cerradas. Como se señaló anteriormente, en el caso típico, las geodésicas no están cerradas, sino que llenan el área delimitada por las líneas límite de latitud (en el caso de las figuras 18-19) o longitud (en el caso de las figuras 20-21).

Fig. 22. Una geodésica umbilical, β ₁ =90° , ω ₁ =0° , α ₁ =135° .

Si el punto de partida es β ₁ = 90° , ω ₁ = 0° (un punto umbilical) y α ₁ = 135° (la geodésica sale de la elipse Y = 0 en ángulo recto), entonces γ = 0 y la geodésica intersecta repetidamente el punto umbilical opuesto y regresa a su punto de partida. Sin embargo, en cada circuito el ángulo en el que intersecta Y = 0 se acerca más a0° o180° de modo que asintóticamente la geodésica se encuentra sobre la elipse Y = 0 (Hart 1849) (Arnold 1989, p. 265), como se muestra en la Fig. 22. Una sola geodésica no llena un área en el elipsoide. Todas las tangentes a las geodésicas umbilicales tocan la hipérbola confocal que interseca el elipsoide en los puntos umbilicales.

Las geodésicas umbilicales gozan de varias propiedades interesantes.

• Por cualquier punto del elipsoide pasan dos geodésicas umbilicales.
• La distancia geodésica entre puntos umbilicales opuestos es la misma independientemente de la dirección inicial de la geodésica.
• Mientras que las geodésicas cerradas sobre las elipses X = 0 y Z = 0 son estables (una geodésica inicialmente cercana y casi paralela a la elipse permanece cerca de la elipse), la geodésica cerrada sobre la elipse Y = 0 , que pasa por los 4 puntos umbilicales, es exponencialmente inestable . Si se la perturba, se saldrá del plano Y = 0 y dará una vuelta antes de volver a estar cerca del plano. (Este comportamiento puede repetirse dependiendo de la naturaleza de la perturbación inicial).

Si el punto de partida A de una geodésica no es un punto umbilical, su envolvente es una astroide con dos cúspides que se encuentran en β = − β ₁ y las otras dos en ω = ω ₁ + π . El lugar geométrico de corte de A es la porción de la línea β = − β ₁ entre las cúspides.

Aplicaciones

Los problemas geodésicos directos e inversos ya no desempeñan el papel central en geodesia que tenían antes. En lugar de resolver el ajuste de redes geodésicas como un problema bidimensional en trigonometría esferoidal, estos problemas ahora se resuelven mediante métodos tridimensionales (Vincenty y Bowring 1978). No obstante, las geodésicas terrestres aún desempeñan un papel importante en varias áreas:

• para medir distancias y áreas en sistemas de información geográfica ;
• la definición de fronteras marítimas (UNCLOS 2006);
• en las reglas de la Administración Federal de Aviación para la navegación de área (RNAV 2007);
• el método de medición de distancias en el Código Deportivo de la FAI (FAI 2018).
• Ayudar a los musulmanes a encontrar su dirección hacia la Meca.

Por el principio de mínima acción , muchos problemas de física pueden formularse como un problema variacional similar al de las geodésicas. De hecho, el problema geodésico es equivalente al movimiento de una partícula obligada a moverse sobre la superficie, pero que, por lo demás, no está sujeta a ninguna fuerza (Laplace 1799a) (Hilbert y Cohn-Vossen 1952, p. 222). Por esta razón, las geodésicas sobre superficies simples, como los elipsoides de revolución o los elipsoides triaxiales, se utilizan con frecuencia como "casos de prueba" para explorar nuevos métodos. Algunos ejemplos son:

• el desarrollo de integrales elípticas (Legendre 1811) y funciones elípticas (Weierstrass 1861);
• el desarrollo de la geometría diferencial (Gauss 1828) (Christoffel 1869);
• métodos para resolver sistemas de ecuaciones diferenciales mediante un cambio de variables independientes (Jacobi 1839);
• el estudio de los cáusticos (Jacobi 1891);
• Investigaciones sobre el número y la estabilidad de las órbitas periódicas (Poincaré 1905);
• en el límite c → 0 , las geodésicas en un elipsoide triaxial se reducen a un caso de billar dinámico ;
• extensiones a un número arbitrario de dimensiones (Knörrer 1980);
• flujo geodésico sobre una superficie (Berger 2010, Cap. 12).

Véase también

• Rutas de la sección de la Tierra
• Figura de la Tierra
• Distancia geográfica
• Navegación de círculo máximo
• Gran elipse
• Geodésico
• Geodesia
• Proyección de mapas
  • Proyección cartográfica del elipsoide triaxial
• Arco meridiano
• Línea de rumbo
• Las fórmulas de Vincenty

Notas

1. Aquí α ₂ es el acimut frontal en B . Algunos autores calculan en cambio el acimut posterior ; este se da por α ₂ ± π .
2. Laplace (1799a) demostró que una partícula obligada a moverse sobre una superficie pero que no está sujeta a ninguna fuerza se mueve a lo largo de una geodésica para esa superficie. Por lo tanto, la relación de Clairaut es simplemente una consecuencia de la conservación del momento angular para una partícula en una superficie de revolución.
3. Bagratuni (1962, §17) utiliza el término "coeficiente de convergencia de ordenadas" para la escala geodésica.
4. Esta sección está adaptada de la documentación de GeographicLib (Karney 2015, Geodésicas en un elipsoide triaxial)
5. Esta notación para los semiejes es incompatible con la utilizada en la sección anterior sobre elipsoides de revolución, en la que a y b representaban el radio ecuatorial y el semieje polar. Por lo tanto, las desigualdades correspondientes son a = a ≥ b > 0 para un elipsoide achatado y b ≥ a = a > 0 para un elipsoide alargado.
6. El límite b → c da un elipsoide alargado con ω desempeñando el papel de latitud paramétrica.
7. Si c ⁄ a < 1 ⁄ 2 , existen otras geodésicas cerradas simples similares a las que se muestran en las figuras 11 y 12 (Klingenberg 1982, §3.5.19).

Referencias

• Arnold, VI (1989). Métodos matemáticos de la mecánica clásica . Traducido por Vogtmann, K.; Weinstein, A. (2.ª ed.). Springer-Verlag. ISBN 978-0-387-96890-2.OCLC 4037141  .
• Bagratuni, GV (1967) [1962]. Curso de Geodesia Esferoidal . doi :10.5281/zenodo.32371. OCLC  6150611.Traducción del ruso de Курс сфероидической геодезии (Moscú, 1962) por la Fuerza Aérea de EE. UU. (FTD-MT-64-390)
• Berger, M. (2010). Geometría revelada . Traducido por Senechal, L. J. Springer. doi :10.1007/978-3-540-70997-8. ISBN 978-3-540-70996-1.
• Bessel, FW (2010) [1825]. "El cálculo de longitud y latitud a partir de mediciones geodésicas". Astronomische Nachrichten . 331 (8). Traducido por Karney, CFF; Deakin, RE: 852–861. arXiv : 0908.1824 . Código Bibliográfico :2010AN....331..852K. doi :10.1002/asna.201011352. S2CID  118760590.Traducción al inglés de Astron. Nachr. 4, 241–254 (1825). Erratas.
• Bliss, GA (1916). "Condición de Jacobi para problemas de cálculo de variaciones en forma paramétrica". Transactions of the American Mathematical Society . 17 (2): 195–206. doi : 10.1090/S0002-9947-1916-1501037-4 .
• Bomford, G. (1952). Geodesia . Oxford: Clarendon. OCLC  1396190.
• Borre, K.; Strang, WG (2012). "11, Geometría del elipsoide" (PDF) . Algoritmos para posicionamiento global . Wellesley-Cambridge Press. ISBN 978-0-9802327-3-8.OCLC 795014501  .
• Cayley, A. (1870). "Sobre las líneas geodésicas en un esferoide achatado". Revista filosófica . 4.ª serie. 40 (268): 329–340. doi :10.1080/14786447008640411.
• Chasles, M. (1846). "Sur les lignes géodésiques et les lignes de courbure des Surfaces du second degré" [Líneas geodésicas y líneas de curvatura de las superficies de segundo grado]. Journal de Mathématiques Pures et Appliquées (en francés). 11 : 5–20.PDF.
• Christoffel, EB (1869). "Allgemeine Theorie der geodätischen Dreiecke" [Teoría general de los triángulos geodésicos]. Abhandlungen Königlichen Akademie der Wissenschaft zu Berlin (en alemán): 119-176.
• Claraut, AC (1735). "Détermination géometrique de la perpendiculaire à la méridienne tracée par M. Cassini" [Determinación geométrica de la perpendicular al meridiano dibujada por Jacques Cassini]. Mémoires de l'Académie Royale des Sciences de Paris 1733 (en francés): 406–416.
• Danielsen, JS (1989). "El área bajo la geodésica". Survey Review . 30 (232): 61–66. doi :10.1179/003962689791474267.
• Darboux, JG (1894). Leçons sur la théorie générale des Surfaces [ Lecciones sobre teoría general de superficies ] (en francés). vol. 3. París: Gauthier-Villars. OCLC  8566228.
• Dupin, PCF (1813). Développements de Géométrie [ Desarrollos en geometría ] (en francés). París: Courcier. OCLC  560800801.
• Ehlert, D. (1993). Methoden der ellipsoidischen Dreiecksberechnung [ Métodos de triangulación elipsoidal ] (Informe técnico). Reihe B: Angewandte Geodäsie, Heft Nr. 292 (en alemán). Comisión Geodätische Alemana. OCLC  257615376.
• Euler, L. (1755). "Élémens de la trigonométrie sphéroïdique tirés de la méthode des plus grands et plus petits" [Elementos de trigonometría esferoidal tomados del método de máximos y mínimos]. Mémoires de l'Académie Royale des Sciences de Berlin 1753 (en francés). 9 : 258–293.Figuras.
• FAI (2018). "Sección 8.2.3". Código deportivo FAI (PDF) (Informe técnico). Lausana, Suiza: Fédération Aéronautique Internationale.
• Forsyth, AR (1927). Cálculo de variaciones . Cambridge Univ. Press. ISBN 978-1-107-64083-2.OCLC 250050479  .
• Gan'shin, VV (1969) [1967]. Geometría del Elipsoide Terrestre . Traducido por Willis, JM St. Louis: Centro de información y cartas aeronáuticas. doi :10.5281/zenodo.32854. OCLC  493553.Traducción del ruso de Геометрия земного эллипсоида (Moscú, 1967).
• Gauss, CF (1902) [1828]. Investigaciones generales de superficies curvas de 1827 y 1825. Traducido por Morehead, JC; Hiltebeitel, AM Princeton Univ. Lib. OCLC  7824448.PDF. Traducción al inglés de Disquisitiones generales circa superficies curvas (Dieterich, Göttingen, 1828).
• Hart, AS (1849). "Demostración geométrica de algunas propiedades de las líneas geodésicas". Cambridge and Dublin Mathematical Journal . 4 : 80–84.
• Helmert, FR (1964) [1880]. Teorías matemáticas y físicas de la geodesia superior . Vol. 1. St. Louis: Centro de información y cartas aeronáuticas. doi :10.5281/zenodo.32050. OCLC  17273288.Traducción al inglés de Die Mathematischen und Physikalischen Theorieen der Höheren Geodäsie, vol. 1 (Teubner, Leipzig, 1880).
• Hilbert, D .; Cohn-Vossen, S. (1952). Geometría e imaginación . Traducido por Nemenyi, P. Nueva York: Chelsea. ISBN 9780828400879.OCLC 301610346  .
• Hutton, C. (1811). Un curso de matemáticas en tres volúmenes compuesto para uso de la Real Academia Militar. Vol. 3. Londres: FC y J. Rivington. OCLC  1803-1510.
• Jacobi, CGJ (1837). "Zur Theorie der Variations-Rechnung und der Differential-Gleichungen" [La teoría del cálculo de variaciones y de ecuaciones diferenciales]. Journal für die Reine und Angewandte Mathematik (en alemán). 1837 (17): 68–82. doi :10.1515/crll.1837.17.68. S2CID  119469290.
• Jacobi, CGJ (1839). "Note von der geodätischen Linie auf einem Ellipsoid und den verschiedenen Anwendungen einer merkwürdigen analytischen Substitution" [La geodésica sobre un elipsoide y diversas aplicaciones de una notable sustitución analítica]. Journal für die Reine und Angewandte Mathematik (en alemán). 1839 (19): 309–313. doi :10.1515/crll.1839.19.309. S2CID  121670851.Carta a Bessel, 28 de diciembre de 1838. Traducción francesa (1841).
• Jacobi, CGJ (2009) [1866]. A. Clebsch (ed.). Lecciones sobre dinámica . Traducido por Balagangadharan, K. Nueva Delhi: Hindustan Book Agency. ISBN 978-81-85931-91-3. Sr.  2569315. OCLC  440645889.Traducción al inglés de Vorlesungen über Dynamik (Reimer, Berlín, 1866). Erratas.
• Jacobi, CGJ (1891). "Über die Curve, welche alle von einem Punkte ausgehenden geodätischen Linien eines Rotationsellipsoides berührt" [La envoltura de líneas geodésicas que emanan de un solo punto en un elipsoide]. En KTW Weierstrass (ed.). Gesammelte Werke de Jacobi (en alemán). vol. 7. Berlín: Reimer. págs. 72–87. OCLC  630416023.Post. op., completado por FHA Wangerin . PDF.
• Jekeli, C. (2012), Sistemas de referencia geométrica en geodesia , Universidad Estatal de Ohio, hdl :1811/51274
• Jordan, W. ; Eggert, O. (1962) [1941]. Manual de geodesia . Vol. 3. Traducido por Carta, MW Washington, DC: Army Map Service. Bibcode :1962hage.book.....J. doi :10.5281/zenodo.35316. OCLC  34429043.Traducción al inglés del Handbuch der Vermessungskunde , 8.ª edición (Metzler, Stuttgart, 1941).
• Karney, CFF (2013). "Algoritmos para geodésicas". Journal of Geodesy . 87 (1): 43–55. arXiv : 1109.4448 . Código Bibliográfico :2013JGeod..87...43K. doi : 10.1007/s00190-012-0578-z .Adendas.
• Karney, CFF (2015). "GeographicLib". Versión 1.44.
• Karney, CFF (2024). "Geodésicas en un elipsoide arbitrario de revolución". Journal of Geodesy . 98 (1): 4:1–14. arXiv : 2208.00492 . doi : 10.1007/s00190-023-01813-2 .
• Klingenberg, WPA (1982). Geometría Riemanniana . de Gruyer. ISBN 978-3-11-008673-7. Sr.  0666697. OCLC  8476832.
• Knörrer, H. (1980). "Geodésicas sobre el elipsoide". Invenciones Mathematicae . 59 (2): 119-143. Código Bib : 1980 InMat..59..119K. doi :10.1007/BF01390041. S2CID  118792545.
• Krakiwsky, EJ; Thomson, DB (1974), Cálculos de posición geodésica (PDF) , Departamento de Geodesia e Ingeniería Geomática, Notas de clase, Fredericton, NB: Univ. de Nuevo Brunswick, Bibcode :1974gpc..book.....K
• Laplace, PS (1829) [1799a]. "Libro 1, §8". Tratado de mecánica celeste . Vol. 1. Traducido por Bowditch, N. Boston: Hillard, Gray, Little y Wilkins. OCLC  1294937.
• Laplace, PS (1799b). Traité de Mécanique Céleste [ Tratado de Mecánica Celeste ] (en francés). vol. 2. París: Crapelet. pag. 112. OCLC  25448952.
• Legendre, AM (1806). "Analyse des Triangles tracées sur la Surface d'un sphéroïde" [Análisis de triángulos esferoidales]. Mémoires de l'Institut National de France (en francés) (primer semestre): 130–161.
• Legendre, AM (1811). Exercices de Calcul Intégral sur Divers Ordres de Transcendentes et sur les Quadratures [ Ejercicios de cálculo integral ] (en francés). París: Courcier. OCLC  312469983.
• Leick, A.; Rapoport, L.; Tatarnikov, D. (2015). Topografía por satélite GPS (4ª ed.). Wiley. ISBN 978-1-119-01828-5.
• Liouville, J. (1846). "Sur quelques cas particuliers où les équations du mouvement d'un point matériel peuvent s'intégrer" [Sobre casos especiales en los que se pueden integrar las ecuaciones de movimiento de una partícula puntual]. Journal de Mathématiques Pures et Appliquées (en francés). 11 : 345–378.PDF
• Lyusternik, L. (1964). Shortest Paths: Variational Problems . Popular Lectures in Mathematics. Vol. 13. Traducido por Collins, P.; Brown, RB Nueva York: Macmillan. MR  0178386. OCLC  1048605.Traducción del ruso de Кратчайшие Линии: Вариационные Задачи (Moscú, 1955).
• Monge, G. (1850) [1796]. "Sur les lignes de courbure de la Surface de l'ellipsoïde" [Sobre las líneas de curvatura de la superficie del elipsoide]. En J. Liouville (ed.). Application de l'Analyse à la Géometrie (en francés) (5ª ed.). París: Bachiller. págs. 139-160. OCLC  2829112.(Fig. 1–2, Fig. 3–4). Edición de 1796 (Fig. 1–2, Fig. 3–4). Figuras en formato PDF.
• National Geodetic Survey (2012). "Utilidades geodésicas: inversas y directas". Versión 3.0.
• Newton, I. (1848) [1687]. "Libro 3, Proposición 19, Problema 3". Los principios matemáticos de la filosofía natural . Traducido por Motte, A. Nueva York: Adee. pp. 405–409.Traducción al inglés de Philosophiæ Naturalis Principia Mathematica . Liber Tertius, Proposición XIX. Prob. II. págs. 422–424.
• Oriani, B. (1806). "Elementi di trigonometria sferoidica, Pt. 1" [Elementos de trigonometría esferoidal]. Memorie dell'Istituto Nazionale Italiano (en italiano). 1 (1): 118–198.
• Oriani, B. (1808). "Elementi di trigonometria sferoidica, Pt. 2" [Elementos de trigonometría esferoidal]. Memorie dell'Istituto Nazionale Italiano (en italiano). 2 (1): 1–58.
• Oriani, B. (1810). "Elementi di trigonometria sferoidica, Pt. 3" [Elementos de trigonometría esferoidal]. Memorie dell'Istituto Nazionale Italiano (en italiano). 2 (2): 1–58.
• Poincaré, H. (1905). "Sur les lignes géodésiques des faces convexes" [Líneas geodésicas sobre superficies convexas]. Transacciones de la Sociedad Matemática Estadounidense (en francés). 6 (3): 237–274. doi :10.2307/1986219. JSTOR  1986219.
• Rainsford, HF (1955). "Geodésicas largas en el elipsoide". Bulletin Géodésique . 37 (1): 12–22. Bibcode :1955BGeod..29...12R. doi :10.1007/BF02527187. S2CID  122111614.
• Rapp, RH (1991), Geodesia geométrica, parte I , Universidad Estatal de Ohio, hdl :1811/24333
• Rapp, RH (1993), Geodesia geométrica, parte II , Universidad Estatal de Ohio, hdl :1811/24409
• RNAV (2007). "Apéndice 2". Orden 8260.54A, Norma de los Estados Unidos para la Navegación de Área (PDF) (Informe técnico). Washington, DC: Administración Federal de Aviación de los Estados Unidos.
• Sjöberg, LE (2006). "Determinación de áreas en el plano, esfera y elipsoide". Survey Review . 38 (301): 583–593. doi :10.1179/003962606780732100.
• UNCLOS (2006). Manual sobre los aspectos técnicos de la Convención de las Naciones Unidas sobre el Derecho del Mar, 1982 (PDF) (Informe técnico) (4ª ed.). Mónaco: Oficina Hidrográfica Internacional. Archivado desde el original (PDF) el 24 de mayo de 2013. Consultado el 15 de agosto de 2013 .
• Vincenty, T. (1975). "Soluciones directas e inversas de geodésicas sobre el elipsoide con aplicación de ecuaciones anidadas" (PDF) . Survey Review . 23 (176): 88–93. Bibcode :1975SurRv..23...88V. doi :10.1179/sre.1975.23.176.88. Adición: Survey Review 23 (180): 294 (1976).
• Vincenty, T. ; Bowring, BR (1978). Aplicación de la geodesia tridimensional a los ajustes de redes horizontales (PDF) (Informe técnico). NOAA. NOS NGS-13.
• Weierstrass, KTW (1861). "Über die geodätischen Linien auf dem dreiaxigen Ellipsoid" [Líneas geodésicas en un elipsoide triaxial]. Monatsberichte der Königlichen Akademie der Wissenschaft zu Berlin (en alemán): 986–997.

Enlaces externos

• Bibliografía geodésica en línea de libros y artículos sobre geodésicas en elipsoides.
• Conjunto de pruebas para geodésicas, un conjunto de 500000 geodésicas para el elipsoide WGS84, calculadas utilizando aritmética de alta precisión.
• Herramienta NGS que implementa Vincenty (1975).
• geod(1), página de manual de la utilidad PROJ para cálculos geodésicos.
• Implementación de GeographicLib de Karney (2013).
• Dibujar geodésicas en Google Maps.