Espacio dual

En matemáticas, espacio vectorial de formas lineales.

En matemáticas , cualquier espacio vectorial tiene un espacio vectorial dual correspondiente (o simplemente espacio dual para abreviar) que consiste en todas las formas lineales junto con la estructura del espacio vectorial de adición puntual y multiplicación escalar por constantes. ${\displaystyle V}$ ${\displaystyle V,}$

El espacio dual, tal como se definió anteriormente, se define para todos los espacios vectoriales y, para evitar ambigüedades, también se lo puede llamar espacio dual algebraico . Cuando se define para un espacio vectorial topológico , existe un subespacio del espacio dual, correspondiente a los funcionales lineales continuos , llamado espacio dual continuo .

Los espacios vectoriales duales se utilizan en muchas ramas de las matemáticas que utilizan espacios vectoriales, como en el análisis tensorial con espacios vectoriales de dimensión finita . Cuando se aplican a espacios vectoriales de funciones (que normalmente son de dimensión infinita), los espacios duales se utilizan para describir medidas , distribuciones y espacios de Hilbert . En consecuencia, el espacio dual es un concepto importante en el análisis funcional .

Los primeros términos para dual incluyen espacio polarizado [Hahn 1927], espacio conjugado , espacio adjunto [Alaoglu 1940] y espacio transponido [Schauder 1930] y [Banach 1932]. El término dual se debe a Bourbaki 1938. ^[1]

Espacio dual algebraico

Dado cualquier espacio vectorial sobre un cuerpo , el espacio dual (algebraico) ^[2] (alternativamente denotado por ^[3] o ^{[4] [5]} ) ^{[nb 1]} se define como el conjunto de todos los mapas lineales ( funcionales lineales ). Dado que los mapas lineales son homomorfismos del espacio vectorial , el espacio dual puede denotarse . ^[3] El espacio dual en sí mismo se convierte en un espacio vectorial sobre cuando se lo equipa con una adición y una multiplicación escalar que satisfacen: ${\displaystyle V}$ ${\displaystyle F}$ ${\displaystyle V^{*}}$ ${\displaystyle V^{\lor }}$ ${\displaystyle V'}$ ${\displaystyle \varphi :V\to F}$ ${\displaystyle \hom(V,F)}$ ${\displaystyle V^{*}}$ ${\displaystyle F}$

${\displaystyle {\begin{aligned}(\varphi +\psi )(x)&=\varphi (x)+\psi (x)\\(a\varphi )(x)&=a\left(\varphi (x)\right)\end{aligned}}}$

para todos , , y . ${\displaystyle \varphi ,\psi \in V^{*}}$ ${\displaystyle x\in V}$ ${\displaystyle a\in F}$

Los elementos del espacio dual algebraico a veces se denominan covectores , formas unitarias o formas lineales . ${\displaystyle V^{*}}$

El emparejamiento de un funcional en el espacio dual y un elemento de a veces se denota mediante un corchete: ^[6] o . ^[7] Este emparejamiento define una aplicación bilineal no degenerada ^{[nb 2]} llamada emparejamiento natural . ${\displaystyle \varphi }$ ${\displaystyle V^{*}}$ ${\displaystyle x}$ ${\displaystyle V}$ ${\displaystyle \varphi (x)=[x,\varphi ]}$ ${\displaystyle \varphi (x)=\langle x,\varphi \rangle }$ ${\displaystyle \langle \cdot ,\cdot \rangle :V\times V^{*}\to F}$

Caso de dimensión finita

Si es de dimensión finita, entonces tiene la misma dimensión que . Dada una base en , es posible construir una base específica en , llamada base dual . Esta base dual es un conjunto de funcionales lineales en , definidos por la relación ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle V}$ ${\displaystyle \{\mathbf {e} _{1},\dots ,\mathbf {e} _{n}\}}$ ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle \{\mathbf {e} ^{1},\dots ,\mathbf {e} ^{n}\}}$ ${\displaystyle V}$

${\displaystyle \mathbf {e} ^{i}(c^{1}\mathbf {e} _{1}+\cdots +c^{n}\mathbf {e} _{n})=c^{i},\quad i=1,\ldots ,n}$

para cualquier elección de coeficientes . En particular, haciendo que cada uno de esos coeficientes sea a su vez igual a uno y los otros coeficientes cero, se obtiene el sistema de ecuaciones ${\displaystyle c^{i}\in F}$

${\displaystyle \mathbf {e} ^{i}(\mathbf {e} _{j})=\delta _{j}^{i}}$

donde es el símbolo delta de Kronecker . Esta propiedad se denomina propiedad de biortogonalidad . ${\displaystyle \delta _{j}^{i}}$

Por ejemplo, si es , supongamos que su base es . Los vectores base no son ortogonales entre sí. Entonces, y son formas unitarias (funciones que asignan un vector a un escalar) tales que , , y . (Nota: El superíndice aquí es el índice, no un exponente). Este sistema de ecuaciones se puede expresar utilizando la notación matricial como ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \{\mathbf {e} _{1}=(1/2,1/2),\mathbf {e} _{2}=(0,1)\}}$ ${\displaystyle \mathbf {e} ^{1}}$ ${\displaystyle \mathbf {e} ^{2}}$ ${\displaystyle \mathbf {e} ^{1}(\mathbf {e} _{1})=1}$ ${\displaystyle \mathbf {e} ^{1}(\mathbf {e} _{2})=0}$ ${\displaystyle \mathbf {e} ^{2}(\mathbf {e} _{1})=0}$ ${\displaystyle \mathbf {e} ^{2}(\mathbf {e} _{2})=1}$

${\displaystyle {\begin{bmatrix}e^{11}&e^{12}\\e^{21}&e^{22}\end{bmatrix}}{\begin{bmatrix}e_{11}&e_{21}\\e_{12}&e_{22}\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\end{bmatrix}}.}$

Al resolver los valores desconocidos en la primera matriz, se muestra que la base dual es . Como y son funcionales, se pueden reescribir como y . ${\displaystyle \{\mathbf {e} ^{1}=(2,0),\mathbf {e} ^{2}=(-1,1)\}}$ ${\displaystyle \mathbf {e} ^{1}}$ ${\displaystyle \mathbf {e} ^{2}}$ ${\displaystyle \mathbf {e} ^{1}(x,y)=2x}$ ${\displaystyle \mathbf {e} ^{2}(x,y)=-x+y}$

En general, cuando es , si es una matriz cuyas columnas son los vectores base y es una matriz cuyas columnas son los vectores base duales, entonces ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle E=[\mathbf {e} _{1}|\cdots |\mathbf {e} _{n}]}$ ${\displaystyle {\hat {E}}=[\mathbf {e} ^{1}|\cdots |\mathbf {e} ^{n}]}$

${\displaystyle {\hat {E}}^{\textrm {T}}\cdot E=I_{n},}$

donde es la matriz identidad de orden . La propiedad de biortogonalidad de estos dos conjuntos base permite representar cualquier punto como ${\displaystyle I_{n}}$ ${\displaystyle n}$ ${\displaystyle \mathbf {x} \in V}$

${\displaystyle \mathbf {x} =\sum _{i}\langle \mathbf {x} ,\mathbf {e} ^{i}\rangle \mathbf {e} _{i}=\sum _{i}\langle \mathbf {x} ,\mathbf {e} _{i}\rangle \mathbf {e} ^{i},}$

incluso cuando los vectores base no son ortogonales entre sí. Estrictamente hablando, la afirmación anterior solo tiene sentido una vez que se introducen el producto interno y el emparejamiento de dualidad correspondiente, como se describe a continuación en § Productos bilineales y espacios duales . ${\displaystyle \langle \cdot ,\cdot \rangle }$

En particular, se puede interpretar como el espacio de columnas de números reales , su espacio dual se escribe típicamente como el espacio de filas de números reales. Tal fila actúa como un funcional lineal por multiplicación de matrices ordinarias . Esto se debe a que un funcional asigna cada -vector a un número real . Entonces, viendo este funcional como una matriz , y como una matriz, y una matriz (trivialmente, un número real) respectivamente, si entonces, por razones de dimensión, debe ser una matriz; es decir, debe ser un vector fila. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle n\times 1}$ ${\displaystyle y}$ ${\displaystyle 1\times 1}$ ${\displaystyle Mx=y}$ ${\displaystyle M}$ ${\displaystyle 1\times n}$ ${\displaystyle M}$

Si consiste en el espacio de vectores geométricos en el plano, entonces las curvas de nivel de un elemento de forman una familia de líneas paralelas en , porque el rango es unidimensional, de modo que cada punto en el rango es un múltiplo de cualquier elemento distinto de cero. Por lo tanto, un elemento de puede considerarse intuitivamente como una familia particular de líneas paralelas que cubren el plano. Para calcular el valor de un funcional en un vector dado, basta con determinar en cuál de las líneas se encuentra el vector. De manera informal, esto "cuenta" cuántas líneas cruza el vector. De manera más general, si es un espacio vectorial de cualquier dimensión, entonces los conjuntos de niveles de un funcional lineal en son hiperplanos paralelos en , y la acción de un funcional lineal en un vector puede visualizarse en términos de estos hiperplanos. ^[8] ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle V}$

Caso de dimensión infinita

Si no es de dimensión finita pero tiene una base ^{[nb 3]} indexada por un conjunto infinito , entonces la misma construcción que en el caso de dimensión finita produce elementos linealmente independientes ( ) del espacio dual, pero no formarán una base. ${\displaystyle V}$ ${\displaystyle \mathbf {e} _{\alpha }}$ ${\displaystyle A}$ ${\displaystyle \mathbf {e} ^{\alpha }}$ ${\displaystyle \alpha \in A}$

Por ejemplo, considere el espacio , cuyos elementos son aquellas secuencias de números reales que contienen solo un número finito de elementos distintos de cero, que tiene una base indexada por los números naturales . Para , es la secuencia que consta de todos los ceros excepto en la posición -ésima, que es 1. El espacio dual de es (isomorfo a) , el espacio de todas las secuencias de números reales: cada secuencia real define una función donde el elemento de se envía al número ${\displaystyle \mathbb {R} ^{\infty }}$ ${\displaystyle \mathbb {N} }$ ${\displaystyle i\in \mathbb {N} }$ ${\displaystyle \mathbf {e} _{i}}$ ${\displaystyle i}$ ${\displaystyle \mathbb {R} ^{\infty }}$ ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ ${\displaystyle (a_{n})}$ ${\displaystyle (x_{n})}$ ${\displaystyle \mathbb {R} ^{\infty }}$

${\displaystyle \sum _{n}a_{n}x_{n},}$

que es una suma finita porque solo hay un número finito de números distintos de cero . La dimensión de es infinitamente numerable , mientras que no tiene una base numerable. ${\displaystyle x_{n}}$ ${\displaystyle \mathbb {R} ^{\infty }}$ ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$

Esta observación se generaliza a cualquier espacio vectorial de dimensión infinita ^{[nb 3]} sobre cualquier cuerpo : una elección de base se identifica con el espacio de funciones tal que es distinto de cero solo para un número finito de , donde dicha función se identifica con el vector ${\displaystyle V}$ ${\displaystyle F}$ ${\displaystyle \{\mathbf {e} _{\alpha }:\alpha \in A\}}$ ${\displaystyle V}$ ${\displaystyle (F^{A})_{0}}$ ${\displaystyle f:A\to F}$ ${\displaystyle f_{\alpha }=f(\alpha )}$ ${\displaystyle \alpha \in A}$ ${\displaystyle f}$

${\displaystyle \sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }}$

en (la suma es finita por el supuesto de , y cualquier puede escribirse de forma única de esta manera por la definición de la base). ${\displaystyle V}$ ${\displaystyle f}$ ${\displaystyle v\in V}$

El espacio dual de puede entonces identificarse con el espacio de todas las funciones desde hasta : una función lineal en está determinada únicamente por los valores que toma sobre la base de , y cualquier función (con ) define una función lineal en por ${\displaystyle V}$ ${\displaystyle F^{A}}$ ${\displaystyle A}$ ${\displaystyle F}$ ${\displaystyle T}$ ${\displaystyle V}$ ${\displaystyle \theta _{\alpha }=T(\mathbf {e} _{\alpha })}$ ${\displaystyle V}$ ${\displaystyle \theta :A\to F}$ ${\displaystyle \theta (\alpha )=\theta _{\alpha }}$ ${\displaystyle T}$ ${\displaystyle V}$

${\displaystyle T\left(\sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }\right)=\sum _{\alpha \in A}f_{\alpha }T(e_{\alpha })=\sum _{\alpha \in A}f_{\alpha }\theta _{\alpha }.}$

Nuevamente, la suma es finita porque es distinta de cero solo para un número finito de . ${\displaystyle f_{\alpha }}$ ${\displaystyle \alpha }$

El conjunto puede identificarse (esencialmente por definición) con la suma directa de infinitas copias de (visto como un espacio vectorial unidimensional sobre sí mismo) indexado por , es decir, existen isomorfismos lineales ${\displaystyle (F^{A})_{0}}$ ${\displaystyle F}$ ${\displaystyle A}$

${\displaystyle V\cong (F^{A})_{0}\cong \bigoplus _{\alpha \in A}F.}$

Por otra parte, es (de nuevo por definición), el producto directo de infinitas copias de indexado por , y por lo tanto la identificación ${\displaystyle F^{A}}$ ${\displaystyle F}$ ${\displaystyle A}$

${\displaystyle V^{*}\cong \left(\bigoplus _{\alpha \in A}F\right)^{*}\cong \prod _{\alpha \in A}F^{*}\cong \prod _{\alpha \in A}F\cong F^{A}}$

es un caso especial de un resultado general que relaciona sumas directas (de módulos ) con productos directos.

Si un espacio vectorial no es finito-dimensional, entonces su espacio dual (algebraico) es siempre de mayor dimensión (como un número cardinal ) que el espacio vectorial original. Esto contrasta con el caso del espacio dual continuo, que se analiza más adelante, que puede ser isomorfo al espacio vectorial original incluso si este último es de dimensión infinita.

La prueba de esta desigualdad entre dimensiones resulta de lo siguiente.

Si es un espacio vectorial de dimensión infinita , las propiedades aritméticas de los números cardinales implican que ${\displaystyle V}$ ${\displaystyle F}$

${\displaystyle \mathrm {dim} (V)=|A|<|F|^{|A|}=|V^{\ast }|=\mathrm {max} (|\mathrm {dim} (V^{\ast })|,|F|),}$

donde las cardinalidades se denotan como valores absolutos . Para probarlo basta con probar que lo cual se puede hacer con un argumento similar al argumento diagonal de Cantor . ^[9] La dimensión exacta del dual está dada por el teorema de Erdős–Kaplansky . ${\displaystyle \mathrm {dim} (V)<\mathrm {dim} (V^{*}),}$ ${\displaystyle |F|\leq |\mathrm {dim} (V^{\ast })|,}$

Productos bilineales y espacios duales

Si V es de dimensión finita, entonces V es isomorfo a V ^∗ . Pero en general no hay isomorfismo natural entre estos dos espacios. ^[10] Cualquier forma bilineal ⟨·,·⟩ en V da una aplicación de V en su espacio dual mediante

${\displaystyle v\mapsto \langle v,\cdot \rangle }$

donde el lado derecho se define como el funcional en V que toma cada w ∈ V como ⟨ v , w ⟩ . En otras palabras, la forma bilineal determina una aplicación lineal

${\displaystyle \Phi _{\langle \cdot ,\cdot \rangle }:V\to V^{*}}$

definido por

${\displaystyle \left[\Phi _{\langle \cdot ,\cdot \rangle }(v),w\right]=\langle v,w\rangle .}$

Si la forma bilineal no es degenerada , entonces es un isomorfismo sobre un subespacio de V ^∗ . Si V es de dimensión finita, entonces es un isomorfismo sobre todo V ^∗ . Por el contrario, cualquier isomorfismo de V a un subespacio de V ^∗ (resp., todo V ^∗ si V es de dimensión finita) define una única forma bilineal no degenerada sobre V por ${\displaystyle \Phi }$ ${\displaystyle \langle \cdot ,\cdot \rangle _{\Phi }}$

${\displaystyle \langle v,w\rangle _{\Phi }=(\Phi (v))(w)=[\Phi (v),w].\,}$

Por lo tanto, existe una correspondencia biunívoca entre los isomorfismos de V a un subespacio de (o, todo) V ^∗ y las formas bilineales no degeneradas en V .

Si el espacio vectorial V está sobre el cuerpo complejo , entonces a veces es más natural considerar formas sesquilíneas en lugar de formas bilineales. En ese caso, una forma sesquilínea dada ⟨·,·⟩ determina un isomorfismo de V con el conjugado complejo del espacio dual

${\displaystyle \Phi _{\langle \cdot ,\cdot \rangle }:V\to {\overline {V^{*}}}.}$

El conjugado del espacio dual se puede identificar con el conjunto de todos los funcionales complejos aditivos f  : V → C tales que ${\displaystyle {\overline {V^{*}}}}$

${\displaystyle f(\alpha v)={\overline {\alpha }}f(v).}$

Inyección en el doble-dual

Existe un homomorfismo natural de en el doble dual , definido por para todo . En otras palabras, si es la función de evaluación definida por , entonces se define como la función . Esta función es siempre inyectiva ; ^{[nb 3]} y siempre es un isomorfismo si es de dimensión finita. ^[11] De hecho, el isomorfismo de un espacio vectorial de dimensión finita con su doble dual es un ejemplo arquetípico de un isomorfismo natural . Los espacios de Hilbert de dimensión infinita no son isomorfos a sus dobles duales algebraicos, sino a sus dobles duales continuos. ${\displaystyle \Psi }$ ${\displaystyle V}$ ${\displaystyle V^{**}=\{\Phi :V^{*}\to F:\Phi \ \mathrm {linear} \}}$ ${\displaystyle (\Psi (v))(\varphi )=\varphi (v)}$ ${\displaystyle v\in V,\varphi \in V^{*}}$ ${\displaystyle \mathrm {ev} _{v}:V^{*}\to F}$ ${\displaystyle \varphi \mapsto \varphi (v)}$ ${\displaystyle \Psi :V\to V^{**}}$ ${\displaystyle v\mapsto \mathrm {ev} _{v}}$ ${\displaystyle \Psi }$ ${\displaystyle V}$

Transposición de una función lineal

Si f  : V → W es una función lineal , entonces la transpuesta (o dual ) f ^∗  : W ^∗ → V ^∗ está definida por

${\displaystyle f^{*}(\varphi )=\varphi \circ f\,}$

para cada . La función resultante en se llama retroceso de a lo largo de . ${\displaystyle \varphi \in W^{*}}$ ${\displaystyle f^{*}(\varphi )}$ ${\displaystyle V^{*}}$ ${\displaystyle \varphi }$ ${\displaystyle f}$

La siguiente identidad es válida para todos y : ${\displaystyle \varphi \in W^{*}}$ ${\displaystyle v\in V}$

${\displaystyle [f^{*}(\varphi ),\,v]=[\varphi ,\,f(v)],}$

donde el corchete [·,·] de la izquierda es el emparejamiento natural de V con su espacio dual, y el de la derecha es el emparejamiento natural de W con su dual. Esta identidad caracteriza la transpuesta, ^[12] y es formalmente similar a la definición del adjunto .

La asignación f ↦ f ^∗ produce una función lineal inyectiva entre el espacio de operadores lineales de V a W y el espacio de operadores lineales de W ^∗ a V ^∗ ; este homomorfismo es un isomorfismo si y solo si W es de dimensión finita. Si V = W entonces el espacio de funciones lineales es en realidad un álgebra bajo composición de funciones , y la asignación es entonces un antihomomorfismo de álgebras, lo que significa que ( fg ) ^∗ = g ^∗ f ^∗ . En el lenguaje de la teoría de categorías , tomar el dual de espacios vectoriales y la transpuesta de funciones lineales es, por lo tanto, un funtor contravariante de la categoría de espacios vectoriales sobre F a sí mismo. Es posible identificar ( f ^∗ ) ^∗ con f usando la inyección natural en el dual doble.

Si la función lineal f está representada por la matriz A con respecto a dos bases de V y W , entonces f ^∗ está representada por la matriz transpuesta A ^T con respecto a las bases duales de W ^∗ y V ^∗ , de ahí el nombre. Alternativamente, como f está representada por A actuando a la izquierda sobre vectores columna, f ^∗ está representada por la misma matriz actuando a la derecha sobre vectores fila. Estos puntos de vista están relacionados por el producto interno canónico sobre R ⁿ , que identifica el espacio de vectores columna con el espacio dual de vectores fila.

Espacios cocientes y aniquiladores

Sea un subconjunto de . El aniquilador de en , denotado aquí , es la colección de funcionales lineales tales que para todo . Es decir, consta de todos los funcionales lineales tales que la restricción a se anula: . Dentro de espacios vectoriales de dimensión finita, el aniquilador es dual a (isomorfo a) el complemento ortogonal . ${\displaystyle S}$ ${\displaystyle V}$ ${\displaystyle S}$ ${\displaystyle V^{*}}$ ${\displaystyle S^{0}}$ ${\displaystyle f\in V^{*}}$ ${\displaystyle [f,s]=0}$ ${\displaystyle s\in S}$ ${\displaystyle S^{0}}$ ${\displaystyle f:V\to F}$ ${\displaystyle S}$ ${\displaystyle f|_{S}=0}$

El aniquilador de un subconjunto es en sí mismo un espacio vectorial. El aniquilador del vector cero es todo el espacio dual: , y el aniquilador de todo el espacio es simplemente el covector cero: . Además, la asignación de un aniquilador a un subconjunto de invierte las inclusiones, de modo que si , entonces ${\displaystyle \{0\}^{0}=V^{*}}$ ${\displaystyle V^{0}=\{0\}\subseteq V^{*}}$ ${\displaystyle V}$ ${\displaystyle \{0\}\subseteq S\subseteq T\subseteq V}$

${\displaystyle \{0\}\subseteq T^{0}\subseteq S^{0}\subseteq V^{*}.}$

Si y son dos subconjuntos de entonces ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle V}$

${\displaystyle A^{0}+B^{0}\subseteq (A\cap B)^{0}.}$

Si hay una familia de subconjuntos de indexados por pertenecer a algún conjunto de índices , entonces ${\displaystyle (A_{i})_{i\in I}}$ ${\displaystyle V}$ ${\displaystyle i}$ ${\displaystyle I}$

${\displaystyle \left(\bigcup _{i\in I}A_{i}\right)^{0}=\bigcap _{i\in I}A_{i}^{0}.}$

En particular, si y son subespacios de entonces ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle V}$

${\displaystyle (A+B)^{0}=A^{0}\cap B^{0}}$

y ^{[nb 3]}

${\displaystyle (A\cap B)^{0}=A^{0}+B^{0}.}$

Si es de dimensión finita y es un subespacio vectorial , entonces ${\displaystyle V}$ ${\displaystyle W}$

${\displaystyle W^{00}=W}$

después de identificarse con su imagen en el segundo espacio dual bajo el isomorfismo de doble dualidad . En particular, la formación del aniquilador es una conexión de Galois en la red de subconjuntos de un espacio vectorial de dimensión finita. ${\displaystyle W}$ ${\displaystyle V\approx V^{**}}$

Si es un subespacio de entonces el espacio cociente es un espacio vectorial por derecho propio, y por lo tanto tiene un dual. Por el primer teorema de isomorfismo , un funcional se factoriza mediante si y solo si está en el núcleo de . Por lo tanto, existe un isomorfismo ${\displaystyle W}$ ${\displaystyle V}$ ${\displaystyle V/W}$ ${\displaystyle f:V\to F}$ ${\displaystyle V/W}$ ${\displaystyle W}$ ${\displaystyle f}$

${\displaystyle (V/W)^{*}\cong W^{0}.}$

Como consecuencia particular, si es una suma directa de dos subespacios y , entonces es una suma directa de y . ${\displaystyle V}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle V^{*}}$ ${\displaystyle A^{0}}$ ${\displaystyle B^{0}}$

Análisis dimensional

El espacio dual es análogo a un espacio de dimensión "negativa". En términos más simples, dado que un vector se puede emparejar con un covector mediante el emparejamiento natural para obtener un escalar, un covector puede "cancelar" la dimensión de un vector, de manera similar a reducir una fracción . Por lo tanto, mientras que la suma directa es un espacio de dimensión ⁠ ⁠ (si ⁠ ⁠ es ⁠ ⁠ -dimensional), ⁠ ⁠ se comporta como un espacio de dimensión ⁠ ⁠ -dimensional, en el sentido de que sus dimensiones se pueden cancelar contra las dimensiones de ⁠ ⁠ . Esto se formaliza mediante la contracción tensorial . ${\displaystyle v\in V}$ ${\displaystyle \varphi \in V^{*}}$ ${\displaystyle \langle x,\varphi \rangle :=\varphi (x)\in F}$ ${\displaystyle V\oplus V^{*}}$ ${\displaystyle 2n}$ ${\displaystyle V}$ ${\displaystyle n}$ ${\displaystyle V^{*}}$ ${\displaystyle (-n)}$ ${\displaystyle V}$

Esto surge en física a través del análisis dimensional , donde el espacio dual tiene unidades inversas. ^[13] Bajo el emparejamiento natural, estas unidades se cancelan y el valor escalar resultante es adimensional , como se esperaba. Por ejemplo, en el análisis de Fourier (continuo) , o más ampliamente en el análisis de tiempo-frecuencia : ^{[nb 4]} dado un espacio vectorial unidimensional con una unidad de tiempo , el ${\displaystyle t}$ espacio dual tiene unidades de frecuencia : ocurrencias por unidad de tiempo (unidades de ) . ${\displaystyle 1/t}$ Por ejemplo, si el tiempo se mide en segundos , la unidad dual correspondiente es el segundo inverso : en el transcurso de 3 segundos, un evento que ocurre 2 veces por segundo ocurre un total de 6 veces, lo que corresponde a . De manera similar, si el espacio primario mide la longitud, el espacio dual mide la longitud inversa . ${\displaystyle 3s\cdot 2s^{-1}=6}$

Espacio dual continuo

Cuando se trabaja con espacios vectoriales topológicos , los funcionales lineales continuos del espacio en el cuerpo base (o ) son particularmente importantes. Esto da lugar a la noción de "espacio dual continuo" o "dual topológico", que es un subespacio lineal del espacio dual algebraico , denotado por . Para cualquier espacio vectorial normado de dimensión finita o espacio vectorial topológico, como el espacio n euclidiano , el dual continuo y el dual algebraico coinciden. Sin embargo, esto es falso para cualquier espacio normado de dimensión infinita, como lo demuestra el ejemplo de las aplicaciones lineales discontinuas . Sin embargo, en la teoría de espacios vectoriales topológicos , los términos "espacio dual continuo" y "espacio dual topológico" a menudo se reemplazan por "espacio dual". ${\displaystyle \mathbb {F} =\mathbb {C} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle V^{*}}$ ${\displaystyle V'}$

Para un espacio vectorial topológico su espacio dual continuo , ^[14] o espacio dual topológico , ^[15] o simplemente espacio dual ^{[14] [15] [16] [17]} (en el sentido de la teoría de espacios vectoriales topológicos) se define como el espacio de todos los funcionales lineales continuos . ${\displaystyle V}$ ${\displaystyle V'}$ ${\displaystyle \varphi :V\to {\mathbb {F} }}$

Ejemplos importantes de espacios duales continuos son el espacio de funciones de prueba con soporte compacto y su dual , el espacio de distribuciones arbitrarias (funciones generalizadas); el espacio de funciones de prueba arbitrarias y su dual , el espacio de distribuciones con soporte compacto; y el espacio de funciones de prueba de rápida disminución, el espacio de Schwartz , y su dual, el espacio de distribuciones templadas (distribuciones de crecimiento lento) en la teoría de funciones generalizadas . ${\displaystyle {\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}',}$ ${\displaystyle {\mathcal {E}}}$ ${\displaystyle {\mathcal {E}}',}$ ${\displaystyle {\mathcal {S}},}$ ${\displaystyle {\mathcal {S}}',}$

Propiedades

Si X es un espacio vectorial topológico de Hausdorff ( TVS), entonces el espacio dual continuo de X es idéntico al espacio dual continuo de la completitud de X. ^[1]

Topologías en el dual

Existe una construcción estándar para introducir una topología en el dual continuo de un espacio vectorial topológico . Fije una colección de subconjuntos acotados de . Esto da la topología en de convergencia uniforme en conjuntos de o lo que es lo mismo, la topología generada por seminormas de la forma ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}},}$

${\displaystyle \|\varphi \|_{A}=\sup _{x\in A}|\varphi (x)|,}$

donde es una función lineal continua en , y se ejecuta sobre la clase ${\displaystyle \varphi }$ ${\displaystyle V}$ ${\displaystyle A}$ ${\displaystyle {\mathcal {A}}.}$

Esto significa que una red de funcionales tiende a un funcional en si y sólo si ${\displaystyle \varphi _{i}}$ ${\displaystyle \varphi }$ ${\displaystyle V'}$

${\displaystyle {\text{ for all }}A\in {\mathcal {A}}\qquad \|\varphi _{i}-\varphi \|_{A}=\sup _{x\in A}|\varphi _{i}(x)-\varphi (x)|{\underset {i\to \infty }{\longrightarrow }}0.}$

Generalmente (pero no necesariamente) se supone que la clase satisface las siguientes condiciones: ${\displaystyle {\mathcal {A}}}$

• Cada punto de pertenece a algún conjunto : ${\displaystyle x}$ ${\displaystyle V}$ ${\displaystyle A\in {\mathcal {A}}}$

  ${\displaystyle {\text{ for all }}x\in V\quad {\text{ there exists some }}A\in {\mathcal {A}}\quad {\text{ such that }}x\in A.}$

• Cada dos conjuntos están contenidos en algún conjunto : ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle B\in {\mathcal {A}}}$ ${\displaystyle C\in {\mathcal {A}}}$

  ${\displaystyle {\text{ for all }}A,B\in {\mathcal {A}}\quad {\text{ there exists some }}C\in {\mathcal {A}}\quad {\text{ such that }}A\cup B\subseteq C.}$

• ${\displaystyle {\mathcal {A}}}$está cerrado bajo la operación de multiplicación por escalares:

  ${\displaystyle {\text{ for all }}A\in {\mathcal {A}}\quad {\text{ and all }}\lambda \in {\mathbb {F} }\quad {\text{ such that }}\lambda \cdot A\in {\mathcal {A}}.}$

Si se cumplen estos requisitos entonces la topología correspondiente es Hausdorff y los conjuntos ${\displaystyle V'}$

${\displaystyle U_{A}~=~\left\{\varphi \in V'~:~\quad \|\varphi \|_{A}<1\right\},\qquad {\text{ for }}A\in {\mathcal {A}}}$

formar su base local.

A continuación se presentan los tres casos especiales más importantes.

• La topología fuerte en es la topología de convergencia uniforme en subconjuntos acotados en (por lo que aquí puede elegirse como la clase de todos los subconjuntos acotados en ). ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle V}$

Si es un espacio vectorial normado (por ejemplo, un espacio de Banach o un espacio de Hilbert ), entonces la topología fuerte en está normada (de hecho, un espacio de Banach si el campo de escalares es completo), con la norma ${\displaystyle V}$ ${\displaystyle V'}$

${\displaystyle \|\varphi \|=\sup _{\|x\|\leq 1}|\varphi (x)|.}$

• La topología estereotipada en es la topología de convergencia uniforme en conjuntos totalmente acotados en (por lo que aquí puede elegirse como la clase de todos los subconjuntos totalmente acotados en ). ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle V}$
• La topología débil en es la topología de convergencia uniforme en subconjuntos finitos en (por lo que aquí puede elegirse como la clase de todos los subconjuntos finitos en ). ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle V}$

Cada una de estas tres opciones de topología conduce a una variante de la propiedad de reflexividad para espacios vectoriales topológicos: ${\displaystyle V'}$

• Si está dotado de la topología fuerte , entonces la noción correspondiente de reflexividad es la estándar: los espacios reflexivos en este sentido se denominan simplemente reflexivos . ^[18] ${\displaystyle V'}$
• Si está dotado de la topología dual estereotípica, entonces la reflexividad correspondiente se presenta en la teoría de espacios estereotípicos : los espacios reflexivos en este sentido se denominan estereotipos . ${\displaystyle V'}$
• Si está dotado de la topología débil , entonces la reflexividad correspondiente se presenta en la teoría de pares duales : ^[19] los espacios reflexivos en este sentido son espacios arbitrarios (Hausdorff) localmente convexos con la topología débil. ^[20] ${\displaystyle V'}$

Ejemplos

Sea 1 < p < ∞ un número real y considere el espacio de Banach ℓ  p de todas las secuencias a = ( a _n ) para las cuales

${\displaystyle \|\mathbf {a} \|_{p}=\left(\sum _{n=0}^{\infty }|a_{n}|^{p}\right)^{\frac {1}{p}}<\infty .}$

Definamos el número q por 1/ p + 1/ q = 1 . Entonces el dual continuo de ℓ ^p se identifica naturalmente con ℓ ^q : dado un elemento , el elemento correspondiente de ℓ ^q es la sucesión donde denota la sucesión cuyo término n -ésimo es 1 y todos los demás son cero. Por el contrario, dado un elemento a = ( a _n ) ∈ ℓ ^q , el funcional lineal continuo correspondiente en ℓ ^p se define por ${\displaystyle \varphi \in (\ell ^{p})'}$ ${\displaystyle (\varphi (\mathbf {e} _{n}))}$ ${\displaystyle \mathbf {e} _{n}}$ ${\displaystyle \varphi }$

${\displaystyle \varphi (\mathbf {b} )=\sum _{n}a_{n}b_{n}}$

para todo b = ( b _n ) ∈ ℓ ^p (véase la desigualdad de Hölder ).

De manera similar, el dual continuo de ℓ ¹ se identifica naturalmente con ℓ ^∞ (el espacio de sucesiones acotadas). Además, los duales continuos de los espacios de Banach c (que consisten en todas las sucesiones convergentes , con la norma suprema ) y c ₀ (las sucesiones que convergen a cero) se identifican ambos naturalmente con ℓ ¹ .

Según el teorema de representación de Riesz , el dual continuo de un espacio de Hilbert es a su vez un espacio de Hilbert antiisomorfo al espacio original. Esto da lugar a la notación bra-ket utilizada por los físicos en la formulación matemática de la mecánica cuántica .

Por el teorema de representación de Riesz-Markov-Kakutani , el dual continuo de ciertos espacios de funciones continuas puede describirse utilizando medidas.

Transposición de una función lineal continua

Si T  : V → W es una función lineal continua entre dos espacios vectoriales topológicos, entonces la transpuesta (continua) T′  : W′ → V′ se define mediante la misma fórmula que antes:

${\displaystyle T'(\varphi )=\varphi \circ T,\quad \varphi \in W'.}$

La función resultante T′ ( φ ) está en V′ . La asignación T → T′ produce una función lineal entre el espacio de funciones lineales continuas de V a W y el espacio de funciones lineales de W′ a V′ . Cuando T y U son funciones lineales continuas componibles, entonces

${\displaystyle (U\circ T)'=T'\circ U'.}$

Cuando V y W son espacios normados, la norma de la transpuesta en L ( W′ , V′ ) es igual a la de T en L ( V , W ) . Varias propiedades de la transposición dependen del teorema de Hahn-Banach . Por ejemplo, la función lineal acotada T tiene rango denso si y solo si la transpuesta T′ es inyectiva.

Cuando T es una función lineal compacta entre dos espacios de Banach V y W , entonces la transpuesta T′ es compacta. Esto se puede demostrar utilizando el teorema de Arzelà–Ascoli .

Cuando V es un espacio de Hilbert, existe un isomorfismo antilineal i _V de V sobre su dual continuo V′ . Para cada función lineal acotada T sobre V , los operadores transpuestos y adjuntos están vinculados por

${\displaystyle i_{V}\circ T^{*}=T'\circ i_{V}.}$

Cuando T es una función lineal continua entre dos espacios vectoriales topológicos V y W , entonces la transpuesta T′ es continua cuando W′ y V′ están equipados con topologías "compatibles": por ejemplo, cuando para X = V y X = W , ambos duales X′ tienen la topología fuerte β ( X′ , X ) de convergencia uniforme en conjuntos acotados de X , o ambos tienen la topología débil-∗ σ ( X′ , X ) de convergencia puntual en  X . La transpuesta T′ es continua de β ( W′ , W ) a β ( V′ , V ) , o de σ ( W′ , W ) a σ ( V′ , V ) .

Aniquiladores

Supongamos que W es un subespacio lineal cerrado de un espacio normado  V , y consideremos el aniquilador de W en V′ ,

${\displaystyle W^{\perp }=\{\varphi \in V':W\subseteq \ker \varphi \}.}$

Entonces, el dual del cociente V  /  W  puede identificarse con W ^⊥ , y el dual de W puede identificarse con el cociente V′  /  W ^⊥ . ^[21] En efecto, sea P la sobreyección canónica de V sobre el cociente V  /  W  ; entonces, la transpuesta P′ es un isomorfismo isométrico de ( V  /  W  )′ en V′ , con rango igual a W ^⊥ . Si j denota la función de inyección de W en V , entonces el núcleo de la transpuesta j′ es el aniquilador de W :

${\displaystyle \ker(j')=W^{\perp }}$

y se deduce del teorema de Hahn-Banach que j′ induce un isomorfismo isométrico V′  /  W ^⊥ → W′ .

Otras propiedades

Si el dual de un espacio normado V es separable , entonces también lo es el propio espacio V. Lo inverso no es cierto: por ejemplo, el espacio ℓ ¹ es separable, pero su dual ℓ ^∞ no lo es.

Doble dual

Esta es una transformación natural de la suma de vectores de un espacio vectorial a su doble dual. ⟨ x ₁ , x ₂ ⟩ denota el par ordenado de dos vectores. La suma + envía x ₁ y x ₂ a x ₁ + x ₂ . La suma +′ inducida por la transformación se puede definir como para cualquier en el espacio dual. ${\displaystyle [\Psi (x_{1})+'\Psi (x_{2})](\varphi )=\varphi (x_{1}+x_{2})=\varphi (x)}$ ${\displaystyle \varphi }$

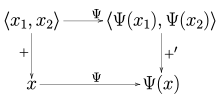
En analogía con el caso del doble dual algebraico, siempre hay un operador lineal continuo naturalmente definido Ψ : V → V′′ desde un espacio normado V en su doble dual continuo V′′ , definido por

${\displaystyle \Psi (x)(\varphi )=\varphi (x),\quad x\in V,\ \varphi \in V'.}$

Como consecuencia del teorema de Hahn-Banach , esta función es de hecho una isometría , lo que significa que ‖ Ψ( x ) ‖ = ‖ x ‖ para todo x ∈ V . Los espacios normados para los cuales la función Ψ es una biyección se denominan reflexivos .

Cuando V es un espacio vectorial topológico , entonces Ψ( x ) puede definirse con la misma fórmula, para cada x ∈ V , sin embargo surgen varias dificultades. Primero, cuando V no es localmente convexo , el dual continuo puede ser igual a { 0 } y la función Ψ trivial. Sin embargo, si V es Hausdorff y localmente convexo, la función Ψ es inyectiva desde V al dual algebraico V′ ^∗ del dual continuo, nuevamente como consecuencia del teorema de Hahn-Banach. ^{[nb 5]}

En segundo lugar, incluso en el entorno localmente convexo, se pueden definir varias topologías de espacio vectorial natural en el dual continuo V′ , de modo que el doble dual continuo V′′ no se define de forma única como un conjunto. Decir que Ψ se asigna de V a V′′ , o en otras palabras, que Ψ( x ) es continuo en V′ para cada x ∈ V , es un requisito mínimo razonable en la topología de V′ , es decir, que las asignaciones de evaluación

${\displaystyle \varphi \in V'\mapsto \varphi (x),\quad x\in V,}$

ser continua para la topología elegida en V′ . Además, todavía existe una elección de una topología en V′� , y la continuidad de Ψ depende de esta elección. En consecuencia, definir la reflexividad en este marco es más complejo que en el caso normalizado.

Véase también

• Covarianza y contravarianza de vectores
• Módulo dual
• Doble norma
• Dualidad (matemáticas)
• Dualidad (geometría proyectiva)
• Dualidad de Pontryagin
• Red recíproca : base espacial dual en cristalografía

Notas

1. Para su uso de esta manera, véase Introducción a las variedades (Tu 2011, p. 19). Esta notación se utiliza a veces cuando se reserva para algún otro significado. Por ejemplo, en el texto anterior, se utiliza con frecuencia para denotar el codiferencial de , de modo que representa el pullback de la forma . Halmos (1974, p. 20) utiliza para denotar el dual algebraico de . Sin embargo, otros autores utilizan para el dual continuo, mientras que reservan para el dual algebraico (Trèves 2006, p. 35). ${\displaystyle V^{\lor }}$ ${\displaystyle (\cdot )^{*}}$ ${\displaystyle F^{*}}$ ${\displaystyle F}$ ${\displaystyle F^{*}\omega }$ ${\displaystyle \omega }$ ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle V'}$ ${\displaystyle V^{*}}$
2. En muchas áreas, como la mecánica cuántica , ⟨·,·⟩ se reserva para una forma sesquilínea definida en V × V .
3. Varias afirmaciones de este artículo requieren el axioma de elección para su justificación. El axioma de elección es necesario para demostrar que un espacio vectorial arbitrario tiene una base: en particular, es necesario para demostrar que tiene una base. También es necesario para demostrar que el dual de un espacio vectorial de dimensión infinita es distinto de cero y, por lo tanto, que la función natural de a su doble dual es inyectiva. ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ ${\displaystyle V}$ ${\displaystyle V}$
4. Para ser precisos, el análisis de Fourier continuo estudia el espacio de funcionales con dominio un espacio vectorial y el espacio de funcionales en el espacio vectorial dual.
5. Si V es localmente convexo pero no de Hausdorff, el núcleo de Ψ es el subespacio cerrado más pequeño que contiene a {0}.

Referencias

1. Narici y Beckenstein 2011, págs. 225–273.
2. Katznelson y Katznelson (2008) pág. 37, §2.1.3
3. Tu (2011) pág. 19, §3.1
4. Axler (2015) pág. 101, §3.94
5. Halmos (1974) pág. 20, §13
6. Halmos (1974) pág. 21, §14
7. Misner, Thorne y Wheeler 1973
8. Misner, Thorne y Wheeler 1973, §2.5
9. Nicolas Bourbaki (1974). Hermann (ed.). Elementos de matemáticas: Álgebra I, capítulos 1-3 . pág. 400. ISBN 0201006391.
10. Mac Lane y Birkhoff 1999, §VI.4
11. Halmos (1974) págs. 25, 28
12. Halmos (1974) §44
13. Tao, Terence (29 de diciembre de 2012). "Una formalización matemática del análisis dimensional". De manera similar, se puede definir como el espacio dual ... ${\displaystyle V^{T^{-1}}}$ ${\displaystyle V^{T}}$
14. Robertson y Robertson 1964, II.2
15. Schaefer 1966, II.4
16. Rudin 1973, 3.1
17. Bourbaki 2003, II.42
18. Schaefer 1966, IV.5.5
19. Schaefer 1966, IV.1
20. Schaefer 1966, IV.1.2
21. Rudin 1991, capítulo 4

Bibliografía

• Axler, Sheldon Jay (2015). Álgebra lineal bien hecha (3.ª ed.). Springer . ISBN 978-3-319-11079-0.
• Bourbaki, Nicolas (1989). Elementos de matemáticas, Álgebra I. Springer-Verlag. ISBN 3-540-64243-9.
• Bourbaki, Nicolas (2003). Elementos de matemáticas, Espacios vectoriales topológicos . Springer-Verlag.
• Halmos, Paul Richard (1974) [1958]. Espacios vectoriales de dimensión finita (2.ª ed.). Springer . ISBN 0-387-90093-4.
• Katznelson, Yitzhak ; Katznelson, Yonatan R. (2008). Una introducción (concisa) al álgebra lineal . Sociedad Matemática Estadounidense . ISBN 978-0-8218-4419-9.
• Lang, Serge (2002), Álgebra , Textos de posgrado en matemáticas , vol. 211 (tercera edición revisada), Nueva York: Springer-Verlag, ISBN 978-0-387-95385-4, MR  1878556, Zbl  0984.00001
• Tu, Loring W. (2011). Introducción a las variedades (2.ª ed.). Springer . ISBN 978-1-4419-7400-6.
• Mac Lane, Saunders ; Birkhoff, Garrett (1999). Álgebra (3.ª ed.). AMS Chelsea Publishing. ISBN 0-8218-1646-2..
• Misner, Charles W .; Thorne, Kip S .; Wheeler, John A. (1973). Gravitación . WH Freeman. ISBN 0-7167-0344-0.
• Narici, Lawrence; Beckenstein, Edward (2011). Espacios vectoriales topológicos . Matemáticas puras y aplicadas (segunda edición). Boca Raton, FL: CRC Press. ISBN 978-1584888666.OCLC 144216834  .
• Rudin, Walter (1973). Análisis funcional . Serie internacional de matemáticas puras y aplicadas. Vol. 25 (primera edición). Nueva York, NY: McGraw-Hill Science/Engineering/Math . ISBN 9780070542259.
• Rudin, Walter (1991). Análisis funcional. Serie internacional de matemáticas puras y aplicadas. Vol. 8 (segunda edición). Nueva York, NY: McGraw-Hill Science/Engineering/Math . ISBN 978-0-07-054236-5.OCLC 21163277  .
• Robertson, AP; Robertson, W. (1964). Espacios vectoriales topológicos . Cambridge University Press.
• Schaefer, Helmut H. (1966). Espacios vectoriales topológicos . Nueva York: The Macmillan Company.
• Schaefer, Helmut H. ; Wolff, Manfred P. (1999). Espacios vectoriales topológicos . GTM . Vol. 8 (Segunda ed.). Nueva York, NY: Springer New York Imprenta Springer. ISBN 978-1-4612-7155-0.OCLC 840278135  .
• Trèves, François (2006) [1967]. Espacios vectoriales topológicos, distribuciones y núcleos . Mineola, Nueva York: Publicaciones de Dover. ISBN 978-0-486-45352-1.OCLC 853623322  .

Enlaces externos

• Weisstein, Eric W. "Espacio vectorial dual". MathWorld .