Vector de Laplace-Runge-Lenz

Vector utilizado en astronomía

En mecánica clásica , el vector Laplace-Runge-Lenz (LRL) es un vector utilizado principalmente para describir la forma y orientación de la órbita de un cuerpo astronómico alrededor de otro, como una estrella binaria o un planeta que gira alrededor de una estrella. Para dos cuerpos que interactúan por gravedad newtoniana , el vector LRL es una constante de movimiento , lo que significa que es el mismo sin importar dónde se calcule en la órbita; ^{[1] [2]} equivalentemente, se dice que el vector LRL se conserva . De manera más general, el vector LRL se conserva en todos los problemas en los que dos cuerpos interactúan por una fuerza central que varía como el cuadrado inverso de la distancia entre ellos; tales problemas se denominan problemas de Kepler . ^{[3] [4] [5] [6]}

El átomo de hidrógeno es un problema de Kepler, ya que comprende dos partículas cargadas que interactúan mediante la ley de electrostática de Coulomb , otra fuerza central de inverso del cuadrado. El vector LRL fue esencial en la primera derivación mecánica cuántica del espectro del átomo de hidrógeno, ^{[7] [8]} antes del desarrollo de la ecuación de Schrödinger . Sin embargo, este enfoque rara vez se utiliza en la actualidad.

En mecánica clásica y cuántica, las cantidades conservadas generalmente corresponden a una simetría del sistema. ^[9] La conservación del vector LRL corresponde a una simetría inusual; el problema de Kepler es matemáticamente equivalente a una partícula que se mueve libremente en la superficie de una (hiper)esfera de cuatro dimensiones , ^[10] de modo que todo el problema es simétrico bajo ciertas rotaciones del espacio de cuatro dimensiones. ^[11] Esta mayor simetría resulta de dos propiedades del problema de Kepler: el vector de velocidad siempre se mueve en un círculo perfecto y, para una energía total dada , todos esos círculos de velocidad se intersecan entre sí en los mismos dos puntos. ^[12]

El vector de Laplace-Runge-Lenz debe su nombre a Pierre-Simon de Laplace , Carl Runge y Wilhelm Lenz . También se lo conoce como vector de Laplace , ^{[13] [14]} vector de Runge-Lenz ^[15] y vector de Lenz . ^[8] Irónicamente, ninguno de esos científicos lo descubrió. ^[15] El vector LRL ha sido redescubierto y reformulado varias veces; ^[15] por ejemplo, es equivalente al vector de excentricidad adimensional de la mecánica celeste . ^{[2] [14] [16]} Se han definido varias generalizaciones del vector LRL, que incorporan los efectos de la relatividad especial , los campos electromagnéticos e incluso diferentes tipos de fuerzas centrales. ^{[17] [18] [19]}

Contexto

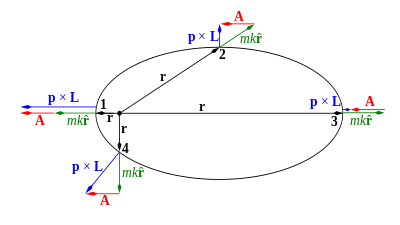
Una sola partícula que se mueve bajo cualquier fuerza central conservativa tiene al menos cuatro constantes de movimiento: la energía total E y los tres componentes cartesianos del vector de momento angular L con respecto al centro de fuerza. ^{[20] [21]} La órbita de la partícula está confinada al plano definido por el momento inicial de la partícula p (o, equivalentemente, su velocidad v ) y el vector r entre la partícula y el centro de fuerza ^{[20] [21]} (véase la Figura 1). Este plano de movimiento es perpendicular al vector de momento angular constante L = r × p ; esto puede expresarse matemáticamente mediante la ecuación del producto escalar vectorial r ⋅ L = 0 . Dada su definición matemática a continuación, el vector de Laplace–Runge–Lenz (vector LRL) A siempre es perpendicular al vector de momento angular constante L para todas las fuerzas centrales ( A ⋅ L = 0 ). Por lo tanto, A siempre se encuentra en el plano de movimiento. Como se muestra a continuación, A apunta desde el centro de fuerza hasta el periapsis del movimiento, el punto de aproximación más cercano, y su longitud es proporcional a la excentricidad de la órbita. ^[1]

El vector LRL A ​​es constante en longitud y dirección, pero solo para una fuerza central de ley inversa del cuadrado. ^[1] Para otras fuerzas centrales , el vector A no es constante, sino que cambia tanto en longitud como en dirección. Si la fuerza central es aproximadamente una ley inversa del cuadrado, el vector A es aproximadamente constante en longitud, pero gira lentamente su dirección. ^[14] Se puede definir un vector LRL conservado generalizado para todas las fuerzas centrales, pero este vector generalizado es una función complicada de la posición y, por lo general, no se puede expresar en forma cerrada . ^{[18] [19]} ${\displaystyle {\mathcal {A}}}$

El vector LRL se diferencia de otras magnitudes conservadas en la siguiente propiedad. Mientras que para las magnitudes conservadas típicas existe una coordenada cíclica correspondiente en el lagrangiano tridimensional del sistema, no existe tal coordenada para el vector LRL. Por lo tanto, la conservación del vector LRL debe deducirse directamente, por ejemplo, mediante el método de los corchetes de Poisson , como se describe a continuación. Las magnitudes conservadas de este tipo se denominan "dinámicas", en contraste con las leyes de conservación "geométricas" habituales, por ejemplo, la del momento angular.

Historia del redescubrimiento

El vector LRL A ​​es una constante de movimiento del problema de Kepler y resulta útil para describir órbitas astronómicas, como el movimiento de planetas y estrellas binarias. Sin embargo, nunca ha sido muy conocido entre los físicos, posiblemente porque es menos intuitivo que el momento y el momento angular. En consecuencia, ha sido redescubierto de forma independiente varias veces a lo largo de los últimos tres siglos. ^[15]

Jakob Hermann fue el primero en demostrar que A se conserva para un caso especial de la fuerza central de la inversa del cuadrado, ^[22] y calculó su conexión con la excentricidad de la elipse orbital . El trabajo de Hermann fue generalizado a su forma moderna por Johann Bernoulli en 1710. ^[23] A finales de siglo, Pierre-Simon de Laplace redescubrió la conservación de A , derivándola analíticamente, en lugar de geométricamente. ^[24] A mediados del siglo XIX, William Rowan Hamilton derivó el vector de excentricidad equivalente definido a continuación, ^[16] usándolo para demostrar que el vector de momento p se mueve en un círculo para el movimiento bajo una fuerza central de la inversa del cuadrado (Figura 3). ^[12]

A principios del siglo XX, Josiah Willard Gibbs derivó el mismo vector mediante análisis vectorial . ^[25] La derivación de Gibbs fue utilizada como ejemplo por Carl Runge en un popular libro de texto alemán sobre vectores, ^[26] al que Wilhelm Lenz hizo referencia en su artículo sobre el (antiguo) tratamiento mecánico cuántico del átomo de hidrógeno. ^[27] En 1926, Wolfgang Pauli utilizó el vector LRL para derivar los niveles de energía del átomo de hidrógeno utilizando la formulación de mecánica matricial de la mecánica cuántica, ^[7] después de lo cual se conoció principalmente como el vector de Runge-Lenz . ^[15]

Definición matemática

Una fuerza central de cuadrado inverso que actúa sobre una sola partícula se describe mediante la ecuación La energía potencial correspondiente está dada por . El parámetro constante k describe la intensidad de la fuerza central; es igual a G ⋅ M ⋅ m para fuerzas gravitacionales y − k e ⋅ Q ⋅ q para fuerzas electrostáticas. La fuerza es atractiva si k > 0 y repulsiva si k < 0 . $${\displaystyle \mathbf {F} (r)=-{\frac {k}{r^{2}}}\mathbf {\hat {r}} ;}$$ ${\displaystyle V(r)=-k/r}$

Figura 1: El vector LRL A ​​(mostrado en rojo) en cuatro puntos (etiquetados 1, 2, 3 y 4) en la órbita elíptica de una partícula puntual ligada que se mueve bajo una fuerza central de cuadrado inverso. El centro de atracción se muestra como un pequeño círculo negro desde el cual emanan los vectores de posición (también negros). El vector de momento angular L es perpendicular a la órbita. Los vectores coplanares p × L y ( mk / r ) r se muestran en azul y verde, respectivamente; estas variables se definen a continuación. El vector A es constante en dirección y magnitud.

El vector LRL A ​​se define matemáticamente mediante la fórmula ^[1]

${\displaystyle \mathbf {A} =\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}} ,}$

dónde

• m es la masa de la partícula puntual que se mueve bajo la fuerza central,
• p es su vector de momento,
• L = r × p es su vector de momento angular,
• r es el vector de posición de la partícula (Figura 1),
• ${\displaystyle \mathbf {\hat {r}} }$es el vector unitario correspondiente , es decir , y ${\displaystyle \mathbf {\hat {r}} ={\frac {\mathbf {r} }{r}}}$
• r es la magnitud de r , la distancia de la masa desde el centro de fuerza.

Las unidades del SI del vector LRL son julio-kilogramo-metro (J⋅kg⋅m). Esto se debe a que las unidades de p y L son kg⋅m/s y J⋅s, respectivamente. Esto concuerda con las unidades de m (kg) y de k (N⋅m ² ).

Esta definición del vector LRL A ​​se refiere a una partícula puntual de masa m que se mueve bajo la acción de una fuerza fija. Sin embargo, la misma definición puede extenderse a problemas de dos cuerpos , como el problema de Kepler, tomando m como la masa reducida de los dos cuerpos y r como el vector entre los dos cuerpos.

Dado que la fuerza supuesta es conservativa, la energía total E es una constante de movimiento, $${\displaystyle E={\frac {p^{2}}{2m}}-{\frac {k}{r}}={\frac {1}{2}}mv^{2}-{\frac {k}{r}}.}$$

La fuerza supuesta también es una fuerza central. Por lo tanto, el vector de momento angular L también se conserva y define el plano en el que se desplaza la partícula. El vector LRL A ​​es perpendicular al vector de momento angular L porque tanto p × L como r son perpendiculares a L . De ello se deduce que A se encuentra en el plano de movimiento.

Se pueden definir formulaciones alternativas para la misma constante de movimiento, típicamente escalando el vector con constantes, como la masa m , el parámetro de fuerza k o el momento angular L . ^[15] La variante más común es dividir A por mk , lo que produce el vector de excentricidad, ^{[2] [16]} un vector adimensional a lo largo del semieje mayor cuyo módulo es igual a la excentricidad de la cónica: Una formulación equivalente ^[14] multiplica este vector de excentricidad por el semieje mayor a , dando al vector resultante las unidades de longitud. Otra formulación ^[28] divide A por , produciendo una cantidad conservada equivalente con unidades de longitud inversa, una cantidad que aparece en la solución del problema de Kepler donde es el ángulo entre A y el vector de posición r . A continuación se dan formulaciones alternativas adicionales. $${\displaystyle \mathbf {e} ={\frac {\mathbf {A} }{mk}}={\frac {1}{mk}}(\mathbf {p} \times \mathbf {L} )-\mathbf {\hat {r}} .}$$ ${\displaystyle L^{2}}$ $${\displaystyle u\equiv {\frac {1}{r}}={\frac {km}{L^{2}}}+{\frac {A}{L^{2}}}\cos \theta }$$ ${\displaystyle \theta }$

Derivación de las órbitas de Kepler

Figura 2: Versión simplificada de la Figura 1, que define el ángulo θ entre A y r en un punto de la órbita.

La forma y orientación de las órbitas se pueden determinar a partir del vector LRL de la siguiente manera. ^[1] Tomando el producto escalar de A con el vector de posición r se obtiene la ecuación donde θ es el ángulo entre r y A (Figura 2). Permutando el triple producto escalar se obtiene $${\displaystyle \mathbf {A} \cdot \mathbf {r} =A\cdot r\cdot \cos \theta =\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)-mkr,}$$ $${\displaystyle \mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \right)=\left(\mathbf {r} \times \mathbf {p} \right)\cdot \mathbf {L} =\mathbf {L} \cdot \mathbf {L} =L^{2}}$$

Al reorganizar se obtiene la solución de la ecuación de Kepler.

${\displaystyle {\frac {1}{r}}={\frac {mk}{L^{2}}}+{\frac {A}{L^{2}}}\cos \theta }$

Esto corresponde a la fórmula para una sección cónica de excentricidad e donde la excentricidad y C es una constante. ^[1] $${\displaystyle {\frac {1}{r}}=C\cdot \left(1+e\cdot \cos \theta \right)}$$ ${\displaystyle e={\frac {A}{\left|mk\right|}}\geq 0}$

Tomando el producto escalar de A consigo mismo se obtiene una ecuación que involucra la energía total E , ^[1] que puede reescribirse en términos de la excentricidad, ^[1] $${\displaystyle A^{2}=m^{2}k^{2}+2mEL^{2},}$$ $${\displaystyle e^{2}=1+{\frac {2L^{2}}{mk^{2}}}E.}$$

Así, si la energía E es negativa (órbitas ligadas), la excentricidad es menor que uno y la órbita es una elipse. Por el contrario, si la energía es positiva (órbitas no ligadas, también llamadas "órbitas dispersas" ^[1] ), la excentricidad es mayor que uno y la órbita es una hipérbola . ^[1] Finalmente, si la energía es exactamente cero, la excentricidad es uno y la órbita es una parábola . ^[1] En todos los casos, la dirección de A se encuentra a lo largo del eje de simetría de la sección cónica y apunta desde el centro de fuerza hacia el periapsis, el punto de aproximación más cercano. ^[1]

Hodógrafas de momento circular

Figura 3: El vector de momento p (mostrado en azul) se mueve en un círculo mientras la partícula se mueve en una elipse. Los cuatro puntos etiquetados corresponden a los de la Figura 1. El círculo está centrado en el eje y en la posición A / L (mostrado en magenta), con radio mk / L (mostrado en verde). El ángulo η determina la excentricidad e de la órbita elíptica ( cos η = e ). Por el teorema del ángulo inscrito para círculos , η es también el ángulo entre cualquier punto del círculo y los dos puntos de intersección con el eje p _x , p _x = ± p ₀ , que solo dependen de E , pero no de L .

La conservación del vector LRL A ​​y del vector de momento angular L es útil para demostrar que el vector de momento p se mueve en un círculo bajo una fuerza central de inverso del cuadrado. ^{[12] [15]}

Tomando el producto escalar de consigo mismo se obtiene $${\displaystyle mk{\hat {\mathbf {r} }}=\mathbf {p} \times \mathbf {L} -\mathbf {A} }$$ $${\displaystyle (mk)^{2}=A^{2}+p^{2}L^{2}+2\mathbf {L} \cdot (\mathbf {p} \times \mathbf {A} ).}$$

Además, al elegir L a lo largo del eje z y el semieje mayor como el eje x , se obtiene la ecuación del lugar geométrico para p ,

${\displaystyle p_{x}^{2}+\left(p_{y}-{\frac {A}{L}}\right)^{2}=\left({\frac {mk}{L}}\right)^{2}.}$

En otras palabras, el vector de momento p está confinado a un círculo de radio mk / L = L / ℓ centrado en (0, A / L ) . ^[29] Para órbitas acotadas, la excentricidad e corresponde al coseno del ángulo η que se muestra en la Figura 3. Para órbitas no acotadas, tenemos y por lo tanto el círculo no interseca el eje . ${\displaystyle A>mk}$ ${\displaystyle p_{x}}$

En el límite degenerado de las órbitas circulares, y por tanto nula A , el círculo se centra en el origen (0,0) . Por brevedad, también es útil introducir la variable . ${\textstyle p_{0}={\sqrt {2m|E|}}}$

Esta hodógrafa circular es útil para ilustrar la simetría del problema de Kepler.

Constantes de movimiento y superintegrabilidad

Las siete cantidades escalares E , A y L (al ser vectores, las dos últimas contribuyen con tres cantidades conservadas cada una) están relacionadas por dos ecuaciones, A ⋅ L = 0 y A ² = m ² k ² + 2 mEL ² , dando cinco constantes de movimiento independientes . (Dado que la magnitud de A , y por lo tanto la excentricidad e de la órbita, se puede determinar a partir del momento angular total L y la energía E , solo la dirección de A se conserva independientemente; además, dado que A debe ser perpendicular a L , contribuye solo con una cantidad conservada adicional).

Esto es coherente con las seis condiciones iniciales (los vectores de posición y velocidad iniciales de la partícula, cada uno con tres componentes) que especifican la órbita de la partícula, ya que el tiempo inicial no está determinado por una constante de movimiento. La órbita unidimensional resultante en un espacio de fases de seis dimensiones está, por tanto, completamente especificada.

Un sistema mecánico con d grados de libertad puede tener como máximo 2 d − 1 constantes de movimiento, ya que hay 2 d condiciones iniciales y el tiempo inicial no puede determinarse por una constante de movimiento. Un sistema con más de d constantes de movimiento se denomina superintegrable y un sistema con 2 d − 1 constantes se denomina máximamente superintegrable . ^[30] Dado que la solución de la ecuación de Hamilton-Jacobi en un sistema de coordenadas puede producir solo d constantes de movimiento, los sistemas superintegrables deben ser separables en más de un sistema de coordenadas. ^[31] El problema de Kepler es máximamente superintegrable, ya que tiene tres grados de libertad ( d = 3 ) y cinco constantes de movimiento independientes; su ecuación de Hamilton-Jacobi es separable tanto en coordenadas esféricas como en coordenadas parabólicas , ^[17] como se describe a continuación.

Los sistemas máximamente superintegrables siguen órbitas cerradas y unidimensionales en el espacio de fases , ya que la órbita es la intersección de las isosuperficies del espacio de fases de sus constantes de movimiento. En consecuencia, las órbitas son perpendiculares a todos los gradientes de todas estas isosuperficies independientes, cinco en este problema específico, y por lo tanto están determinadas por los productos cruzados generalizados de todos estos gradientes. Como resultado, todos los sistemas superintegrables son automáticamente descriptibles por la mecánica de Nambu , ^[32] alternativamente y de manera equivalente, por la mecánica hamiltoniana .

Los sistemas máximamente superintegrables se pueden cuantificar utilizando relaciones de conmutación , como se ilustra a continuación. ^[33] Sin embargo, de manera equivalente, también se cuantifican en el marco de Nambu, como este problema clásico de Kepler en el átomo de hidrógeno cuántico. ^[34]

Evolución bajo potenciales perturbados

Figura 5: Órbita elíptica con precesión gradual, con una excentricidad e  = 0,667. Dicha precesión surge en el problema de Kepler si la fuerza central de atracción se desvía ligeramente de una ley de la inversa del cuadrado. La tasa de precesión se puede calcular utilizando las fórmulas del texto.

El vector A de Laplace-Runge-Lenz se conserva solo para una fuerza central perfecta de inverso del cuadrado. Sin embargo, en la mayoría de los problemas prácticos, como el movimiento planetario, la energía potencial de interacción entre dos cuerpos no es exactamente una ley de inverso del cuadrado, sino que puede incluir una fuerza central adicional, una denominada perturbación descrita por una energía potencial h ( r ) . En tales casos, el vector LRL gira lentamente en el plano de la órbita, lo que corresponde a una precesión apsidal lenta de la órbita.

Por suposición, el potencial perturbador h ( r ) es una fuerza central conservativa, lo que implica que la energía total E y el vector de momento angular L se conservan. Por lo tanto, el movimiento todavía se encuentra en un plano perpendicular a L y la magnitud A se conserva, a partir de la ecuación A ² = m ² k ² + 2 mEL ² . El potencial perturbador h ( r ) puede ser cualquier tipo de función, pero debería ser significativamente más débil que la fuerza principal inversa del cuadrado entre los dos cuerpos.

La velocidad a la que gira el vector LRL proporciona información sobre el potencial perturbador h ( r ) . Utilizando la teoría de perturbación canónica y las coordenadas del ángulo de acción , es sencillo demostrar ^[1] que A gira a una velocidad de, donde T es el período orbital, y la identidad L dt = m r ² dθ se utilizó para convertir la integral de tiempo en una integral angular (Figura 5). La expresión entre corchetes angulares, ⟨ h ( r )⟩ , representa el potencial perturbador, pero promediado sobre un período completo; es decir, promediado sobre un paso completo del cuerpo alrededor de su órbita. Matemáticamente, este promedio de tiempo corresponde a la siguiente cantidad entre llaves. Este promedio ayuda a suprimir las fluctuaciones en la velocidad de rotación. $${\displaystyle {\begin{aligned}{\frac {\partial }{\partial L}}\langle h(r)\rangle &={\frac {\partial }{\partial L}}\left\{{\frac {1}{T}}\int _{0}^{T}h(r)\,dt\right\}\\[1em]&={\frac {\partial }{\partial L}}\left\{{\frac {m}{L^{2}}}\int _{0}^{2\pi }r^{2}h(r)\,d\theta \right\},\end{aligned}}}$$

Este enfoque se utilizó para ayudar a verificar la teoría de la relatividad general de Einstein , que agrega una pequeña perturbación cúbica inversa efectiva al potencial gravitacional normal de Newton, ^[35] $${\displaystyle h(r)={\frac {kL^{2}}{m^{2}c^{2}}}\left({\frac {1}{r^{3}}}\right).}$$

Insertando esta función en la integral y usando la ecuación para expresar r en términos de θ , se calcula que la tasa de precesión del periapsis causada por esta perturbación no newtoniana es ^[35] que coincide estrechamente con la precesión anómala observada de Mercurio ^{[36] y} los púlsares binarios . ^[37] Esta concordancia con el experimento es una evidencia sólida de la relatividad general. ^{[38] [39]} $${\displaystyle {\frac {1}{r}}={\frac {mk}{L^{2}}}\left(1+{\frac {A}{mk}}\cos \theta \right)}$$ $${\displaystyle {\frac {6\pi k^{2}}{TL^{2}c^{2}}},}$$

Corchetes de Poisson

Las funciones sin escalar

La estructura algebraica del problema es, como se explica en secciones posteriores, SO(4)/ Z ₂ ~ SO(3) × SO(3) . ^[11] Los tres componentes L _i del vector de momento angular L tienen los corchetes de Poisson ^[1] donde i = 1, 2, 3 y ε _ijs es el tensor completamente antisimétrico , es decir, el símbolo de Levi-Civita ; el índice de suma s se utiliza aquí para evitar confusiones con el parámetro de fuerza k definido anteriormente. Entonces, dado que el vector LRL A ​​se transforma como un vector, tenemos las siguientes relaciones de corchetes de Poisson entre A y L : ^[40] Finalmente, las relaciones de corchetes de Poisson entre los diferentes componentes de A son las siguientes: ^[41] donde es el hamiltoniano. Nótese que el lapso de los componentes de A y los componentes de L no está cerrado bajo corchetes de Poisson, debido al factor de en el lado derecho de esta última relación. $${\displaystyle \{L_{i},L_{j}\}=\sum _{s=1}^{3}\varepsilon _{ijs}L_{s},}$$ $${\displaystyle \{A_{i},L_{j}\}=\sum _{s=1}^{3}\varepsilon _{ijs}A_{s}.}$$ $${\displaystyle \{A_{i},A_{j}\}=-2mH\sum _{s=1}^{3}\varepsilon _{ijs}L_{s},}$$ ${\displaystyle H}$ ${\displaystyle H}$

Finalmente, dado que tanto L como A son constantes de movimiento, tenemos $${\displaystyle \{A_{i},H\}=\{L_{i},H\}=0.}$$

Los corchetes de Poisson se extenderán a las relaciones de conmutación mecánica cuántica en la siguiente sección y a los corchetes de Lie en una sección posterior.

Las funciones escaladas

Como se indica a continuación, un vector de Laplace-Runge-Lenz escalado D puede definirse con las mismas unidades que el momento angular dividiendo A por . Dado que D todavía se transforma como un vector, los corchetes de Poisson de D con el vector de momento angular L pueden escribirse de forma similar ^{[11] [8]} ${\textstyle p_{0}={\sqrt {2m|H|}}}$ $${\displaystyle \{D_{i},L_{j}\}=\sum _{s=1}^{3}\varepsilon _{ijs}D_{s}.}$$

Los corchetes de Poisson de D consigo mismo dependen del signo de H , es decir, de si la energía es negativa (que produce órbitas elípticas cerradas bajo una fuerza central de cuadrado inverso) o positiva (que produce órbitas hiperbólicas abiertas bajo una fuerza central de cuadrado inverso). Para energías negativas (es decir, para sistemas ligados), los corchetes de Poisson son ^[42] Ahora podemos apreciar la motivación para la escala elegida de D : con esta escala, el hamiltoniano ya no aparece en el lado derecho de la relación precedente. Por lo tanto, el lapso de los tres componentes de L y los tres componentes de D forman un álgebra de Lie de seis dimensiones bajo el corchete de Poisson. Esta álgebra de Lie es isomorfa a so(4) , el álgebra de Lie del grupo de rotación de cuatro dimensiones SO(4) . ^[43] $${\displaystyle \{D_{i},D_{j}\}=\sum _{s=1}^{3}\varepsilon _{ijs}L_{s}.}$$

Por el contrario, para la energía positiva , los corchetes de Poisson tienen el signo opuesto. En este caso, el álgebra de Lie es isomorfa a so(3,1) . $${\displaystyle \{D_{i},D_{j}\}=-\sum _{s=1}^{3}\varepsilon _{ijs}L_{s}.}$$

La distinción entre energías positivas y negativas surge porque el escalamiento deseado (el que elimina el hamiltoniano del lado derecho de las relaciones de corchete de Poisson entre los componentes del vector LRL escalado) involucra la raíz cuadrada del hamiltoniano. Para obtener funciones de valor real, debemos tomar el valor absoluto del hamiltoniano, que distingue entre valores positivos (donde ) y valores negativos (donde ). ${\displaystyle |H|=H}$ ${\displaystyle |H|=-H}$

Operador de Laplace-Runge-Lenz para el átomo de hidrógeno en el espacio de momento

El operador de Laplace-Runge-Lenz escalado en el espacio de momento se encontró en 2022. ^{[44] [45]} La fórmula para el operador es más simple que en el espacio de posición:

${\displaystyle {\hat {\mathbf {A} }}_{\mathbf {p} }=\imath ({\hat {l}}_{\mathbf {p} }+1)\mathbf {p} -{\frac {(p^{2}+1)}{2}}\imath \mathbf {\nabla } _{\mathbf {p} },}$

donde el "operador de grado"

${\displaystyle {\hat {l}}_{\mathbf {p} }=(\mathbf {p} \mathbf {\nabla } _{\mathbf {p} })}$

multiplica un polinomio homogéneo por su grado.

Invariantes de Casimir y niveles de energía

Los invariantes de Casimir para energías negativas son $${\displaystyle {\begin{aligned}C_{1}&=\mathbf {D} \cdot \mathbf {D} +\mathbf {L} \cdot \mathbf {L} ={\frac {mk^{2}}{2|E|}},\\C_{2}&=\mathbf {D} \cdot \mathbf {L} =0,\end{aligned}}}$$

y tienen corchetes de Poisson que se desvanecen con todos los componentes de D y L , C ₂ es trivialmente cero, ya que los dos vectores son siempre perpendiculares. $${\displaystyle \{C_{1},L_{i}\}=\{C_{1},D_{i}\}=\{C_{2},L_{i}\}=\{C_{2},D_{i}\}=0.}$$

Sin embargo, el otro invariante, C ₁ , no es trivial y depende solo de m , k y E . Tras la cuantificación canónica, este invariante permite derivar los niveles de energía de los átomos similares al hidrógeno utilizando únicamente relaciones de conmutación canónicas mecánicas cuánticas, en lugar de la solución convencional de la ecuación de Schrödinger. ^{[8] [43]} Esta derivación se analiza en detalle en la siguiente sección.

Mecánica cuántica del átomo de hidrógeno

Figura 6: Niveles de energía del átomo de hidrógeno predichos a partir de las relaciones de conmutación del momento angular y los operadores vectoriales de Laplace-Runge-Lenz; estos niveles de energía han sido verificados experimentalmente.

Los corchetes de Poisson proporcionan una guía simple para cuantificar la mayoría de los sistemas clásicos: la relación de conmutación de dos operadores mecánicos cuánticos se especifica mediante el corchete de Poisson de las variables clásicas correspondientes, multiplicado por iħ . ^[46]

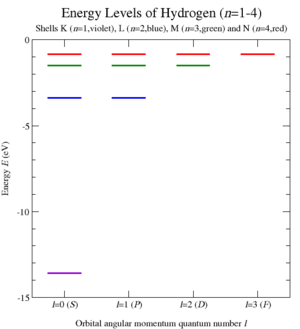
Al llevar a cabo esta cuantificación y calcular los valores propios del operador de Casimir C ₁ para el problema de Kepler, Wolfgang Pauli pudo derivar los niveles de energía de los átomos similares al hidrógeno (Figura 6) y, por lo tanto, su espectro de emisión atómica. ^[7] Esta elegante derivación de 1926 se obtuvo antes del desarrollo de la ecuación de Schrödinger . ^[47]

Una sutileza del operador mecánico cuántico para el vector LRL A ​​es que los operadores de momento y momento angular no conmutan; por lo tanto, el producto vectorial del operador cuántico de p y L debe definirse cuidadosamente. ^[8] Normalmente, los operadores para los componentes cartesianos A _s se definen utilizando un producto simetrizado (hermítico). Una vez hecho esto, se puede demostrar que los operadores LRL cuánticos satisfacen relaciones de conmutación exactamente análogas a las relaciones de corchete de Poisson en la sección anterior, simplemente reemplazando el corchete de Poisson por el conmutador. ^{[48] [49]} $${\displaystyle A_{s}=-mk{\hat {r}}_{s}+{\frac {1}{2}}\sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{sij}(p_{i}\ell _{j}+\ell _{j}p_{i}),}$$ ${\displaystyle 1/(i\hbar )}$

A partir de estos operadores, se pueden definir operadores de escalera adicionales para L. Estos conectan además diferentes estados propios de L ² , es decir, diferentes multipletes de espín, entre sí. $${\displaystyle {\begin{aligned}J_{0}&=A_{3},\\J_{\pm 1}&=\mp {\tfrac {1}{\sqrt {2}}}\left(A_{1}\pm iA_{2}\right).\end{aligned}}}$$

También se puede definir un primer operador invariante de Casimir normalizado, análogo cuántico del anterior, donde H ⁻¹ es el inverso del operador de energía hamiltoniano , e I es el operador identidad . $${\displaystyle C_{1}=-{\frac {mk^{2}}{2\hbar ^{2}}}H^{-1}-I,}$$

Aplicando estos operadores de escalera a los estados propios | ℓ mn〉 de los operadores de momento angular total, momento angular azimutal y energía, se ve que los valores propios del primer operador de Casimir, C ₁ , están cuantizados, n ² − 1 . Es importante destacar que, en virtud de la desaparición de C ₂ , son independientes de los números cuánticos ℓ y m , lo que hace que los niveles de energía se degeneren . ^[8]

Por lo tanto, los niveles de energía se dan por lo que coincide con la fórmula de Rydberg para átomos similares al hidrógeno (Figura 6). Los operadores de simetría adicionales A han conectado los diferentes multipletes ℓ entre sí, para una energía dada (y C ₁ ), dictando n ² estados en cada nivel. En efecto, han ampliado el grupo de momento angular SO(3) a SO(4) / Z ₂ ~ SO(3) × SO(3) . ^[50] $${\displaystyle E_{n}=-{\frac {mk^{2}}{2\hbar ^{2}n^{2}}},}$$

Conservación y simetría

La conservación del vector LRL corresponde a una simetría sutil del sistema. En mecánica clásica , las simetrías son operaciones continuas que mapean una órbita sobre otra sin cambiar la energía del sistema; en mecánica cuántica, las simetrías son operaciones continuas que "mezclan" orbitales electrónicos de la misma energía, es decir, niveles de energía degenerados. Una cantidad conservada suele estar asociada con tales simetrías. ^[1] Por ejemplo, cada fuerza central es simétrica bajo el grupo de rotación SO(3) , lo que conduce a la conservación del momento angular L . Clásicamente, una rotación general del sistema no afecta la energía de una órbita; en mecánica cuántica, las rotaciones mezclan los armónicos esféricos del mismo número cuántico ℓ sin cambiar la energía.

Figura 7: Familia de hodógrafas de momento circular para una energía dada E . Todos los círculos pasan por los mismos dos puntos en el eje p _x (ver Figura 3). Esta familia de hodógrafas corresponde a una familia de círculos apolíneos y a las isosuperficies σ de coordenadas bipolares . ${\textstyle \pm p_{0}=\pm {\sqrt {2m|E|}}}$

La simetría de la fuerza central inversa del cuadrado es mayor y más sutil. La simetría peculiar del problema de Kepler da como resultado la conservación tanto del vector de momento angular L como del vector LRL A ​​(tal como se definió anteriormente) y, desde el punto de vista de la mecánica cuántica, garantiza que los niveles de energía del hidrógeno no dependan de los números cuánticos de momento angular ℓ y m . Sin embargo, la simetría es más sutil porque la operación de simetría debe tener lugar en un espacio de dimensiones superiores ; a estas simetrías a menudo se las llama "simetrías ocultas". ^[51]

Clásicamente, la mayor simetría del problema de Kepler permite alteraciones continuas de las órbitas que preservan la energía pero no el momento angular; expresado de otra manera, las órbitas de la misma energía pero diferente momento angular (excentricidad) pueden transformarse continuamente unas en otras. En mecánica cuántica, esto corresponde a la mezcla de orbitales que difieren en los números cuánticos ℓ y m , como los orbitales atómicos s ( ℓ = 0 ) y p ( ℓ = 1 ). Tal mezcla no se puede hacer con traslaciones o rotaciones tridimensionales ordinarias, sino que es equivalente a una rotación en una dimensión superior.

Para energías negativas , es decir, para sistemas ligados, el grupo de simetría superior es SO(4) , que preserva la longitud de los vectores de cuatro dimensiones.

$${\displaystyle |\mathbf {e} |^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}+e_{4}^{2}.}$$

En 1935, Vladimir Fock demostró que el problema de Kepler limitado en mecánica cuántica es equivalente al problema de una partícula libre confinada en una esfera unitaria tridimensional en un espacio de cuatro dimensiones. ^[10] Específicamente, Fock demostró que la función de onda de Schrödinger en el espacio de momento para el problema de Kepler era la proyección estereográfica de los armónicos esféricos en la esfera. La rotación de la esfera y la reproyección dan como resultado un mapeo continuo de las órbitas elípticas sin cambiar la energía, una simetría SO(4) a veces conocida como simetría de Fock ; ^[52] mecánica cuántica, esto corresponde a una mezcla de todos los orbitales del mismo número cuántico de energía n . Valentine Bargmann señaló posteriormente que los corchetes de Poisson para el vector de momento angular L y el vector LRL escalado A formaban el álgebra de Lie para SO(4) . ^{[11] [42]} En términos simples, las seis cantidades A y L corresponden a los seis momentos angulares conservados en cuatro dimensiones, asociados con las seis posibles rotaciones simples en ese espacio (hay seis maneras de elegir dos ejes de entre cuatro). Esta conclusión no implica que nuestro universo sea una esfera tridimensional; simplemente significa que este problema de física particular (el problema de los dos cuerpos para las fuerzas centrales de la inversa del cuadrado) es matemáticamente equivalente a una partícula libre en una esfera tridimensional.

Para energías positivas , es decir, para sistemas no ligados, "dispersos", el grupo de simetría superior es SO(3,1) , que preserva la longitud de Minkowski de los 4 vectores.

$${\displaystyle ds^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}-e_{4}^{2}.}$$

^{Fock [10]} y Bargmann ^[11] consideraron los casos de energía negativa y positiva y Bander e Itzykson los revisaron enciclopédicamente. ^{[53] [54]}

Las órbitas de los sistemas de fuerza central –y las del problema de Kepler en particular– también son simétricas bajo reflexión . Por lo tanto, los grupos SO(3) , SO(4) y SO(3,1) citados anteriormente no son los grupos de simetría completa de sus órbitas; los grupos completos son O(3) , O(4) y O(3,1) , respectivamente. Sin embargo, solo los subgrupos conexos , SO(3) , SO(4) y SO ⁺ (3,1) , son necesarios para demostrar la conservación del momento angular y los vectores LRL; la simetría de reflexión es irrelevante para la conservación, que puede derivarse del álgebra de Lie del grupo.

Simetría rotacional en cuatro dimensiones

Figura 8: Las hodógrafas de momento de la Figura 7 corresponden a proyecciones estereográficas de círculos máximos sobre la esfera unitaria tridimensional η . Todos los círculos máximos intersecan el eje η _x , que es perpendicular a la página; la proyección es desde el polo norte (el vector unitario w ) hasta el plano η _x − η _y , como se muestra aquí para la hodógrafa magenta mediante las líneas discontinuas negras. El círculo máximo en una latitud α corresponde a una excentricidad e = sen α . Los colores de los círculos máximos que se muestran aquí corresponden a sus correspondientes hodógrafas en la Figura 7.

La conexión entre el problema de Kepler y la simetría rotacional de cuatro dimensiones SO(4) se puede visualizar fácilmente. ^{[53] [55] [56]} Sean las coordenadas cartesianas de cuatro dimensiones ( w , x , y , z ) donde ( x , y , z ) representan las coordenadas cartesianas del vector de posición normal r . El vector de momento tridimensional p está asociado con un vector de cuatro dimensiones en una esfera unitaria tridimensional ${\displaystyle {\boldsymbol {\eta }}}$

$${\displaystyle {\begin{aligned}{\boldsymbol {\eta }}&={\frac {p^{2}-p_{0}^{2}}{p^{2}+p_{0}^{2}}}\mathbf {\hat {w}} +{\frac {2p_{0}}{p^{2}+p_{0}^{2}}}\mathbf {p} \\[1em]&={\frac {mk-rp_{0}^{2}}{mk}}\mathbf {\hat {w}} +{\frac {rp_{0}}{mk}}\mathbf {p} ,\end{aligned}}}$$

donde es el vector unitario a lo largo del nuevo eje w . La transformación que mapea p a η se puede invertir de manera única; por ejemplo, el componente x del momento es igual a y de manera similar para p _y y p _z . En otras palabras, el vector tridimensional p es una proyección estereográfica del vector tetradimensional , escalado por p ₀ (Figura 8). ${\displaystyle \mathbf {\hat {w}} }$ $${\displaystyle p_{x}=p_{0}{\frac {\eta _{x}}{1-\eta _{w}}},}$$ ${\displaystyle {\boldsymbol {\eta }}}$

Sin pérdida de generalidad, podemos eliminar la simetría rotacional normal eligiendo las coordenadas cartesianas de modo que el eje z esté alineado con el vector de momento angular L y las hodógrafas de momento estén alineadas como en la Figura 7, con los centros de los círculos en el eje y . Puesto que el movimiento es plano, y p y L son perpendiculares, p _z = η _z = 0 y la atención puede restringirse al vector tridimensional . La familia de círculos apolíneos de hodógrafas de momento (Figura 7) corresponde a una familia de círculos máximos en la esfera tridimensional , todos los cuales intersecan el eje η _x en los dos focos η _x = ±1 , correspondientes a los focos de la hodógrafa de momento en p _x = ± p ₀ . Estos círculos máximos están relacionados por una rotación simple sobre el eje η _x (Figura 8). Esta simetría rotacional transforma todas las órbitas de la misma energía entre sí; Sin embargo, dicha rotación es ortogonal a las rotaciones tridimensionales habituales, ya que transforma la cuarta dimensión η _w . Esta mayor simetría es característica del problema de Kepler y corresponde a la conservación del vector LRL. ${\displaystyle {\boldsymbol {\eta }}=(\eta _{w},\eta _{x},\eta _{y})}$ ${\displaystyle {\boldsymbol {\eta }}}$

Se puede obtener una solución elegante de variables de ángulo de acción para el problema de Kepler eliminando las coordenadas tetradimensionales redundantes en favor de coordenadas cilíndricas elípticas ( χ , ψ , φ ) ^[57] ${\displaystyle {\boldsymbol {\eta }}}$

$${\displaystyle {\begin{aligned}\eta _{w}&=\operatorname {cn} \chi \operatorname {cn} \psi ,\\[1ex]\eta _{x}&=\operatorname {sn} \chi \operatorname {dn} \psi \cos \phi ,\\[1ex]\eta _{y}&=\operatorname {sn} \chi \operatorname {dn} \psi \sin \phi ,\\[1ex]\eta _{z}&=\operatorname {dn} \chi \operatorname {sn} \psi ,\end{aligned}}}$$donde sn , cn y dn son las funciones elípticas de Jacobi .

Generalizaciones a otros potenciales y relatividad

El vector de Laplace-Runge-Lenz también se puede generalizar para identificar cantidades conservadas que se aplican a otras situaciones.

En presencia de un campo eléctrico uniforme E , el vector Laplace-Runge-Lenz generalizado es ^{[17] [58]} ${\displaystyle {\mathcal {A}}}$

$${\displaystyle {\mathcal {A}}=\mathbf {A} +{\frac {mq}{2}}\left[\left(\mathbf {r} \times \mathbf {E} \right)\times \mathbf {r} \right],}$$donde q es la carga de la partícula en órbita. Aunque no se conserva, da lugar a una cantidad conservada, a saber . ${\displaystyle {\mathcal {A}}}$ ${\displaystyle {\mathcal {A}}\cdot \mathbf {E} }$

Generalizando aún más el vector de Laplace-Runge-Lenz a otros potenciales y a la relatividad especial , la forma más general se puede escribir como ^[18] $${\displaystyle {\mathcal {A}}=\left({\frac {\partial \xi }{\partial u}}\right)\left(\mathbf {p} \times \mathbf {L} \right)+\left[\xi -u\left({\frac {\partial \xi }{\partial u}}\right)\right]L^{2}\mathbf {\hat {r}} ,}$$

donde u = 1/ r y ξ = cos θ , con el ángulo θ definido por

$${\displaystyle \theta =L\int ^{u}{\frac {du}{\sqrt {m^{2}c^{2}(\gamma ^{2}-1)-L^{2}u^{2}}}},}$$

y γ es el factor de Lorentz . Como antes, podemos obtener un vector binormal conservado B tomando el producto vectorial con el vector de momento angular conservado

$${\displaystyle {\mathcal {B}}=\mathbf {L} \times {\mathcal {A}}.}$$

Estos dos vectores también pueden combinarse en un tensor diádico conservado W ,

$${\displaystyle {\mathcal {W}}=\alpha {\mathcal {A}}\otimes {\mathcal {A}}+\beta \,{\mathcal {B}}\otimes {\mathcal {B}}.}$$

En la ilustración, se puede calcular el vector LRL para un oscilador armónico isótropo no relativista. ^[18] Dado que la fuerza es central, el vector del momento angular se conserva y el movimiento se encuentra en un plano. $${\displaystyle \mathbf {F} (r)=-k\mathbf {r} ,}$$

El tensor diádico conservado se puede escribir en una forma simple aunque p y r no sean necesariamente perpendiculares. $${\displaystyle {\mathcal {W}}={\frac {1}{2m}}\mathbf {p} \otimes \mathbf {p} +{\frac {k}{2}}\,\mathbf {r} \otimes \mathbf {r} ,}$$

El vector Runge-Lenz correspondiente es más complicado, donde es la frecuencia de oscilación natural y $${\displaystyle {\mathcal {A}}={\frac {1}{\sqrt {mr^{2}\omega _{0}A-mr^{2}E+L^{2}}}}\left\{\left(\mathbf {p} \times \mathbf {L} \right)+\left(mr\omega _{0}A-mrE\right)\mathbf {\hat {r}} \right\},}$$ $${\displaystyle \omega _{0}={\sqrt {\frac {k}{m}}}}$$ $${\displaystyle A=(E^{2}-\omega ^{2}L^{2})^{1/2}/\omega .}$$

Pruebas de que el vector de Laplace-Runge-Lenz se conserva en los problemas de Kepler

Los siguientes son argumentos que muestran que el vector LRL se conserva bajo fuerzas centrales que obedecen una ley del cuadrado inverso.

Prueba directa de conservación

Una fuerza central que actúa sobre la partícula es ${\displaystyle \mathbf {F} }$

$${\displaystyle \mathbf {F} ={\frac {d\mathbf {p} }{dt}}=f(r){\frac {\mathbf {r} }{r}}=f(r)\mathbf {\hat {r}} }$$

para alguna función del radio . Dado que el momento angular se conserva bajo fuerzas centrales, y ${\displaystyle f(r)}$ ${\displaystyle r}$ ${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }$ ${\textstyle {\frac {d}{dt}}\mathbf {L} =0}$

$${\displaystyle {\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)={\frac {d\mathbf {p} }{dt}}\times \mathbf {L} =f(r)\mathbf {\hat {r}} \times \left(\mathbf {r} \times m{\frac {d\mathbf {r} }{dt}}\right)=f(r){\frac {m}{r}}\left[\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}\right],}$$

donde el momento y el producto triple cruz se han simplificado utilizando la fórmula de Lagrange ${\textstyle \mathbf {p} =m{\frac {d\mathbf {r} }{dt}}}$

$${\displaystyle \mathbf {r} \times \left(\mathbf {r} \times {\frac {d\mathbf {r} }{dt}}\right)=\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}.}$$

La identidad

$${\displaystyle {\frac {d}{dt}}\left(\mathbf {r} \cdot \mathbf {r} \right)=2\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}={\frac {d}{dt}}(r^{2})=2r{\frac {dr}{dt}}}$$

produce la ecuación

$${\displaystyle {\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=-mf(r)r^{2}\left[{\frac {1}{r}}{\frac {d\mathbf {r} }{dt}}-{\frac {\mathbf {r} }{r^{2}}}{\frac {dr}{dt}}\right]=-mf(r)r^{2}{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right).}$$

Para el caso especial de una fuerza central inversamente cuadrada , esto es igual a ${\textstyle f(r)={\frac {-k}{r^{2}}}}$

$${\displaystyle {\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=mk{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right)={\frac {d}{dt}}(mk\mathbf {\hat {r}} ).}$$

Por lo tanto, A se conserva para fuerzas centrales de cuadrado inverso ^[59]

$${\displaystyle {\frac {d}{dt}}\mathbf {A} ={\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)-{\frac {d}{dt}}\left(mk\mathbf {\hat {r}} \right)=\mathbf {0} .}$$

Una prueba más breve se obtiene utilizando la relación entre el momento angular y la velocidad angular, , que se cumple para una partícula que se desplaza en un plano perpendicular a . Especificando las fuerzas centrales de inverso cuadrado, la derivada temporal de es donde se cumple la última igualdad porque un vector unitario solo puede cambiar por rotación, y es la velocidad orbital del vector giratorio. Por lo tanto, se ve que A es una diferencia de dos vectores con derivadas temporales iguales. ${\displaystyle \mathbf {L} =mr^{2}{\boldsymbol {\omega }}}$ ${\displaystyle \mathbf {L} }$ ${\displaystyle \mathbf {p} \times \mathbf {L} }$ $${\displaystyle {\frac {d}{dt}}\mathbf {p} \times \mathbf {L} =\left({\frac {-k}{r^{2}}}\mathbf {\hat {r}} \right)\times \left(mr^{2}{\boldsymbol {\omega }}\right)=mk\,{\boldsymbol {\omega }}\times \mathbf {\hat {r}} =mk\,{\frac {d}{dt}}\mathbf {\hat {r}} ,}$$ ${\displaystyle {\boldsymbol {\omega }}\times \mathbf {\hat {r}} }$

Como se describe en otra parte de este artículo, este vector LRL A ​​es un caso especial de un vector conservado general que se puede definir para todas las fuerzas centrales. ^{[18] [19]} Sin embargo, dado que la mayoría de las fuerzas centrales no producen órbitas cerradas (véase el teorema de Bertrand ), el vector análogo rara vez tiene una definición simple y generalmente es una función multivalor del ángulo θ entre r y . ${\displaystyle {\mathcal {A}}}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle {\mathcal {A}}}$

Ecuación de Hamilton-Jacobi en coordenadas parabólicas

La constancia del vector LRL también se puede derivar de la ecuación de Hamilton-Jacobi en coordenadas parabólicas ( ξ , η ) , que se definen por las ecuaciones donde r representa el radio en el plano de la órbita $${\displaystyle {\begin{aligned}\xi &=r+x,\\\eta &=r-x,\end{aligned}}}$$ $${\displaystyle r={\sqrt {x^{2}+y^{2}}}.}$$

La inversión de estas coordenadas es $${\displaystyle {\begin{aligned}x&={\tfrac {1}{2}}(\xi -\eta ),\\y&={\sqrt {\xi \eta }},\end{aligned}}}$$

La separación de la ecuación de Hamilton-Jacobi en estas coordenadas produce las dos ecuaciones equivalentes ^{[17] [60]}

$${\displaystyle {\begin{aligned}2\xi p_{\xi }^{2}-mk-mE\xi &=-\Gamma ,\\2\eta p_{\eta }^{2}-mk-mE\eta &=\Gamma ,\end{aligned}}}$$donde Γ es una constante de movimiento. La resta y la reexpresión en términos de los momentos cartesianos p _x y p _y muestra que Γ es equivalente al vector LRL

$${\displaystyle \Gamma =p_{y}(xp_{y}-yp_{x})-mk{\frac {x}{r}}=A_{x}.}$$

Teorema de Noether

La conexión entre la simetría rotacional descrita anteriormente y la conservación del vector LRL se puede cuantificar mediante el teorema de Noether . Este teorema, que se utiliza para hallar constantes de movimiento, establece que cualquier variación infinitesimal de las coordenadas generalizadas de un sistema físico

$${\displaystyle \delta q_{i}=\varepsilon g_{i}(\mathbf {q} ,\mathbf {\dot {q}} ,t)}$$

que hace que el Lagrangiano varíe hasta el primer orden por una derivada de tiempo total

$${\displaystyle \delta L=\varepsilon {\frac {d}{dt}}G(\mathbf {q} ,t)}$$

corresponde a una cantidad conservada Γ

$${\displaystyle \Gamma =-G+\sum _{i}g_{i}\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\right).}$$

En particular, el componente vectorial LRL conservado A _s corresponde a la variación en las coordenadas ^[61]

$${\displaystyle \delta _{s}x_{i}={\frac {\varepsilon }{2}}\left[2p_{i}x_{s}-x_{i}p_{s}-\delta _{is}\left(\mathbf {r} \cdot \mathbf {p} \right)\right],}$$

donde i es igual a 1, 2 y 3, siendo x _i y p _i los componentes i -ésimos de los vectores de posición y momento r y p , respectivamente; como es habitual, δ representa el delta de Kronecker . El cambio de primer orden resultante en el lagrangiano _es

$${\displaystyle \delta L={\frac {1}{2}}\varepsilon mk{\frac {d}{dt}}\left({\frac {x_{s}}{r}}\right).}$$

La sustitución en la fórmula general para la cantidad conservada Γ produce el componente conservado A _s del vector LRL, $${\displaystyle A_{s}=\left[p^{2}x_{s}-p_{s}\ \left(\mathbf {r} \cdot \mathbf {p} \right)\right]-mk\left({\frac {x_{s}}{r}}\right)=\left[\mathbf {p} \times \left(\mathbf {r} \times \mathbf {p} \right)\right]_{s}-mk\left({\frac {x_{s}}{r}}\right).}$$

Transformación de mentiras

Figura 9: La transformación de Lie de la que se deriva la conservación del vector LRL A. A medida que varía el parámetro de escala λ , la energía y el momento angular cambian, pero no así la excentricidad e y la magnitud y dirección de A.

La derivación del teorema de Noether de la conservación del vector LRL A ​​es elegante, pero tiene un inconveniente: la variación de coordenadas δx _i involucra no solo la posición r , sino también el momento p o, equivalentemente, la velocidad v . ^[62] Este inconveniente se puede eliminar derivando en su lugar la conservación de A utilizando un enfoque iniciado por Sophus Lie . ^{[63] [64]} Específicamente, se puede definir una transformación de Lie ^[51] en la que las coordenadas r y el tiempo t se escalan por diferentes potencias de un parámetro λ (Figura 9), $${\displaystyle t\rightarrow \lambda ^{3}t,\qquad \mathbf {r} \rightarrow \lambda ^{2}\mathbf {r} ,\qquad \mathbf {p} \rightarrow {\frac {1}{\lambda }}\mathbf {p} .}$$

Esta transformación cambia el momento angular total L y la energía E , pero conserva su producto EL ² . Por lo tanto, la excentricidad e y la magnitud A se conservan, como se puede ver en la ecuación para A2 $${\displaystyle L\rightarrow \lambda L,\qquad E\rightarrow {\frac {1}{\lambda ^{2}}}E,}$$ $${\displaystyle A^{2}=m^{2}k^{2}e^{2}=m^{2}k^{2}+2mEL^{2}.}$$

La dirección de A también se conserva, ya que los semiejes no se modifican mediante una escala global. Esta transformación también conserva la tercera ley de Kepler , es decir, que el semieje a y el período T forman una constante  T ² / a ³ .

Escalas, símbolos y formulaciones alternativas

A diferencia de los vectores de momento y momento angular p y L , no existe una definición universalmente aceptada del vector de Laplace-Runge-Lenz; en la literatura científica se utilizan varios factores de escala y símbolos diferentes. La definición más común se da arriba, pero otra alternativa común es dividir por la cantidad mk para obtener un vector de excentricidad conservada adimensional

$${\displaystyle \mathbf {e} ={\frac {1}{mk}}\left(\mathbf {p} \times \mathbf {L} \right)-\mathbf {\hat {r}} ={\frac {m}{k}}\left(\mathbf {v} \times \left(\mathbf {r} \times \mathbf {v} \right)\right)-\mathbf {\hat {r}} ,}$$

donde v es el vector de velocidad. Este vector escalado e tiene la misma dirección que A y su magnitud es igual a la excentricidad de la órbita, por lo que se anula en órbitas circulares.

También son posibles otras versiones escaladas, por ejemplo, dividiendo A por m solamente o por p ₀ que tiene las mismas unidades que el vector de momento angular L . $${\displaystyle \mathbf {M} =\mathbf {v} \times \mathbf {L} -k\mathbf {\hat {r}} ,}$$ $${\displaystyle \mathbf {D} ={\frac {\mathbf {A} }{p_{0}}}={\frac {1}{\sqrt {2m|E|}}}\left\{\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}} \right\},}$$

En casos excepcionales, el signo del vector LRL puede invertirse, es decir, escalarse en −1 . Otros símbolos comunes para el vector LRL incluyen a , R , F , J y V. Sin embargo, la elección de la escala y el símbolo para el vector LRL no afectan su conservación.

Figura 4: El vector de momento angular L , el vector LRL A ​​y el vector de Hamilton, el binormal B , son mutuamente perpendiculares; A y B apuntan a lo largo de los ejes mayor y menor, respectivamente, de una órbita elíptica del problema de Kepler.

Un vector conservado alternativo es el vector binormal B estudiado por William Rowan Hamilton, ^[16]

${\displaystyle \mathbf {B} =\mathbf {p} -\left({\frac {mk}{L^{2}r}}\right)\ \left(\mathbf {L} \times \mathbf {r} \right),}$

que se conserva y apunta a lo largo del semieje menor de la elipse. (No está definido para excentricidad evanescente).

El vector LRL A ​​= B × L es el producto vectorial de B y L (Figura 4). En la hodógrafa de momento de la sección correspondiente anterior, se ve fácilmente que B conecta el origen de los momentos con el centro de la hodógrafa circular y que posee magnitud A / L . En el perihelio, apunta en la dirección del momento.

El vector B se denomina "binormal" ya que es perpendicular tanto a A como a L. De manera similar al propio vector LRL, el vector binormal se puede definir con diferentes escalas y símbolos.

Los dos vectores conservados, A y B, se pueden combinar para formar un tensor diádico conservado W , ^[18] donde α y β son constantes de escala arbitrarias y representan el producto tensorial (que no está relacionado con el producto vectorial , a pesar de su símbolo similar). Escrita en componentes explícitos, esta ecuación se lee $${\displaystyle \mathbf {W} =\alpha \mathbf {A} \otimes \mathbf {A} +\beta \,\mathbf {B} \otimes \mathbf {B} ,}$$ ${\displaystyle \otimes }$ $${\displaystyle W_{ij}=\alpha A_{i}A_{j}+\beta B_{i}B_{j}.}$$

Al ser perpendiculares entre sí, los vectores A y B pueden considerarse como los ejes principales del tensor conservado W , es decir, sus vectores propios escalados . W es perpendicular a L , ya que A y B también son perpendiculares a L , L ⋅ A = L ⋅ B = 0 . $${\displaystyle \mathbf {L} \cdot \mathbf {W} =\alpha \left(\mathbf {L} \cdot \mathbf {A} \right)\mathbf {A} +\beta \left(\mathbf {L} \cdot \mathbf {B} \right)\mathbf {B} =0,}$$

Más directamente, esta ecuación se lee, en componentes explícitos, $${\displaystyle \left(\mathbf {L} \cdot \mathbf {W} \right)_{j}=\alpha \left(\sum _{i=1}^{3}L_{i}A_{i}\right)A_{j}+\beta \left(\sum _{i=1}^{3}L_{i}B_{i}\right)B_{j}=0.}$$

Véase también

• Astrodinámica
  • Órbita
  • Vector de excentricidad
  • Elementos orbitales
• Teorema de Bertrand
• Ecuación de Binet
• Problema de dos cuerpos

Referencias

1. Goldstein, H. (1980). Mecánica clásica (2.ª ed.). Addison Wesley. págs. 102–105, 421–422.
2. Taff, LG (1985). Mecánica celeste: una guía computacional para el profesional . Nueva York: John Wiley and Sons. págs. 42–43.
3. Goldstein, H. (1980). Mecánica clásica (2.ª ed.). Addison Wesley. págs. 94–102.
4. Arnold, VI (1989). Métodos matemáticos de la mecánica clásica (2.ª ed.). Nueva York: Springer-Verlag. pág. 38. ISBN 0-387-96890-3.
5. Sommerfeld, A. (1964). Mecánica . Lecciones de física teórica. Vol. 1. Traducido por Martin O. Stern (4.ª ed.). Nueva York: Academic Press. pp. 38–45.
6. Lanczos, C. (1970). Los principios variacionales de la mecánica (4ª ed.). Nueva York: Dover Publications. págs. 118, 129, 242, 248.
7. Pauli, W. (1926). "Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik". Zeitschrift für Physik . 36 (5): 336–363. Código bibliográfico : 1926ZPhy...36..336P. doi :10.1007/BF01450175. S2CID  128132824.
8. Bohm, A. (1993). Mecánica cuántica: fundamentos y aplicaciones (3.ª ed.). Nueva York: Springer-Verlag. págs. 205–222.
9. Hanca, J.; Tulejab, S.; Hancova, M. (2004). "Simetrías y leyes de conservación: consecuencias del teorema de Noether". American Journal of Physics . 72 (4): 428–35. Bibcode :2004AmJPh..72..428H. doi :10.1119/1.1591764.
10. Fock, V. (1935). "Zur Theorie des Wasserstoffatoms". Zeitschrift für Physik . 98 (3–4): 145–154. Código bibliográfico : 1935ZPhy...98..145F. doi :10.1007/BF01336904. S2CID  123112334.
11. abcdeBargmann, V. (1936). "Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock". Zeitschrift für Physik . 99 (7–8): 576–582. Código bibliográfico : 1936ZPhy...99..576B. doi :10.1007/BF01338811. S2CID  117461194.
12. Hamilton, WR (1847). "La hodógrafa o un nuevo método de expresión en lenguaje simbólico de la ley de atracción de Newton". Actas de la Real Academia Irlandesa . 3 : 344–353.
13. Goldstein, H. (1980). Mecánica clásica (2.ª ed.). Addison Wesley. pág. 421.
14. Arnold, VI (1989). Métodos matemáticos de la mecánica clásica (2.ª ed.). Nueva York: Springer-Verlag. pp. 413–415. ISBN 0-387-96890-3.
15. Goldstein, H. (1975). "Prehistoria del vector de Runge-Lenz". American Journal of Physics . 43 (8): 737–738. Código Bibliográfico :1975AmJPh..43..737G. doi :10.1119/1.9745.
    Goldstein, H. (1976). "Más sobre la prehistoria del vector Runge–Lenz". American Journal of Physics . 44 (11): 1123–1124. Código Bibliográfico :1976AmJPh..44.1123G. doi :10.1119/1.10202.
16. Hamilton, WR (1847). "Aplicaciones de los cuaterniones a algunas cuestiones dinámicas". Actas de la Real Academia Irlandesa . 3 : Apéndice III.
17. Landau, LD ; Lifshitz EM (1976). Mecánica (3.ª ed.). Pergamon Press. pág. 154. ISBN 0-08-021022-8.
18. Fradkin, DM (1967). "Existencia de las simetrías dinámicas O4 y SU3 para todos los problemas de potencial central clásicos". Progreso de la física teórica . 37 (5): 798–812. Bibcode :1967PThPh..37..798F. doi : 10.1143/PTP.37.798 .
19. Yoshida, T. (1987). "Dos métodos de generalización del vector de Laplace–Runge–Lenz". Revista Europea de Física . 8 (4): 258–259. Código Bibliográfico :1987EJPh....8..258Y. doi :10.1088/0143-0807/8/4/005. S2CID  250843588.
20. Goldstein, H. (1980). Mecánica clásica (2.ª ed.). Addison Wesley. págs. 1–11.
21. Symon, KR (1971). Mecánica (3.ª ed.). Addison Wesley. págs. 103–109, 115–128.
22. Hermann, J. (1710). "Metodo d'investigare l'Orbite de' Pianeti, nell' ipotesi che le forze centrali o pure le gravità degli stessi Pianeti sono in ragione reciproca de' quadrati delle distanze, che i medesimi tengono dal Centro, a cui si dirigono le forze stesse ". Giornale de Letterati d'Italia . 2 : 447–467.
    Hermann, J. (1710). "Extrait d'une lettre de M. Herman à M. Bernoulli fechada de Padoüe le 12. Juillet 1710". Historia de la Academia Real de Ciencias . 1732 : 519–521.
23. Bernoulli, J. (1710). "Extrait de la Réponse de M. Bernoulli à M. Herman fechada en Basilea el 7 de octubre de 1710". Historia de la Academia Real de Ciencias . 1732 : 521–544.
24. Laplace, PS (1799). Traité de mecanique celeste. París, Duprat. Tomo I, Premiere Partie, Livre II, págs.165 y siguientes.
25. Gibbs, JW ; Wilson EB (1901). Análisis vectorial. Nueva York: Scribners. pág. 135.
26. Runge, C. (1919). Análisis vectorial . vol. I. Leipzig: Hirzel.
27. Lenz, W. (1924). "Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung". Zeitschrift für Physik . 24 (1): 197–207. Código bibliográfico : 1924ZPhy...24..197L. doi :10.1007/BF01327245. S2CID  121552327.
28. Symon, KR (1971). Mecánica (3.ª ed.). Addison Wesley. págs. 130–131.
29. El vector binormal de Hamilton conservado en este plano de momento (rosa) tiene un significado geométrico más simple y, de hecho, puede reemplazarlo, como se ve en Patera, RP (1981). "Momentum-space derivation of the Runge-Lenz vector", Am. J. Phys 49 593–594. Tiene una longitud A / L y se analiza en la sección #Escalamientos alternativos, símbolos y formulaciones. ${\displaystyle \mathbf {B} \equiv \mathbf {L} \times \mathbf {A} /L^{2}}$ ${\displaystyle \mathbf {A} =\mathbf {B} \times \mathbf {L} }$
30. Evans, NW (1990). "Superintegrabilidad en mecánica clásica". Physical Review A . 41 (10): 5666–5676. Bibcode :1990PhRvA..41.5666E. doi :10.1103/PhysRevA.41.5666. PMID  9902953.
31. Sommerfeld, A. (1923). Estructura atómica y líneas espectrales . Londres: Methuen. pág. 118.
32. Curtright, T.; Zachos C. (2003). "Mecánica clásica y cuántica de Nambu". Physical Review . D68 (8): 085001. arXiv : hep-th/0212267 . Código Bibliográfico :2003PhRvD..68h5001C. doi :10.1103/PhysRevD.68.085001. S2CID  17388447.
33. Evans, NW (1991). "Teoría de grupos del sistema Smorodinsky–Winternitz". Revista de Física Matemática . 32 (12): 3369–3375. Bibcode :1991JMP....32.3369E. doi :10.1063/1.529449.
34. Zachos, C.; Curtright T. (2004). "Branas, corchetes cuánticos de Nambu y el átomo de hidrógeno". Revista Checa de Física . 54 (11): 1393–1398. arXiv : math-ph/0408012 . Código Bibliográfico :2004CzJPh..54.1393Z. doi :10.1007/s10582-004-9807-x. S2CID  14074249.
35. Einstein, A. (1915). "Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie". Sitzungsberichte der Preussischen Akademie der Wissenschaften . 1915 : 831–839. Código Bib : 1915SPAW.......831E.
36. Le Verrier, UJJ (1859). "Lettre de M. Le Verrier à M. Faye sur la Théorie de Mercure et sur le Mouvement du Périhélie de cette Planète". Cuentas Rendus de la Academia de Ciencias de París . 49 : 379–383.
37. Will, CM (1979). Relatividad general: un estudio de Einstein del siglo XX (ed. SW Hawking y W Israel). Cambridge: Cambridge University Press. Capítulo 2.
38. Pais, A. (1982). Sutil es el Señor: La ciencia y la vida de Albert Einstein . Oxford University Press.
39. Roseveare, NT (1982). El perihelio de Mercurio desde Le Verrier hasta Einstein . Oxford University Press. ISBN 978-0-19-858174-1.
40. Hall 2013 Proposición 17.25.
41. Hall 2013 Proposición 18.7; tenga en cuenta que Hall utiliza una normalización diferente del vector LRL.
42. Hall 2013 Teorema 18.9.
43. Hall 2013, Sección 18.4.4.
44. Efimov, SP (2022). "Modificación del espacio de coordenadas de la teoría de Fock. Tensores armónicos en el problema cuántico de Coulomb". Física-Uspekhi . 65 (9): 952–967. Bibcode :2022PhyU...65..952E. doi :10.3367/UFNe.2021.04.038966. S2CID  234871720.
45. Efimov, SP (2023). "Operador de Runge-Lenz en el espacio de momento". JETP Letters . 117 (9): 716–720. Código Bibliográfico :2023JETPL.117..716E. doi : 10.1134/S0021364023600635 . S2CID  259225778.
46. Dirac, PAM (1958). Principios de mecánica cuántica (4.ª edición revisada). Oxford University Press.
47. Schrödinger, E. (1926). "Quantisierung als Eigenwertproblem". Annalen der Physik . 384 (4): 361–376. Código bibliográfico : 1926AnP...384..361S. doi : 10.1002/andp.19263840404 .
48. Hall 2013 Proposición 18.12.
49. Merzbacher, Eugen (7 de enero de 1998). Mecánica cuántica. John Wiley & Sons. Págs. 268-270. ISBN. 978-0-471-88702-7.
50. Hall 2013 Teorema 18.14.
51. Prince, GE; Eliezer CJ (1981). "Sobre las simetrías de Lie del problema clásico de Kepler". Journal of Physics A: Mathematical and General . 14 (3): 587–596. Bibcode :1981JPhA...14..587P. doi :10.1088/0305-4470/14/3/009.
52. Nikitin, AG (7 de diciembre de 2012). "Nuevos sistemas exactamente resolubles con simetría de Fock". Journal of Physics A: Mathematical and Theoretical . 45 (48): 485204. arXiv : 1205.3094 . Bibcode :2012JPhA...45V5204N. doi :10.1088/1751-8113/45/48/485204. S2CID  119138270.
53. Bander, M.; Itzykson C. (1966). "Teoría de grupos y el átomo de hidrógeno (I)". Reseñas de física moderna . 38 (2): 330–345. Bibcode :1966RvMP...38..330B. doi :10.1103/RevModPhys.38.330.
54. Bander, M.; Itzykson C. (1966). "Teoría de grupos y el átomo de hidrógeno (II)". Reseñas de física moderna . 38 (2): 346–358. Código Bibliográfico :1966RvMP...38..346B. doi :10.1103/RevModPhys.38.346.
55. Rogers, HH (1973). "Transformaciones de simetría del problema clásico de Kepler". Journal of Mathematical Physics . 14 (8): 1125–1129. Bibcode :1973JMP....14.1125R. doi :10.1063/1.1666448.
56. Guillemin, V.; Sternberg S. (1990). Variaciones sobre un tema de Kepler . Vol. 42. Publicaciones del Colloquium de la American Mathematical Society. ISBN 0-8218-1042-1.
57. Lakshmanan, M.; Hasegawa H. (1984). "Sobre la equivalencia canónica del problema de Kepler en espacios de coordenadas y de momento". Journal of Physics A . 17 (16): L889–L893. Bibcode :1984JPhA...17L.889L. doi :10.1088/0305-4470/17/16/006.
58. Redmond, PJ (1964). "Generalización del vector de Runge-Lenz en presencia de un campo eléctrico". Physical Review . 133 (5B): B1352–B1353. Código Bibliográfico :1964PhRv..133.1352R. doi :10.1103/PhysRev.133.B1352.
59. Hall 2013 Proposición 2.34.
60. Dulock, VA; McIntosh HV (1966). "Sobre la degeneración del problema de Kepler". Revista del Pacífico de Matemáticas . 19 : 39–55. doi : 10.2140/pjm.1966.19.39 .
61. Lévy-Leblond, JM (1971). "Leyes de conservación para lagrangianos invariantes de calibre en mecánica clásica". American Journal of Physics . 39 (5): 502–506. Código Bibliográfico :1971AmJPh..39..502L. doi :10.1119/1.1986202.
62. Gonzalez-Gascon, F. (1977). "Notas sobre las simetrías de sistemas de ecuaciones diferenciales". Journal of Mathematical Physics . 18 (9): 1763–1767. Bibcode :1977JMP....18.1763G. doi :10.1063/1.523486.
63. Mentira, S. (1891). Vorlesungen über Differentialgleichungen. Leipzig: Teubner.
64. Ince, EL (1926). Ecuaciones diferenciales ordinarias . Nueva York: Dover (reimpresión de 1956). pp. 93–113.

Lectura adicional

• Baez, John (2008). "El problema de Kepler revisitado: el vector de Laplace-Runge-Lenz" (PDF) . Consultado el 31 de mayo de 2021 .
• Baez, John (2003). "Misterios del problema gravitacional de los dos cuerpos". Archivado desde el original el 21 de octubre de 2008. Consultado el 11 de diciembre de 2004 .
• Baez, John (2018). "Misterios del problema gravitacional de los dos cuerpos" . Consultado el 31 de mayo de 2021 .Versión actualizada de la fuente anterior.
• D'Eliseo, MM (2007). "La ecuación orbital de primer orden". American Journal of Physics . 75 (4): 352–355. Código Bibliográfico :2007AmJPh..75..352D. doi :10.1119/1.2432126.
• Hall, Brian C. (2013), Teoría cuántica para matemáticos , Textos de posgrado en matemáticas, vol. 267, Springer, Bibcode :2013qtm..book.....H, ISBN 978-1461471158.
• Leach, PGL; GP Flessas (2003). "Generalizaciones del vector de Laplace–Runge–Lenz". J. Nonlinear Math. Phys . 10 (3): 340–423. arXiv : math-ph/0403028 . Código Bibliográfico : 2003JNMP...10..340L. doi : 10.2991/jnmp.2003.10.3.6. S2CID  73707398.