

La ecuación del tiempo describe la discrepancia entre dos tipos de tiempo solar . La palabra ecuación se utiliza en el sentido medieval de "reconciliación de una diferencia". Los dos tiempos que difieren son el tiempo solar aparente , que sigue directamente el movimiento diurno del Sol , y el tiempo solar medio , que sigue un Sol medio teórico con movimiento uniforme a lo largo del ecuador celeste . El tiempo solar aparente se puede obtener midiendo la posición actual ( ángulo horario ) del Sol, como lo indica (con precisión limitada) un reloj de sol . La hora solar media , para un mismo lugar, sería la hora indicada por un reloj fijo ajustado de modo que a lo largo del año sus diferencias con la hora solar aparente tuvieran una media de cero. [1]
La ecuación del tiempo es el componente este u oeste del analema , una curva que representa el desplazamiento angular del Sol desde su posición media en la esfera celeste vista desde la Tierra. Las ecuaciones de valores de tiempo para cada día del año, compiladas por los observatorios astronómicos , aparecían ampliamente recogidas en almanaques y efemérides . [2] [3] : 14
La ecuación del tiempo se puede aproximar mediante la suma de dos ondas sinusoidales (ver explicación a continuación):
donde representa el número de días desde el 1 de enero del año en curso, .

Durante un año la ecuación del tiempo varía como se muestra en el gráfico; su cambio de un año a otro es leve. La hora aparente y el reloj de sol pueden adelantarse (rápido) hasta 16 min 33 s (alrededor del 3 de noviembre), o retrasarse (lento) hasta 14 min 6 s (alrededor del 11 de febrero). La ecuación del tiempo tiene ceros cerca del 15 de abril, 13 de junio, 1 de septiembre y 25 de diciembre. Haciendo caso omiso de cambios muy lentos en la órbita y la rotación de la Tierra, estos eventos se repiten en las mismas épocas cada año tropical . Sin embargo, debido al número no entero de días de un año, estas fechas pueden variar aproximadamente un día de un año a otro. [n 1] [4] : 277
La gráfica de la ecuación del tiempo se aproxima mucho mediante la suma de dos curvas sinusoidales, una con un período de un año y otra con un período de medio año. Las curvas reflejan dos efectos astronómicos, cada uno de los cuales provoca una falta de uniformidad diferente en el movimiento diario aparente del Sol en relación con las estrellas:
La ecuación del tiempo desaparece sólo para un planeta con inclinación axial cero y excentricidad orbital cero. [5] Dos ejemplos de planetas con grandes ecuaciones de tiempo son Marte y Urano. En Marte , la diferencia entre la hora del reloj de sol y la hora del reloj puede ser de hasta 50 minutos, debido a la excentricidad considerablemente mayor de su órbita. El planeta Urano , que tiene una inclinación axial extremadamente grande, tiene una ecuación del tiempo que hace que sus días comiencen y terminen varias horas antes o después dependiendo de dónde se encuentre en su órbita.
El Observatorio Naval de los Estados Unidos afirma que "la Ecuación del Tiempo es la diferencia del tiempo solar aparente menos el tiempo solar medio ", es decir, si el sol está adelantado al reloj el signo es positivo, y si el reloj está adelantado al sol el signo es negativo. . [6] [7] La ecuación del tiempo se muestra en el gráfico superior para un período de poco más de un año. El gráfico inferior (que cubre exactamente un año calendario) tiene los mismos valores absolutos pero el signo está invertido ya que muestra qué tan lejos está el reloj del sol. Las publicaciones pueden utilizar cualquiera de los formatos; en el mundo de habla inglesa, el primer uso es el más común, pero no siempre se sigue. Cualquiera que haga uso de una tabla o gráfico publicado debe comprobar primero su uso de signos. A menudo, hay una nota o un título que lo explica. De lo contrario, el uso se puede determinar sabiendo que, durante los primeros tres meses de cada año, el reloj está adelantado al reloj de sol. El mnemónico "NYSS" (pronunciado "nice"), para "año nuevo, reloj de sol lento", puede resultar útil. Algunas tablas publicadas evitan la ambigüedad al no utilizar signos, sino que muestran frases como "reloj de sol rápido" o "reloj de sol lento". [8]
En este artículo, y en otros de Wikipedia en inglés, un valor positivo de la ecuación del tiempo implica que un reloj de sol está adelantado a un reloj.
La frase "ecuación del tiempo" se deriva del latín medieval aequātiō diērum , que significa "ecuación de días" o "diferencia de días". La palabra aequātiō (y ecuación del inglés medio ) se usó en la astronomía medieval para tabular la diferencia entre un valor observado y el valor esperado (como en la ecuación del centro, la ecuación de los equinoccios, la ecuación del epiciclo). Gerald J. Toomer utiliza el término medieval "ecuación", del latín aequātiō , [n 2] para la diferencia de Ptolomeo entre el tiempo solar medio y el tiempo solar aparente. La definición de la ecuación de Johannes Kepler es "la diferencia entre el número de grados y minutos de la anomalía media y los grados y minutos de la anomalía corregida". [9] : 155
La diferencia entre el tiempo solar aparente y el tiempo medio fue reconocida por los astrónomos desde la antigüedad, pero antes de la invención de relojes mecánicos precisos a mediados del siglo XVII, los relojes de sol eran los únicos relojes fiables y el tiempo solar aparente era el estándar generalmente aceptado. El tiempo medio no sustituyó al tiempo aparente en los almanaques y efemérides nacionales hasta principios del siglo XIX. [10]
Los babilonios conocían el movimiento diario irregular del Sol. [ cita necesaria ]
El Libro III del Almagesto de Ptolomeo (siglo II) se ocupa principalmente de la anomalía del Sol, y tabuló la ecuación del tiempo en sus Handy Tables . [11] Ptolomeo analiza la corrección necesaria para convertir el cruce del meridiano del Sol en tiempo solar y toma en consideración el movimiento no uniforme del Sol a lo largo de la eclíptica y la corrección del meridiano para la longitud de la eclíptica del Sol. Afirma que la corrección máxima es 8.+1 ⁄ 3 grados de tiempo o 5 ⁄ 9 de hora (Libro III, capítulo 9). [12] Sin embargo, no consideró que el efecto fuera relevante para la mayoría de los cálculos, ya que era insignificante para las luminarias de movimiento lento y solo lo aplicó para la luminaria de movimiento más rápido, la Luna.
Basado en la discusión de Ptolomeo en el Almagesto , los valores para la ecuación del tiempo (árabe taʿdīl al-ayyām bi layālayhā ) eran estándar para las tablas ( zij ) en las obras de la astronomía islámica medieval . [13]
Nevil Maskelyne dio una descripción del tiempo aparente y medio en el Almanaque Náutico de 1767: "El tiempo aparente es el que se deduce inmediatamente del Sol, ya sea por la observación de su paso por el meridiano o por su salida o puesta observada . Esta vez es diferente del que muestran los Relojes y Vigilancias bien regulados en la Tierra, que se llama Tiempo igualado o medio." Continuó diciendo que, en el mar, el tiempo aparente obtenido a partir de la observación del Sol debe corregirse mediante la ecuación del tiempo, si el observador necesita el tiempo medio. [1]
Originalmente se consideraba que la hora adecuada era la que indicaba un reloj de sol. Cuando se introdujeron los buenos relojes mecánicos, coincidían con los relojes de sol sólo cerca de cuatro fechas cada año, por lo que se utilizó la ecuación del tiempo para "corregir" sus lecturas y obtener la hora del reloj de sol. Algunos relojes, llamados relojes de ecuaciones , incluían un mecanismo interno para realizar esta "corrección". Más tarde, cuando los relojes se convirtieron en los buenos relojes dominantes, el tiempo de reloj sin corregir, es decir, el "tiempo medio", se convirtió en el estándar aceptado. Las lecturas de los relojes de sol, cuando se utilizaban, eran entonces, y a menudo todavía lo son, corregidas con la ecuación del tiempo, utilizada en dirección inversa a la anterior, para obtener la hora del reloj. Muchos relojes de sol, por lo tanto, tienen grabadas tablas o gráficos de la ecuación del tiempo para permitir al usuario realizar esta corrección. [8] : 123
La ecuación del tiempo se utilizó históricamente para poner en hora los relojes. Entre la invención de los relojes precisos en 1656 y la llegada de los servicios comerciales de distribución del tiempo alrededor de 1900, hubo varias formas terrestres comunes de poner en hora los relojes. Un reloj de sol se leía y corregía con la tabla o gráfica de la ecuación del tiempo. Si se disponía de un instrumento de tránsito, se anotaba el tránsito del sol a través del meridiano (el momento en que el sol parece estar hacia el sur o el norte del observador); Luego se puso el reloj al mediodía y se compensó con el número de minutos dado por la ecuación del tiempo para esa fecha. Un tercer método no utilizó la ecuación del tiempo; en cambio, utilizó observaciones estelares para dar el tiempo sidéreo , explotando la relación entre el tiempo sidéreo y el tiempo solar medio . [14] : 57–58
Las primeras tablas que dan la ecuación del tiempo de forma esencialmente correcta fueron publicadas en 1665 por Christiaan Huygens . [15] Huygens, siguiendo la tradición de Ptolomeo y de los astrónomos medievales en general, estableció sus valores para la ecuación del tiempo de manera que todos los valores fueran positivos durante todo el año. [15] [n 3]
Otro conjunto de tablas fue publicado en 1672-73 por John Flamsteed , quien más tarde se convirtió en el primer Astrónomo Real del nuevo Observatorio Real de Greenwich . Éstas parecen haber sido las primeras tablas esencialmente correctas que dieron el significado actual de la hora media (anteriormente, como se señaló anteriormente, el signo de la ecuación siempre era positivo y se fijaba en cero cuando la hora aparente de salida del sol era más temprana en relación con el reloj). hora de salida del sol). Flamsteed adoptó la convención de tabular y nombrar la corrección en el sentido de que debía aplicarse al tiempo aparente para dar el tiempo medio. [dieciséis]
La ecuación del tiempo, basada correctamente en los dos componentes principales de la irregularidad del movimiento aparente del Sol, [n 4] no fue adoptada generalmente hasta después de las tablas de Flamsteed de 1672-73, publicadas con la edición póstuma de las obras de Jeremiah Horrocks . [17] : 49
Robert Hooke (1635-1703), que analizó matemáticamente la junta universal , fue el primero en notar que la geometría y la descripción matemática de la ecuación (no secular) del tiempo y la junta universal eran idénticas, y propuso el uso de una junta universal. conjunta en la construcción de un "reloj de sol mecánico". [18] : 219
Las correcciones en las tablas de Flamsteed de 1672-1673 y 1680 dieron el tiempo medio calculado esencialmente correctamente y sin necesidad de mayores compensaciones. Pero los valores numéricos en las tablas de la ecuación del tiempo han cambiado algo desde entonces debido a tres factores:

De 1767 a 1833, el Almanaque Náutico y las Efemérides Astronómicas británicos tabularon la ecuación del tiempo en el sentido de "sumar o restar (según las instrucciones) el número de minutos y segundos indicados hacia o desde el tiempo aparente para obtener el tiempo medio". Los tiempos en el Almanaque estaban en tiempo solar aparente, porque el tiempo a bordo de un barco se determinaba con mayor frecuencia mediante la observación del Sol. Esta operación se realizaría en el caso inusual de que se necesitara el tiempo solar medio de una observación. En las emisiones desde 1834, todos los tiempos se han indicado en tiempo solar medio, porque entonces el tiempo a bordo de los barcos se determinaba cada vez más mediante cronómetros marinos . En consecuencia, las instrucciones eran sumar o restar (según las instrucciones) el número de minutos indicados al tiempo medio o al tiempo medio para obtener el tiempo aparente. Entonces ahora la suma correspondía a que la ecuación fuera positiva y la resta correspondía a que fuera negativa.
Como el movimiento diario aparente del Sol es de una revolución por día, es decir, 360° cada 24 horas, y el Sol mismo aparece como un disco de aproximadamente 0,5° en el cielo, los relojes de sol simples se pueden leer con una precisión máxima de aproximadamente un minuto. Dado que la ecuación del tiempo tiene un rango de aproximadamente 33 minutos, no se puede ignorar la diferencia entre la hora del reloj de sol y la hora del reloj. Además de la ecuación del tiempo, también hay que aplicar correcciones debido a la distancia con respecto al meridiano de la zona horaria local y al horario de verano , si corresponde.
El pequeño aumento del día solar medio debido a la desaceleración de la rotación de la Tierra, de aproximadamente 2 ms por día por siglo, que actualmente se acumula hasta aproximadamente 1 segundo cada año, no se tiene en cuenta en las definiciones tradicionales de la ecuación de tiempo, ya que es imperceptible con el nivel de precisión de los relojes de sol.

La tierra gira alrededor del Sol. Visto desde la Tierra, el Sol parece girar una vez alrededor de la Tierra a través de las estrellas de fondo en un año. Si la Tierra orbitara alrededor del Sol con velocidad constante, en una órbita circular en un plano perpendicular al eje de la Tierra, entonces el Sol culminaría todos los días exactamente a la misma hora y sería un cronometrador perfecto (excepto por el efecto muy pequeño de la desaceleración de la rotación de la Tierra). Pero la órbita de la Tierra es una elipse no centrada en el Sol, y su velocidad varía entre 30,287 y 29,291 km/s, según las leyes del movimiento planetario de Kepler , y su velocidad angular también varía, por lo que el Sol parece moverse más rápido. (en relación con las estrellas de fondo) en el perihelio (actualmente alrededor del 3 de enero) y más lento en el afelio medio año después. [20] [21] [22]
En estos puntos extremos, este efecto varía el día solar aparente en 7,9 s/día con respecto a su media. En consecuencia, las diferencias diarias más pequeñas en otros días en velocidad son acumulativas hasta estos puntos, lo que refleja cómo el planeta acelera y desacelera en comparación con la media.
Como resultado, la excentricidad de la órbita de la Tierra contribuye con una variación periódica que es (en aproximación de primer orden) una onda sinusoidal con:
Este componente de la EoT está representado por el factor a antes mencionado :
a = -7.659 * Math.sin(6.24004077 + 0.01720197 * (365*(y-2000) + díadelaño))
Incluso si la órbita de la Tierra fuera circular, el movimiento percibido del Sol a lo largo de nuestro ecuador celeste aún no sería uniforme. [5] Esto es una consecuencia de la inclinación del eje de rotación de la Tierra con respecto al plano de su órbita , o equivalentemente, la inclinación de la eclíptica (el camino que parece tomar el Sol en la esfera celeste ) con respecto a la esfera celeste. ecuador . La proyección de este movimiento sobre nuestro ecuador celeste , a lo largo del cual se mide el "tiempo del reloj", es máxima en los solsticios , cuando el movimiento anual del Sol es paralelo al ecuador (lo que provoca una amplificación de la velocidad percibida) y produce principalmente un cambio. en recta ascensión . Es un mínimo en los equinoccios , cuando el movimiento aparente del Sol es más inclinado y produce más cambios en la declinación , dejando menos para la componente en ascensión recta , que es la única componente que afecta la duración del día solar. Un ejemplo práctico de oblicuidad es que el desplazamiento diario de la sombra proyectada por el Sol en un reloj de sol, incluso en el ecuador, es menor cerca de los solsticios y mayor cerca de los equinoccios. Si este efecto operara solo, entonces los días durarían hasta 24 horas y 20,3 segundos (medidos desde el mediodía solar hasta el mediodía solar) cerca de los solsticios, y hasta 20,3 segundos más cortos que 24 horas cerca de los equinoccios. [20] [23] [22]
En la figura de la derecha podemos ver la variación mensual de la pendiente aparente del plano de la eclíptica al mediodía solar visto desde la Tierra. Esta variación se debe a la aparente precesión de la Tierra en rotación a lo largo del año, vista desde el Sol durante el mediodía solar.
En términos de la ecuación del tiempo, la inclinación de la eclíptica resulta en la contribución de una variación de onda sinusoidal con:
Este componente de la EoT está representado por el factor "b" antes mencionado:
Los dos factores mencionados anteriormente tienen diferentes longitudes de onda, amplitudes y fases, por lo que su contribución combinada es una onda irregular. En la época 2000 estos son los valores (en minutos y segundos con fechas UT ):
[ cita necesaria ]
En escalas de tiempo más cortas (miles de años), los cambios en las fechas del equinoccio y el perihelio serán más importantes. El primero es causado por la precesión y desplaza el equinoccio hacia atrás en comparación con las estrellas. Pero puede ignorarse en la discusión actual, ya que nuestro calendario gregoriano está construido de tal manera que mantiene la fecha del equinoccio de primavera en el 20 de marzo (al menos con suficiente precisión para nuestro objetivo aquí). El desplazamiento del perihelio es hacia adelante, aproximadamente 1,7 días cada siglo. En 1246, el perihelio ocurrió el 22 de diciembre, el día del solsticio, por lo que las dos ondas contribuyentes tenían puntos cero comunes y la ecuación de la curva de tiempo era simétrica: en Algoritmos astronómicos, Meeus da extremos de febrero y noviembre de 15 m 39 s y mayo y Los de julio de 4 m 58 s. Antes de eso, el mínimo de febrero era mayor que el máximo de noviembre, y el máximo de mayo era mayor que el mínimo de julio. De hecho, en años anteriores a -1900 (1901 a. C.), el máximo de mayo fue mayor que el máximo de noviembre. En el año −2000 (2001 a. C.), el máximo de mayo fue de +12 minutos y un par de segundos, mientras que el máximo de noviembre fue de poco menos de 10 minutos. El cambio secular es evidente cuando se compara una gráfica actual de la ecuación del tiempo (ver más abajo) con una de hace 2000 años, por ejemplo, una construida a partir de los datos de Ptolomeo. [25]

Si el gnomon (el objeto que proyecta la sombra) no es un borde sino un punto (por ejemplo, un agujero en un plato), la sombra (o punto de luz) trazará una curva durante el transcurso de un día. Si la sombra se proyecta sobre una superficie plana, esta curva será una sección cónica (generalmente una hipérbola), ya que el círculo del movimiento del Sol junto con el punto gnomon definen un cono. En los equinoccios de primavera y otoño, el cono degenera en un plano y la hipérbola en una línea. Con una hipérbola diferente para cada día, se pueden poner marcas horarias en cada hipérbola que incluyen las correcciones necesarias. Desafortunadamente, cada hipérbola corresponde a dos días diferentes, uno en cada mitad del año, y estos dos días requerirán correcciones diferentes. Un compromiso conveniente es trazar la línea para el "tiempo medio" y agregar una curva que muestre la posición exacta de los puntos de sombra al mediodía durante el transcurso del año. Esta curva tomará la forma de un ocho y se conoce como analema . Comparando el analema con la línea media del mediodía, se puede determinar la cantidad de corrección que se aplicará generalmente ese día.
La ecuación del tiempo se utiliza no sólo en relación con los relojes de sol y dispositivos similares, sino también para muchas aplicaciones de la energía solar . Máquinas como los seguidores solares y los helióstatos tienen que moverse de maneras que están influenciadas por la ecuación del tiempo.
La hora civil es la hora media local de un meridiano que a menudo pasa cerca del centro de la zona horaria y que posiblemente pueda verse alterada aún más por el horario de verano . Cuando se desea encontrar el tiempo solar aparente que corresponde a un tiempo civil determinado, se debe considerar la diferencia de longitud entre el sitio de interés y el meridiano de la zona horaria, el horario de verano y la ecuación del tiempo. [26]
La ecuación del tiempo se obtiene de una tabla publicada o de un gráfico. Para fechas del pasado, dichas tablas se elaboran a partir de mediciones históricas o mediante cálculos; para fechas futuras, por supuesto, sólo se pueden calcular tablas. En dispositivos como los helióstatos controlados por computadora, la computadora suele estar programada para calcular la ecuación del tiempo. El cálculo puede ser numérico o analítico. Los primeros se basan en la integración numérica de las ecuaciones diferenciales del movimiento, incluidos todos los efectos gravitacionales y relativistas significativos. Los resultados tienen una precisión superior a 1 segundo y son la base de los datos de almanaque modernos. Estos últimos se basan en una solución que incluye sólo la interacción gravitacional entre el Sol y la Tierra, más simple que la primera, pero no tan precisa. Su precisión se puede mejorar incluyendo pequeñas correcciones.
La siguiente discusión describe un algoritmo razonablemente preciso (que coincide con los datos del almanaque con un margen de error de 3 segundos en un amplio rango de años) para la ecuación del tiempo que es bien conocido por los astrónomos. [27] : 89 También muestra cómo obtener una fórmula aproximada simple (con una precisión de 1 minuto en un intervalo de tiempo grande), que se puede evaluar fácilmente con una calculadora y proporciona una explicación simple del fenómeno que se usó anteriormente en este artículo.
La definición precisa de la ecuación del tiempo es [28] : 1529
Las cantidades que aparecen en esta ecuación son
Aquí el tiempo y el ángulo son cantidades que están relacionadas por factores como: 2 π radianes = 360° = 1 día = 24 horas. La diferencia, EOT, es mensurable ya que GHA es un ángulo que se puede medir y el Tiempo Universal , UT, es una escala para medir el tiempo. El desplazamiento de π = 180° = 12 horas desde UT es necesario porque UT es cero a la medianoche media mientras que GMHA = 0 al mediodía medio. [n 6] Tanto GHA como GMHA, como todos los ángulos físicos, tienen una discontinuidad matemática, pero no física, en su respectivo mediodía (aparente y medio). A pesar de las discontinuidades matemáticas de sus componentes, EOT se define como una función continua sumando (o restando) 24 horas en el pequeño intervalo de tiempo entre las discontinuidades en GHA y GMHA.
Según las definiciones de los ángulos en la esfera celeste GHA = GAST − α (ver ángulo horario )
donde:
Al sustituir en la ecuación del tiempo, es
Al igual que la fórmula anterior para GHA, se puede escribir GMHA = GAST − α M , donde el último término es la ascensión recta del Sol medio. La ecuación a menudo se escribe en estos términos como [4] : 275 [30] : 45
donde α M = GAST − UT + desplazamiento . En esta formulación, una medición o cálculo de EOT en un cierto valor de tiempo depende de una medición o cálculo de α en ese momento. Tanto α como α M varían de 0 a 24 horas en el transcurso de un año. El primero tiene una discontinuidad en un momento que depende del valor de UT, mientras que el segundo la tiene en un momento ligeramente posterior. Como consecuencia, cuando se calcula de esta manera EOT tiene dos discontinuidades artificiales. Ambos pueden eliminarse restando 24 horas del valor de EOT en el pequeño intervalo de tiempo después de la discontinuidad en α y antes de la de α M. El EOT resultante es una función continua del tiempo.
Otra definición, denominada E para distinguirla de EOT, es
Aquí GMST = GAST − eqeq , es el tiempo sidéreo medio de Greenwich (el ángulo entre el equinoccio de primavera medio y el Sol medio en el plano del ecuador). Por tanto, GMST es una aproximación a GAST (y E es una aproximación a EOT); eqeq se llama ecuación de los equinoccios y se debe al bamboleo o nutación del eje de rotación de la Tierra alrededor de su movimiento de precesión. Dado que la amplitud del movimiento nutacional es sólo de aproximadamente 1,2 s (18 ″ de longitud), la diferencia entre EOT y E puede ignorarse a menos que uno esté interesado en una precisión de menos de un segundo.
Una tercera definición, denotada como Δ t para distinguirla de EOT y E , y ahora llamada Ecuación del Tiempo de Efemérides [28] : 1532 (antes de la distinción que ahora se hace entre EOT, E y Δ t, esta última se conocía como la ecuación del tiempo) es
aquí Λ es la longitud de la eclíptica del Sol medio (el ángulo entre el equinoccio de primavera medio y el Sol medio en el plano de la eclíptica ).
La diferencia Λ − (GMST − UT + offset) es de 1,3 s entre 1960 y 2040. Por lo tanto, en este rango restringido de años, Δ t es una aproximación al EOT cuyo error está en el rango de 0,1 a 2,5 s dependiendo de la corrección de longitud en la ecuación de los equinoccios; Para muchos propósitos, por ejemplo para corregir un reloj de sol, esta precisión es más que suficiente.
La ascensión recta, y por tanto la ecuación del tiempo, se puede calcular a partir de la teoría del movimiento celeste de dos cuerpos de Newton, en la que los cuerpos (la Tierra y el Sol) describen órbitas elípticas alrededor de su centro de masa común. Usando esta teoría, la ecuación del tiempo se convierte en
donde están los nuevos ángulos que aparecen
Para completar el cálculo se requieren tres ángulos adicionales:
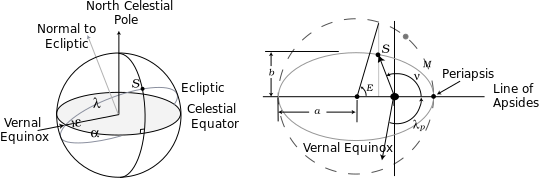
Todos estos ángulos se muestran en la figura de la derecha, que muestra la esfera celeste y la órbita elíptica del Sol vista desde la Tierra (la misma que la órbita de la Tierra vista desde el Sol). En esta figura ε es la oblicuidad , mientras que e = √ 1 − ( b / a ) 2 es la excentricidad de la elipse.
Ahora dado un valor de 0 ≤ M ≤ 2π , se puede calcular α ( M ) mediante el siguiente procedimiento bien conocido: [27] : 89
Primero, dada M , calcule E a partir de la ecuación de Kepler : [31] : 159
Aunque esta ecuación no se puede resolver exactamente en forma cerrada, los valores de E ( M ) se pueden obtener a partir de series infinitas (potenciales o trigonométricas), métodos gráficos o numéricos. Alternativamente, tenga en cuenta que para e = 0 , E = M , y por iteración: [32] : 2
Esta aproximación se puede mejorar, para e pequeña , iterando nuevamente,
y la iteración continua produce términos de orden sucesivamente superior de la expansión de la serie de potencias en e . Para valores pequeños de e (mucho menores que 1), dos o tres términos de la serie dan una buena aproximación para E ; cuanto más pequeña e , mejor será la aproximación.
Luego, conociendo E , calcule la verdadera anomalía ν a partir de una relación de órbita elíptica [31] : 165
La rama correcta de la función de valores múltiples arctan x a usar es la que hace de ν una función continua de E ( M ) a partir de ν E =0 = 0 . Por lo tanto, para 0 ≤ E < π use arctan x = arctan x , y para π < E ≤ 2π use arctan x = arctan x + π . En el valor específico E = π para el cual el argumento de tan es infinito, use ν = E. Aquí arctan x es la rama principal, | arctán x | <π/2; la función que devuelven las calculadoras y las aplicaciones informáticas. Alternativamente, esta función se puede expresar en términos de su serie de Taylor en e , cuyos primeros tres términos son:
Para e pequeña esta aproximación (o incluso sólo los dos primeros términos) es buena. Combinando la aproximación para E ( M ) con esta para ν ( E ) produce
La relación ν ( M ) se llama ecuación del centro ; la expresión escrita aquí es una aproximación de segundo orden en e . Para el pequeño valor de e que caracteriza la órbita de la Tierra, esto proporciona una muy buena aproximación para ν ( M ) .
A continuación, conociendo ν , calcule λ a partir de su definición:
El valor de λ varía de forma no lineal con M porque la órbita es elíptica y no circular. De la aproximación para ν :
Finalmente, conociendo λ , calcule α a partir de una relación para el triángulo rectángulo en la esfera celeste que se muestra arriba [33] : 22
Tenga en cuenta que el cuadrante de α es el mismo que el de λ , por lo tanto reduzca λ al rango de 0 a 2 π y escriba
donde k es 0 si λ está en el cuadrante 1, es 1 si λ está en los cuadrantes 2 o 3 y es 2 si λ está en el cuadrante 4. Para los valores en los que tan es infinito, α = λ .
Aunque se pueden obtener valores aproximados para α a partir de series de Taylor truncadas como las de ν , [34] : 32 es más eficaz utilizar la ecuación [35] : 374
donde y = tan 2 (ε/2) . Tenga en cuenta que para ε = y = 0 , α = λ e iterando dos veces:
La ecuación del tiempo se obtiene sustituyendo el resultado del cálculo de la ascensión recta en una fórmula de ecuación del tiempo. Aquí se utiliza Δ t ( M ) = M + λ p − α [ λ ( M )] ; en parte porque no se incluyen pequeñas correcciones (del orden de 1 segundo), que justificarían el uso de E , y en parte porque el objetivo es obtener una expresión analítica simple. El uso de aproximaciones de dos términos para λ ( M ) y α ( λ ) permite escribir Δ t como una expresión explícita de dos términos, que se denomina Δ t ey porque es una aproximación de primer orden en e y en y .
Esta ecuación fue deducida por primera vez por Milne, [35] : 375, quien la escribió en términos de λ = M + λ p . Los valores numéricos escritos aquí resultan del uso de los valores de los parámetros orbitales, e =0,016 709 , ε =23,4393 °=0,409 093 radianes, y λ p =282,9381 ° =4.938 201 radianes que corresponden a la época del 1 de enero de 2000 a las 12 horas UT1 . Al evaluar la expresión numérica para Δ t ey como se indicó anteriormente, una calculadora debe estar en modo radianes para obtener los valores correctos porque el valor de 2 λ p − 2π en el argumento del segundo término está escrito allí en radianes. También se pueden escribir aproximaciones de orden superior, [36] : Ecuaciones (45) y (46) , pero necesariamente tienen más términos. Por ejemplo, la aproximación de segundo orden tanto en e como en y consta de cinco términos [28] : 1535
Esta aproximación tiene el potencial de lograr una alta precisión; sin embargo, para lograrla en un amplio rango de años, se debe permitir que los parámetros e , ε y λ p varíen con el tiempo. [27] : 86 [28] : 1531,1535 Esto crea complicaciones de cálculo adicionales. Se han propuesto otras aproximaciones, por ejemplo, Δ t e [27] : 86 [37] que usa la ecuación de primer orden del centro pero ninguna otra aproximación para determinar α , y Δ t e 2 [38] que usa la ecuación de segundo orden ecuación del centro.
La variable de tiempo, M , se puede escribir en términos de n , el número de días después del perihelio, o D , el número de días después de una fecha y hora específicas (época):

Aquí M D es el valor de M en la fecha y hora elegidas. Para los valores dados aquí, en radianes, M D es el medido para el Sol real en la época, el 1 de enero de 2000 a las 12 del mediodía UT1, y D es el número de días después de esa época. En el periapsis M = 2π , por lo que al resolver se obtiene D = D p =2.508 109 . Esto sitúa la periapsis el 4 de enero de 2000 a las 00:11:41 mientras que la periapsis real es, según los resultados del Multiyear Interactive Computer Almanac [39] (abreviado como MICA), el 3 de enero de 2000 a las 05:17:30. Esta gran discrepancia se debe a que la diferencia entre el radio orbital en las dos ubicaciones es sólo de 1 parte en un millón; en otras palabras, el radio es una función muy débil del tiempo cerca del periapsis. Como cuestión práctica, esto significa que no se puede obtener un resultado muy preciso para la ecuación del tiempo utilizando n y sumando la fecha real del periapsis para un año determinado. Sin embargo, se puede lograr una alta precisión utilizando la formulación en términos de D.
Cuando D > D p , M es mayor que 2 π y hay que restarle un múltiplo de 2 π (que depende del año) para llevarlo al rango de 0 a 2 π . Asimismo, para los años anteriores al 2000 se deben sumar múltiplos de 2 π . Por ejemplo, para el año 2010, D varía de3653 el 1 de enero al mediodía hasta4017 el 31 de diciembre al mediodía; los valores M correspondientes son69.078 9468 y75,340 4748 y se reducen al rango de 0 a 2 π restando 10 y 11 veces 2 π respectivamente.
Siempre se puede escribir:
5) D = n Y + d
dónde:
La ecuación resultante para los años posteriores al 2000, escrita como la suma de dos términos, dados 1), 4) y 5), es:
6 minutos]
En formato de texto plano:
7) EoT = -7,659sin(6,24004077 + 0,01720197(365*(y-2000) + d)) + 9,863sin( 2 (6,24004077 + 0,01720197 (365*(y-2000) + d)) + 3,5932 ) [minutos]
El término "a" representa la contribución de la excentricidad, el término "b" representa la contribución de la oblicuidad.
El resultado de los cálculos generalmente se presenta como un conjunto de valores tabulares o como una gráfica de la ecuación del tiempo en función de d . En la figura se muestra una comparación de los gráficos de Δ t , Δ t ey y los resultados de MICA, todos para el año 2000. Se considera que la gráfica de Δ t ey está cerca de los resultados producidos por MICA, el error absoluto, Err = | Δ t ey − MICA2000 | , es inferior a 1 minuto durante todo el año; su valor más grande es 43,2 segundos y ocurre el día 276 (3 de octubre). La gráfica de Δ t es indistinguible de los resultados de MICA; el error absoluto más grande entre los dos es de 2,46 s el día 324 (20 de noviembre).
Para elegir la rama apropiada de la relación arctan con respecto a la continuidad de la función, es útil una versión modificada de la función arctangente. Aporta conocimientos previos sobre el valor esperado por un parámetro. La función arcotangente modificada se define como:
Produce un valor lo más cercano posible a η . La función round redondea al número entero más cercano.
Aplicando esto se obtiene:
El parámetro M + λ p se dispone aquí a fijar Δ t al valor cero más cercano al deseado.
La diferencia entre los resultados de MICA y Δ t se verificó cada 5 años en el rango de 1960 a 2040. En todos los casos, el error absoluto máximo fue inferior a 3 s; la mayor diferencia, 2,91 s, se produjo el 22 de mayo de 1965 (día 141). Sin embargo, para lograr este nivel de precisión en este rango de años es necesario tener en cuenta el cambio secular en los parámetros orbitales con el tiempo. Las ecuaciones que describen esta variación son: [27] : 86 [28] : 1531,1535
Según estas relaciones, en 100 años ( D = 36 525 ), λ p aumenta aproximadamente un 0,5 % (1,7°), e disminuye aproximadamente un 0,25 % y ε disminuye aproximadamente un 0,05 %.
Como resultado, la cantidad de cálculos necesarios para cualquiera de las aproximaciones de orden superior de la ecuación del tiempo requiere una computadora para completarlos, si se quiere lograr su precisión inherente en un amplio rango de tiempo. En este caso, evaluar Δ t usando una computadora no es más difícil que cualquiera de sus aproximaciones.
En todo esto, tenga en cuenta que Δ t ey , como se escribió anteriormente, es fácil de evaluar, incluso con una calculadora, es lo suficientemente preciso (mejor que 1 minuto en el rango de 80 años) para corregir relojes de sol y tiene una buena explicación física como la suma de dos términos, uno debido a oblicuidad y otro a excentricidad que se utilizó anteriormente en el artículo. Esto no es cierto ni para Δ t considerado como función de M ni para cualquiera de sus aproximaciones de orden superior.
Otro procedimiento para calcular la ecuación del tiempo se puede realizar de la siguiente manera. [37] Los ángulos están en grados; Se aplica el orden convencional de operaciones .
donde n es la velocidad orbital angular media de la Tierra en grados por día, también conocida como "el movimiento diario medio" .
donde D es la fecha, contada en días a partir del 1 del 1 de enero (es decir, los días que forman parte de la fecha ordinal del año). 9 es el número aproximado de días desde el solsticio de diciembre hasta el 31 de diciembre. A es el ángulo que adoptaría la Tierra en su órbita a su velocidad media desde el solsticio de diciembre hasta la fecha D.
B es el ángulo en que la Tierra se mueve desde el solsticio hasta la fecha D , incluida una corrección de primer orden para la excentricidad orbital de la Tierra, 0,0167. El número 3 es el número aproximado de días desde el 31 de diciembre hasta la fecha actual del perihelio terrestre . Esta expresión para B se puede simplificar combinando constantes para:
Aquí, C es la diferencia entre el ángulo movido a la velocidad media y el ángulo a la velocidad corregida proyectado sobre el plano ecuatorial, y dividido por 180° para obtener la diferencia en " medias vueltas ". El valor 23,44° es la inclinación del eje de la Tierra ("oblicuidad") . La resta da el signo convencional a la ecuación del tiempo. Para cualquier valor dado de x , arctan x (a veces escrito como tan −1 x ) tiene múltiples valores, que se diferencian entre sí por números enteros de medias vueltas. El valor generado por una calculadora o computadora puede no ser el apropiado para este cálculo. Esto puede hacer que C se equivoque en un número entero de medias vueltas. Las medias vueltas sobrantes se eliminan en el siguiente paso del cálculo para obtener la ecuación del tiempo:
La expresión nint( C ) significa el número entero más cercano a C . En una computadora, se puede programar, por ejemplo, como INT(C + 0.5) . Su valor es 0, 1 o 2 en diferentes épocas del año. Al restarlo queda un pequeño número fraccionario positivo o negativo de medias vueltas, que se multiplica por 720, el número de minutos (12 horas) que tarda la Tierra en girar media vuelta con respecto al Sol, para obtener la ecuación del tiempo.
En comparación con los valores publicados, [8] este cálculo tiene un error cuadrático medio de sólo 3,7 s. El mayor error es de 6,0 s. Esto es mucho más preciso que la aproximación descrita anteriormente, pero no tan preciso como el cálculo elaborado.
El valor de B en el cálculo anterior es un valor preciso para la longitud de la eclíptica del Sol (desplazada 90°), por lo que la declinación solar δ queda fácilmente disponible:
lo cual tiene una precisión de una fracción de grado.