Curvatura

Medida matemática de cuánto se desvía una curva o superficie de la planitud.

Célula migratoria de tipo salvaje de Dictyostelium discoideum cuyo límite está coloreado por la curvatura. Barra de escala: 5 μm.

En matemáticas , la curvatura es uno de varios conceptos fuertemente relacionados en geometría que miden intuitivamente la cantidad en la que una curva se desvía de ser una línea recta o en la que una superficie se desvía de ser un plano . Si una curva o superficie está contenida en un espacio más grande, la curvatura se puede definir extrínsecamente en relación con el espacio circundante. La curvatura de las variedades de Riemann de dimensión al menos dos se puede definir intrínsecamente sin referencia a un espacio más grande.

En el caso de las curvas, el ejemplo canónico es el de un círculo , que tiene una curvatura igual al recíproco de su radio . Los círculos más pequeños se curvan más bruscamente y, por lo tanto, tienen una curvatura mayor. La curvatura en un punto de una curva diferenciable es la curvatura de su círculo osculador , es decir, el círculo que mejor se aproxima a la curva cerca de este punto. La curvatura de una línea recta es cero. A diferencia de la tangente , que es una cantidad vectorial, la curvatura en un punto es típicamente una cantidad escalar , es decir, se expresa mediante un único número real .

Para las superficies (y, más generalmente, para las variedades de dimensiones superiores ) que están insertas en un espacio euclidiano , el concepto de curvatura es más complejo, ya que depende de la elección de una dirección en la superficie o la variedad. Esto conduce a los conceptos de curvatura máxima , curvatura mínima y curvatura media .

Historia

En el Tractatus de configurationibus qualitatum et motuum, ^[1] el filósofo y matemático del siglo XIV Nicole Oresme introduce el concepto de curvatura como medida de desviación de la rectitud; para los círculos, considera que la curvatura es inversamente proporcional al radio; e intenta extender esta idea a otras curvas como una magnitud que varía continuamente. ^[2]

La curvatura de una curva diferenciable se definió originalmente a través de círculos osculadores . En este contexto, Augustin-Louis Cauchy demostró que el centro de curvatura es el punto de intersección de dos líneas normales infinitamente cercanas a la curva. ^[3] curva

Curvas planas

Intuitivamente, la curvatura describe para cualquier parte de una curva cuánto cambia la dirección de la curva sobre una pequeña distancia recorrida (por ejemplo, ángulo en rad/m ), por lo que es una medida de la tasa instantánea de cambio de dirección de un punto que se mueve en la curva: cuanto mayor es la curvatura, mayor es esta tasa de cambio. En otras palabras, la curvatura mide qué tan rápido gira el vector tangente unitario a la curva en el punto p ^[4] cuando el punto p se mueve a una velocidad unitaria a lo largo de la curva. De hecho, se puede demostrar que esta tasa instantánea de cambio es exactamente la curvatura. Más precisamente, supongamos que el punto se mueve en la curva a una velocidad constante de una unidad, es decir, la posición del punto P ( s ) es una función del parámetro s , que puede pensarse como el tiempo o como la longitud del arco desde un origen dado. Sea T ( s ) un vector tangente unitario de la curva en P ( s ) , que también es la derivada de P ( s ) con respecto a s . Entonces, la derivada de T ( s ) con respecto a s es un vector que es normal a la curva y cuya longitud es la curvatura.

Para ser significativa, la definición de la curvatura y sus diferentes caracterizaciones requieren que la curva sea continuamente diferenciable cerca de P , por tener una tangente que varía continuamente; requiere también que la curva sea dos veces diferenciable en P , para asegurar la existencia de los límites involucrados y de la derivada de T ( s ) .

La caracterización de la curvatura en términos de la derivada del vector tangente unitario es probablemente menos intuitiva que la definición en términos del círculo osculador, pero las fórmulas para calcular la curvatura son más fáciles de deducir. Por lo tanto, y también debido a su uso en cinemática , esta caracterización se da a menudo como una definición de la curvatura.

Círculo osculador

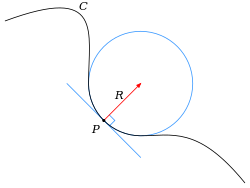
Históricamente, la curvatura de una curva diferenciable se definía a través del círculo osculador , que es el círculo que mejor se aproxima a la curva en un punto. Más precisamente, dado un punto P en una curva, cada otro punto Q de la curva define un círculo (o a veces una línea) que pasa por Q y es tangente a la curva en P. El círculo osculador es el límite , si existe, de este círculo cuando Q tiende a P. Entonces, el centro y el radio de curvatura de la curva en P son el centro y el radio del círculo osculador. La curvatura es el recíproco del radio de curvatura. Es decir, la curvatura es

${\displaystyle \kappa ={\frac {1}{R}},}$

donde R es el radio de curvatura ^[5] (todo el círculo tiene esta curvatura, se puede leer como un giro de 2π sobre la longitud 2π R ).

Esta definición es difícil de manipular y de expresar en fórmulas, por lo que se han introducido otras definiciones equivalentes.

En términos de parametrización de longitud de arco

Toda curva diferenciable puede parametrizarse con respecto a la longitud del arco . ^[6] En el caso de una curva plana, esto significa la existencia de una parametrización γ ( s ) = ( x ( s ), y ( s )) , donde x e y son funciones diferenciables de valor real cuyas derivadas satisfacen

${\displaystyle \|{\boldsymbol {\gamma }}'\|={\sqrt {x'(s)^{2}+y'(s)^{2}}}=1.}$

Esto significa que el vector tangente

${\displaystyle \mathbf {T} (s)={\bigl (}x'(s),y'(s){\bigr )}}$

tiene una longitud igual a uno y por lo tanto es un vector tangente unitario .

Si la curva es dos veces diferenciable, es decir, si existen las segundas derivadas de x e y , entonces existe la derivada de T ( s ) . Este vector es normal a la curva, su longitud es la curvatura κ ( s ) y está orientado hacia el centro de curvatura. Es decir,

${\displaystyle {\begin{aligned}\mathbf {T} (s)&={\boldsymbol {\gamma }}'(s),\\[8mu]\|\mathbf {T} (s)\|^{2}&=1\ {\text{(constant)}}\implies \mathbf {T} '(s)\cdot \mathbf {T} (s)=0,\\[5mu]\kappa (s)&=\|\mathbf {T} '(s)\|=\|{\boldsymbol {\gamma }}''(s)\|={\sqrt {x''(s)^{2}+y''(s)^{2}}}\end{aligned}}}$

Además, debido a que el radio de curvatura es (suponiendo que 𝜿 ( s ) ≠ 0)

${\displaystyle R(s)={\frac {1}{\kappa (s)}},}$

y el centro de curvatura está en la normal a la curva, el centro de curvatura es el punto

${\displaystyle \mathbf {C} (s)={\boldsymbol {\gamma }}(s)+{\frac {1}{\kappa (s)^{2}}}\mathbf {T} '(s).}$

(En caso de que la curvatura sea cero, el centro de curvatura no está ubicado en ningún lugar del plano R ² y a menudo se dice que está ubicado "en el infinito".)

Si N ( s ) es el vector normal unitario obtenido de T ( s ) mediante una rotación en sentido antihorario de ⁠π/2⁠ , entonces

${\displaystyle \mathbf {T} '(s)=k(s)\mathbf {N} (s),}$

con k ( s ) = ± κ ( s ) . El número real k ( s ) se llama curvatura orientada o curvatura con signo . Depende tanto de la orientación del plano (definición de sentido antihorario) como de la orientación de la curva proporcionada por la parametrización. De hecho, el cambio de variable s → – s proporciona otra parametrización de longitud de arco y cambia el signo de k ( s ) .

En términos de una parametrización general

Sea γ ( t ) = ( x ( t ), y ( t )) una representación paramétrica propia de una curva plana dos veces diferenciable. Aquí, propia significa que en el dominio de definición de la parametrización, la derivada ⁠dγ​/es⁠ está definido, es diferenciable y en ninguna parte es igual al vector cero.

Con tal parametrización, la curvatura firmada es

${\displaystyle k={\frac {x'y''-y'x''}{{\bigl (}{x'}^{2}+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},}$

donde los primos se refieren a las derivadas con respecto a t . La curvatura κ es entonces

${\displaystyle \kappa ={\frac {\left|x'y''-y'x''\right|}{{\bigl (}{x'}^{2}+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}.}$

Estos se pueden expresar de forma libre de coordenadas como

${\displaystyle k={\frac {\det \left({\boldsymbol {\gamma }}',{\boldsymbol {\gamma }}''\right)}{\|{\boldsymbol {\gamma }}'\|^{3}}},\qquad \kappa ={\frac {\left|\det \left({\boldsymbol {\gamma }}',{\boldsymbol {\gamma }}''\right)\right|}{\|{\boldsymbol {\gamma }}'\|^{3}}}.}$

Estas fórmulas se pueden derivar del caso especial de parametrización de la longitud de arco de la siguiente manera. La condición anterior sobre la parametrización implica que la longitud de arco s es una función monótona diferenciable del parámetro t , y a la inversa, que t es una función monótona de s . Además, cambiando, si es necesario, s por – s , se puede suponer que estas funciones son crecientes y tienen una derivada positiva. Usando la notación de la sección anterior y la regla de la cadena , se tiene

${\displaystyle {\frac {d{\boldsymbol {\gamma }}}{dt}}={\frac {ds}{dt}}\mathbf {T} ,}$

y así, tomando la norma de ambos lados

${\displaystyle {\frac {dt}{ds}}={\frac {1}{\|{\boldsymbol {\gamma }}'\|}},}$

donde la prima denota diferenciación con respecto a t .

La curvatura es la norma de la derivada de T con respecto a s . Al utilizar la fórmula anterior y la regla de la cadena, esta derivada y su norma se pueden expresar en términos de γ ′ y γ ″ solamente, con el parámetro de longitud de arco s completamente eliminado, lo que da las fórmulas anteriores para la curvatura.

Gráfica de una función

La gráfica de una función y = f ( x ) , es un caso especial de una curva parametrizada, de la forma

${\displaystyle {\begin{aligned}x&=t\\y&=f(t).\end{aligned}}}$

Como las derivadas primera y segunda de x son 1 y 0, las fórmulas anteriores se simplifican a

${\displaystyle \kappa ={\frac {\left|y''\right|}{{\bigl (}1+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},}$

para la curvatura, y para

${\displaystyle k={\frac {y''}{{\bigl (}1+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},}$

para la curvatura firmada.

En el caso general de una curva, el signo de la curvatura con signo es algo arbitrario, ya que depende de la orientación de la curva. En el caso del gráfico de una función, existe una orientación natural al aumentar los valores de x . Esto hace que el signo de la curvatura con signo sea significativo.

El signo de la curvatura con signo es el mismo que el signo de la segunda derivada de f . Si es positivo, el gráfico tiene una concavidad hacia arriba y, si es negativo, el gráfico tiene una concavidad hacia abajo. Si es cero, entonces se tiene un punto de inflexión o un punto de ondulación .

Cuando la pendiente del gráfico (es decir, la derivada de la función) es pequeña, la curvatura con signo se aproxima bien mediante la segunda derivada. Más precisamente, utilizando la notación O mayúscula , se tiene

${\displaystyle k(x)=y''{\Bigl (}1+O{\bigl (}{\textstyle y'}^{2}{\bigr )}{\Bigr )}.}$

En física e ingeniería es habitual aproximar la curvatura con la segunda derivada, por ejemplo, en la teoría de vigas o para derivar la ecuación de onda de una cuerda bajo tensión y otras aplicaciones en las que intervienen pendientes pequeñas. Esto permite a menudo tratar sistemas que de otro modo serían no lineales como si fueran aproximadamente lineales.

Coordenadas polares

Si una curva se define en coordenadas polares por el radio expresado en función del ángulo polar, es decir r es una función de θ , entonces su curvatura es

${\displaystyle \kappa (\theta )={\frac {\left|r^{2}+2{r'}^{2}-r\,r''\right|}{{\bigl (}r^{2}+{r'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}}$

donde el primo se refiere a la diferenciación con respecto a θ .

Esto resulta de la fórmula para parametrizaciones generales, considerando la parametrización

${\displaystyle {\begin{aligned}x&=r(\theta )\cos \theta \\y&=r(\theta )\sin \theta \end{aligned}}}$

Curva implícita

Para una curva definida por una ecuación implícita F ( x , y ) = 0 con derivadas parciales denotadas F _x , F _y , F _xx , F _xy , F _yy , la curvatura está dada por ^[7]

${\displaystyle \kappa ={\frac {\left|F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}\right|}{{\bigl (}F_{x}^{2}+F_{y}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}.}$

La curvatura con signo no está definida, ya que depende de una orientación de la curva que no está prevista en la ecuación implícita. Nótese que cambiar F por – F no cambiaría la curva definida por F ( x , y ) = 0 , pero sí cambiaría el signo del numerador si se omitiera el valor absoluto en la fórmula anterior.

Un punto de la curva donde F _x = F _y = 0 es un punto singular , lo que significa que la curva no es diferenciable en este punto y, por lo tanto, la curvatura no está definida (la mayoría de las veces, el punto es un punto de cruce o una cúspide ).

La fórmula anterior para la curvatura se puede derivar de la expresión de la curvatura del gráfico de una función utilizando el teorema de función implícita y el hecho de que, en dicha curva, se tiene

${\displaystyle {\frac {dy}{dx}}=-{\frac {F_{x}}{F_{y}}}.}$

Ejemplos

Puede ser útil verificar con ejemplos sencillos que las diferentes fórmulas dadas en las secciones anteriores dan el mismo resultado.

Círculo

Una parametrización común de un círculo de radio r es γ ( t ) = ( r cos t , r sin t ) . La fórmula para la curvatura da

${\displaystyle k(t)={\frac {r^{2}\sin ^{2}t+r^{2}\cos ^{2}t}{{\bigl (}r^{2}\cos ^{2}t+r^{2}\sin ^{2}t{\bigr )}{\vphantom {'}}^{3/2}}}={\frac {1}{r}}.}$

Se deduce, como se esperaba, que el radio de curvatura es el radio del círculo y que el centro de curvatura es el centro del círculo.

El círculo es un caso raro en el que la parametrización de la longitud del arco es fácil de calcular, ya que es

${\displaystyle {\boldsymbol {\gamma }}(s)=\left(r\cos {\frac {s}{r}},\,r\sin {\frac {s}{r}}\right).}$

Se trata de una parametrización de longitud de arco, ya que la norma de

${\displaystyle {\boldsymbol {\gamma }}'(s)=\left(-\sin {\frac {s}{r}},\,\cos {\frac {s}{r}}\right)}$

es igual a uno. Esta parametrización da el mismo valor para la curvatura, ya que equivale a dividir por r ³ tanto en el numerador como en el denominador de la fórmula anterior.

El mismo círculo también se puede definir mediante la ecuación implícita F ( x , y ) = 0 con F ( x , y ) = x ² + y ² – r ² . Entonces, la fórmula para la curvatura en este caso da

${\displaystyle {\begin{aligned}\kappa &={\frac {\left|F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}\right|}{{\bigl (}F_{x}^{2}+F_{y}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}\\&={\frac {8y^{2}+8x^{2}}{{\bigl (}4x^{2}+4y^{2}{\bigr )}{\vphantom {'}}^{3/2}}}\\&={\frac {8r^{2}}{{\bigl (}4r^{2}{\bigr )}{\vphantom {'}}^{3/2}}}={\frac {1}{r}}.\end{aligned}}}$

Parábola

Considere la parábola y = ax ² + bx + c .

Es la gráfica de una función, con derivada 2 ax + b , y segunda derivada 2 a . Por lo tanto, la curvatura con signo es

${\displaystyle k(x)={\frac {2a}{{\bigl (}1+\left(2ax+b\right)^{2}{\bigr )}{\vphantom {)}}^{3/2}}}.}$

Tiene el signo a para todos los valores de x . Esto significa que, si a > 0 , la concavidad está dirigida hacia arriba en todas partes; si a < 0 , la concavidad está dirigida hacia abajo; para a = 0 , la curvatura es cero en todas partes, lo que confirma que la parábola degenera en una línea en este caso.

La curvatura (sin signo) es máxima para x = – ⁠b/2 un⁠ , es decir en el punto estacionario (derivada cero) de la función, que es el vértice de la parábola.

Considere la parametrización γ ( t ) = ( t , at ² + bt + c ) = ( x , y ) . La primera derivada de x es 1 y la segunda derivada es cero. Sustituyendo en la fórmula para parametrizaciones generales se obtiene exactamente el mismo resultado que el anterior, con x reemplazado por t . Si usamos primos para las derivadas con respecto al parámetro t .

La misma parábola también puede definirse mediante la ecuación implícita F ( x , y ) = 0 con F ( x , y ) = ax ² + bx + c – y . Como F _y = –1 , y F _yy = F _xy = 0 , se obtiene exactamente el mismo valor para la curvatura (sin signo). Sin embargo, la curvatura con signo no tiene sentido aquí, ya que – F ( x , y ) = 0 es una ecuación implícita válida para la misma parábola, que da el signo opuesto para la curvatura.

Fórmulas de Frenet-Serret para curvas planas

Los vectores T y N en dos puntos de una curva plana, una versión trasladada del segundo marco (punteado), y δ T el cambio en T . Aquí δs es la distancia entre los puntos. En el límite ⁠el T/ds⁠ estará en la dirección N. La curvatura describe la velocidad de rotación del marco.

La expresión de la curvatura en términos de parametrización de la longitud de arco es esencialmente la primera fórmula de Frenet-Serret

${\displaystyle \mathbf {T} '(s)=\kappa (s)\mathbf {N} (s),}$

donde los primos se refieren a las derivadas con respecto a la longitud del arco s , y N ( s ) es el vector unitario normal en la dirección de T ′(s) .

Como las curvas planas tienen torsión cero , la segunda fórmula de Frenet-Serret proporciona la relación

${\displaystyle {\begin{aligned}{\frac {d\mathbf {N} }{ds}}&=-\kappa \mathbf {T} ,\\&=-\kappa {\frac {d{\boldsymbol {\gamma }}}{ds}}.\end{aligned}}}$

Para una parametrización general por un parámetro t , se necesitan expresiones que involucren derivadas con respecto a t . Como éstas se obtienen multiplicando por ⁠ds/es⁠ las derivadas con respecto a s , se tiene, para cualquier parametrización adecuada

${\displaystyle \mathbf {N} '(t)=-\kappa (t){\boldsymbol {\gamma }}'(t).}$

Peine de curvatura

Peine de curvatura

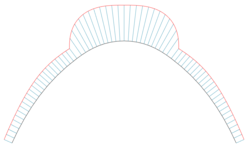
Se puede utilizar un peine de curvatura ^[8] para representar gráficamente la curvatura de cada punto de una curva. Si es una curva parametrizada, su peine se define como la curva parametrizada ${\displaystyle t\mapsto x(t)}$

${\displaystyle t\mapsto x(t)+d\kappa (t)n(t)}$

donde son el vector de curvatura y normal y es un factor de escala (que debe elegirse para mejorar la representación gráfica). ${\displaystyle \kappa ,n}$ ${\displaystyle d}$

Curvas espaciales

Animación de la curvatura y el vector de aceleración T ′( s )

Al igual que en el caso de las curvas en dos dimensiones, la curvatura de una curva espacial regular C en tres dimensiones (y superiores) es la magnitud de la aceleración de una partícula que se mueve con velocidad unitaria a lo largo de una curva. Por lo tanto, si γ ( s ) es la parametrización de la longitud de arco de C , entonces el vector tangente unitario T ( s ) viene dado por

${\displaystyle \mathbf {T} (s)={\boldsymbol {\gamma }}'(s)}$

y la curvatura es la magnitud de la aceleración:

${\displaystyle \kappa (s)=\|\mathbf {T} '(s)\|=\|{\boldsymbol {\gamma }}''(s)\|.}$

La dirección de la aceleración es el vector normal unitario N ( s ) , que se define por

${\displaystyle \mathbf {N} (s)={\frac {\mathbf {T} '(s)}{\|\mathbf {T} '(s)\|}}.}$

El plano que contiene los dos vectores T ( s ) y N ( s ) es el plano osculador de la curva en γ ( s ) . La curvatura tiene la siguiente interpretación geométrica. Existe un círculo en el plano osculador tangente a γ ( s ) cuya serie de Taylor de segundo orden en el punto de contacto concuerda con la de γ ( s ) . Este es el círculo osculador de la curva. El radio del círculo R ( s ) se llama radio de curvatura , y la curvatura es el recíproco del radio de curvatura:

${\displaystyle \kappa (s)={\frac {1}{R(s)}}.}$

La tangente, la curvatura y el vector normal describen juntos el comportamiento de segundo orden de una curva cerca de un punto. En tres dimensiones, el comportamiento de tercer orden de una curva se describe mediante una noción relacionada, la torsión , que mide el grado en que una curva tiende a moverse como una trayectoria helicoidal en el espacio. La torsión y la curvatura están relacionadas mediante las fórmulas de Frenet-Serret (en tres dimensiones) y su generalización (en dimensiones superiores).

Expresiones generales

Para una curva espacial definida paramétricamente en tres dimensiones dada en coordenadas cartesianas por γ ( t ) = ( x ( t ), y ( t ), z ( t )) , la curvatura es

${\displaystyle \kappa ={\frac {\sqrt {{\bigl (}z''y'-y''z'{\bigr )}{\vphantom {'}}^{2}+{\bigl (}x''z'-z''x'{\bigr )}{\vphantom {'}}^{2}+{\bigl (}y''x'-x''y'{\bigr )}{\vphantom {'}}^{2}}}{{\bigl (}{x'}^{2}+{y'}^{2}+{z'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},}$

donde la prima denota diferenciación respecto del parámetro t . Esto se puede expresar independientemente del sistema de coordenadas mediante la fórmula ^[9]

${\displaystyle \kappa ={\frac {{\bigl \|}{\boldsymbol {\gamma }}'\times {\boldsymbol {\gamma }}''{\bigr \|}}{{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{3}}}}$

donde × denota el producto vectorial . La siguiente fórmula es válida para la curvatura de curvas en un espacio euclidiano de cualquier dimensión:

${\displaystyle \kappa ={\frac {\sqrt {{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{2}{\bigl \|}{\boldsymbol {\gamma }}''{\bigr \|}{\vphantom {'}}^{2}-{\bigl (}{\boldsymbol {\gamma }}'\cdot {\boldsymbol {\gamma }}''{\bigr )}{\vphantom {'}}^{2}}}{{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{3}}}.}$

Curvatura a partir del arco y longitud de la cuerda

Dados dos puntos P y Q en C , sea s ( P , Q ) la longitud del arco de la porción de la curva entre P y Q y sea d ( P , Q ) la longitud del segmento de línea de P a Q. La curvatura de C en P está dada por el límite ^{[ cita requerida ]}

${\displaystyle \kappa (P)=\lim _{Q\to P}{\sqrt {\frac {24{\bigl (}s(P,Q)-d(P,Q){\bigr )}}{s(P,Q){\vphantom {Q}}^{3}}}}}$

donde el límite se toma cuando el punto Q se acerca a P en C . El denominador puede tomarse igualmente como d ( P , Q ) ³ . La fórmula es válida en cualquier dimensión. Además, al considerar el límite independientemente en cada lado de P , esta definición de la curvatura a veces puede acomodar una singularidad en P . La fórmula se verifica a continuación para el círculo osculador.

Superficies

La curvatura de las curvas dibujadas sobre una superficie es la herramienta principal para definir y estudiar la curvatura de la superficie.

Curvas en superficies

Para una curva dibujada sobre una superficie (incrustada en un espacio euclidiano tridimensional ), se definen varias curvaturas, que relacionan la dirección de la curvatura con el vector normal unitario de la superficie , incluyendo:

• curvatura normal
• curvatura geodésica
• torsión geodésica

Cualquier curva no singular sobre una superficie lisa tiene su vector tangente T contenido en el plano tangente de la superficie. La curvatura normal , k _n , es la curvatura de la curva proyectada sobre el plano que contiene la tangente T de la curva y la normal de la superficie u ; la curvatura geodésica , k _g , es la curvatura de la curva proyectada sobre el plano tangente de la superficie; y la torsión geodésica (o torsión relativa ), τ _r , mide la tasa de cambio de la normal de la superficie alrededor de la tangente de la curva.

Sea la curva parametrizada por longitud de arco y sea t = u × T de modo que T , t , u formen una base ortonormal , denominada marco de Darboux . Las cantidades anteriores están relacionadas por:

${\displaystyle {\begin{pmatrix}\mathbf {T} '\\\mathbf {t} '\\\mathbf {u} '\end{pmatrix}}={\begin{pmatrix}0&\kappa _{\mathrm {g} }&\kappa _{\mathrm {n} }\\-\kappa _{\mathrm {g} }&0&\tau _{\mathrm {r} }\\-\kappa _{\mathrm {n} }&-\tau _{\mathrm {r} }&0\end{pmatrix}}{\begin{pmatrix}\mathbf {T} \\\mathbf {t} \\\mathbf {u} \end{pmatrix}}}$

Curvatura principal

Superficie de silla de montar con planos normales en direcciones de curvaturas principales

Todas las curvas de la superficie con el mismo vector tangente en un punto dado tendrán la misma curvatura normal, que es la misma que la curvatura de la curva obtenida al intersecar la superficie con el plano que contiene a T y u . Tomando todos los vectores tangentes posibles, los valores máximo y mínimo de la curvatura normal en un punto se denominan curvaturas principales , k ₁ y k ₂ , y las direcciones de los vectores tangentes correspondientes se denominan direcciones normales principales .

Secciones normales

La curvatura se puede evaluar a lo largo de secciones normales de la superficie , de manera similar a § Curvas en superficies más arriba (ver por ejemplo el radio de curvatura de la Tierra ).

Superficies desarrollables

Algunas superficies curvas, como las que se forman a partir de una hoja de papel lisa, se pueden aplanar hasta quedar en el plano sin distorsionar sus características intrínsecas de ninguna manera. Estas superficies desarrollables tienen una curvatura gaussiana cero (véase más abajo). ^[10]

Curvatura gaussiana

A diferencia de las curvas, que no tienen curvatura intrínseca, pero sí tienen curvatura extrínseca (solo tienen una curvatura dada una incrustación), las superficies pueden tener curvatura intrínseca, independientemente de una incrustación. La curvatura gaussiana , llamada así por Carl Friedrich Gauss , es igual al producto de las curvaturas principales, k ₁ k ₂ . Tiene una dimensión de longitud ⁻² y es positiva para esferas , negativa para hiperboloides de una hoja y cero para planos y cilindros . Determina si una superficie es localmente convexa (cuando es positiva) o localmente en forma de silla de montar (cuando es negativa).

La curvatura gaussiana es una propiedad intrínseca de la superficie, lo que significa que no depende de la incrustación particular de la superficie; intuitivamente, esto significa que las hormigas que viven en la superficie podrían determinar la curvatura gaussiana. Por ejemplo, una hormiga que vive en una esfera podría medir la suma de los ángulos interiores de un triángulo y determinar que es mayor de 180 grados, lo que implica que el espacio que habita tiene una curvatura positiva. Por otro lado, una hormiga que vive en un cilindro no detectaría ninguna desviación de la geometría euclidiana ; en particular, la hormiga no podría detectar que las dos superficies tienen diferentes curvaturas medias (ver más abajo), que es un tipo de curvatura puramente extrínseca.

Formalmente, la curvatura gaussiana depende únicamente de la métrica de Riemann de la superficie. Se trata del célebre teorema egregium de Gauss , que descubrió mientras se dedicaba a los estudios geográficos y la elaboración de mapas.

Una definición intrínseca de la curvatura gaussiana en un punto P es la siguiente: imaginemos una hormiga atada a P con un hilo corto de longitud r . Corre alrededor de P mientras el hilo está completamente estirado y mide la longitud C ( r ) de una vuelta completa alrededor de P . Si la superficie fuera plana, la hormiga encontraría C ( r ) = 2π r . En superficies curvas, la fórmula para C ( r ) será diferente, y la curvatura gaussiana K en el punto P puede calcularse mediante el teorema de Bertrand–Diguet–Puiseux como

${\displaystyle K=\lim _{r\to 0^{+}}3\left({\frac {2\pi r-C(r)}{\pi r^{3}}}\right).}$

La integral de la curvatura gaussiana sobre toda la superficie está estrechamente relacionada con la característica de Euler de la superficie ; véase el teorema de Gauss-Bonnet .

El análogo discreto de la curvatura, correspondiente a la curvatura concentrada en un punto y particularmente útil para los poliedros , es el defecto (angular) ; el análogo del teorema de Gauss-Bonnet es el teorema de Descartes sobre el defecto angular total .

Dado que la curvatura (gaussiana) se puede definir sin referencia a un espacio de incrustación, no es necesario que una superficie esté incrustada en un espacio de dimensiones superiores para que sea curva. Una superficie bidimensional intrínsecamente curvada de este tipo es un ejemplo simple de una variedad de Riemann .

Curvatura media

La curvatura media es una medida extrínseca de curvatura igual a la mitad de la suma de las curvaturas principales ,k1 + k2_​​/2⁠ . Tiene una dimensión de longitud ⁻¹ . La curvatura media está estrechamente relacionada con la primera variación del área de superficie . En particular, una superficie mínima como una película de jabón tiene una curvatura media cero y una burbuja de jabón tiene una curvatura media constante. A diferencia de la curvatura de Gauss, la curvatura media es extrínseca y depende de la incrustación, por ejemplo, un cilindro y un plano son localmente isométricos pero la curvatura media de un plano es cero mientras que la de un cilindro es distinta de cero.

Segunda forma fundamental

La curvatura intrínseca y extrínseca de una superficie se puede combinar en la segunda forma fundamental. Se trata de una forma cuadrática en el plano tangente a la superficie en un punto cuyo valor en un vector tangente particular X a la superficie es el componente normal de la aceleración de una curva a lo largo de la superficie tangente a X ; es decir, es la curvatura normal a una curva tangente a X (véase más arriba). Simbólicamente,

${\displaystyle \operatorname {I\!I} (\mathbf {X} ,\mathbf {X} )=\mathbf {N} \cdot (\nabla _{\mathbf {X} }\mathbf {X} )}$

donde N es la normal unitaria a la superficie. Para los vectores tangentes unitarios X , la segunda forma fundamental supone el valor máximo k ₁ y el valor mínimo k ₂ , que se dan en las direcciones principales u ₁ y u ₂ , respectivamente. Por lo tanto, por el teorema del eje principal , la segunda forma fundamental es

${\displaystyle \operatorname {I\!I} (\mathbf {X} ,\mathbf {X} )=k_{1}\left(\mathbf {X} \cdot \mathbf {u} _{1}\right)^{2}+k_{2}\left(\mathbf {X} \cdot \mathbf {u} _{2}\right)^{2}.}$

Así, la segunda forma fundamental codifica tanto la curvatura intrínseca como la extrínseca.

Operador de forma

Una encapsulación de la curvatura de la superficie se puede encontrar en el operador de forma, S , que es un operador lineal autoadjunto del plano tangente a sí mismo (específicamente, la diferencial del mapa de Gauss ).

Para una superficie con vectores tangentes X y normal N , el operador de forma se puede expresar de forma compacta en notación de suma de índices como

${\displaystyle \partial _{a}\mathbf {N} =-S_{ba}\mathbf {X} _{b}.}$

(Compare la expresión alternativa de curvatura para una curva plana).

Las ecuaciones de Weingarten dan el valor de S en términos de los coeficientes de la primera y segunda formas fundamentales como

${\displaystyle S=\left(EG-F^{2}\right)^{-1}{\begin{pmatrix}eG-fF&fG-gF\\fE-eF&gE-fF\end{pmatrix}}.}$

Las curvaturas principales son los valores propios del operador de forma, las direcciones de curvatura principal son sus vectores propios , la curvatura de Gauss es su determinante y la curvatura media es la mitad de su traza .

Curvatura del espacio

Por extensión del argumento anterior, un espacio de tres o más dimensiones puede ser intrínsecamente curvo. La curvatura es intrínseca en el sentido de que es una propiedad definida en cada punto del espacio, en lugar de una propiedad definida con respecto a un espacio más grande que lo contiene. En general, un espacio curvo puede o no concebirse como integrado en un espacio circundante de dimensiones superiores ; de lo contrario, su curvatura solo puede definirse intrínsecamente.

Tras el descubrimiento de la definición intrínseca de curvatura, que está estrechamente relacionada con la geometría no euclidiana , muchos matemáticos y científicos cuestionaron si el espacio físico ordinario podía ser curvo, aunque el éxito de la geometría euclidiana hasta ese momento significaba que el radio de curvatura debía ser astronómicamente grande. En la teoría de la relatividad general , que describe la gravedad y la cosmología , la idea se generaliza ligeramente a la "curvatura del espacio-tiempo "; en la teoría de la relatividad, el espacio-tiempo es una variedad pseudo-riemanniana . Una vez que se define una coordenada temporal, el espacio tridimensional correspondiente a un tiempo particular es generalmente una variedad riemanniana curva; pero dado que la elección de la coordenada temporal es en gran medida arbitraria, es la curvatura subyacente del espacio-tiempo la que es físicamente significativa.

Aunque un espacio de curvatura arbitraria es muy complejo de describir, la curvatura de un espacio que es localmente isótropo y homogéneo se describe mediante una única curvatura gaussiana, como para una superficie; matemáticamente, estas son condiciones fuertes, pero corresponden a supuestos físicos razonables (todos los puntos y todas las direcciones son indistinguibles). Una curvatura positiva corresponde al radio de curvatura del cuadrado inverso; un ejemplo es una esfera o hiperesfera . Un ejemplo de espacio de curvatura negativa es la geometría hiperbólica (ver también: curvatura no positiva ). Un espacio o espacio-tiempo con curvatura cero se llama plano .Por ejemplo, el espacio euclidiano es un ejemplo de espacio plano, y el espacio de Minkowski es un ejemplo de espacio-tiempo plano. Sin embargo, existen otros ejemplos de geometrías planas en ambos contextos. Tanto a un toro como a un cilindro se les pueden dar métricas planas, pero difieren en su topología . También son posibles otras topologías para el espacio curvo (véase también: Forma del universo ) .

Generalizaciones

Al mover un vector a lo largo de una curva desde A → N → B → A se produce otro vector. La imposibilidad de volver al vector inicial se mide por la holonomía de la superficie. En un espacio sin curvatura, el ángulo α es de 0 grados, y en un espacio con curvatura, el ángulo α es mayor que 0 grados. Cuanto más curvado esté el espacio, mayor será la magnitud del ángulo α.

La noción matemática de curvatura también se define en contextos mucho más generales. ^[11] Muchas de estas generalizaciones enfatizan diferentes aspectos de la curvatura tal como se entiende en dimensiones inferiores.

Una de esas generalizaciones es la cinemática. La curvatura de una curva puede considerarse naturalmente como una cantidad cinemática, que representa la fuerza que siente un determinado observador al moverse a lo largo de la curva; de manera análoga, la curvatura en dimensiones superiores puede considerarse como una especie de fuerza de marea (esta es una forma de pensar en la curvatura seccional ). Esta generalización de la curvatura depende de cómo divergen o convergen las partículas de prueba cercanas cuando se les permite moverse libremente en el espacio; véase el campo de Jacobi .

Otra amplia generalización de la curvatura proviene del estudio del transporte paralelo en una superficie. Por ejemplo, si un vector se mueve alrededor de un bucle en la superficie de una esfera manteniéndose paralelo durante todo el movimiento, entonces la posición final del vector puede no ser la misma que la posición inicial del vector. Este fenómeno se conoce como holonomía . ^[12] Varias generalizaciones capturan en una forma abstracta esta idea de curvatura como una medida de holonomía; vea forma de curvatura . Una noción estrechamente relacionada de curvatura proviene de la teoría de calibre en física, donde la curvatura representa un campo y un potencial vectorial para el campo es una cantidad que en general depende de la trayectoria: puede cambiar si un observador se mueve alrededor de un bucle.

Dos generalizaciones más de la curvatura son la curvatura escalar y la curvatura de Ricci . En una superficie curva como la esfera, el área de un disco en la superficie difiere del área de un disco del mismo radio en el espacio plano. Esta diferencia (en un límite adecuado) se mide mediante la curvatura escalar. La diferencia en el área de un sector del disco se mide mediante la curvatura de Ricci. Tanto la curvatura escalar como la curvatura de Ricci se definen de forma análoga en tres dimensiones y en dimensiones superiores. Son particularmente importantes en la teoría de la relatividad, donde ambas aparecen en el lado de las ecuaciones de campo de Einstein que representan la geometría del espacio-tiempo (el otro lado representa la presencia de materia y energía). Estas generalizaciones de la curvatura subyacen, por ejemplo, en la noción de que la curvatura puede ser una propiedad de una medida ; véase curvatura de una medida .

Otra generalización de la curvatura se basa en la capacidad de comparar un espacio curvo con otro espacio que tiene una curvatura constante . A menudo, esto se hace con triángulos en los espacios. La noción de triángulo tiene sentido en los espacios métricos , y esto da lugar a los espacios CAT( k ) .

Véase también

• Forma de curvatura para la noción apropiada de curvatura para fibrados vectoriales y fibrados principales con conexión
• Curvatura de una medida para una noción de curvatura en la teoría de la medida
• Curvatura de superficies paramétricas
• Curvatura de variedades de Riemann para generalizaciones de la curvatura de Gauss a variedades de Riemann de dimensiones superiores
• Vector de curvatura y curvatura geodésica para nociones apropiadas de curvatura de curvas en variedades de Riemann, de cualquier dimensión
• Grado de curvatura
• Geometría diferencial de curvas para un tratamiento completo de curvas insertas en un espacio euclidiano de dimensión arbitraria
• Dioptría , una medida de curvatura utilizada en óptica.
• Evoluta , el lugar geométrico de los centros de curvatura de una curva dada
• Teorema fundamental de las curvas
• Teorema de Gauss-Bonnet para una aplicación elemental de la curvatura
• Mapa de Gauss para más propiedades geométricas de la curvatura de Gauss
• Principio de mínima restricción de Gauss , una expresión del principio de mínima acción
• Curvatura media en un punto de una superficie
• Radio mínimo de curva de ferrocarril
• Radio de curvatura
• Segunda forma fundamental de la curvatura extrínseca de las hipersuperficies en general
• Sinuosidad
• Torsión de una curva

Notas

1. Clagett, Marshall (1968), Nicole Oresme y la geometría medieval de cualidades y movimientos; un tratado sobre la uniformidad y disformidad de las intensidades conocido como Tractatus de configurationibus qualitatum et motuum, Madison, WI: Prensa de la Universidad de Wisconsin, ISBN 0-299-04880-2
2. Serrano, Isabel; Suceavă, Bogdan (2015). "Un misterio medieval: el concepto de curvitas de Nicole Oresme" (PDF) . Avisos de la American Mathematical Society . 62 (9): 1030–1034. doi : 10.1090/noti1275 .
3. Borovik, Alexandre ; Katz, Mikhail G. (2011), "¿Quién te dio el cuento de Cauchy-Weierstrass? La historia dual del cálculo riguroso", Foundations of Science , 17 (3): 245–276, arXiv : 1108.2885 , Bibcode :2011arXiv1108.2885B, doi :10.1007/s10699-011-9235-x, S2CID  119320059
4. Pressley, Andrew (14 de junio de 2010). Geometría diferencial elemental (1.ª ed.). Cambridge University Press . pág. 29. ISBN 978-0521896719.
5. Kline, Morris (1998). Cálculo: un enfoque intuitivo y físico (2.ª ed.). Dover Publications. pág. 458. ISBN 0486404536. Número de LCCN  98036211.
6. Kennedy, John (2011). "La parametrización de la longitud de arco de una curva". Archivado desde el original el 28 de septiembre de 2015. Consultado el 10 de diciembre de 2013 .
7. Goldman, Ron (2005). "Fórmulas de curvatura para curvas y superficies implícitas". Diseño geométrico asistido por ordenador . 22 (7): 632–658. CiteSeerX 10.1.1.413.3008 . doi :10.1016/j.cagd.2005.06.005. 
8. Farin, Gerald (2016). "Peines de curvatura y gráficos de curvatura". Diseño asistido por ordenador . 80 : 6–8. doi :10.1016/j.cad.2016.08.003.
9. Una prueba de esto se puede encontrar en el artículo sobre curvatura en Wolfram MathWorld .
10. superficie desarrollable, Mathworld. (Consultado el 11 de febrero de 2021)
11. Kobayashi, Shoshichi ; Nomizu, Katsumi (1963). Fundamentos de geometría diferencial (1.ª ed.). Wiley Interscience . vol. 1 cap. 2–3. ISBN 9780470496473.
12. Henderson, David W. ; Taimiņa, Daina (23 de julio de 2019). Experimentando la geometría (3.ª ed.). Pearson . págs. 98–99. ISBN 978-0131437487.

Referencias

• Coolidge, Julian L. (junio de 1952). "La historia insatisfactoria de la curvatura". American Mathematical Monthly . 59 (6): 375–379. doi :10.2307/2306807. JSTOR  2306807.
• Sokolov, Dmitriĭ Dmitrievich (2001) [1994], "Curvatura", Enciclopedia de Matemáticas , EMS Press
• Kline, Morris (1998). Cálculo: un enfoque intuitivo y físico . Dover. pp. 457–461. ISBN 978-0-486-40453-0.( copia restringida en línea , p. 457, en Google Books )
• Klaf, A. Albert (1956). Actualización de cálculo . Dover. Págs. 151–168. ISBN. 978-0-486-20370-6.( copia restringida en línea , p. 151, en Google Books )
• Casey, James (1996). Explorando la curvatura . Vieweg+Teubner. ISBN 978-3-528-06475-4.

Enlaces externos

• Las conferencias de física de Feynman, vol. II, cap. 42: El espacio curvo
• La historia de la curvatura
• Curvatura intrínseca y extrínseca en MathPages