En geometría , un politopo uniforme de 4 (o policorón uniforme ) [1] es un politopo de 4 dimensiones que es transitivo por vértices y cuyas celdas son poliedros uniformes y las caras son polígonos regulares .
Hay 47 4 politopos uniformes convexos no prismáticos . Hay dos conjuntos infinitos de formas prismáticas convexas, junto con 17 casos que surgen como prismas de poliedros uniformes convexos. También hay un número desconocido de formas estelares no convexas.
Los 4 politopos regulares son un subconjunto de los 4 politopos uniformes, que satisfacen requisitos adicionales. Los 4 politopos regulares se pueden expresar con el símbolo de Schläfli { p , q , r } y tienen celdas de tipo { p , q }, caras de tipo { p }, figuras de aristas { r } y figuras de vértices { q , r }.
La existencia de un politopo regular de 4 { p , q , r } está limitada por la existencia de los poliedros regulares { p , q } que se convierten en celdas y { q , r } que se convierte en la figura de vértice .
La existencia como un politopo finito de 4 depende de una desigualdad: [15]
Los 16 4 politopos regulares , con la propiedad de que todas las celdas, caras, aristas y vértices son congruentes:
Hay 5 familias de grupos de puntos de simetría especular fundamentales en 4 dimensiones: A 4 =
, B 4 =
, re 4 =
, F 4 =, H 4 =
. [7] También hay 3 grupos prismáticos A 3 A 1 =
, B 3 A 1 =, H 3 A 1 =, y grupos duoprismáticos: I 2 (p)×I 2 (q) =
. Cada grupo definido por un dominio fundamental de tetraedro Goursat delimitado por planos especulares.
Cada 4 politopo reflectante uniforme se puede construir en uno o más grupos de puntos reflectantes en 4 dimensiones mediante una construcción de Wythoff , representada por anillos alrededor de permutaciones de nodos en un diagrama de Coxeter . Los hiperplanos espejo se pueden agrupar, como se ve mediante nodos coloreados, separados por ramas pares. Los grupos de simetría de la forma [a,b,a], tienen una simetría extendida, [[a,b,a]], duplicando el orden de simetría. Esto incluye [3,3,3], [3,4,3] y [ p ,2, p ]. Los politopos uniformes en este grupo con anillos simétricos contienen esta simetría extendida.
Si todos los espejos de un color determinado no tienen anillos (inactivos) en un politopo uniforme determinado, tendrá una construcción de simetría más baja al eliminar todos los espejos inactivos. Si todos los nodos de un color determinado están anillados (activos), una operación de alternancia puede generar un nuevo politopo de 4 con simetría quiral, que se muestra como "nodos circulares" vacíos ", pero la geometría generalmente no es ajustable para crear soluciones uniformes.
Hay 64 4 politopos uniformes convexos, incluidos los 6 4 politopos convexos regulares y excluyendo los conjuntos infinitos de los duoprismas y los prismas antiprismáticos .
Estos 64 4 politopos uniformes están indexados a continuación por George Olshevsky. Las formas de simetría repetidas están indexadas entre paréntesis.
Además de los 64 anteriores, hay 2 conjuntos prismáticos infinitos que generan todas las formas convexas restantes:
Las 5 celdas tienen simetría pentacórica diploide [3,3,3] , [7] de orden 120, isomorfa a las permutaciones de cinco elementos, porque todos los pares de vértices están relacionados de la misma manera.
Se proporcionan facetas (celdas), agrupadas en sus ubicaciones del diagrama de Coxeter eliminando nodos específicos.
Las tres formas uniformes de 4 politopos marcadas con un asterisco , * , tienen la simetría pentacórica extendida más alta , de orden 240, [[3,3,3]] porque el elemento correspondiente a cualquier elemento de las 5 celdas subyacentes se puede intercambiar. con uno de los correspondientes a un elemento de su dual. Hay un pequeño subgrupo de índice [3,3,3] + , orden 60, o su duplicación [[3,3,3]] + , orden 120, que define un omnisnub de 5 celdas que se enumera para completar, pero no uniforme.
Esta familia tiene simetría hexadecacórica diploide , [7] [4,3,3], de orden 24×16=384: 4!=24 permutaciones de los cuatro ejes, 2 4 =16 para reflexión en cada eje. Hay 3 pequeños subgrupos de índices, y los dos primeros generan 4 politopos uniformes que también se repiten en otras familias, [1 + , 4,3,3], [4,(3,3) + ] y [4, 3,3] + , todo orden 192.
El desaire de 24 celdas se repite en esta familia para que esté completo. Es una alternancia del grupo cantitruncado de 16 celdas o truncado de 24 celdas , con el grupo de semisimetría [(3,3) + ,4]. Las células octaédricas truncadas se convierten en icosaedros. Los cubos se convierten en tetraedros y se crean 96 nuevos tetraedros en los espacios de los vértices eliminados.
Esta familia tiene simetría icositetracórica diploide , [7] [3,4,3], de orden 24×48=1152: las 48 simetrías del octaedro para cada una de las 24 celdas. Hay 3 pequeños subgrupos de índices, y los dos primeros pares isomórficos generan 4 politopos uniformes que también se repiten en otras familias, [3 + , 4,3], [3,4,3 + ] y [3,4, 3] + , todo orden 576.
Al igual que el de 5 celdas, el de 24 celdas es autodual, por lo que las siguientes tres formas tienen el doble de simetrías, lo que eleva su total a 2304 ( simetría icositetracórica extendida [[3,4,3]]).
Esta familia tiene simetría hexacosicórica diploide , [7] [5,3,3], de orden 120×120=24×600=14400: 120 para cada uno de los 120 dodecaedros, o 24 para cada uno de los 600 tetraedros. Hay un pequeño subgrupo de índice [5,3,3] + , todos del orden 7200.
Esta familia demitesseract , [3 1,1,1 ], no introduce nuevos 4 politopos uniformes, pero vale la pena repetir estas construcciones alternativas. Esta familia tiene orden 12×16=192: 4!/2=12 permutaciones de los cuatro ejes, la mitad alternados, 2 4 =16 para reflexión en cada eje. Hay un pequeño subgrupo de índice que genera 4 politopos uniformes, [3 1,1,1 ] + , orden 96.
Cuando los 3 nodos de las ramas bifurcadas tienen anillos idénticos, la simetría se puede aumentar en 6, como [3[3 1,1,1 ]] = [3,4,3] y, por lo tanto, estos politopos se repiten desde las 24 celdas. familia.
Aquí nuevamente el desaire de 24 celdas , con el grupo de simetría [3 1,1,1 ] + esta vez, representa un truncamiento alternado de las 24 celdas truncadas creando 96 nuevos tetraedros en la posición de los vértices eliminados. En contraste con su aparición dentro de los grupos anteriores como 4 politopo parcialmente desairado, sólo dentro de este grupo de simetría tiene la analogía completa con los desaires de Kepler, es decir, el cubo desaire y el dodecaedro desaire .
Hay un 4 politopo convexo uniforme no wythoffiano, conocido como gran antiprisma , que consta de 20 antiprismas pentagonales que forman dos anillos perpendiculares unidos por 300 tetraedros . Es vagamente análogo a los antiprismas tridimensionales , que constan de dos polígonos paralelos unidos por una banda de triángulos . A diferencia de ellos, sin embargo, el gran antiprisma no es miembro de una familia infinita de politopos uniformes.
Su simetría es el grupo iónico de Coxeter disminuido , [[10,2 + ,10]], orden 400.
Un politopo prismático es un producto cartesiano de dos politopos de dimensión inferior; ejemplos familiares son los prismas tridimensionales , que son productos de un polígono y un segmento de recta . Los 4 politopos prismáticos uniformes constan de dos familias infinitas:
La familia más obvia de 4 politopos prismáticos son los prismas poliédricos, es decir, productos de un poliedro con un segmento de recta . Las células de estos 4 politopos son dos poliedros uniformes idénticos que se encuentran en hiperplanos paralelos (las células base ) y una capa de prismas que los une (las células laterales ). Esta familia incluye prismas para los 75 poliedros uniformes no prismáticos (de los cuales 18 son convexos; uno de ellos, el cubo-prisma, figura arriba como teseracto ). [ cita necesaria ]
Hay 18 prismas poliédricos convexos creados a partir de 5 sólidos platónicos y 13 sólidos de Arquímedes , así como de las infinitas familias de prismas y antiprismas tridimensionales . [ cita necesaria ] El número de simetría de un prisma poliédrico es el doble que el del poliedro base.
Esta simetría tetraédrica prismática es [3,3,2], orden 48. Hay dos subgrupos de índice 2, [(3,3) + ,2] y [3,3,2] + , pero el segundo no genera un 4 politopo uniforme.
Esta simetría familiar prismática octaédrica es [4,3,2], orden 96. Hay 6 subgrupos de índice 2, orden 48 que se expresan en 4 politopos alternados a continuación. Las simetrías son [(4,3) + ,2], [1 + ,4,3,2], [4,3,2 + ], [4,3 + ,2], [4,(3,2) + ] y [4,3,2] + .
Esta simetría prismática icosaédrica es [5,3,2], orden 240. Hay dos subgrupos de índice 2, [(5,3) + ,2] y [5,3,2] + , pero el segundo no genera un policorón uniforme.
La segunda es la familia infinita de duoprismas uniformes , productos de dos polígonos regulares . El diagrama de Coxeter-Dynkin de un duoprisma es
. Su figura de vértice es un tetraedro disfenoide ,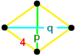
.
Esta familia se superpone con la primera: cuando uno de los dos polígonos "factoriales" es un cuadrado, el producto equivale a un hiperprisma cuya base es un prisma tridimensional. El número de simetría de un duoprisma cuyos factores son un p -gon y un q -gon (un " p,q -duoprisma") es 4 pq si p ≠ q ; si ambos factores son p -gons, el número de simetría es 8 p 2 . El teseracto también puede considerarse un 4,4-duoprisma.
El vector f extendido de { p }×{ q } es ( p , p ,1)*( q , q ,1) = ( pq ,2 pq , pq + p + q , p + q ).
No existe un análogo uniforme en cuatro dimensiones para la familia infinita de antiprismas tridimensionales .
Conjunto infinito de duoprisma pq -- p q -prismas gonales, q p -prismas gonales:
Las alternancias son posibles.
=da la familia de duoantiprismas , pero generalmente no pueden uniformarse. p=q=2 es el único caso convexo que se puede uniformar, dando las 16 celdas regulares. p=5, q=5/3 es el único caso no convexo que puede uniformarse, dando el llamado gran duoantiprisma .da el prismantiprismoide p-2q-gonal (una alternancia de bordes del duoprisma 2p-4q), pero esto no puede uniformarse en ningún caso. [20]
El conjunto infinito de prismas prismáticos uniformes se superpone con los duoprismas de 4 p: (p≥3) -- p cubos y 4 p prismas -gonales - (Todos son iguales que el duoprisma 4-p ) El segundo politopo de la serie es una simetría inferior del teseracto regular , {4}×{4}.
Los infinitos conjuntos de prismas antiprismáticos uniformes se construyen a partir de dos antiprismas uniformes paralelos ): (p≥2) -- 2 antiprismas p -gonales, conectados por 2 prismas p -gonales y 2p prismas triangulares.
Un prisma antiprismático p-gonal tiene 4p triángulos, 4p cuadrados y 4 p-gonos. Tiene aristas de 10p y vértices de 4p .
, una alternancia elimina la mitad de los vértices, en dos conjuntos quirales de vértices de la forma anillada, sin embargo, la solución uniforme requiere que las posiciones de los vértices se ajusten para longitudes iguales. En cuatro dimensiones, este ajuste sólo es posible para 2 figuras alternadas, mientras que el resto sólo existen como figuras alternadas no equiláteras.Coxeter mostró solo dos soluciones uniformes para grupos de Coxeter de rango 4 con todos los anillos alternados (se muestran con nodos circulares vacíos). El primero es, s{2 1,1,1 } que representaba una forma de subgrupo de índice 24 ( simetría [2,2,2] + , orden 8) del demitesseract ,, h{4,3,3} (simetría [1 + ,4,3,3] = [3 1,1,1 ], orden 192). El segundo es
, s{3 1,1,1 }, que es una forma de subgrupo de índice 6 (simetría [3 1,1,1 ] + , orden 96) de la forma chata de 24 celdas ,, s{3,4,3}, (simetría [3 + ,4,3], orden 576).
Otras alternancias, como, como una alternancia del tesseract omnitruncado , no se puede hacer uniforme ya que la resolución de longitudes de aristas iguales está en general sobredeterminada (hay seis ecuaciones pero solo cuatro variables). Estas figuras alternadas no uniformes se pueden construir como 4 politopos transitivos por vértices mediante la eliminación de uno de los dos medios conjuntos de vértices de la figura anillada completa, pero tendrán longitudes de bordes desiguales. Al igual que las alternancias uniformes, tendrán la mitad de la simetría de la figura uniforme, como [4,3,3] + , orden 192, es la simetría del teseracto omnitruncado alternado . [21]
Las construcciones de Wythoff con alternancias producen figuras transitivas de vértices que pueden hacerse equiláteras, pero no uniformes porque los espacios alternos (alrededor de los vértices eliminados) crean celdas que no son regulares ni semirregulares. Un nombre propuesto para tales figuras es politopos escaliformes . [22] Esta categoría permite un subconjunto de sólidos de Johnson como celdas, por ejemplo una cúpula triangular .
Cada configuración de vértice dentro de un sólido de Johnson debe existir dentro de la figura de vértice. Por ejemplo, una pirámide cuadrada tiene dos configuraciones de vértices: 3.3.4 alrededor de la base y 3.3.3.3 en el vértice.
A continuación se muestran las redes y las figuras de los vértices de los cuatro casos equiláteros convexos, junto con una lista de celdas alrededor de cada vértice.
Los 46 4 politopos wythoffianos incluyen los seis 4 politopos regulares convexos . Los otros cuarenta pueden derivarse de la policora regular mediante operaciones geométricas que conservan la mayoría o la totalidad de sus simetrías y, por tanto, pueden clasificarse por los grupos de simetría que tienen en común.
Las operaciones geométricas que derivan los 40 4 politopos uniformes de los 4 politopos regulares son operaciones de truncamiento . Un politopo de 4 puede truncarse en los vértices, aristas o caras, lo que lleva a la adición de celdas correspondientes a esos elementos, como se muestra en las columnas de las tablas siguientes.
El diagrama de Coxeter-Dynkin muestra los cuatro espejos del caleidoscopio wythoffiano como nodos, y los bordes entre los nodos están etiquetados por un número entero que muestra el ángulo entre los espejos ( π / n radianes o 180/ n grados). Los nodos circulares muestran qué espejos están activos para cada formulario; un espejo está activo con respecto a un vértice que no se encuentra sobre él.
Véase también panales uniformes convexos , algunos de los cuales ilustran estas operaciones aplicadas al panal cúbico regular .
Si dos politopos son duales entre sí (como el tesseract y el de 16 celdas, o el de 120 celdas y el de 600 celdas), entonces el bitruncating , el runcinating o el omnitruncating producen la misma figura que la misma operación para el otro. Por lo tanto, cuando en la tabla sólo aparece el participio, debe entenderse que se aplica a cualquiera de los padres.
Las 46 policoras uniformes construidas a partir de la simetría A 4 , B 4 , F 4 , H 4 se dan en esta tabla mediante su simetría extendida completa y diagramas de Coxeter. También se incluye la simetría D 4 , aunque sólo crea duplicados. Las alternancias se agrupan por su simetría quiral. Se dan todas las alternancias, aunque el chato de 24 celdas , con sus 3 construcciones de diferentes familias es el único que resulta uniforme. Los conteos entre paréntesis son repetidos o no uniformes. Los diagramas de Coxeter se dan con índices de subíndices del 1 al 46. Se incluye la familia duoprismática 3-3 y 4-4, la segunda por su relación con la familia B 4 .
Además de las familias de prismas de duoprisma y antiprisma infinitos antes mencionadas, que tienen una cantidad infinita de miembros no convexos, se han descubierto muchas policoras estelares uniformes. En 1852, Ludwig Schläfli descubrió cuatro policoras de estrellas regulares : {5,3,5/2}, {5/2,3,5}, {3,3,5/2} y {5/2,3,3 }. En 1883, Edmund Hess encontró los otros seis: {3,5,5/2}, {5/2,5,3}, {5,5/2,5}, {5/2,5,5/2 }, {5,5/2,3} y {3,5/2,5}. Norman Johnson describió tres policoras estelares uniformes similares a antiprismas en su tesis doctoral de 1966: se basan en los tres poliedros ditrigonales que comparten los bordes y vértices del dodecaedro regular. Desde entonces, otros investigadores, incluidos Jonathan Bowers y George Olshevsky, han encontrado muchos más, creando un recuento total de 2127 policoras estelares uniformes conocidas en la actualidad (sin contar el conjunto infinito de duoprismas basados en polígonos estelares). Actualmente no hay pruebas de que el conjunto esté completo.
{{cite web}}: Mantenimiento CS1: copia archivada como título ( enlace )