Límite (teoría de categorías)

Concepto matemático

En la teoría de categorías , una rama de las matemáticas , la noción abstracta de límite captura las propiedades esenciales de construcciones universales como productos , pullbacks y límites inversos . La noción dual de colimite generaliza construcciones como uniones disjuntas , sumas directas , coproductos , pushouts y límites directos .

Los límites y colímites, al igual que las nociones estrechamente relacionadas de propiedades universales y funtores adjuntos , existen en un alto nivel de abstracción. Para comprenderlos, es útil estudiar primero los ejemplos específicos que estos conceptos pretenden generalizar.

Definición

Los límites y colímites de una categoría se definen mediante diagramas en . Formalmente, un diagrama de forma en es un funtor de a : ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle J}$ ${\displaystyle C}$ ${\displaystyle J}$ ${\displaystyle C}$

${\displaystyle F:J\to C.}$

La categoría se considera como una categoría de índice , y el diagrama se considera como la indexación de una colección de objetos y morfismos en patrones . ${\displaystyle J}$ ${\displaystyle F}$ ${\displaystyle C}$ ${\displaystyle J}$

Lo más frecuente es que nos interese el caso en que la categoría sea pequeña o incluso finita . Se dice que un diagrama es pequeño o finito siempre que sea. ${\displaystyle J}$ ${\displaystyle J}$

Límites

Sea un diagrama de forma en una categoría . Un cono a es un objeto de junto con una familia de morfismos indexados por los objetos de , de modo que para cada morfismo en , tenemos . ${\displaystyle F:J\to C}$ ${\displaystyle J}$ ${\displaystyle C}$ ${\displaystyle F}$ ${\displaystyle N}$ ${\displaystyle C}$ ${\displaystyle \psi _{X}:N\to F(X)}$ ${\displaystyle X}$ ${\displaystyle J}$ ${\displaystyle f:X\to Y}$ ${\displaystyle J}$ ${\displaystyle F(f)\circ \psi _{X}=\psi _{Y}}$

Un límite del diagrama es un cono a tal que para cada cono a existe un morfismo único tal que para todo en . ${\displaystyle F:J\to C}$ ${\displaystyle (L,\phi )}$ ${\displaystyle F}$ ${\displaystyle (N,\psi )}$ ${\displaystyle F}$ ${\displaystyle u:N\to L}$ ${\displaystyle \phi _{X}\circ u=\psi _{X}}$ ${\displaystyle X}$ ${\displaystyle J}$

Un cono universal

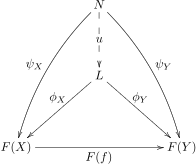
Se dice que el cono se factoriza a través del cono con la factorización única . El morfismo a veces se denomina morfismo mediador . ${\displaystyle (N,\psi )}$ ${\displaystyle (L,\phi )}$ ${\displaystyle u}$ ${\displaystyle u}$

Los límites también se denominan conos universales , ya que se caracterizan por una propiedad universal (consulte a continuación para obtener más información). Como ocurre con todas las propiedades universales, la definición anterior describe un estado equilibrado de generalidad: el objeto límite debe ser lo suficientemente general como para permitir que cualquier cono se factorice a través de él; por otro lado, debe ser lo suficientemente específico, de modo que solo sea posible una factorización de este tipo para cada cono. ${\displaystyle L}$ ${\displaystyle L}$

Los límites también pueden caracterizarse como objetos terminales en la categoría de conos a F .

Es posible que un diagrama no tenga ningún límite. Sin embargo, si un diagrama tiene un límite, este es esencialmente único: es único hasta un isomorfismo único . Por esta razón, a menudo se habla del límite de F.

Colimites

Las nociones duales de límites y conos son colimites y coconos. Aunque es fácil obtener sus definiciones invirtiendo todos los morfismos de las definiciones anteriores, las enunciaremos explícitamente aquí:

Un cocono de un diagrama es un objeto junto con una familia de morfismos. ${\displaystyle F:J\to C}$ ${\displaystyle N}$ ${\displaystyle C}$

${\displaystyle \psi _{X}:F(X)\to N}$

para cada objeto de , tal que para cada morfismo en , tenemos . ${\displaystyle X}$ ${\displaystyle J}$ ${\displaystyle f:X\to Y}$ ${\displaystyle J}$ ${\displaystyle \psi _{Y}\circ F(f)=\psi _{X}}$

Un colimite de un diagrama es un cocono de tal que para cualquier otro cocono de existe un morfismo único tal que para todo en . ${\displaystyle F:J\to C}$ ${\displaystyle (L,\phi )}$ ${\displaystyle F}$ ${\displaystyle (N,\psi )}$ ${\displaystyle F}$ ${\displaystyle u:L\to N}$ ${\displaystyle u\circ \phi _{X}=\psi _{X}}$ ${\displaystyle X}$ ${\displaystyle J}$

Un coco universal

Los colimits también se denominan coconos universales y pueden caracterizarse como objetos iniciales en la categoría de coconos de . ${\displaystyle F}$

Al igual que con los límites, si un diagrama tiene un colimite, entonces este colimite es único hasta un isomorfismo único. ${\displaystyle F}$

Variaciones

También se pueden definir límites y colímites para colecciones de objetos y morfismos sin el uso de diagramas. Las definiciones son las mismas (nótese que en las definiciones anteriores nunca necesitamos usar la composición de morfismos en ). Sin embargo, esta variación no agrega información nueva. Cualquier colección de objetos y morfismos define un grafo dirigido (posiblemente grande) . Si dejamos que sea la categoría libre generada por , hay un diagrama universal cuya imagen contiene . El límite (o colímite) de este diagrama es el mismo que el límite (o colímite) de la colección original de objetos y morfismos. ${\displaystyle J}$ ${\displaystyle G}$ ${\displaystyle J}$ ${\displaystyle G}$ ${\displaystyle F:J\to C}$ ${\displaystyle G}$

El límite débil y los colímites débiles se definen como límites y colímites, excepto que se descarta la propiedad de unicidad del morfismo mediador.

Ejemplos

Límites

La definición de límites es lo suficientemente general como para abarcar varias construcciones útiles en la práctica. A continuación, consideraremos el límite ( L , φ ) de un diagrama F  : J → C .

• Objetos terminales . Si J es la categoría vacía, solo hay un diagrama de forma J : el vacío (similar a la función vacía en la teoría de conjuntos). Un cono del diagrama vacío es esencialmente solo un objeto de C. El límite de F es cualquier objeto que sea factorizado de manera única por todos los demás objetos. Esta es solo la definición de un objeto terminal .
• Productos . Si J es una categoría discreta , entonces un diagrama F no es esencialmente nada más que una familia de objetos de C , indexados por J. El límite L de F se llama producto de estos objetos. El cono φ consiste en una familia de morfismos φ _X  : L → F ( X ) llamados proyecciones del producto. En la categoría de conjuntos , por ejemplo, los productos están dados por productos cartesianos y las proyecciones son simplemente las proyecciones naturales sobre los diversos factores.
  • Potencias . Un caso especial de un producto es cuando el diagrama F es un funtor constante ^de un objeto X de C. El límite de este diagrama se llama potencia J de X y se denota X ^J.
• Ecualizadores . Si J es una categoría con dos objetos y dos morfismos paralelos de un objeto al otro, entonces un diagrama de forma J es un par de morfismos paralelos en C. El límite L de un diagrama de este tipo se denomina ecualizador de esos morfismos.
  • Núcleos . Un núcleo es un caso especial de ecualizador donde uno de los morfismos es un morfismo cero .
• Retrocesos . Sea F un diagrama que selecciona tres objetos X , Y y Z en C , donde los únicos morfismos no idénticos son f  : X → Z y g  : Y → Z. El límite L de F se denomina retroceso o producto de fibra . Se puede visualizar bien como un cuadrado conmutativo :

• Límites inversos . Sea J un conjunto dirigido (considerado como una pequeña categoría añadiendo flechas i → j si y solo si i ≥ j ) y sea F  : J ^op → C un diagrama. El límite de F se llama límite inverso o límite proyectivo .
• Si J = 1 , la categoría con un único objeto y morfismo, entonces un diagrama de forma J es esencialmente sólo un objeto X de C . Un cono a un objeto X es sólo un morfismo con codominio X . Un morfismo f  : Y → X es un límite del diagrama X si y sólo si f es un isomorfismo . De forma más general, si J es cualquier categoría con un objeto inicial i , entonces cualquier diagrama de forma J tiene un límite, es decir, cualquier objeto isomorfo a F ( i ). Tal isomorfismo determina de forma única un cono universal a F .
• Límites topológicos . Los límites de funciones son un caso especial de límites de filtros , que se relacionan con los límites categóricos de la siguiente manera. Dado un espacio topológico X , denotemos por F el conjunto de filtros en X , x ∈ X un punto, V ( x ) ∈ F el filtro de vecindad de x , A ∈ F un filtro particular y el conjunto de filtros más finos que A y que convergen a x . A los filtros F se les da una estructura de categoría pequeña y delgada agregando una flecha A → B si y solo si A ⊆ B. La inyección se convierte en un funtor y se cumple la siguiente equivalencia: ${\displaystyle F_{x,A}=\{G\in F\mid V(x)\cup A\subset G\}}$ ${\displaystyle I_{x,A}:F_{x,A}\to F}$

x es un límite topológico de A si y sólo si A es un límite categórico de ${\displaystyle I_{x,A}}$

Colimites

Ejemplos de colimites se dan mediante las versiones duales de los ejemplos anteriores:

• Los objetos iniciales son colimites de diagramas vacíos.
• Los coproductos son colímites de diagramas indexados por categorías discretas.
  • Las copotencias son colimites de diagramas constantes de categorías discretas.
• Los coecualizadores son colímites de un par paralelo de morfismos.
  • Los cokernels son coecualizadores de un morfismo y un morfismo cero paralelo.
• Los pushouts son colimites de un par de morfismos con dominio común.
• Los límites directos son colimites de diagramas indexados por conjuntos dirigidos.

Propiedades

Existencia de límites

Un diagrama dado F  : J → C puede tener o no un límite (o colimite) en C . De hecho, puede que ni siquiera exista un cono en F , y mucho menos un cono universal.

Se dice que una categoría C tiene límites de forma J si cada diagrama de forma J tiene un límite en C. Específicamente, se dice que una categoría C tiene límites de forma J.

• tiene productos si tiene límites de forma J para cada pequeña categoría discreta J (no necesita tener productos grandes),
• tiene ecualizadores si tiene límites de forma (es decir, cada par paralelo de morfismos tiene un ecualizador), ${\displaystyle \bullet \rightrightarrows \bullet }$
• tiene retrocesos si tiene límites de forma (es decir, cada par de morfismos con codominio común tiene un retroceso). ${\displaystyle \bullet \rightarrow \bullet \leftarrow \bullet }$

Una categoría completa es una categoría que tiene todos los límites pequeños (es decir, todos los límites de forma J para cada categoría pequeña J ).

También se pueden hacer definiciones duales. Una categoría tiene colímites de forma J si cada diagrama de forma J tiene un colímite en C. Una categoría cocompleta es aquella que tiene todos los colímites pequeños.

El teorema de existencia para límites establece que si una categoría C tiene ecualizadores y todos los productos indexados por las clases Ob( J ) y Hom( J ), entonces C tiene todos los límites de forma J . ^{[1] : §V.2 Teoría 1} En este caso, el límite de un diagrama F  : J → C puede construirse como el ecualizador de los dos morfismos ^{[1] : §V.2 Teoría 2}

${\displaystyle s,t:\prod _{i\in \operatorname {Ob} (J)}F(i)\rightrightarrows \prod _{f\in \operatorname {Hom} (J)}F(\operatorname {cod} (f))}$

dado (en forma de componente) por

${\displaystyle {\begin{aligned}s&={\bigl (}F(f)\circ \pi _{\operatorname {dom} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}\\t&={\bigl (}\pi _{\operatorname {cod} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}.\end{aligned}}}$

Existe un teorema de existencia dual para los colímites en términos de coecualizadores y coproductos. Ambos teoremas dan condiciones suficientes y necesarias para la existencia de todos los (co)límites de forma J .

Propiedad universal

Los límites y colímites son casos especiales importantes de construcciones universales .

Sea C una categoría y sea J una categoría de índice pequeño. La categoría de funtores C ^J puede considerarse como la categoría de todos los diagramas de forma J en C . El funtor diagonal

${\displaystyle \Delta :{\mathcal {C}}\to {\mathcal {C}}^{\mathcal {J}}}$

es el funtor que asigna cada objeto N en C al funtor constante Δ( N ) : J → C a N . Es decir, Δ( N )( X ) = N para cada objeto X en J y Δ( N )( f ) = id _N para cada morfismo f en J .

Dado un diagrama F : J → C (considerado como un objeto en C ^J ), una transformación natural ψ  : Δ( N ) → F (que es simplemente un morfismo en la categoría C ^J ) es lo mismo que un cono de N a F . Para ver esto, primero note que Δ( N )( X ) = N para todo X implica que los componentes de ψ son morfismos ψ _X  : N → F ( X ), que comparten todos el dominio N . Además, el requisito de que los diagramas del cono conmuten es verdadero simplemente porque este ψ es una transformación natural. (Dualmente, una transformación natural ψ  : F → Δ( N ) es lo mismo que un cocono de F a N .)

Por lo tanto, las definiciones de límites y colímites pueden reformularse en la forma:

• Un límite de F es un morfismo universal de Δ a F .
• Un colimite de F es un morfismo universal de F a Δ.

Adjuntos

Como todas las construcciones universales, la formación de límites y colímites es de naturaleza funcional. En otras palabras, si todo diagrama de forma J tiene un límite en C (para J pequeño) existe un funtor límite.

${\displaystyle \lim :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}}$

que asigna a cada diagrama su límite y a cada transformación natural η : F → G el único morfismo lim η : lim F → lim G conmutando con los conos universales correspondientes. Este funtor es adjunto por la derecha al funtor diagonal Δ : C → C ^J . Esta adjunción da una biyección entre el conjunto de todos los morfismos desde N hasta lim F y el conjunto de todos los conos desde N hasta F

${\displaystyle \operatorname {Hom} (N,\lim F)\cong \operatorname {Cone} (N,F)}$

lo cual es natural en las variables N y F . La unidad de esta adjunción es simplemente el cono universal de lim F a F . Si la categoría índice J es conexa (y no vacía) entonces la unidad de la adjunción es un isomorfismo de modo que lim es una inversa izquierda de Δ. Esto falla si J no es conexo. Por ejemplo, si J es una categoría discreta, los componentes de la unidad son los morfismos diagonales δ : N → N ^J .

Dualmente, si cada diagrama de forma J tiene un colimite en C (para J pequeño) existe un funtor colimite

${\displaystyle \operatorname {colim} :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}}$

que asigna a cada diagrama su colimite. Este funtor es adjunto por la izquierda al funtor diagonal Δ : C → C ^J , y uno tiene un isomorfismo natural

${\displaystyle \operatorname {Hom} (\operatorname {colim} F,N)\cong \operatorname {Cocone} (F,N).}$

La unidad de esta adjunción es el cocono universal de F a colim F. Si J está conectado (y no está vacío), entonces el cocono es un isomorfismo, de modo que colim es un inverso izquierdo de Δ.

Tenga en cuenta que tanto el functor límite como el functor colimite son functores covariantes .

Como representaciones de funtores

Se pueden usar funtores Hom para relacionar límites y colímites en una categoría C con límites en Set , la categoría de conjuntos . Esto se deduce, en parte, del hecho de que el funtor Hom covariante Hom( N , –) : C → Set preserva todos los límites en C . Por dualidad, el funtor Hom contravariante debe tomar colímites como límites.

Si un diagrama F  : J → C tiene un límite en C , denotado por lim F , existe un isomorfismo canónico

${\displaystyle \operatorname {Hom} (N,\lim F)\cong \lim \operatorname {Hom} (N,F-)}$

lo cual es natural en la variable N . Aquí el funtor Hom( N , F –) es la composición del funtor Hom Hom( N , –) con F . Este isomorfismo es el único que respeta los conos limitantes.

Se puede utilizar la relación anterior para definir el límite de F en C. El primer paso es observar que el límite del funtor Hom( N , F –) se puede identificar con el conjunto de todos los conos desde N hasta F :

${\displaystyle \lim \operatorname {Hom} (N,F-)=\operatorname {Cone} (N,F).}$

El cono límite viene dado por la familia de funciones π _X  : Cone( N , F ) → Hom( N , FX ) donde π _X ( ψ ) = ψ _X . Si se da un objeto L de C junto con un isomorfismo natural Φ  : Hom( L , –) → Cone(–, F ), el objeto L será un límite de F con el cono límite dado por Φ _L (id _L ). En lenguaje sofisticado, esto equivale a decir que un límite de F es una representación del funtor Cone(–, F ) : C → Set .

Dualmente, si un diagrama F  : J → C tiene un colimite en C , denotado colim F , existe un isomorfismo canónico único

${\displaystyle \operatorname {Hom} (\operatorname {colim} F,N)\cong \lim \operatorname {Hom} (F-,N)}$

que es natural en la variable N y respeta los conos colimitentes. Identificando el límite de Hom( F –, N ) con el conjunto Cocone( F , N ), esta relación puede usarse para definir el colimite del diagrama F como una representación del funtor Cocone( F , –).

Intercambio de límites y colimites de conjuntos

Sea I una categoría finita y J una categoría filtrada pequeña . Para cualquier bifuntor

${\displaystyle F:I\times J\to \mathbf {Set} ,}$

Hay un isomorfismo natural

${\displaystyle \operatorname {colim} \limits _{J}\lim _{I}F(i,j)\rightarrow \lim _{I}\operatorname {colim} \limits _{J}F(i,j).}$

En otras palabras, los colímites filtrados en un conjunto conmutan con límites finitos. También se cumple que los colímites pequeños conmutan con límites pequeños. ^[2]

Funciones y límites

Si F  : J → C es un diagrama en C y G  : C → D es un funtor entonces por composición (recordemos que un diagrama es simplemente un funtor) se obtiene un diagrama GF  : J → D . Una pregunta natural es entonces:

“¿Cómo se relacionan los límites de GF con los de F ?”

Preservación de límites

Un funtor G  : C → D induce una función de Cono( F ) a Cono( GF ): si Ψ es un cono de N a F entonces GΨ es un cono de GN a GF . Se dice que el funtor G preserva los límites de F si ( GL , Gφ ) es un límite de GF siempre que ( L , φ ) sea un límite de F . (Tenga en cuenta que si el límite de F no existe, entonces G preserva vacuamente los límites de F .)

Se dice que un funtor G preserva todos los límites de forma J si preserva los límites de todos los diagramas F  : J → C . Por ejemplo, se puede decir que G preserva productos, ecualizadores, pullbacks, etc. Un funtor continuo es aquel que preserva todos los límites pequeños .

Se pueden hacer definiciones análogas para los colímites. Por ejemplo, un funtor G preserva los colímites de F si G ( L , φ ) es un colímite de GF siempre que ( L , φ ) sea un colímite de F . Un funtor cocontinuo es aquel que preserva todos los colímites pequeños .

Si C es una categoría completa , entonces, por el teorema de existencia anterior para límites, un funtor G  : C → D es continuo si y solo si preserva productos (pequeños) e igualadores. Dualmente, G es cocontinuo si y solo si preserva coproductos (pequeños) y coigualadores.

Una propiedad importante de los funtores adjuntos es que cada funtor adjunto derecho es continuo y cada funtor adjunto izquierdo es cocontinuo. Como los funtores adjuntos existen en abundancia, esto da numerosos ejemplos de funtores continuos y cocontinuos.

Para un diagrama dado F  : J → C y funtor G  : C → D , si tanto F como GF tienen límites especificados, existe un morfismo canónico único

${\displaystyle \tau _{F}:G\lim F\to \lim GF}$

que respeta los conos límite correspondientes. El funtor G conserva los límites de F si y sólo si esta función es un isomorfismo. Si las categorías C y D tienen todos los límites de forma J entonces lim es un funtor y los morfismos τ _F forman los componentes de una transformación natural

${\displaystyle \tau :G\lim \to \lim G^{J}.}$

El funtor G conserva todos los límites de forma J si y solo si τ es un isomorfismo natural. En este sentido, se puede decir que el funtor G conmuta con los límites ( hasta un isomorfismo natural canónico).

La preservación de límites y colímites es un concepto que sólo se aplica a funtores covariantes . Para funtores contravariantes las nociones correspondientes serían un funtor que convierte colímites en límites, o uno que convierte límites en colímites.

Levantamiento de límites

Se dice que un funtor G  : C → D levanta límites para un diagrama F  : J → C si siempre que ( L , φ ) es un límite de GF existe un límite ( L ′, φ ′) de F tal que G ( L ′, φ ′) = ( L , φ ). Un funtor G levanta límites de forma J si levanta límites para todos los diagramas de forma J . Por lo tanto, se puede hablar de productos de elevación, ecualizadores, pullbacks, etc. Finalmente, se dice que G levanta límites si levanta todos los límites. Hay definiciones duales para el levantamiento de colimites.

Un funtor G levanta límites de forma única para un diagrama F si hay un cono de preimagen único ( L ′, φ ′) tal que ( L ′, φ ′) es un límite de F y G ( L ′, φ ′) = ( L , φ ). Se puede demostrar que G levanta límites de forma única si y solo si levanta límites y es amnésico .

La eliminación de límites está claramente relacionada con la conservación de límites. Si G elimina límites para un diagrama F y GF tiene un límite, entonces F también tiene un límite y G conserva los límites de F. De ello se deduce que:

• Si G levanta los límites de toda forma J y D tiene todos los límites de forma J , entonces C también tiene todos los límites de forma J y G conserva estos límites.
• Si G levanta todos los límites pequeños y D es completo, entonces C también es completo y G es continuo.

Las afirmaciones duales para colímites son igualmente válidas.

Creación y reflexión de límites

Sea F  : J → C un diagrama. Se dice que un funtor G  : C → D

• crear límites para F si siempre que ( L , φ ) es un límite de GF existe un único cono ( L ′, φ ′) a F tal que G ( L ′, φ ′) = ( L , φ ), y además, este cono es un límite de F .
• reflejar límites para F si cada cono a F cuya imagen bajo G es un límite de GF ya es un límite de F.

De manera dual se puede definir creación y reflexión de colimites.

Es fácil ver que las siguientes afirmaciones son equivalentes:

• El funtor G crea límites.
• El funtor G levanta límites de forma única y refleja límites.

Hay ejemplos de funtores que levantan límites de forma única pero no los crean ni los reflejan.

Ejemplos

• Todo funtor representable C → Set conserva límites (pero no necesariamente colimites). En particular, para cualquier objeto A de C , esto es cierto para el funtor covariante Hom Hom( A ,–) : C → Set .
• El funtor olvidadizo U  : Grp → Set crea (y preserva) todos los límites pequeños y colímites filtrados ; sin embargo, U no preserva los coproductos. Esta situación es típica de los funtores olvidadizos algebraicos.
• El funtor libre F  : Set → Grp (que asigna a cada conjunto S el grupo libre sobre S ) es adjunto por la izquierda al funtor olvidadizo U y es, por tanto, cocontinuo. Esto explica por qué el producto libre de dos grupos libres G y H es el grupo libre generado por la unión disjunta de los generadores de G y H .
• El funtor de inclusión Ab → Grp crea límites pero no preserva coproductos (el coproducto de dos grupos abelianos es la suma directa ).
• El functor olvidadizo Top → Set levanta límites y colimites de forma única pero no crea ninguno.
• Sea Met _c la categoría de espacios métricos con funciones continuas para morfismos. El funtor olvidadizo Met _c → Set levanta límites finitos pero no los levanta de manera unívoca.

Una nota sobre la terminología

En la terminología antigua, los límites se denominaban «límites inversos» o «límites proyectivos» y los colímites «límites directos» o «límites inductivos», lo que ha sido fuente de mucha confusión.

Hay varias formas de recordar la terminología moderna. En primer lugar,

• granos,
• coproductos,
• coecualizadores, y
• codominios

son tipos de colimits, mientras que

• granos,
• productos
• ecualizadores, y
• dominios

son tipos de límites. En segundo lugar, el prefijo "co" implica "primera variable del ". Términos como "cohomología" y "cofibración" tienen una asociación ligeramente más fuerte con la primera variable, es decir, la variable contravariante, del bifunctor. ${\displaystyle \operatorname {Hom} }$ ${\displaystyle \operatorname {Hom} }$

Véase también

• Categoría cerrada cartesiana  – Tipo de categoría en la teoría de categorías
• Ecualizador (matemáticas)  : conjunto de argumentos donde dos o más funciones tienen el mismo valor
• Límite inverso  – Construcción en teoría de categorías
• Producto (teoría de categorías)  : objeto generalizado en la teoría de categorías

Referencias

1. Mac Lane, Saunders (1998). Categorías para el matemático en activo . Textos de posgrado en matemáticas . Vol. 5 (2.ª ed.). Springer-Verlag . ISBN. 0-387-98403-8.Zbl 0906.18001  .
2. conmutatividad de límites y colimites en el n Lab

Lectura adicional

• Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Categorías abstractas y concretas (PDF) . John Wiley e hijos. ISBN 0-471-60922-6.
• Mac Lane, Saunders (1998). Categorías para el matemático en activo . Textos de posgrado en matemáticas . Vol. 5 (2.ª ed.). Springer-Verlag . ISBN. 0-387-98403-8.Zbl 0906.18001  .
• Borceux, Francis (1994). "Límites". Manual de álgebra categórica . Enciclopedia de matemáticas y sus aplicaciones 50-51, 53 [es decir, 52]. Vol. 1. Cambridge University Press. ISBN 0-521-44178-1.

Enlaces externos

• Página web interactiva que genera ejemplos de límites y colímites en la categoría de conjuntos finitos. Escrita por Jocelyn Paine.
• Límite en el laboratorio n