
La geometría algebraica es una rama de las matemáticas que utiliza técnicas algebraicas abstractas , principalmente del álgebra conmutativa , para resolver problemas geométricos . Clásicamente, estudia los ceros de polinomios multivariados ; el enfoque moderno generaliza esto en algunos aspectos diferentes.
Los objetos fundamentales de estudio en geometría algebraica son las variedades algebraicas , que son manifestaciones geométricas de soluciones de sistemas de ecuaciones polinómicas . Ejemplos de las clases más estudiadas de variedades algebraicas son líneas , círculos , parábolas , elipses , hipérbolas , curvas cúbicas como las curvas elípticas y curvas cuárticas como las lemniscatas y los óvalos de Cassini . Estas son curvas algebraicas planas . Un punto del plano se encuentra en una curva algebraica si sus coordenadas satisfacen una ecuación polinómica dada . Las preguntas básicas involucran el estudio de puntos de interés especial como puntos singulares , puntos de inflexión y puntos en el infinito . Las preguntas más avanzadas involucran la topología de la curva y la relación entre curvas definidas por diferentes ecuaciones.
La geometría algebraica ocupa un lugar central en las matemáticas modernas y tiene múltiples conexiones conceptuales con campos tan diversos como el análisis complejo , la topología y la teoría de números . Como estudio de sistemas de ecuaciones polinómicas en varias variables, el tema de la geometría algebraica comienza con la búsqueda de soluciones específicas mediante la resolución de ecuaciones , y luego procede a comprender las propiedades intrínsecas de la totalidad de las soluciones de un sistema de ecuaciones. Esta comprensión requiere tanto teoría conceptual como técnica computacional.
En el siglo XX, la geometría algebraica se dividió en varias subáreas.
Gran parte del desarrollo de la corriente principal de la geometría algebraica en el siglo XX se produjo dentro de un marco algebraico abstracto, con un énfasis creciente en las propiedades "intrínsecas" de las variedades algebraicas que no dependen de ninguna forma particular de incrustar la variedad en un espacio de coordenadas ambiental; esto es paralelo a los desarrollos en topología, geometría diferencial y compleja . Un logro clave de esta geometría algebraica abstracta es la teoría de esquemas de Grothendieck que permite utilizar la teoría de haces para estudiar las variedades algebraicas de una manera que es muy similar a su uso en el estudio de las variedades diferenciales y analíticas . Esto se obtiene extendiendo la noción de punto: En la geometría algebraica clásica, un punto de una variedad afín puede identificarse, a través del Nullstellensatz de Hilbert , con un ideal máximo del anillo de coordenadas , mientras que los puntos del esquema afín correspondiente son todos ideales primos de este anillo. Esto significa que un punto de tal esquema puede ser un punto usual o una subvariedad. Este enfoque también permite unificar el lenguaje y las herramientas de la geometría algebraica clásica, que se ocupa principalmente de los puntos complejos, y de la teoría algebraica de números. La demostración que realizó Wiles de la antigua conjetura llamada el Último Teorema de Fermat es un ejemplo del poder de este enfoque.
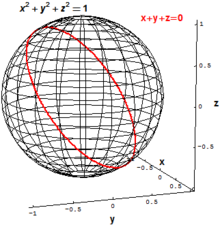
En la geometría algebraica clásica, los principales objetos de interés son los conjuntos evanescentes de conjuntos de polinomios , es decir, el conjunto de todos los puntos que satisfacen simultáneamente una o más ecuaciones polinómicas . Por ejemplo, la esfera bidimensional de radio 1 en el espacio euclidiano tridimensional R 3 podría definirse como el conjunto de todos los puntos con
Un círculo "inclinado" en R 3 se puede definir como el conjunto de todos los puntos que satisfacen las dos ecuaciones polinómicas
Primero comenzamos con un cuerpo k . En geometría algebraica clásica, este cuerpo siempre fue el de los números complejos C , pero muchos de los mismos resultados son verdaderos si asumimos solamente que k es algebraicamente cerrado . Consideramos el espacio afín de dimensión n sobre k , denotado A n ( k ) (o más simplemente A n , cuando k es claro a partir del contexto). Cuando uno fija un sistema de coordenadas, uno puede identificar A n ( k ) con k n . El propósito de no trabajar con k n es enfatizar que uno "olvida" la estructura del espacio vectorial que k n lleva .
Una función f : A n → A 1 se dice que es polinómica (o regular ) si puede escribirse como un polinomio, es decir, si existe un polinomio p en k [ x 1 ,..., x n ] tal que f ( M ) = p ( t 1 ,..., t n ) para cada punto M con coordenadas ( t 1 ,..., t n ) en A n . La propiedad de una función de ser polinómica (o regular) no depende de la elección de un sistema de coordenadas en A n .
Cuando se elige un sistema de coordenadas, las funciones regulares en el espacio n afín pueden identificarse con el anillo de funciones polinómicas en n variables sobre k . Por lo tanto, el conjunto de las funciones regulares en A n es un anillo, que se denota k [ A n ].
Decimos que un polinomio se anula en un punto si su evaluación en ese punto da cero. Sea S un conjunto de polinomios en k [ A n ]. El conjunto anulable de S (o lugar geométrico anulable o conjunto cero ) es el conjunto V ( S ) de todos los puntos en A n donde todo polinomio en S se anula. Simbólicamente,
Un subconjunto de A n que es V ( S ), para algún S , se denomina conjunto algebraico . La V representa variedad (un tipo específico de conjunto algebraico que se definirá más adelante).
Dado un subconjunto U de A n , ¿se puede recuperar el conjunto de polinomios que lo generan? Si U es cualquier subconjunto de A n , defina I ( U ) como el conjunto de todos los polinomios cuyo conjunto nulo contiene a U . La I representa un ideal : si dos polinomios f y g se nulifican en U , entonces f + g se nulifica en U , y si h es cualquier polinomio, entonces hf se nulifica en U , por lo que I ( U ) es siempre un ideal del anillo de polinomios k [ A n ].
Dos preguntas naturales que uno debe hacerse son:
La respuesta a la primera pregunta se da introduciendo la topología de Zariski , una topología sobre A n cuyos conjuntos cerrados son los conjuntos algebraicos, y que refleja directamente la estructura algebraica de k [ A n ]. Entonces U = V ( I ( U )) si y sólo si U es un conjunto algebraico o equivalentemente un conjunto cerrado por Zariski. La respuesta a la segunda pregunta la da el Nullstellensatz de Hilbert . En una de sus formas, dice que I ( V ( S )) es el radical del ideal generado por S . En un lenguaje más abstracto, hay una conexión de Galois , que da lugar a dos operadores de clausura ; pueden identificarse y, naturalmente, desempeñan un papel básico en la teoría; el ejemplo se desarrolla en Conexión de Galois.
Por diversas razones , puede que no siempre queramos trabajar con el ideal completo correspondiente a un conjunto algebraico U. El teorema de la base de Hilbert implica que los ideales en k [ A n ] siempre se generan finitamente.
Un conjunto algebraico se denomina irreducible si no puede escribirse como la unión de dos conjuntos algebraicos más pequeños. Cualquier conjunto algebraico es una unión finita de conjuntos algebraicos irreducibles y esta descomposición es única. Por lo tanto, sus elementos se denominan componentes irreducibles del conjunto algebraico. Un conjunto algebraico irreducible también se denomina variedad . Resulta que un conjunto algebraico es una variedad si y solo si puede definirse como el conjunto nulo de un ideal primo del anillo de polinomios.
Algunos autores no hacen una distinción clara entre conjuntos algebraicos y variedades y utilizan la variedad irreducible para hacer la distinción cuando es necesario.
Así como las funciones continuas son las aplicaciones naturales en espacios topológicos y las funciones suaves son las aplicaciones naturales en variedades diferenciables , existe una clase natural de funciones en un conjunto algebraico, llamadas funciones regulares o funciones polinómicas . Una función regular en un conjunto algebraico V contenido en A n es la restricción a V de una función regular en A n . Para un conjunto algebraico definido en el cuerpo de los números complejos, las funciones regulares son suaves e incluso analíticas .
Puede parecer antinaturalmente restrictivo exigir que una función regular siempre se extienda al espacio ambiental, pero es muy similar a la situación en un espacio topológico normal , donde el teorema de extensión de Tietze garantiza que una función continua en un subconjunto cerrado siempre se extiende al espacio topológico ambiental.
Al igual que las funciones regulares en el espacio afín, las funciones regulares en V forman un anillo, que denotamos por k [ V ]. Este anillo se llama anillo de coordenadas de V .
Como las funciones regulares en V provienen de funciones regulares en A n , existe una relación entre los anillos de coordenadas. Específicamente, si una función regular en V es la restricción de dos funciones f y g en k [ A n ], entonces f − g es una función polinómica que es nula en V y, por lo tanto, pertenece a I ( V ). Por lo tanto, k [ V ] puede identificarse con k [ A n ]/ I ( V ).
Usando funciones regulares de una variedad afín a A 1 , podemos definir funciones regulares de una variedad afín a otra. Primero definiremos una función regular de una variedad en un espacio afín: Sea V una variedad contenida en A n . Elijamos m funciones regulares en V , y llamémoslas f 1 , ..., f m . Definimos una función regular f de V a A m haciendo f = ( f 1 , ..., f m ) . En otras palabras, cada f i determina una coordenada del rango de f .
Si V ′ es una variedad contenida en A m , decimos que f es una función regular de V a V ′ si el rango de f está contenido en V ′.
La definición de las aplicaciones regulares se aplica también a los conjuntos algebraicos. Las aplicaciones regulares también se denominan morfismos , ya que convierten la colección de todos los conjuntos algebraicos afines en una categoría , donde los objetos son los conjuntos algebraicos afines y los morfismos son las aplicaciones regulares. Las variedades afines son una subcategoría de la categoría de los conjuntos algebraicos.
Dado un mapa regular g de V a V ′ y una función regular f de k [ V ′], entonces f ∘ g ∈ k [ V ] . El mapa f → f ∘ g es un homomorfismo de anillo de k [ V ′] a k [ V ]. Inversamente, cada homomorfismo de anillo de k [ V ′] a k [ V ] define un mapa regular de V a V ′. Esto define una equivalencia de categorías entre la categoría de conjuntos algebraicos y la categoría opuesta de las k -álgebras reducidas finitamente generadas . Esta equivalencia es uno de los puntos de partida de la teoría de esquemas .
A diferencia de las secciones anteriores, esta sección se ocupa únicamente de variedades y no de conjuntos algebraicos. Por otra parte, las definiciones se extienden naturalmente a las variedades proyectivas (siguiente sección), ya que una variedad afín y su completitud proyectiva tienen el mismo campo de funciones.
Si V es una variedad afín, su anillo de coordenadas es un dominio integral y tiene, por lo tanto, un cuerpo de fracciones que se denota k ( V ) y se llama cuerpo de las funciones racionales en V o, en breve, cuerpo de funciones de V . Sus elementos son las restricciones a V de las funciones racionales sobre el espacio afín que contiene a V . El dominio de una función racional f no es V sino el complemento de la subvariedad (una hipersuperficie) donde el denominador de f se anula.
Al igual que con los mapas regulares, se puede definir un mapa racional de una variedad V a una variedad V '. Al igual que con los mapas regulares, los mapas racionales de V a V ' pueden identificarse con los homomorfismos de campo de k ( V ') a k ( V ).
Dos variedades afines son biracionalmente equivalentes si existen entre ellas dos funciones racionales que son inversas entre sí en las regiones donde ambas están definidas. De manera equivalente, son biracionalmente equivalentes si sus campos de funciones son isomorfos.
Una variedad afín es una variedad racional si es biracionalmente equivalente a un espacio afín. Esto significa que la variedad admite una parametrización racional , es decir una parametrización con funciones racionales . Por ejemplo, el círculo de ecuación es una curva racional, pues tiene la ecuación paramétrica
que también puede verse como un mapa racional de la línea al círculo.
El problema de resolución de singularidades consiste en saber si toda variedad algebraica es birracionalmente equivalente a una variedad cuya completitud proyectiva es no singular (véase también completitud suave ). Fue resuelto afirmativamente en característica 0 por Heisuke Hironaka en 1964 y aún no se ha resuelto en característica finita.

Así como las fórmulas para las raíces de polinomios de segundo, tercer y cuarto grado sugieren extender los números reales al entorno algebraicamente más completo de los números complejos, muchas propiedades de las variedades algebraicas sugieren extender el espacio afín a un espacio proyectivo geométricamente más completo. Mientras que los números complejos se obtienen sumando el número i , una raíz del polinomio x 2 + 1 , el espacio proyectivo se obtiene agregando puntos apropiados "en el infinito", puntos donde pueden encontrarse líneas paralelas.
Para ver cómo podría suceder esto, considere la variedad V ( y − x 2 ) . Si la dibujamos, obtenemos una parábola . Cuando x tiende a infinito positivo, la pendiente de la línea desde el origen hasta el punto ( x , x 2 ) también tiende a infinito positivo. Cuando x tiende a infinito negativo, la pendiente de la misma línea tiende a infinito negativo.
Comparemos esto con la variedad V ( y − x 3 ). Esta es una curva cúbica . Cuando x tiende a infinito positivo, la pendiente de la línea desde el origen hasta el punto ( x , x 3 ) tiende a infinito positivo igual que antes. Pero a diferencia de antes, cuando x tiende a infinito negativo, la pendiente de la misma línea tiende a infinito positivo también; exactamente lo opuesto de la parábola. Por lo tanto, el comportamiento "en el infinito" de V ( y − x 3 ) es diferente del comportamiento "en el infinito" de V ( y − x 2 ).
La consideración de la terminación proyectiva de las dos curvas, que es su prolongación "en el infinito" en el plano proyectivo , permite cuantificar esta diferencia: el punto en el infinito de la parábola es un punto regular , cuya tangente es la recta en el infinito , mientras que el punto en el infinito de la curva cúbica es una cúspide . Además, ambas curvas son racionales, pues están parametrizadas por x , y el teorema de Riemann-Roch implica que la curva cúbica debe tener una singularidad, que debe estar en el infinito, pues todos sus puntos en el espacio afín son regulares.
Así, muchas de las propiedades de las variedades algebraicas, incluyendo la equivalencia biracional y todas las propiedades topológicas, dependen del comportamiento "en el infinito" y, por lo tanto, es natural estudiar las variedades en el espacio proyectivo. Además, la introducción de técnicas proyectivas hizo que muchos teoremas de la geometría algebraica fueran más simples y precisos: por ejemplo, el teorema de Bézout sobre el número de puntos de intersección entre dos variedades puede enunciarse en su forma más precisa solo en el espacio proyectivo. Por estas razones, el espacio proyectivo juega un papel fundamental en la geometría algebraica.
En la actualidad, el espacio proyectivo P n de dimensión n suele definirse como el conjunto de las rectas que pasan por un punto, considerado como origen, en el espacio afín de dimensión n + 1 , o equivalentemente al conjunto de las rectas vectoriales en un espacio vectorial de dimensión n + 1 . Cuando se ha elegido un sistema de coordenadas en el espacio de dimensión n + 1 , todos los puntos de una recta tienen el mismo conjunto de coordenadas, hasta la multiplicación por un elemento de k . Esto define las coordenadas homogéneas de un punto de P n como una sucesión de n + 1 elementos del cuerpo base k , definido hasta la multiplicación por un elemento distinto de cero de k (el mismo para toda la sucesión).
Un polinomio de n + 1 variables se anula en todos los puntos de una recta que pasa por el origen si y sólo si es homogéneo . En este caso, se dice que el polinomio se anula en el punto correspondiente de P n . Esto nos permite definir un conjunto algebraico proyectivo en P n como el conjunto V ( f 1 , ..., f k ) , donde se anula un conjunto finito de polinomios homogéneos { f 1 , ..., f k } . Al igual que para los conjuntos algebraicos afines, existe una biyección entre los conjuntos algebraicos proyectivos y los ideales homogéneos reducidos que los definen. Las variedades proyectivas son los conjuntos algebraicos proyectivos cuyo ideal definitorio es primo. En otras palabras, una variedad proyectiva es un conjunto algebraico proyectivo, cuyo anillo de coordenadas homogéneo es un dominio integral , definiéndose el anillo de coordenadas proyectivas como el cociente del anillo graduado o de los polinomios en n + 1 variables por el ideal homogéneo (reducido) que define la variedad. Todo conjunto algebraico proyectivo puede descomponerse de forma única en una unión finita de variedades proyectivas.
Las únicas funciones regulares que pueden definirse correctamente en una variedad proyectiva son las funciones constantes. Por tanto, esta noción no se utiliza en situaciones proyectivas. Por otra parte, el campo de las funciones racionales o campo de funciones es una noción útil, que, de manera similar al caso afín, se define como el conjunto de los cocientes de dos elementos homogéneos del mismo grado en el anillo de coordenadas homogéneas.
La geometría algebraica real es el estudio de las variedades algebraicas reales.
El hecho de que el campo de los números reales sea un campo ordenado no puede ignorarse en un estudio de este tipo. Por ejemplo, la curva de la ecuación es un círculo si , pero no tiene puntos reales si . La geometría algebraica real también investiga, de manera más amplia, los conjuntos semialgebraicos , que son las soluciones de sistemas de inecuaciones polinómicas. Por ejemplo, ninguna de las ramas de la hipérbola de la ecuación es una variedad algebraica real. Sin embargo, la rama en el primer cuadrante es un conjunto semialgebraico definido por y .
Un problema abierto en geometría algebraica real es la siguiente parte del decimosexto problema de Hilbert : decidir qué posiciones respectivas son posibles para los óvalos de una curva plana no singular de grado 8.
El origen de la geometría algebraica computacional se puede remontar a la reunión EUROSAM'79 (Simposio Internacional sobre Manipulación Simbólica y Algebraica) celebrada en Marsella , Francia, en junio de 1979. En esta reunión,
Desde entonces, la mayoría de los resultados en esta área están relacionados con uno o varios de estos elementos, ya sea utilizando o mejorando uno de estos algoritmos, o encontrando algoritmos cuya complejidad es simplemente exponencial en el número de variables.
En las últimas décadas se ha desarrollado un conjunto de teorías matemáticas complementarias a los métodos simbólicos, denominadas geometría algebraica numérica . El principal método computacional es la continuación de homotopía . Esto sustenta, por ejemplo, un modelo de computación en punto flotante para resolver problemas de geometría algebraica.
Una base de Gröbner es un sistema de generadores de un ideal polinomial cuyo cálculo permite la deducción de muchas propiedades de la variedad algebraica afín definida por el ideal.
Dado un ideal I que define un conjunto algebraico V :
Los cálculos de base de Gröbner no permiten calcular directamente la descomposición primaria de I ni los ideales primos que definen los componentes irreducibles de V , pero la mayoría de los algoritmos para esto implican el cálculo de base de Gröbner. Los algoritmos que no se basan en bases de Gröbner utilizan cadenas regulares , pero pueden necesitar bases de Gröbner en algunas situaciones excepcionales.
Las bases de Gröbner se consideran difíciles de calcular. De hecho, pueden contener, en el peor de los casos, polinomios cuyo grado es doblemente exponencial en el número de variables y un número de polinomios que también es doblemente exponencial. Sin embargo, esta es solo una complejidad del peor caso, y el límite de complejidad del algoritmo de Lazard de 1979 puede aplicarse con frecuencia. El algoritmo F5 de Faugère tiene en cuenta esta complejidad, ya que puede verse como una mejora del algoritmo de Lazard de 1979. De ello se deduce que las mejores implementaciones permiten realizar cálculos casi rutinariamente con conjuntos algebraicos de grado superior a 100. Esto significa que, en la actualidad, la dificultad de calcular una base de Gröbner está fuertemente relacionada con la dificultad intrínseca del problema.
CAD es un algoritmo que fue introducido en 1973 por G. Collins para implementar con una complejidad aceptable el teorema de Tarski-Seidenberg sobre eliminación de cuantificadores sobre los números reales.
Este teorema se refiere a las fórmulas de la lógica de primer orden cuyas fórmulas atómicas son igualdades polinómicas o desigualdades entre polinomios con coeficientes reales. Estas fórmulas son, por tanto, las fórmulas que pueden construirse a partir de las fórmulas atómicas mediante los operadores lógicos y (∧), o (∨), no (¬), para todo (∀) y existe (∃). El teorema de Tarski afirma que, a partir de una fórmula de este tipo, se puede calcular una fórmula equivalente sin cuantificador (∀, ∃).
La complejidad del CAD es doblemente exponencial en cuanto al número de variables. Esto significa que el CAD permite, en teoría, resolver todos los problemas de geometría algebraica real que puedan expresarse mediante una fórmula de este tipo, es decir, casi todos los problemas que conciernen a variedades explícitamente dadas y conjuntos semialgebraicos.
Mientras que el cálculo de la base de Gröbner tiene una complejidad doblemente exponencial solo en casos excepcionales, el CAD casi siempre tiene esta alta complejidad. Esto implica que, a menos que la mayoría de los polinomios que aparecen en la entrada sean lineales, es posible que no resuelva problemas con más de cuatro variables.
Desde 1973, la mayor parte de la investigación sobre este tema se dedica a mejorar el CAD o a encontrar algoritmos alternativos en casos especiales de interés general.
Como ejemplo del estado del arte, existen algoritmos eficientes para encontrar al menos un punto en cada componente conexo de un conjunto semialgebraico y, de esta manera, comprobar si un conjunto semialgebraico está vacío. Por otro lado, el CAD es, en la práctica, el mejor algoritmo para contar el número de componentes conexos.
Los algoritmos generales básicos de geometría computacional tienen una complejidad exponencial doble en el peor de los casos . Más precisamente, si d es el grado máximo de los polinomios de entrada y n el número de variables, su complejidad es como máximo para alguna constante c , y, para algunas entradas, la complejidad es como mínimo para otra constante c ′.
Durante los últimos 20 años del siglo XX, se han introducido diversos algoritmos para resolver subproblemas específicos con una mayor complejidad. La mayoría de estos algoritmos tienen una complejidad . [1]
Entre estos algoritmos que resuelven un subproblema de los problemas resueltos por las bases de Gröbner, se puede citar la comprobación de si una variedad afín es vacía y la resolución de sistemas polinómicos no homogéneos que tienen un número finito de soluciones. Dichos algoritmos rara vez se implementan porque, en la mayoría de las entradas, los algoritmos F4 y F5 de Faugère tienen una mejor eficiencia práctica y probablemente una complejidad similar o mejor ( probablemente porque la evaluación de la complejidad de los algoritmos de bases de Gröbner en una clase particular de entradas es una tarea difícil que se ha realizado solo en unos pocos casos especiales).
Los principales algoritmos de geometría algebraica real que resuelven un problema resuelto por CAD están relacionados con la topología de conjuntos semialgebraicos. Se pueden citar el conteo del número de componentes conectados , la prueba de si dos puntos están en los mismos componentes o el cálculo de una estratificación de Whitney de un conjunto algebraico real . Tienen una complejidad de , pero la constante involucrada por la notación O es tan alta que su uso para resolver cualquier problema no trivial resuelto de manera efectiva por CAD es imposible incluso si se pudiera utilizar toda la potencia de cálculo existente en el mundo. Por lo tanto, estos algoritmos nunca se han implementado y esta es un área de investigación activa para buscar algoritmos que tengan en conjunto una buena complejidad asintótica y una buena eficiencia práctica.
Los enfoques modernos de la geometría algebraica redefinen y extienden efectivamente el rango de objetos básicos en varios niveles de generalidad a esquemas, esquemas formales , esquemas ind , espacios algebraicos , pilas algebraicas , etc. La necesidad de esto surge ya de las ideas útiles dentro de la teoría de variedades, por ejemplo, las funciones formales de Zariski se pueden acomodar introduciendo elementos nilpotentes en anillos de estructura; considerando espacios de bucles y arcos, construyendo cocientes por acciones grupales y desarrollando fundamentos formales para la teoría de la intersección natural y la teoría de la deformación conducen a algunas de las extensiones posteriores.
Lo más notable es que, a principios de los años 1960, las variedades algebraicas se incluyeron en el concepto de esquema de Alexander Grothendieck . Sus objetos locales son esquemas afines o espectros primos que son espacios anillados localmente que forman una categoría que es antiequivalente a la categoría de anillos unitarios conmutativos, extendiendo la dualidad entre la categoría de variedades algebraicas afines sobre un cuerpo k y la categoría de k -álgebras reducidas finitamente generadas. La unión se realiza a lo largo de la topología de Zariski; uno puede unir dentro de la categoría de espacios anillados localmente, pero también, utilizando la incrustación de Yoneda, dentro de la categoría más abstracta de prehaces de conjuntos sobre la categoría de esquemas afines. La topología de Zariski en el sentido de la teoría de conjuntos es entonces reemplazada por una topología de Grothendieck . Grothendieck introdujo las topologías de Grothendieck teniendo en mente ejemplos más exóticos pero geométricamente más finos y sensibles que la topología de Zariski, a saber, la topología étale y las dos topologías planas de Grothendieck: fppf y fpqc; hoy en día, otros ejemplos se hicieron prominentes, incluida la topología de Nisnevich . Las haces se pueden generalizar además a pilas en el sentido de Grothendieck, generalmente con algunas condiciones de representabilidad adicionales que conducen a pilas de Artin e, incluso más finas, pilas de Deligne-Mumford , ambas a menudo llamadas pilas algebraicas.
A veces, otros sitios algebraicos sustituyen la categoría de esquemas afines. Por ejemplo, Nikolai Durov introdujo las mónadas algebraicas conmutativas como una generalización de objetos locales en una geometría algebraica generalizada. En esta configuración se realizaron versiones de una geometría tropical , de una geometría absoluta sobre un cuerpo de un elemento y un análogo algebraico de la geometría de Arakelov .
Otra generalización formal posible es la geometría algebraica universal, en la que cada variedad de álgebras tiene su propia geometría algebraica. El término variedad de álgebras no debe confundirse con variedad algebraica .
El lenguaje de esquemas, pilas y generalizaciones ha demostrado ser una forma valiosa de tratar conceptos geométricos y se ha convertido en piedras angulares de la geometría algebraica moderna.
Las pilas algebraicas se pueden generalizar aún más y para muchas cuestiones prácticas como la teoría de la deformación y la teoría de la intersección, este es a menudo el enfoque más natural. Se puede extender el sitio de Grothendieck de esquemas afines a un sitio categórico superior de esquemas afines derivados , reemplazando los anillos conmutativos con una categoría infinita de álgebras conmutativas graduadas diferenciales , o de anillos conmutativos simpliciales o una categoría similar con una variante apropiada de una topología de Grothendieck. También se pueden reemplazar prehaces de conjuntos por prehaces de conjuntos simpliciales (o de grupoides infinitos). Luego, en presencia de una maquinaria homotópica apropiada, se puede desarrollar una noción de pila derivada como tal prehaz en la categoría infinita de esquemas afines derivados, que satisface cierta versión categórica infinita de un axioma de haz (y para ser algebraico, inductivamente una secuencia de condiciones de representabilidad). Las categorías del modelo de Quillen , las categorías de Segal y las cuasicategorías son algunas de las herramientas más utilizadas para formalizar esto, lo que produce la geometría algebraica derivada , introducida por la escuela de Carlos Simpson , que incluye a Andre Hirschowitz, Bertrand Toën , Gabrielle Vezzosi, Michel Vaquié y otros; y desarrollada posteriormente por Jacob Lurie , Bertrand Toën y Gabriele Vezzosi . Otra versión (no conmutativa) de la geometría algebraica derivada, que utiliza categorías A-infinitas, ha sido desarrollada a principios de los años 1990 por Maxim Kontsevich y sus seguidores.
Algunas de las raíces de la geometría algebraica se remontan al trabajo de los griegos helenísticos del siglo V a. C. El problema de Delos , por ejemplo, consistía en construir una longitud x de modo que el cubo de lado x contuviera el mismo volumen que la caja rectangular a 2 b para los lados a y b dados . Menecmo ( c. 350 a. C. ) consideró el problema geométricamente intersectando el par de cónicas planas ay = x 2 y xy = ab . [2] En el siglo III a. C., Arquímedes y Apolonio estudiaron sistemáticamente problemas adicionales sobre secciones cónicas utilizando coordenadas. [2] [3] Apolonio, en las Cónicas, desarrolló aún más un método que es tan similar a la geometría analítica que a veces se piensa que su trabajo anticipó el trabajo de Descartes en unos 1800 años. [4] Su aplicación de líneas de referencia, un diámetro y una tangente no es esencialmente diferente de nuestro uso moderno de un marco de coordenadas, donde las distancias medidas a lo largo del diámetro desde el punto de tangencia son las abscisas, y los segmentos paralelos a la tangente e interceptados entre el eje y la curva son las ordenadas. Desarrolló aún más las relaciones entre las abscisas y las coordenadas correspondientes utilizando métodos geométricos como el uso de parábolas y curvas. [5] [6] [7] Los matemáticos medievales, incluidos Omar Khayyam , Leonardo de Pisa , Gersonides y Nicole Oresme en el Período Medieval , [8] resolvieron ciertas ecuaciones cúbicas y cuadráticas por medios puramente algebraicos y luego interpretaron los resultados geométricamente. El matemático persa Omar Khayyám (nacido en 1048 d. C.) creía que existía una relación entre la aritmética , el álgebra y la geometría . [9] [10] [11] Esto fue criticado por Jeffrey Oaks, quien afirma que el estudio de las curvas por medio de ecuaciones se originó con Descartes en el siglo XVII. [12]
Tales técnicas de aplicación de construcciones geométricas a problemas algebraicos también fueron adoptadas por varios matemáticos del Renacimiento como Gerolamo Cardano y Niccolò Fontana "Tartaglia" en sus estudios de la ecuación cúbica. El enfoque geométrico para los problemas de construcción, en lugar del algebraico, fue favorecido por la mayoría de los matemáticos de los siglos XVI y XVII, en particular Blaise Pascal , quien argumentó en contra del uso de métodos algebraicos y analíticos en geometría. [13] Los matemáticos franceses Franciscus Vieta y más tarde René Descartes y Pierre de Fermat revolucionaron la forma convencional de pensar sobre los problemas de construcción mediante la introducción de la geometría de coordenadas . Estaban interesados principalmente en las propiedades de las curvas algebraicas , como las definidas por las ecuaciones diofánticas (en el caso de Fermat), y la reformulación algebraica de las obras griegas clásicas sobre cónicas y cúbicas (en el caso de Descartes).
Durante el mismo período, Blaise Pascal y Gérard Desargues abordaron la geometría desde una perspectiva diferente, desarrollando las nociones sintéticas de la geometría proyectiva . Pascal y Desargues también estudiaron las curvas, pero desde el punto de vista puramente geométrico: el análogo de la construcción griega con regla y compás . En última instancia, triunfó la geometría analítica de Descartes y Fermat, ya que proporcionó a los matemáticos del siglo XVIII herramientas cuantitativas concretas necesarias para estudiar problemas físicos utilizando el nuevo cálculo de Newton y Leibniz . Sin embargo, a finales del siglo XVIII, la mayor parte del carácter algebraico de la geometría de coordenadas fue absorbido por el cálculo de infinitesimales de Lagrange y Euler .
Fueron necesarios los desarrollos simultáneos en el siglo XIX de la geometría no euclidiana y de las integrales abelianas para que las antiguas ideas algebraicas volvieran al ámbito geométrico. El primero de estos nuevos desarrollos fue aprovechado por Edmond Laguerre y Arthur Cayley , quienes intentaron determinar las propiedades métricas generalizadas del espacio proyectivo. Cayley introdujo la idea de formas polinómicas homogéneas , y más específicamente formas cuadráticas , en el espacio proyectivo. Posteriormente, Felix Klein estudió la geometría proyectiva (junto con otros tipos de geometría) desde el punto de vista de que la geometría en un espacio está codificada en una cierta clase de transformaciones en el espacio. A finales del siglo XIX, los geómetras proyectivos estudiaban tipos más generales de transformaciones en figuras en el espacio proyectivo. En lugar de las transformaciones lineales proyectivas que normalmente se consideraban que proporcionaban la geometría kleiniana fundamental en el espacio proyectivo, se ocuparon también de las transformaciones biracionales de grado superior . Esta noción más débil de congruencia llevaría más tarde a los miembros de la escuela italiana de geometría algebraica del siglo XX a clasificar las superficies algebraicas hasta el isomorfismo biracional .
El segundo desarrollo de principios del siglo XIX, el de las integrales abelianas, llevaría a Bernhard Riemann al desarrollo de las superficies de Riemann .
En el mismo período comenzó la algebrización de la geometría algebraica a través del álgebra conmutativa . Los resultados destacados en esta dirección son el teorema de la base de Hilbert y el Nullstellensatz de Hilbert , que son la base de la conexión entre la geometría algebraica y el álgebra conmutativa, y la resultante multivariante de Macaulay , que es la base de la teoría de la eliminación . Probablemente debido al tamaño del cálculo que implican las resultantes multivariantes, la teoría de la eliminación fue olvidada durante mediados del siglo XX hasta que fue renovada por la teoría de la singularidad y la geometría algebraica computacional. [a]
BL van der Waerden , Oscar Zariski y André Weil desarrollaron una base para la geometría algebraica basada en el álgebra conmutativa contemporánea , que incluía la teoría de la valoración y la teoría de los ideales . Uno de los objetivos era proporcionar un marco riguroso para demostrar los resultados de la escuela italiana de geometría algebraica . En particular, esta escuela utilizó sistemáticamente la noción de punto genérico sin ninguna definición precisa, que fue dada por primera vez por estos autores durante la década de 1930.
En los años 1950 y 1960, Jean-Pierre Serre y Alexander Grothendieck reformularon los fundamentos haciendo uso de la teoría de haces . Más tarde, a partir de 1960, y en gran medida liderado por Grothendieck, se elaboró la idea de esquemas , en conjunción con un aparato muy refinado de técnicas homológicas . Después de una década de rápido desarrollo, el campo se estabilizó en la década de 1970, y se hicieron nuevas aplicaciones, tanto a la teoría de números como a cuestiones geométricas más clásicas sobre variedades algebraicas, singularidades , módulos y módulos formales .
Una clase importante de variedades, que no se entienden fácilmente a partir de sus ecuaciones definitorias, son las variedades abelianas , que son las variedades proyectivas cuyos puntos forman un grupo abeliano . Los ejemplos prototípicos son las curvas elípticas , que tienen una rica teoría. Fueron fundamentales en la demostración del último teorema de Fermat y también se utilizan en la criptografía de curvas elípticas .
En paralelo con la tendencia abstracta de la geometría algebraica, que se ocupa de enunciados generales sobre variedades, también se han desarrollado métodos para el cálculo efectivo con variedades concretas dadas, que conducen a la nueva área de la geometría algebraica computacional. Uno de los métodos fundadores de esta área es la teoría de las bases de Gröbner , introducida por Bruno Buchberger en 1965. Otro método fundador, más específicamente dedicado a la geometría algebraica real, es la descomposición algebraica cilíndrica , introducida por George E. Collins en 1973.
Ver también: geometría algebraica derivada .
Una variedad analítica sobre el cuerpo de números reales o complejos se define localmente como el conjunto de soluciones comunes de varias ecuaciones que involucran funciones analíticas . Es análoga al concepto de variedad algebraica en el sentido de que lleva una estructura de haz de funciones analíticas en lugar de funciones regulares. Cualquier variedad compleja es una variedad analítica compleja. Dado que las variedades analíticas pueden tener puntos singulares , no todas las variedades analíticas complejas son variedades. Sobre un cuerpo no arquimediano, la geometría analítica se estudia a través de espacios analíticos rígidos .
La geometría analítica moderna sobre el campo de los números complejos está estrechamente relacionada con la geometría algebraica compleja, como lo ha demostrado Jean-Pierre Serre en su artículo GAGA [14] , cuyo nombre en francés significa geometría algebraica y geometría analítica . Los resultados de GAGA sobre el campo de los números complejos pueden extenderse a espacios analíticos rígidos sobre campos no arquimedianos. [15]
La geometría algebraica ahora encuentra aplicaciones en estadística , [16] teoría de control , [17] [18] robótica , [19] códigos de corrección de errores , [20] filogenética [21] y modelado geométrico . [22] También hay conexiones con la teoría de cuerdas , [23] teoría de juegos , [24] emparejamientos de grafos , [25] solitones [26] y programación entera . [27]
El propio Khayyam parece haber sido el primero en concebir una teoría general de ecuaciones cúbicas.