
La teoría de conjuntos musicales proporciona conceptos para categorizar objetos musicales y describir sus relaciones. Howard Hanson fue el primero en elaborar muchos de los conceptos para analizar la música tonal . [2] Otros teóricos, como Allen Forte , desarrollaron aún más la teoría para analizar la música atonal , [3] basándose en la teoría dodecafónica de Milton Babbitt . Los conceptos de la teoría de conjuntos musicales son muy generales y se pueden aplicar a estilos tonales y atonales en cualquier sistema de afinación de temperamento igual y, hasta cierto punto, de manera más general.
Una rama de la teoría de conjuntos musicales se ocupa de colecciones ( conjuntos y permutaciones ) de tonos y clases de tonos ( teoría de conjuntos de clases de tonos ), que pueden estar ordenados o desordenados , y pueden relacionarse mediante operaciones musicales como la transposición , la inversión melódica y la complementación. . Algunos teóricos también aplican los métodos de la teoría de conjuntos musicales al análisis del ritmo .
Aunque a menudo se piensa que la teoría de conjuntos musicales implica la aplicación de la teoría matemática de conjuntos a la música, existen numerosas diferencias entre los métodos y la terminología de las dos. Por ejemplo, los músicos usan los términos transposición e inversión mientras que los matemáticos usarían traducción y reflexión . Además, cuando la teoría musical de conjuntos se refiere a conjuntos ordenados, las matemáticas normalmente se referirían a tuplas o secuencias (aunque las matemáticas sí hablan de conjuntos ordenados , y aunque se puede considerar que estos incluyen el tipo musical en algún sentido, son mucho más complicados).
Además, la teoría musical de conjuntos está más estrechamente relacionada con la teoría de grupos y la combinatoria que con la teoría matemática de conjuntos, que se ocupa de cuestiones tales como, por ejemplo, diversos tamaños de conjuntos infinitamente grandes. En combinatoria, un subconjunto desordenado de n objetos, como clases de tono , se llama combinación , y un subconjunto ordenado, permutación . La teoría de conjuntos musicales se considera mejor como una aplicación de la combinatoria a la teoría musical que como una rama de la teoría matemática de conjuntos. Su principal conexión con la teoría matemática de conjuntos es el uso del vocabulario de la teoría de conjuntos para hablar de conjuntos finitos.
El concepto fundamental de la teoría de conjuntos musicales es el conjunto (musical), que es una colección desordenada de clases tonales. [4] Más exactamente, un conjunto de clases de tono es una representación numérica que consta de números enteros distintos (es decir, sin duplicados). [5] Los elementos de un conjunto pueden manifestarse en la música como acordes simultáneos , tonos sucesivos (como en una melodía) o ambos. [ cita necesaria ] Las convenciones de notación varían de un autor a otro, pero los conjuntos generalmente se incluyen entre llaves: {}, [6] o corchetes: []. [5]
Algunos teóricos usan corchetes angulares ⟨ ⟩ para indicar secuencias ordenadas, [7] mientras que otros distinguen conjuntos ordenados separando los números con espacios. [8] Por lo tanto, se podría anotar el conjunto desordenado de clases de tono 0, 1 y 2 (correspondientes en este caso a C, C ♯ y D) como {0,1,2}. La secuencia ordenada CC ♯ -D se anotaría ⟨0,1,2⟩ o (0,1,2). Aunque C se considera cero en este ejemplo, no siempre es así. Por ejemplo, una pieza (ya sea tonal o atonal) con un centro de tono claro de F podría analizarse de manera más útil con F establecido en cero (en cuyo caso {0,1,2} representaría F, F ♯ y G. (Por el uso de números para representar notas, ver clase de tono ).
Aunque los teóricos de conjuntos suelen considerar conjuntos de clases de tonos de temperamento igual, es posible considerar conjuntos de tonos, clases de tonos de temperamento no igual, [ cita necesaria ] inicios rítmicos o "clases de ritmo". [9] [10]
Los conjuntos de dos elementos se denominan díadas , y los conjuntos de tres elementos, tricordios (ocasionalmente "tríadas", aunque esto se confunde fácilmente con el significado tradicional de la palabra tríada ). Los conjuntos de cardinalidades superiores se denominan tetracordios (o tétradas), pentacordos (o pentadas), hexacordos (o hexadas), heptacordos (héptadas o, a veces, mezclas de raíces latinas y griegas, "septacordos", por ejemplo, Rahn ), [11] octacordos ( octadas), no acordes (nonads), decacordes (décadas), undecordes y, finalmente, el dodecordio .
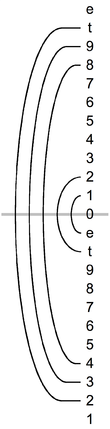
Las operaciones básicas que se pueden realizar sobre un conjunto son la transposición y la inversión . Se dice que los conjuntos relacionados por transposición o inversión están relacionados transposicionalmente o inversamente y pertenecen a la misma clase de conjunto . Dado que la transposición y la inversión son isometrías del espacio de clases de tono, preservan la estructura interválica de un conjunto, incluso si no preservan el carácter musical (es decir, la realidad física) de los elementos del conjunto. [ cita necesaria ] Este puede considerarse el postulado central de la teoría de conjuntos musicales. En la práctica, el análisis musical basado en la teoría de conjuntos consiste a menudo en la identificación de relaciones de transposición o inversión no obvias entre conjuntos que se encuentran en una pieza.
Algunos autores consideran también las operaciones de complementación y multiplicación . El complemento del conjunto X es el conjunto que consta de todas las clases de tono no contenidas en X. [12] El producto de dos clases de tono es el producto de sus números de clase de tono módulo 12. Dado que la complementación y la multiplicación no son isometrías de tono- espacio de clase, no necesariamente preservan el carácter musical de los objetos que transforman. Otros escritores, como Allen Forte, han enfatizado la relación Z , que se obtiene entre dos conjuntos que comparten el mismo contenido de intervalo total, o vector de intervalo , pero que no son equivalentes transposicional o inversamente. [13] Otro nombre para esta relación, utilizado por Hanson, [14] es "isomérico". [15]
Las operaciones en secuencias ordenadas de clases de tono también incluyen transposición e inversión, así como retrógrada y rotación . Retrogradar una secuencia ordenada invierte el orden de sus elementos. La rotación de una secuencia ordenada es equivalente a la permutación cíclica .
La transposición y la inversión se pueden representar como operaciones aritméticas elementales. Si x es un número que representa una clase de tono, su transposición en n semitonos se escribe T n = x + n mod 12. La inversión corresponde a la reflexión alrededor de algún punto fijo en el espacio de clases de tono . Si x es una clase de tono, la inversión con número de índice n se escribe In = n - x mod 12.
"Para que una relación en el conjunto S sea una relación de equivalencia [en álgebra ], tiene que satisfacer tres condiciones: tiene que ser reflexiva ..., simétrica ... y transitiva ...". [16] "De hecho, una noción informal de equivalencia siempre ha sido parte de la teoría y el análisis de la música. La teoría de conjuntos de PC, sin embargo, se ha adherido a definiciones formales de equivalencia". [17]
Se dice que dos conjuntos transposicionalmente relacionados pertenecen a la misma clase de conjunto transposicional (Tn ) . Se dice que dos conjuntos relacionados por transposición o inversión pertenecen a la misma clase de conjunto transposicional/inversional (la inversión se escribe T n I o In ) . Los conjuntos que pertenecen a la misma clase de conjuntos transposicionales suenan muy similares; mientras que los conjuntos que pertenecen a la misma clase de conjunto transposicional/inversional podrían incluir dos acordes del mismo tipo pero en diferentes tonalidades, lo que sería menos similar en sonido pero obviamente seguiría siendo una categoría limitada. Debido a esto, los teóricos de la música a menudo consideran que las clases establecidas son objetos básicos de interés musical.
Existen dos convenciones principales para nombrar clases de conjuntos de temperamento igual. Uno, conocido como número Forte , deriva de Allen Forte, cuyo The Structure of Atonal Music (1973), es uno de los primeros trabajos sobre teoría de conjuntos musicales. Forte proporcionó a cada clase de conjunto un número de la forma c – d , donde c indica la cardinalidad del conjunto y d es el número ordinal. [18] Así, el triccordo cromático {0, 1, 2} pertenece a la clase de conjunto 3-1, lo que indica que es la primera clase de conjunto de tres notas en la lista de Forte. [19] El tricordio aumentado {0, 4, 8} recibe la etiqueta 3-12, que resulta ser el último tricordio en la lista de Forte.
Las principales críticas a la nomenclatura de Forte son: (1) Las etiquetas de Forte son arbitrarias y difíciles de memorizar, y en la práctica suele ser más fácil simplemente enumerar un elemento de la clase establecida; (2) El sistema de Forte supone un temperamento igual y no puede ampliarse fácilmente para incluir conjuntos diatónicos, conjuntos de tono (a diferencia de conjuntos de clases de tono), conjuntos múltiples o conjuntos en otros sistemas de afinación; (3) El sistema original de Forte considera que los conjuntos relacionados inversamente pertenecen a la misma clase de conjunto. Esto significa que, por ejemplo, una tríada mayor y una tríada menor se consideran el mismo conjunto.
Durante siglos, la música tonal occidental ha considerado que la mayor y la menor, así como las inversiones de acordes, son significativamente diferentes. De hecho, generan objetos físicos completamente diferentes. Ignorar la realidad física del sonido es una limitación obvia de la teoría atonal. Sin embargo, se ha defendido que la teoría no se creó para llenar un vacío en el que las teorías existentes explicaban inadecuadamente la música tonal. Más bien, la teoría de Forte se utiliza para explicar la música atonal, donde el compositor ha inventado un sistema donde la distinción entre {0, 4, 7} (llamado 'mayor' en la teoría tonal) y su inversión {0, 3, 7} (llamada "menor" en la teoría tonal) puede no ser relevante.
El segundo sistema de notación etiqueta los conjuntos en términos de su forma normal , que depende del concepto de orden normal . Para poner un conjunto en orden normal, ordénelo como una escala ascendente en un espacio de clases de tono que abarque menos de una octava. Luego permute cíclicamente hasta que la primera y la última nota estén lo más juntas posible. En el caso de empates, minimice la distancia entre la primera y la penúltima nota. (En caso de empates aquí, minimice la distancia entre la primera y la penúltima nota, y así sucesivamente). Por lo tanto, {0, 7, 4} en orden normal es {0, 4, 7}, mientras que {0, 2, 10} en orden normal es {10, 0, 2}. Para poner un conjunto en forma normal, comience poniéndolo en orden normal y luego transpóngalo de modo que su primera clase de tono sea 0. [20] Los matemáticos y los informáticos suelen ordenar combinaciones utilizando el orden alfabético o binario (base dos). ordenamiento, o codificación Gray , cada uno de los cuales conduce a formas normales diferentes pero lógicas. [ cita necesaria ]
Dado que los conjuntos transposicionalmente relacionados comparten la misma forma normal, se pueden utilizar formas normales para etiquetar las clases de conjuntos T n .
Para identificar la clase de conjunto T n /I n de un conjunto:
El conjunto resultante etiqueta la clase de conjunto T n /In del conjunto inicial.
El número de operaciones distintas en un sistema que asignan un conjunto a sí mismo es el grado de simetría del conjunto . [21] El grado de simetría "especifica el número de operaciones que preservan los conjuntos de piezas desordenados de una partición; indica en qué medida los conjuntos de clases de tono de esa partición se asignan entre sí bajo transposición o inversión". [22] Cada conjunto tiene al menos una simetría, ya que se asigna a sí mismo bajo la operación de identidad T 0 . [23] Los conjuntos transposicionalmente simétricos se asignan a sí mismos para T n donde n no es igual a 0 (mod 12). Los conjuntos invertidamente simétricos se asignan a sí mismos bajo T n I. Para cualquier tipo T n /T n I dado, todos los conjuntos tienen el mismo grado de simetría. El número de conjuntos distintos en un tipo es 24 (el número total de operaciones, transposición e inversión, para n = 0 a 11) dividido por el grado de simetría del tipo T n /T n I.
Los conjuntos transposicionalmente simétricos dividen la octava de manera uniforme o pueden escribirse como la unión de conjuntos de igual tamaño que a su vez dividen la octava de manera uniforme. Los acordes inversamente simétricos son invariantes bajo reflexiones en el espacio de clases de tono. Esto significa que los acordes se pueden ordenar cíclicamente para que la serie de intervalos entre notas sucesivas sea la misma leída hacia adelante o hacia atrás. Por ejemplo, en el orden cíclico (0, 1, 2, 7), el intervalo entre la primera y la segunda nota es 1, el intervalo entre la segunda y la tercera nota es 1, el intervalo entre la tercera y la cuarta nota es 5, y el intervalo entre la cuarta nota y la primera nota es 5. [24]
Se obtiene la misma secuencia si se comienza con el tercer elemento de la serie y se retrocede: el intervalo entre el tercer elemento de la serie y el segundo es 1; el intervalo entre el segundo elemento de la serie y el primero es 1; el intervalo entre el primer elemento de la serie y el cuarto es 5; y el intervalo entre el último elemento de la serie y el tercer elemento es 5. Por lo tanto, se encuentra simetría entre T 0 y T 2 I, y hay 12 conjuntos en la clase de equivalencia T n /T n I. [24]
Fuentes