



En teoría de conjuntos musicales , un vector de intervalo es una matriz de números naturales que resumen los intervalos presentes en un conjunto de clases de tono . (Es decir, un conjunto de tonos donde se ignoran las octavas ). Otros nombres incluyen: vector ic (o vector de clase de intervalo), vector PIC (o vector de intervalo de clase de tono) y vector APIC (o vector de intervalo de clase de tono absoluto, que Michiel Schuijer afirma que es más apropiado.) [1] : 48
Si bien son principalmente una herramienta analítica, los vectores de intervalo también pueden ser útiles para los compositores, ya que muestran rápidamente las cualidades de sonido creadas por diferentes colecciones de clases de tono. Es decir, los conjuntos con altas concentraciones de intervalos convencionalmente disonantes (es decir, segundos y séptimos) suenan más disonantes, mientras que los conjuntos con un mayor número de intervalos convencionalmente consonantes (es decir, tercios y sextos) suenan más consonantes . Si bien la percepción real de consonancia y disonancia involucra muchos factores contextuales, como el registro , un vector de intervalo puede ser una herramienta útil.
En el temperamento igual de doce tonos , un vector de intervalo tiene seis dígitos, y cada dígito representa el número de veces que aparece una clase de intervalo en el conjunto. Debido a que se utilizan clases de intervalo, el vector de intervalo para un conjunto dado sigue siendo el mismo, independientemente de la permutación o disposición vertical del conjunto. Las clases de intervalo designadas por cada dígito ascienden de izquierda a derecha. Eso es:
Se omite la clase de intervalo 0, que representa unísonos y octavas.
En su libro de 1960, The Harmonic Materials of Modern Music , Howard Hanson introdujo un método monomial de notación para este concepto, al que denominó contenido interválico : p e m d n c .s b d a t f [nota 1] para lo que ahora se escribe ⟨ abcdef ⟩ . La notación moderna, introducida por Allen Forte [ ¿cuándo? ] [ cita necesaria ] , tiene ventajas considerables [ especificar ] y es extensible a cualquier división igual de la octava .
Se dice que una escala cuyo vector de intervalo tiene seis dígitos únicos tiene la propiedad de escala profunda . La escala mayor y sus modas tienen esta propiedad.
Para un ejemplo práctico, el vector de intervalo para una tríada de Do mayor ( 3-11B ) en la posición fundamental, {CEG} ( ), es ⟨001110⟩ . Esto significa que el conjunto tiene una tercera mayor o sexta menor (es decir, de C a E, o E a C), una tercera menor o sexta mayor (es decir, de E a G, o G a E) y una quinta perfecta o quinta perfecta. cuarto (es decir, de C a G, o de G a C). Como el vector de intervalo no cambia con la transposición o inversión, pertenece a toda la clase de conjunto , lo que significa que ⟨001110⟩ es el vector de todas las tríadas mayores (y menores). Algunos vectores de intervalo corresponden a más de un conjunto que no se puede transponer ni invertir para producir el otro. (Éstos se denominan conjuntos relacionados con Z, y se explican a continuación).
Para un conjunto de n clases de tono, la suma de todos los números en el vector de intervalo del conjunto es igual al número triangular T n −1 =norte × ( norte - 1)/2.
Una forma ampliada del vector de intervalo también se utiliza en la teoría de la transformación , como se establece en Generalized Musical Intervals and Transformations de David Lewin . [ se necesita cita completa ]

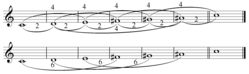
En teoría de conjuntos musicales, una relación Z , también llamada relación isomérica , es una relación entre dos conjuntos de clases de tono en la que los dos conjuntos tienen el mismo contenido interválico (y por lo tanto el mismo vector de intervalo) pero no están relacionados transposicionalmente (son de diferentes tipos T n ) o relacionados inversamente (son de diferentes tipos T n /T n I). [1] : 99 Por ejemplo, los dos conjuntos 4-z15A {0,1,4,6} y 4-z29A {0,1,3,7} tienen el mismo vector de intervalo ⟨111111⟩ pero no se puede transponer y /o invertir uno sobre el otro.
En el caso de los hexacordos , cada uno de ellos puede denominarse hexacordo Z. Cualquier hexacordo que no sea del tipo "Z" es su propio complemento , mientras que el complemento de un hexacordo Z es su correspondiente Z, por ejemplo 6-Z3 y 6-Z36. [2] Ver: 6-Z44 , 6-Z17 , 6-Z11 y número Forte .
El término, para " cigótico " ( uncido o fusión de dos células reproductivas), [1] : 98 Schuijer (2008), p.98 y 98n18. Se originó con Allen Forte en 1964, pero la noción parece haber sido considerada por primera vez por Howard Hanson. Hanson llamó a esto relación isomérica y definió dos de esos conjuntos como isoméricos . [3] Ver: isómero .
Según Michiel Schuijer (2008), el teorema del hexacordo , según el cual dos hexacordos complementarios de clase tonal cualesquiera tienen el mismo vector de intervalo, incluso si no son equivalentes bajo transposición e inversión, fue propuesto por primera vez por Milton Babbitt , y "el descubrimiento de "La relación" fue "informada" por David Lewin en 1960 como un ejemplo del teorema del complemento : que la diferencia entre intervalos de clases de tono en dos conjuntos complementarios de clases de tono es igual a la diferencia entre el número cardinal de los conjuntos. (dados dos hexacordos, esta diferencia es 0). [1] : 96–7 [4] Kassler (1961), Regener (1974) y Wilcox (1983) publicaron demostraciones matemáticas del teorema del hexacordo. [1] : 96–7
Aunque se observa comúnmente que los conjuntos relacionados con Z siempre ocurren en pares, David Lewin señaló que esto es el resultado del temperamento igual dodecafónico (12-ET). [ cita necesaria ] En 16-ET, los conjuntos relacionados con Z se encuentran como tripletes. El alumno de Lewin, Jonathan Wild, continuó este trabajo para otros sistemas de sintonización, encontrando grupos irregulares relacionados con Z con hasta 16 miembros en sistemas ET superiores. [ cita necesaria ]
La relación de equivalencia de "tener el mismo contenido de intervalo", permitiendo el caso isométrico trivial, fue inicialmente estudiada en cristalografía y se conoce como Homometría . Por ejemplo, los físicos conocen el teorema del complemento como principio de Babinet . Para una encuesta reciente ver. [5]
Straus sostiene que "[los conjuntos] en la relación Z sonarán similares porque tienen el mismo contenido de intervalo", [6] [1] : 125, lo que ha llevado a ciertos compositores a explotar la relación Z en su trabajo. Por ejemplo, la obra entre {0,1,4,6} y {0,1,3,7} es clara en el Segundo cuarteto de cuerda de Elliott Carter . [ cita necesaria ]
Algunas cuerdas relacionadas con Z están conectadas por M o IM ( multiplicación por 5 o multiplicación por 7), debido a entradas idénticas para 1 y 5 en el vector de intervalo. [1] : 83, 110