Maxwell-Boltzmann estadísticas

Distribución estadística utilizada en la mecánica de muchas partículas.

La estadística de Maxwell-Boltzmann se puede utilizar para derivar la distribución de Maxwell-Boltzmann de velocidades de partículas en un gas ideal . Se muestra: distribución de velocidades para 10 ⁶ moléculas de oxígeno a -100, 20 y 600 °C.

En mecánica estadística , la estadística de Maxwell-Boltzmann describe la distribución de partículas de materiales clásicos en varios estados de energía en equilibrio térmico . Es aplicable cuando la temperatura es lo suficientemente alta o la densidad de las partículas es lo suficientemente baja como para hacer que los efectos cuánticos sean insignificantes.

El número esperado de partículas con energía para la estadística de Maxwell-Boltzmann es ${\displaystyle \varepsilon _{i}}$

${\displaystyle \langle N_{i}\rangle ={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/kT}}}={\frac {N}{Z}}\,g_{i}e^{-\varepsilon _{i}/kT},}$

dónde:

• ${\displaystyle \varepsilon _{i}}$es la energía del i -ésimo nivel de energía ,
• ${\displaystyle \langle N_{i}\rangle }$es el número promedio de partículas en el conjunto de estados con energía , ${\displaystyle \varepsilon _{i}}$
• ${\displaystyle g_{i}}$es la degeneración del nivel de energía i , es decir, el número de estados con energía que, sin embargo, pueden distinguirse entre sí por otros medios, ^{[nb 1]} ${\displaystyle \varepsilon _{i}}$
• μ es el potencial químico ,
• k es la constante de Boltzmann ,
• T es la temperatura absoluta ,
• N es el número total de partículas:
  $${\displaystyle N=\sum _{i}N_{i},}$$
• Z es la función de partición :
  $${\displaystyle Z=\sum _{i}g_{i}e^{-\varepsilon _{i}/kT},}$$
• e es el número de Euler

De manera equivalente, el número de partículas a veces se expresa como

${\displaystyle \langle N_{i}\rangle ={\frac {1}{e^{(\varepsilon _{i}-\mu )/kT}}}={\frac {N}{Z}}\,e^{-\varepsilon _{i}/kT},}$

donde el índice i ahora especifica un estado particular en lugar del conjunto de todos los estados con energía , y . ${\displaystyle \varepsilon _{i}}$ ${\textstyle Z=\sum _{i}e^{-\varepsilon _{i}/kT}}$

Historia

Las estadísticas de Maxwell-Boltzmann surgieron de la distribución de Maxwell-Boltzmann, probablemente como una destilación de la técnica subyacente. ^{[ dudoso ]} La distribución fue deducida por primera vez por Maxwell en 1860 sobre bases heurísticas. Posteriormente, Boltzmann, en la década de 1870, llevó a cabo importantes investigaciones sobre los orígenes físicos de esta distribución. La distribución se puede derivar basándose en que maximiza la entropía del sistema.

Aplicabilidad

Comparación de la ocupación media del estado del suelo para tres estadísticas

La estadística de Maxwell-Boltzmann se utiliza para derivar la distribución de Maxwell-Boltzmann de un gas ideal. Sin embargo, también se puede utilizar para extender esa distribución a partículas con una relación energía-momento diferente , como las partículas relativistas (lo que da como resultado la distribución de Maxwell-Jüttner ), y a espacios distintos de los tridimensionales.

La estadística de Maxwell-Boltzmann se describe a menudo como la estadística de partículas clásicas "distinguibles". En otras palabras, la configuración de la partícula A en el estado 1 y la partícula B en el estado 2 es diferente del caso en el que la partícula B está en el estado 1 y la partícula A está en el estado 2. Esta suposición conduce a la estadística adecuada (de Boltzmann) de partículas en los estados de energía, pero produce resultados no físicos para la entropía, como se expresa en la paradoja de Gibbs .

Al mismo tiempo, no existen partículas reales que tengan las características requeridas por la estadística de Maxwell-Boltzmann. De hecho, la paradoja de Gibbs se resuelve si tratamos todas las partículas de un determinado tipo (por ejemplo, electrones, protones, etc.) como básicamente indistinguibles. Una vez que se hace esta suposición, las estadísticas de las partículas cambian. El cambio de entropía en el ejemplo de la entropía de la mezcla puede verse como un ejemplo de una entropía no extensiva resultante de la distinción de los dos tipos de partículas que se mezclan.

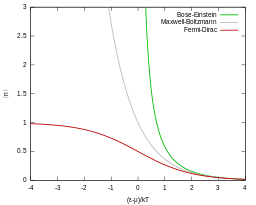
Las partículas cuánticas son bosones (siguiendo en cambio las estadísticas de Bose-Einstein ) o fermiones (sujetos al principio de exclusión de Pauli , siguiendo en cambio las estadísticas de Fermi-Dirac ). Ambas estadísticas cuánticas se acercan a las estadísticas de Maxwell-Boltzmann en el límite de alta temperatura y baja densidad de partículas.

Derivaciones

Las estadísticas de Maxwell-Boltzmann se pueden derivar en varios conjuntos termodinámicos mecánicos estadísticos : ^[1]

• El gran conjunto canónico , exactamente.
• El conjunto canónico , exactamente.
• El conjunto microcanónico , pero sólo en el límite termodinámico.

En cada caso es necesario suponer que las partículas no interactúan y que múltiples partículas pueden ocupar el mismo estado y hacerlo de forma independiente.

Derivación del conjunto microcanónico

Supongamos que tenemos un recipiente con una gran cantidad de partículas muy pequeñas, todas con características físicas idénticas (como masa, carga, etc.). Nos referiremos a esto como el sistema . Supongamos que aunque las partículas tienen propiedades idénticas, son distinguibles. Por ejemplo, podríamos identificar cada partícula observando continuamente sus trayectorias, o colocando una marca en cada una, por ejemplo dibujando un número diferente en cada una como se hace con las bolas de lotería .

Las partículas se mueven dentro de ese recipiente en todas direcciones a gran velocidad. Debido a que las partículas se mueven a gran velocidad, poseen algo de energía. La distribución de Maxwell-Boltzmann es una función matemática que describe cuántas partículas en el recipiente tienen una determinada energía. Más precisamente, la distribución de Maxwell-Boltzmann da la probabilidad no normalizada (esto significa que las probabilidades no suman 1) de que el estado correspondiente a una energía particular esté ocupado.

En general, puede haber muchas partículas con la misma cantidad de energía . Sea el número de partículas con la misma energía , el número de partículas que poseen otra energía , y así sucesivamente para todas las energías posibles. Para describir esta situación, decimos que es el número de ocupación del nivel de energía . Si conocemos todas las ocupaciones números entonces conocemos la energía total del sistema. Sin embargo, como podemos distinguir entre qué partículas ocupan cada nivel de energía, el conjunto de números de ocupación no describe completamente el estado del sistema. Para describir completamente el estado del sistema, o el microestado , debemos especificar exactamente qué partículas se encuentran en cada nivel de energía. Así, cuando contamos el número de posibles estados del sistema, debemos contar todos y cada uno de los microestados, y no sólo los posibles conjuntos de números de ocupación. ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon _{1}}$ ${\displaystyle N_{1}}$ ${\displaystyle \varepsilon _{2}}$ ${\displaystyle N_{2}}$ ${\displaystyle \{\varepsilon _{i}\mid i=1,2,3,\ldots \}.}$ ${\displaystyle N_{i}}$ ${\displaystyle i.}$ ${\displaystyle \{N_{i}\mid i=1,2,3,\ldots \},}$ ${\displaystyle \{N_{i}\mid i=1,2,3,\ldots \}}$

Para empezar, supongamos que sólo hay un estado en cada nivel de energía (no hay degeneración). Lo que sigue a continuación es un poco de pensamiento combinatorio que tiene poco que ver con la descripción precisa del depósito de partículas. Por ejemplo, digamos que hay un total de casillas etiquetadas . Con el concepto de combinación , podríamos calcular cuántas formas hay de organizar el conjunto de cajas, donde no se realiza un seguimiento del orden de las bolas dentro de cada caja. Primero, seleccionamos bolas de un total de bolas para colocarlas en la caja y continuamos seleccionando para cada caja de las bolas restantes, asegurándonos de que cada bola se coloque en una de las cajas. El número total de formas en que se pueden ordenar las bolas es ${\displaystyle i}$ ${\displaystyle k}$ ${\displaystyle a,b,\ldots ,k}$ ${\displaystyle N}$ ${\displaystyle N_{a}}$ ${\displaystyle N}$ ${\displaystyle a}$

${\displaystyle {\begin{aligned}W&={\frac {N!}{N_{a}!{\cancel {(N-N_{a})!}}}}\times {\frac {\cancel {(N-N_{a})!}}{N_{b}!{\cancel {(N-N_{a}-N_{b})!}}}}\times {\frac {\cancel {(N-N_{a}-N_{b})!}}{N_{c}!{\cancel {(N-N_{a}-N_{b}-N_{c})!}}}}\times \cdots \times {\frac {\cancel {(N-\cdots -N_{\ell })!}}{N_{k}!(N-\cdots -N_{\ell }-N_{k})!}}\\[8pt]&={\frac {N!}{N_{a}!N_{b}!N_{c}!\cdots N_{k}!(N-N_{a}-\cdots -N_{\ell }-N_{k})!}}\end{aligned}}}$

Como cada bola se ha colocado en una caja, y simplificamos la expresión como ${\displaystyle (N-N_{a}-N_{b}-\cdots -N_{k})!=0!=1}$

${\displaystyle W=N!\prod _{\ell =a,b,\ldots }^{k}{\frac {1}{N_{\ell }!}}}$

Este es solo el coeficiente multinomial , el número de formas de organizar N elementos en k cajas, la l -ésima caja que contiene N _l elementos, ignorando la permutación de elementos en cada caja.

Ahora consideremos el caso en el que hay más de una manera de poner partículas en la caja (es decir, teniendo en cuenta el problema de la degeneración). Si la -ésima caja tiene una "degeneración" de , es decir, tiene "sub-cajas" ( cajas con la misma energía . Estos estados/cajas con la misma energía se llaman estados degenerados), de modo que cualquier forma de llenar el -ésimo cuadro donde se cambia el número en los subcuadros es una forma distinta de llenar el cuadro, entonces el número de formas de llenar el i -ésimo cuadro debe incrementarse por el número de formas de distribuir los objetos en el " subcuadros". El número de formas de colocar objetos distinguibles en "subcuadros" es (el primer objeto puede ir en cualquiera de los cuadros, el segundo objeto también puede ir en cualquiera de los cuadros, y así sucesivamente). Por lo tanto, el número de formas en que un total de partículas se puede clasificar en niveles de energía según sus energías, mientras que cada nivel tiene estados distintos de modo que el i -ésimo nivel acomoda partículas es: ${\displaystyle N_{i}}$ ${\displaystyle i}$ ${\displaystyle i}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle N_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle N_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}^{N_{i}}}$ ${\displaystyle g_{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle W}$ ${\displaystyle N}$ ${\displaystyle i}$ ${\displaystyle g_{i}}$ ${\displaystyle N_{i}}$

${\displaystyle W=N!\prod _{i}{\frac {g_{i}^{N_{i}}}{N_{i}!}}}$

Esta es la forma de W derivada por primera vez por Boltzmann . La ecuación fundamental de Boltzmann relaciona la entropía termodinámica S con el número de microestados W , donde k es la constante de Boltzmann . Sin embargo, Gibbs señaló que la expresión anterior para W no produce una entropía extensa y, por tanto, es defectuosa. Este problema se conoce como la paradoja de Gibbs . El problema es que las partículas consideradas por la ecuación anterior no son indistinguibles . En otras palabras, para dos partículas ( A y B ) en dos subniveles de energía, la población representada por [A,B] se considera distinta de la población [B,A] mientras que para partículas indistinguibles, no lo son. Si llevamos a cabo el argumento a favor de partículas indistinguibles, llegamos a la expresión de Bose-Einstein para W : ${\displaystyle S=k\,\ln W}$

${\displaystyle W=\prod _{i}{\frac {(N_{i}+g_{i}-1)!}{N_{i}!(g_{i}-1)!}}}$

La distribución de Maxwell-Boltzmann se deriva de esta distribución de Bose-Einstein para temperaturas muy por encima del cero absoluto, lo que implica que . La distribución de Maxwell-Boltzmann también requiere baja densidad, lo que implica que . Bajo estas condiciones, podemos usar la aproximación de Stirling para el factorial: ${\displaystyle g_{i}\gg 1}$ ${\displaystyle g_{i}\gg N_{i}}$

${\displaystyle N!\approx N^{N}e^{-N},}$

escribir:

${\displaystyle W\approx \prod _{i}{\frac {(N_{i}+g_{i})^{N_{i}+g_{i}}}{N_{i}^{N_{i}}g_{i}^{g_{i}}}}\approx \prod _{i}{\frac {g_{i}^{N_{i}}(1+N_{i}/g_{i})^{g_{i}}}{N_{i}^{N_{i}}}}}$

Usando el hecho de que para podemos usar nuevamente la aproximación de Stirling para escribir: ${\displaystyle (1+N_{i}/g_{i})^{g_{i}}\approx e^{N_{i}}}$ ${\displaystyle g_{i}\gg N_{i}}$

${\displaystyle W\approx \prod _{i}{\frac {g_{i}^{N_{i}}}{N_{i}!}}}$

¡Esto es esencialmente una división por N ! de la expresión original de Boltzmann para W , y esta corrección se conoce comoCorrecto conteo de Boltzmann .

Deseamos encontrar el valor para el cual se maximiza la función, considerando al mismo tiempo la restricción de que hay un número fijo de partículas y una energía fija en el contenedor. Los máximos de y se logran con los mismos valores de y, dado que es más fácil de lograr matemáticamente, maximizaremos la última función. Restringimos nuestra solución usando multiplicadores de Lagrange formando la función: ${\displaystyle N_{i}}$ ${\displaystyle W}$ ${\textstyle \left(N=\sum N_{i}\right)}$ ${\textstyle \left(E=\sum N_{i}\varepsilon _{i}\right)}$ ${\displaystyle W}$ ${\displaystyle \ln(W)}$ ${\displaystyle N_{i}}$

${\displaystyle f(N_{1},N_{2},\ldots ,N_{n})=\textstyle \ln(W)+\alpha (N-\sum N_{i})+\beta (E-\sum N_{i}\varepsilon _{i})}$

${\displaystyle \ln W=\ln \left[\prod _{i=1}^{n}{\frac {g_{i}^{N_{i}}}{N_{i}!}}\right]\approx \sum _{i=1}^{n}\left(N_{i}\ln g_{i}-N_{i}\ln N_{i}+N_{i}\right)}$

Finalmente

${\displaystyle f(N_{1},N_{2},\ldots ,N_{n})=\alpha N+\beta E+\sum _{i=1}^{n}\left(N_{i}\ln g_{i}-N_{i}\ln N_{i}+N_{i}-(\alpha +\beta \varepsilon _{i})N_{i}\right)}$

Para maximizar la expresión anterior aplicamos el teorema de Fermat (puntos estacionarios) , según el cual los extremos locales, si existen, deben estar en puntos críticos (las derivadas parciales desaparecen):

${\displaystyle {\frac {\partial f}{\partial N_{i}}}=\ln g_{i}-\ln N_{i}-(\alpha +\beta \varepsilon _{i})=0}$

Resolviendo las ecuaciones anteriores ( ) llegamos a una expresión para : ${\displaystyle i=1\ldots n}$ ${\displaystyle N_{i}}$

${\displaystyle N_{i}={\frac {g_{i}}{e^{\alpha +\beta \varepsilon _{i}}}}}$

Sustituyendo esta expresión en la ecuación y suponiendo que se obtiene: ${\displaystyle N_{i}}$ ${\displaystyle \ln W}$ ${\displaystyle N\gg 1}$

${\displaystyle \ln W=(\alpha +1)N+\beta E\,}$

o, reorganizando:

${\displaystyle E={\frac {\ln W}{\beta }}-{\frac {N}{\beta }}-{\frac {\alpha N}{\beta }}}$

Boltzmann se dio cuenta de que esto es solo una expresión de la ecuación fundamental de la termodinámica integrada en Euler . Identificando E como la energía interna, la ecuación fundamental integrada de Euler establece que:

${\displaystyle E=TS-PV+\mu N}$

donde T es la temperatura , P es la presión, V es el volumen y μ es el potencial químico . La famosa ecuación de Boltzmann es la constatación de que la entropía es proporcional a siendo la constante de proporcionalidad la constante de Boltzmann . Usando la ecuación de estado del gas ideal ( PV  =  NkT ), se deduce inmediatamente que y por lo que las poblaciones ahora pueden escribirse: ${\displaystyle S=k\ln W}$ ${\displaystyle \ln W}$ ${\displaystyle \beta =1/kT}$ ${\displaystyle \alpha =-\mu /kT}$

${\displaystyle N_{i}={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/(kT)}}}}$

Tenga en cuenta que la fórmula anterior a veces se escribe:

${\displaystyle N_{i}={\frac {g_{i}}{e^{\varepsilon _{i}/kT}/z}}}$

¿ Dónde está la actividad absoluta ? ${\displaystyle z=\exp(\mu /kT)}$

Alternativamente, podemos utilizar el hecho de que

${\displaystyle \sum _{i}N_{i}=N}$

para obtener los números de población como

${\displaystyle N_{i}=N{\frac {g_{i}e^{-\varepsilon _{i}/kT}}{Z}}}$

donde Z es la función de partición definida por:

${\displaystyle Z=\sum _{i}g_{i}e^{-\varepsilon _{i}/kT}}$

En una aproximación donde ε _i se considera una variable continua, la aproximación de Thomas-Fermi produce una degeneración continua g proporcional a tal que: ${\displaystyle {\sqrt {\varepsilon }}}$

${\displaystyle {\frac {{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{\int _{0}^{\infty }{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}}={\frac {{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{{\frac {\sqrt {\pi }}{2}}(kT)^{3/2}}}={\frac {2{\sqrt {\varepsilon }}\,e^{-\varepsilon /kT}}{\sqrt {\pi (kT)^{3}}}}}$

que es simplemente la distribución de Maxwell-Boltzmann para la energía.

Derivación del conjunto canónico

En la discusión anterior, la función de distribución de Boltzmann se obtuvo analizando directamente las multiplicidades de un sistema. Alternativamente, se puede hacer uso del conjunto canónico . En un conjunto canónico, un sistema está en contacto térmico con un depósito. Si bien la energía puede fluir libremente entre el sistema y el depósito, se cree que el depósito tiene una capacidad calorífica infinitamente grande para mantener una temperatura constante, T , para el sistema combinado.

En el contexto actual, se supone que nuestro sistema tiene niveles de energía con degeneraciones . Como antes, nos gustaría calcular la probabilidad de que nuestro sistema tenga energía . ${\displaystyle \varepsilon _{i}}$ ${\displaystyle g_{i}}$ ${\displaystyle \varepsilon _{i}}$

Si nuestro sistema está en estado , entonces habría una cantidad correspondiente de microestados disponibles para el depósito. Llama a este numero . Por supuesto, el sistema combinado (del sistema que nos interesa y el yacimiento) está aislado, por lo que todos los microestados son igualmente probables. Por lo tanto, por ejemplo, si , podemos concluir que nuestro sistema tiene el doble de probabilidad de estar en estado que . En general, si es la probabilidad de que nuestro sistema esté en el estado , ${\displaystyle \;s_{1}}$ ${\displaystyle \;\Omega _{R}(s_{1})}$ ${\displaystyle \;\Omega _{R}(s_{1})=2\;\Omega _{R}(s_{2})}$ ${\displaystyle \;s_{1}}$ ${\displaystyle \;s_{2}}$ ${\displaystyle \;P(s_{i})}$ ${\displaystyle \;s_{i}}$

${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {\Omega _{R}(s_{1})}{\Omega _{R}(s_{2})}}.}$

Dado que la entropía del depósito , lo anterior se convierte en ${\displaystyle \;S_{R}=k\ln \Omega _{R}}$

${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {e^{S_{R}(s_{1})/k}}{e^{S_{R}(s_{2})/k}}}=e^{(S_{R}(s_{1})-S_{R}(s_{2}))/k}.}$

A continuación recordamos la identidad termodinámica (de la primera ley de la termodinámica ):

${\displaystyle dS_{R}={\frac {1}{T}}(dU_{R}+P\,dV_{R}-\mu \,dN_{R}).}$

En un conjunto canónico no hay intercambio de partículas, por lo que el término es cero. De manera similar, esto da ${\displaystyle dN_{R}}$ ${\displaystyle dV_{R}=0.}$

${\displaystyle S_{R}(s_{1})-S_{R}(s_{2})={\frac {1}{T}}(U_{R}(s_{1})-U_{R}(s_{2}))=-{\frac {1}{T}}(E(s_{1})-E(s_{2})),}$

donde y denotan las energías del yacimiento y del sistema en , respectivamente. Para la segunda igualdad hemos utilizado la conservación de la energía. Sustituyendo en la primera ecuación relacionada : ${\displaystyle U_{R}(s_{i})}$ ${\displaystyle E(s_{i})}$ ${\displaystyle s_{i}}$ ${\displaystyle P(s_{1}),\;P(s_{2})}$

${\displaystyle {\frac {P(s_{1})}{P(s_{2})}}={\frac {e^{-E(s_{1})/kT}}{e^{-E(s_{2})/kT}}},}$

lo que implica, para cualquier estado del sistema

${\displaystyle P(s)={\frac {1}{Z}}e^{-E(s)/kT},}$

donde Z es una "constante" elegida adecuadamente para hacer que la probabilidad total sea 1. ( Z es constante siempre que la temperatura T sea invariante).

${\displaystyle Z=\sum _{s}e^{-E(s)/kT},}$

donde el índice s recorre todos los microestados del sistema. A Z a veces se le llama suma de Boltzmann sobre estados (o "Zustandssumme" en el alemán original). Si indexamos la suma mediante los valores propios de energía en lugar de todos los estados posibles, se debe tener en cuenta la degeneración. La probabilidad de que nuestro sistema tenga energía es simplemente la suma de las probabilidades de todos los microestados correspondientes: ${\displaystyle \varepsilon _{i}}$

${\displaystyle P(\varepsilon _{i})={\frac {1}{Z}}g_{i}e^{-\varepsilon _{i}/kT}}$

donde, con modificación obvia,

${\displaystyle Z=\sum _{j}g_{j}e^{-\varepsilon _{j}/kT},}$

este es el mismo resultado que antes.

Comentarios sobre esta derivación:

• Observe que en esta formulación se prescinde del supuesto inicial "... supongamos que el sistema tiene N partículas en total...". De hecho, el número de partículas que posee el sistema no influye en la obtención de la distribución. Más bien, una consecuencia fácil es saber cuántas partículas ocuparían estados con energía . ${\displaystyle \varepsilon _{i}}$
• Lo que se ha presentado anteriormente es esencialmente una derivación de la función de partición canónica. Como se puede ver al comparar las definiciones, la suma de Boltzmann sobre estados es igual a la función de partición canónica.
• Se puede utilizar exactamente el mismo enfoque para derivar las estadísticas de Fermi-Dirac y Bose-Einstein . Sin embargo, allí se sustituiría el conjunto canónico por el gran conjunto canónico , ya que existe un intercambio de partículas entre el sistema y el depósito. Además, el sistema que se considera en esos casos es un estado de partícula única , no una partícula. (En la discusión anterior, podríamos haber asumido que nuestro sistema era un solo átomo).

Ver también

• Estadísticas de Bose-Einstein
• Fermi-Dirac estadísticas
• factor de Boltzmann

Notas

1. Por ejemplo, dos partículas puntuales simples pueden tener la misma energía, pero diferentes vectores de impulso. Se pueden distinguir unos de otros sobre esta base, y la degeneración será el número de formas posibles en que se puedan distinguir así.

Referencias

1. Tolman, RC (1938). Los principios de la mecánica estadística . Publicaciones de Dover . ISBN 9780486638966.

Bibliografía

• Carter, Ashley H., "Termodinámica clásica y estadística", Prentice – Hall, Inc., 2001, Nueva Jersey.
• Raj Pathria , "Mecánica estadística", Butterworth-Heinemann, 1996.