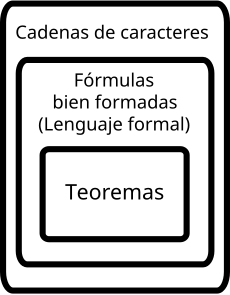
Teorema

En matemáticas, es toda proposición que, partiendo de un supuesto (hipótesis), afirma una racionabilidad (tesis) no evidente por sí misma.La conclusión del teorema es una afirmación lógica o matemática que es verdadera bajo las condiciones dadas.El contenido informativo del teorema es la relación que existe entre las hipótesis y la tesis o la conclusión.En lógica proposicional y de primer orden, cualquier afirmación demostrada se denomina teorema.Más concretamente en lógica se llama demostración a una secuencia finita de fórmulas bien formadas (fórmulas lógicas bien formadas) F1, ...,Fn, tales que cada Fi es o bien un axioma o bien un teorema que se sigue de dos fórmulas anteriores Fj y Fk (tales que jDada una demostración como la anterior si el elemento final Fn no es un axioma entonces es un teorema.Todos los teoremas se demostraban usando implícita o explícitamente estas propiedades básicas y, debido a la evidencia de estas propiedades básicas, un teorema probado se consideraba como una verdad definitiva, a menos que hubiera un error en la prueba.Esta crisis se ha resuelto revisando los fundamentos de las matemáticas para hacerlos más rigurosos.Más precisamente, si el conjunto de todos los conjuntos se puede expresar con una fórmula bien formada, esto implica que la teoría es inconsistente, y toda afirmación bien formada, así como su negación, es un teorema.Muchos teoremas matemáticos son enunciados condicionales, cuyas pruebas deducen conclusiones de condiciones conocidas como hipótesis o premisas.Aunque los teoremas se pueden escribir en una forma completamente simbólica (por ejemplo, como proposiciones en cálculo proposicional), a menudo se expresan de manera informal en un lenguaje natural como el inglés para una mejor legibilidad.Debido a que los teoremas se encuentran en el núcleo de las matemáticas, también son fundamentales para su estética.Los teoremas a menudo se describen como "triviales", "difíciles", "profundos" o incluso "hermosos".[3]​ Lógicamente, muchos teoremas tienen la forma de un indicativo condicional: Si A, entonces B.Para que un teorema sea probado, debe ser en principio expresable como un enunciado formal y preciso.Estas hipótesis forman la base fundamental de la teoría y se llaman axiomas o postulados.Algunos, por otro lado, pueden llamarse "profundos", porque sus demostraciones pueden ser largas y difíciles, involucrar áreas de las matemáticas superficialmente distintas del enunciado del teorema en sí, o mostrar conexiones sorprendentes entre áreas dispares de las matemáticas.Sin embargo, frecuentemente las áreas de conocimiento donde aparecen esas afirmaciones con frecuencia no han sido formalizadas adecuadamente en forma de sistema lógico por lo que estrictamente debería usarse con cautela el término teorema para referirse a esas afirmaciones demostrables o deducibles de supuestos «más básicos».Muchas publicaciones proporcionan instrucciones o macros para componer en el estilo interno.[13]​ El conocido aforismo, "Un matemático es un dispositivo para convertir el café en teoremas", probablemente se deba a Alfréd Rényi, aunque a menudo se atribuye al colega de Rényi Paul Erdős (y Rényi puede haber estado pensando en Erdős), que era famoso por los muchos teoremas que produjo, el número de sus colaboraciones y su consumo de café.