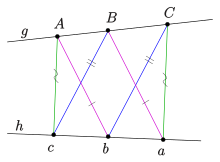
Teorema del hexágono de Pappus
En matemáticas, el teorema del hexágono de Pappus (atribuido al matemático griego Pappus de Alejandría) afirma que:[1] Dados tres puntos distintos
, respectivamente, están alineados en la denominada recta de Pappus.
Estos tres puntos son los puntos de intersección de los lados "opuestos" del hexágono
[2] Los planos proyectivos en los que se satisface el teorema de Pappus se denominan planos pappusianos.
Si se restringe el plano proyectivo a un plano afín de forma que la recta de Pappus (
en el dibujo) sea la recta del infinito, se obtiene la versión afín del mismo mostrada en el segundo dibujo.
El teorema de Pappus es un caso particular del teorema de Pascal, que afirma lo mismo para cualquier cónica.
Por el principio de dualidad en los espacios proyectivos, el teorema de Pappus induce otro teorema cierto en geometría proyectiva: su dual.
El dual del teorema de Pappus enuncia que, dadas tres rectas concurrentes
Además, introducido como axioma permite demostrar todos los teoremas de incidencia conocidos sin tener que introducir axiomas métricos.
La versión afín del teorema a la que nos referimos es aquella que se obtiene al tomar la recta de Pappus como la recta del infinito.
son puntos del infinito, es decir, que
Si se demuestra la versión afín del teorema, entonces la versión proyectiva queda a su vez demostrada, pues podemos recuperar la configuración proyectiva original ya que la extensión de un plano pappusiano a un plano proyectivo es única.
Por el posible paralelismo en los espacios afines, hace falta distinguir dos casos:
son paralelas (no iguales).Fijamos la referencia afín de centro
, pues ambas tienen puntos de primera coordenada constante.Esto termina la demostración del caso afín y, completando este al espacio proyectivo añadiendo la recta del infinito, tenemos la versión proyectiva demostrada.
Tenemos las siguientes transformaciones: Consideremos ahora la proyección central
y transforma los puntos como sigue: Consideremos ahora la proyección central
Si lo estuvieran bastaría tomar otra referencia de la misma forma y proceder análogamente.
Calculamos las coordenadas (salvo producto por escalar, indicado por los corchetes) de los puntos involucrados:
Si el producto es conmutativo (que lo es, porque en principio estamos en un cuerpo), hemos acabado, porque ya hemos visto que
El teorema de Pappus tiene varias versiones afines que se deducen de la versión proyectiva eligiendo distintas rectas del infinito.
En el espacio afín, suponemos, como en la versión proyectiva, que
La versión en que estas rectas son paralelas es la versión afín demostrada en el primer apartado (con la recta de Pappus en el infinito).
Por la versión proyectiva del teorema, deducimos que
Sin embargo, añadiendo ciertas condiciones, podemos dar una demostración puramente afín de esta versión a partir del teorema de Menelao.
Estas condiciones añadidas son las siguientes: suponemos que
y, por tanto, definen un triángulo (en azul en la figura).
Observamos que Por el teorema de Menelao, estas alineaciones se traducen en las siguientes igualdades:
Multiplicando estas igualdades, el miembro izquierdo se simplifica y queda