Se encuentra que materiales magnéticos con interacción espín-órbita fuerte, tales como: LaFeAsO,[1] PrFe4P12[2] , YbRu2Ge2,[3] UO2,[4] NpO2,[5] Ce1−xLaxB6,[6] URu2Si2[7] y muchos otros compuestos tienen un ordenamiento magnético constituido por multipolos de alto rango (cuádruple, óctuple, etc).[8] Debido al fuerte acoplamiento espín-órbita, los multipolos se presentan automáticamente en sistemas donde el número cuántico de momento angular total, J, es mayor que 1/2.Además del ordenamiento multipolar, se cree que muchos otros fenómenos ocultos están estrechamente relacionados con las interacciones multipolares.Considérese un sistema mecano-cuántico con un espacio de Hilbert generado porEntonces cualquier operador cuántico puede representarse usando el conjunto basematrices para expandir completamente cualquier operador cuántico en este espacio de Hilbert.Tomando como ejemplo J=1/2, un operador A se puede expandir como Obviamente, las matrices:De hecho, esta no es la única superbase que permite el truco.comparten las mismas propiedades rotacionales que los tensores armónicos esféricos de rango 1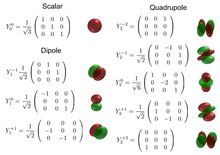también están descritos por funciones armónicas esféricas o cúbicas, se puede imaginar o visualizar estos operadores usando las funciones de onda de orbitales atómicos, a pesar de que son esencialmente matrices y no funciones espaciales.{\displaystyle \lbrace T_{s},T_{x},T_{y},T_{z},T_{xy},T_{yz},T_{zx},T_{x^{2}-y^{2}},T_{3z^{2}-r^{2}}\rbrace }se conoce como tensor escalar o de rango 0, losse conocen como tensores dipolares o de rango 1 y losSe conocen como tensores cuadrupolares o de rango 2.Este ejemplo muestra que, para un problema de multipletepresentará automáticamente multipolos de alto rango en el sistema.se puede expresar como donde el paréntesis denota un símbolo 3-j; K es el rango que varía entre; Q es el índice de proyección del rango K que varía entre -K y +K.puede expandirse como donde los coeficientes de la expansión se pueden obtener tomando la traza, esto es,Aparentemente, se pueden hacer combinaciones lineales de estos operadores para formar una nueva superbase que tenga diferentes simetrías.Por ejemplo, para los operadores tensoriales armónicos esféricos del casose convierte ahora en dos pasos de transición dipolares aún mayor, se pueden esperar términos de autointercambio más complicados.Existen cuatro mecanismos principales para inducir interacciones de intercambio entre dos momentos magnéticos en un sistema: intercambio directo, RKKY, superintercambio y red de espines.Una característica importante del hamiltoniano de intercambio multipolar es su anisotropía., si se gira el eje z realizando una rotación deAsí, una definición sugerida del antiferromagnetismo multipolar es girar sus fases enAunque ha habido muchos trabajos basados en ajustar los hamiltonianos modelo con los experimentos, aún no se han obtenido predicciones de las constantes de acoplamiento basadas en primeros principios.[10] Más tarde, se desarrolló una aproximación de primeros principios para estimar los parámetros que obtuvo un buen ajuste con unos pocos compuestos, como ciertos compuestos de cerio.[11] Una nueva aproximación por primeros principios se propuso en los años 2010.
Elementos de matriz y parte real de las funciones armónicas correspondientes de la base de operadores cúbica en el caso J=1.
Cambio de fase de los multipolos.
Cadenas de ordenamiento antiferromagnético de diferentes multipolos.
