
En matemáticas , una serie temporal es una serie de puntos de datos indexados (o enumerados o graficados) en orden cronológico. Por lo general, una serie temporal es una secuencia tomada en puntos sucesivos igualmente espaciados en el tiempo. Por lo tanto, es una secuencia de datos de tiempo discreto . Algunos ejemplos de series temporales son las alturas de las mareas oceánicas , los recuentos de manchas solares y el valor de cierre diario del Promedio Industrial Dow Jones .
Las series temporales se representan con mucha frecuencia mediante un gráfico de series temporales (que es un gráfico de líneas temporales ). Las series temporales se utilizan en estadística , procesamiento de señales , reconocimiento de patrones , econometría , finanzas matemáticas , pronóstico del tiempo , predicción de terremotos , electroencefalografía , ingeniería de control , astronomía , ingeniería de comunicaciones y, en gran medida, en cualquier dominio de la ciencia aplicada y la ingeniería que involucre mediciones temporales .
El análisis de series temporales comprende métodos para analizar datos de series temporales con el fin de extraer estadísticas significativas y otras características de los datos. La previsión de series temporales es el uso de un modelo para predecir valores futuros en función de valores observados previamente. Por lo general, los datos de series temporales se modelan como un proceso estocástico . Si bien el análisis de regresión se emplea a menudo de manera tal que se prueben las relaciones entre una o más series temporales diferentes, este tipo de análisis no suele denominarse "análisis de series temporales", que se refiere en particular a las relaciones entre diferentes puntos en el tiempo dentro de una sola serie.
Los datos de series temporales tienen un orden temporal natural. Esto hace que el análisis de series temporales sea distinto de los estudios transversales , en los que no hay un orden natural de las observaciones (por ejemplo, explicar los salarios de las personas en función de sus respectivos niveles educativos, donde los datos de los individuos podrían ingresarse en cualquier orden). El análisis de series temporales también es distinto del análisis de datos espaciales , donde las observaciones generalmente se relacionan con ubicaciones geográficas (por ejemplo, contabilizar los precios de las viviendas en función de la ubicación, así como de las características intrínsecas de las viviendas). Un modelo estocástico para una serie temporal generalmente reflejará el hecho de que las observaciones cercanas en el tiempo estarán más estrechamente relacionadas que las observaciones más separadas. Además, los modelos de series temporales a menudo harán uso del orden natural unidireccional del tiempo, de modo que los valores para un período determinado se expresarán como derivados de alguna manera de valores pasados, en lugar de valores futuros (véase reversibilidad temporal ).
El análisis de series de tiempo se puede aplicar a datos continuos de valor real , datos numéricos discretos o datos simbólicos discretos (es decir, secuencias de caracteres, como letras y palabras en el idioma inglés [1] ).
Los métodos para el análisis de series temporales pueden dividirse en dos clases: métodos de dominio de frecuencia y métodos de dominio de tiempo . Los primeros incluyen el análisis espectral y el análisis wavelet ; los segundos incluyen el análisis de autocorrelación y correlación cruzada . En el dominio del tiempo, la correlación y el análisis pueden realizarse de manera similar a un filtro utilizando correlación escalada , mitigando así la necesidad de operar en el dominio de frecuencia.
Además, las técnicas de análisis de series temporales pueden dividirse en métodos paramétricos y no paramétricos . Los métodos paramétricos suponen que el proceso estocástico estacionario subyacente tiene una determinada estructura que puede describirse utilizando un pequeño número de parámetros (por ejemplo, utilizando un modelo autorregresivo o de media móvil ). En estos métodos, la tarea consiste en estimar los parámetros del modelo que describe el proceso estocástico. Por el contrario, los métodos no paramétricos estiman explícitamente la covarianza o el espectro del proceso sin suponer que el proceso tenga una estructura particular.
Los métodos de análisis de series de tiempo también pueden dividirse en lineales y no lineales , y univariados y multivariados .
Una serie temporal es un tipo de datos de panel . Los datos de panel son la clase general, un conjunto de datos multidimensionales, mientras que un conjunto de datos de serie temporal es un panel unidimensional (como lo es un conjunto de datos transversales ). Un conjunto de datos puede exhibir características tanto de datos de panel como de datos de serie temporal. Una forma de saberlo es preguntar qué hace que un registro de datos sea único con respecto a los otros registros. Si la respuesta es el campo de datos de tiempo, entonces este es un candidato a conjunto de datos de serie temporal. Si la determinación de un registro único requiere un campo de datos de tiempo y un identificador adicional que no está relacionado con el tiempo (por ejemplo, identificación del estudiante, símbolo bursátil, código de país), entonces es un candidato a datos de panel. Si la diferenciación radica en el identificador no relacionado con el tiempo, entonces el conjunto de datos es un candidato a conjunto de datos transversales.
Hay varios tipos de motivación y análisis de datos disponibles para series de tiempo que son apropiados para diferentes propósitos.
En el contexto de la estadística , la econometría , las finanzas cuantitativas , la sismología , la meteorología y la geofísica, el objetivo principal del análisis de series temporales es la previsión . En el contexto del procesamiento de señales , la ingeniería de control y la ingeniería de comunicaciones , se utiliza para la detección de señales. Otras aplicaciones son la minería de datos , el reconocimiento de patrones y el aprendizaje automático , donde el análisis de series temporales se puede utilizar para la agrupación , [2] [3] la clasificación , [4] la consulta por contenido, [5] la detección de anomalías y la previsión . [6]

Una forma sencilla de examinar una serie temporal regular es manualmente con un gráfico de líneas . El datagráfico muestra las muertes por tuberculosis en los Estados Unidos, [7] junto con el cambio anual y el cambio porcentual de un año a otro. El número total de muertes disminuyó cada año hasta mediados de la década de 1980, después de lo cual hubo aumentos ocasionales, a menudo proporcionalmente, pero no absolutamente, bastante grandes.
Un estudio de analistas de datos corporativos encontró dos desafíos para el análisis exploratorio de series de tiempo: descubrir la forma de patrones interesantes y encontrar una explicación para estos patrones. [8] Las herramientas visuales que representan datos de series de tiempo como matrices de mapas de calor pueden ayudar a superar estos desafíos.
Otras técnicas incluyen:
El ajuste de curvas [11] [12] es el proceso de construcción de una curva o función matemática que se ajuste mejor a una serie de puntos de datos , [13] posiblemente sujeta a restricciones. [14] [15] El ajuste de curvas puede implicar interpolación , [16] [17] donde se requiere un ajuste exacto a los datos, o suavizado , [18] [19] en el que se construye una función "suave" que se ajusta aproximadamente a los datos. Un tema relacionado es el análisis de regresión , [20] [21] que se centra más en cuestiones de inferencia estadística como cuánta incertidumbre está presente en una curva que se ajusta a los datos observados con errores aleatorios. Las curvas ajustadas se pueden utilizar como ayuda para la visualización de datos, [22] [23] para inferir valores de una función cuando no hay datos disponibles, [24] y para resumir las relaciones entre dos o más variables. [25] La extrapolación se refiere al uso de una curva ajustada más allá del rango de los datos observados, [26] y está sujeta a un grado de incertidumbre [27] ya que puede reflejar el método utilizado para construir la curva tanto como refleja los datos observados.
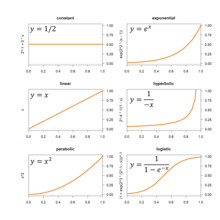
Para los procesos que se espera que generalmente crezcan en magnitud, se puede ajustar una de las curvas del gráfico (y muchas otras) estimando sus parámetros.
La construcción de series temporales económicas implica la estimación de algunos componentes para algunas fechas mediante la interpolación entre valores ("puntos de referencia") para fechas anteriores y posteriores. La interpolación es la estimación de una cantidad desconocida entre dos cantidades conocidas (datos históricos) o la extracción de conclusiones sobre la información faltante a partir de la información disponible ("leer entre líneas"). [28] La interpolación es útil cuando los datos que rodean a los datos faltantes están disponibles y se conocen su tendencia, estacionalidad y ciclos a largo plazo. Esto se hace a menudo utilizando una serie relacionada conocida para todas las fechas relevantes. [29] Alternativamente, se utiliza la interpolación polinómica o la interpolación spline donde las funciones polinómicas por partes se ajustan en intervalos de tiempo de modo que encajen suavemente entre sí. Un problema diferente que está estrechamente relacionado con la interpolación es la aproximación de una función complicada por una función simple (también llamada regresión ). La principal diferencia entre regresión e interpolación es que la regresión polinómica da un solo polinomio que modela todo el conjunto de datos. Sin embargo, la interpolación spline produce una función continua por partes compuesta de muchos polinomios para modelar el conjunto de datos.
La extrapolación es el proceso de estimar, más allá del rango de observación original, el valor de una variable en función de su relación con otra variable. Es similar a la interpolación , que produce estimaciones entre observaciones conocidas, pero la extrapolación está sujeta a una mayor incertidumbre y a un mayor riesgo de producir resultados sin sentido.
En general, un problema de aproximación de funciones nos pide seleccionar una función entre una clase bien definida que coincida estrechamente ("se aproxime") a una función objetivo de una manera específica de la tarea. Se pueden distinguir dos clases principales de problemas de aproximación de funciones: primero, para funciones objetivo conocidas, la teoría de aproximación es la rama del análisis numérico que investiga cómo ciertas funciones conocidas (por ejemplo, funciones especiales ) pueden aproximarse mediante una clase específica de funciones (por ejemplo, polinomios o funciones racionales ) que a menudo tienen propiedades deseables (computación económica, continuidad, valores integrales y límite, etc.).
En segundo lugar, la función objetivo, llamémosla g , puede ser desconocida; en lugar de una fórmula explícita, solo se proporciona un conjunto de puntos (una serie temporal) de la forma ( x , g ( x )). Dependiendo de la estructura del dominio y el codominio de g , pueden ser aplicables varias técnicas para aproximar g . Por ejemplo, si g es una operación sobre los números reales , se pueden utilizar técnicas de interpolación , extrapolación , análisis de regresión y ajuste de curvas . Si el codominio (rango o conjunto objetivo) de g es un conjunto finito, se está tratando con un problema de clasificación . Un problema relacionado con la aproximación de series temporales en línea [30] es resumir los datos en una sola pasada y construir una representación aproximada que pueda soportar una variedad de consultas de series temporales con límites en el error del peor de los casos.
Hasta cierto punto, los diferentes problemas ( regresión , clasificación , aproximación de aptitud ) han recibido un tratamiento unificado en la teoría del aprendizaje estadístico , donde se los considera problemas de aprendizaje supervisado .
En estadística , la predicción es una parte de la inferencia estadística . Un enfoque particular de dicha inferencia se conoce como inferencia predictiva , pero la predicción puede llevarse a cabo dentro de cualquiera de los diversos enfoques de la inferencia estadística. De hecho, una descripción de la estadística es que proporciona un medio para transferir conocimiento sobre una muestra de una población a toda la población y a otras poblaciones relacionadas, lo que no es necesariamente lo mismo que la predicción a lo largo del tiempo. Cuando la información se transfiere a lo largo del tiempo, a menudo a puntos específicos en el tiempo, el proceso se conoce como pronóstico .
Asignar un patrón de series de tiempo a una categoría específica, por ejemplo, identificar una palabra basándose en una serie de movimientos de la mano en lenguaje de señas .
Este enfoque se basa en el análisis armónico y el filtrado de señales en el dominio de la frecuencia utilizando la transformada de Fourier y la estimación de la densidad espectral , cuyo desarrollo se aceleró significativamente durante la Segunda Guerra Mundial por el matemático Norbert Wiener , los ingenieros eléctricos Rudolf E. Kálmán , Dennis Gabor y otros para filtrar señales del ruido y predecir los valores de la señal en un punto determinado en el tiempo. Véase Filtro de Kalman , Teoría de la estimación y Procesamiento de señales digitales
División de una serie temporal en una secuencia de segmentos. A menudo, una serie temporal se puede representar como una secuencia de segmentos individuales, cada uno con sus propias propiedades características. Por ejemplo, la señal de audio de una llamada en conferencia se puede dividir en fragmentos correspondientes a los momentos en los que cada persona estaba hablando. En la segmentación de series temporales, el objetivo es identificar los puntos límite de los segmentos en la serie temporal y caracterizar las propiedades dinámicas asociadas con cada segmento. Se puede abordar este problema mediante la detección de puntos de cambio o modelando la serie temporal como un sistema más sofisticado, como un sistema lineal de saltos de Markov.
Los datos de series temporales se pueden agrupar, sin embargo se debe tener especial cuidado al considerar la agrupación de subsecuencias. [32] La agrupación de series temporales se puede dividir en
La agrupación de series temporales de subsecuencia dio como resultado agrupaciones inestables (aleatorios) inducidas por la extracción de características utilizando fragmentación con ventanas deslizantes. [33] Se encontró que los centros de los agrupamientos (el promedio de las series temporales en un agrupamiento, también una serie temporal) siguen un patrón sinusoidal desplazado arbitrariamente (independientemente del conjunto de datos, incluso en las realizaciones de un paseo aleatorio ). Esto significa que los centros de los agrupamientos encontrados no son descriptivos para el conjunto de datos porque los centros de los agrupamientos son siempre ondas sinusoidales no representativas.
Los modelos para datos de series temporales pueden tener muchas formas y representar diferentes procesos estocásticos . Al modelar variaciones en el nivel de un proceso, tres amplias clases de importancia práctica son los modelos autorregresivos (AR), los modelos integrados (I) y los modelos de promedio móvil (MA). Estas tres clases dependen linealmente de puntos de datos anteriores. [34] Las combinaciones de estas ideas producen modelos autorregresivos de promedio móvil (ARMA) y modelos autorregresivos de promedio móvil integrado (ARIMA). El modelo autorregresivo de promedio móvil integrado fraccionalmente (ARFIMA) generaliza los tres anteriores. Las extensiones de estas clases para tratar con datos con valores vectoriales están disponibles bajo el encabezado de modelos de series temporales multivariados y, a veces, las siglas anteriores se extienden incluyendo una "V" inicial para "vector", como en VAR para autorregresión vectorial . Existe un conjunto adicional de extensiones de estos modelos que se pueden utilizar cuando la serie temporal observada está determinada por alguna serie temporal "forzada" (que puede no tener un efecto causal en la serie observada): la distinción con el caso multivariado es que la serie forzada puede ser determinista o estar bajo el control del experimentador. Para estos modelos, las siglas se extienden con una "X" final para "exógena".
La dependencia no lineal del nivel de una serie con respecto a los puntos de datos anteriores es de interés, en parte debido a la posibilidad de producir una serie temporal caótica . Sin embargo, lo que es más importante, las investigaciones empíricas pueden indicar la ventaja de utilizar predicciones derivadas de modelos no lineales, en lugar de las de modelos lineales, como por ejemplo en los modelos exógenos autorregresivos no lineales . Otras referencias sobre análisis de series temporales no lineales: (Kantz y Schreiber), [35] y (Abarbanel) [36]
Entre otros tipos de modelos de series temporales no lineales, existen modelos para representar los cambios de varianza a lo largo del tiempo ( heteroscedasticidad ). Estos modelos representan heteroscedasticidad condicional autorregresiva (ARCH) y la colección comprende una amplia variedad de representaciones ( GARCH , TARCH, EGARCH, FIGARCH, CGARCH, etc.). Aquí los cambios en la variabilidad están relacionados con, o predichos por, valores pasados recientes de la serie observada. Esto contrasta con otras posibles representaciones de variabilidad que varía localmente, donde la variabilidad podría modelarse como impulsada por un proceso separado que varía en el tiempo, como en un modelo doblemente estocástico .
En trabajos recientes sobre análisis sin modelos, los métodos basados en transformadas wavelet (por ejemplo, wavelets localmente estacionarios y redes neuronales descompuestas por wavelets) han ganado popularidad. [37] Las técnicas multiescala (a menudo denominadas multiresolución) descomponen una serie temporal dada, intentando ilustrar la dependencia temporal en múltiples escalas. Véase también técnicas multifractales de conmutación de Markov (MSMF) para modelar la evolución de la volatilidad.
Un modelo oculto de Markov (HMM) es un modelo estadístico de Markov en el que se supone que el sistema que se modela es un proceso de Markov con estados no observados (ocultos). Un HMM puede considerarse como la red bayesiana dinámica más simple . Los modelos HMM se utilizan ampliamente en el reconocimiento de voz , para traducir una serie temporal de palabras habladas en texto.
Muchos de estos modelos se recopilan en el paquete de Python sktime.
Se utilizan varias notaciones diferentes para el análisis de series temporales. Una notación común que especifica una serie temporal X indexada por los números naturales se escribe
Otra notación común es
donde T es el conjunto de índices .
Hay dos conjuntos de condiciones bajo las cuales se construye gran parte de la teoría:
La ergodicidad implica estacionariedad, pero lo inverso no es necesariamente el caso. La estacionariedad suele clasificarse en estacionariedad estricta y estacionariedad de sentido amplio o de segundo orden . Tanto los modelos como las aplicaciones pueden desarrollarse en cada una de estas condiciones, aunque los modelos en el último caso podrían considerarse como parcialmente especificados.
Además, el análisis de series temporales se puede aplicar cuando las series son estacionalmente estacionarias o no estacionarias. Las situaciones en las que las amplitudes de los componentes de frecuencia cambian con el tiempo se pueden abordar mediante el análisis de tiempo-frecuencia, que utiliza una representación de tiempo-frecuencia de una serie temporal o señal. [38]
Las herramientas para investigar datos de series temporales incluyen:
Métricas o características de series temporales que se pueden utilizar para la clasificación de series temporales o el análisis de regresión : [41]
Las series temporales se pueden visualizar con dos categorías de gráficos: gráficos superpuestos y gráficos separados. Los gráficos superpuestos muestran todas las series temporales en el mismo diseño, mientras que los gráficos separados las presentan en diferentes diseños (pero alineadas para fines de comparación) [45]
estas funciones se cumplen si tenemos un ajuste bueno a moderado para los datos observados.