Caminata aleatoria

Formalización matemática de un camino que consta de una sucesión de pasos aleatorios.

Cinco paseos aleatorios de ocho pasos desde un punto central. Algunos caminos parecen tener menos de ocho pasos donde la ruta se ha doblado sobre sí misma. ( versión animada )

En matemáticas , un paseo aleatorio , a veces conocido como paseo del borracho , es un proceso aleatorio que describe un camino que consta de una sucesión de pasos aleatorios en algún espacio matemático .

Un ejemplo elemental de paseo aleatorio es el paseo aleatorio sobre la recta numérica entera que comienza en 0 y en cada paso se mueve +1 o −1 con igual probabilidad . Otros ejemplos incluyen el camino que sigue una molécula mientras viaja en un líquido o gas (ver movimiento browniano ), el camino de búsqueda de un animal en busca de alimento o el precio de una acción fluctuante y el estado financiero de un jugador . Los paseos aleatorios tienen aplicaciones en la ingeniería y en muchos campos científicos, incluidos la ecología , la psicología , la informática , la física , la química , la biología , la economía y la sociología . El término paseo aleatorio fue introducido por primera vez por Karl Pearson en 1905. ^[1] ${\displaystyle \mathbb {Z} }$

Las realizaciones de paseos aleatorios se pueden obtener mediante simulación de Monte Carlo . ^[2]

Paseo aleatorio de celosía

Un modelo popular de paseo aleatorio es el de un paseo aleatorio sobre una red regular, donde en cada paso la ubicación salta a otro sitio de acuerdo con alguna distribución de probabilidad. En un paseo aleatorio simple , la ubicación sólo puede saltar a sitios vecinos de la red, formando un camino de red . En un paseo aleatorio simétrico simple sobre una red localmente finita, las probabilidades de que la ubicación salte a cada uno de sus vecinos inmediatos son las mismas. El ejemplo mejor estudiado es el paseo aleatorio en la red de enteros d -dimensionales (a veces llamada red hipercúbica) . ^[3] ${\displaystyle \mathbb {Z} ^{d}}$

Si el espacio de estados está limitado a dimensiones finitas, el modelo de paseo aleatorio se denomina paseo aleatorio simétrico con bordes simples , y las probabilidades de transición dependen de la ubicación del estado porque en los estados de margen y esquina el movimiento es limitado. ^[4]

Paseo aleatorio unidimensional

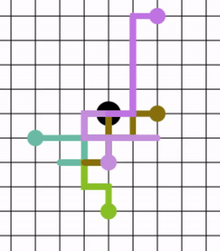
Un ejemplo elemental de paseo aleatorio es el paseo aleatorio sobre la recta numérica entera , que comienza en 0 y en cada paso se mueve +1 o −1 con igual probabilidad. ${\displaystyle \mathbb {Z} }$

Este paseo se puede ilustrar de la siguiente manera. Se coloca un marcador en el cero de la recta numérica y se lanza una moneda justa. Si cae en cara, el marcador se mueve una unidad hacia la derecha. Si cae cruz, el marcador se mueve una unidad hacia la izquierda. Después de cinco lanzamientos, el marcador ahora podría estar en -5, -3, -1, 1, 3, 5. Con cinco lanzamientos, tres caras y dos cruces, en cualquier orden, aterrizará en 1. Hay 10 formas de aterrizar en 1 (girando tres cabezas y dos colas), 10 formas de aterrizar en -1 (girando tres colas y dos cabezas), 5 formas de aterrizar en 3 (girando cuatro cabezas y una cola), 5 formas de aterrizar en -3 (girando cuatro colas y una cabeza), 1 forma de aterrizar en 5 (girando cinco cabezas) y 1 forma de aterrizar en -5 (girando cinco colas). Consulte la figura siguiente para ver una ilustración de los posibles resultados de 5 lanzamientos.

Todos los resultados posibles del paseo aleatorio después de 5 lanzamientos de una moneda justa

Paseo aleatorio en dos dimensiones (versión animada)

Paseo aleatorio en dos dimensiones con 25 mil pasos (versión animada)

Paseo aleatorio en dos dimensiones con dos millones de pasos aún más pequeños. Esta imagen se generó de tal manera que los puntos que se atraviesan con más frecuencia sean más oscuros. En el límite, para pasos muy pequeños, se obtiene el movimiento browniano .

Para definir este recorrido formalmente, tome variables aleatorias independientes , donde cada variable es 1 o −1, con una probabilidad del 50% para cualquier valor, y establezca y La serie se denomina recorrido aleatorio simple . Esta serie (la suma de la secuencia de −1 y 1) da la distancia neta recorrida, si cada parte de la caminata tiene una longitud uno. La expectativa de es cero. Es decir, la media de todos los lanzamientos de moneda se acerca a cero a medida que aumenta el número de lanzamientos. Esto se desprende de la propiedad de aditividad finita de la expectativa: ${\displaystyle Z_{1},Z_{2},\dots }$ ${\displaystyle S_{0}=0}$ ${\textstyle S_{n}=\sum _{j=1}^{n}Z_{j}.}$ ${\displaystyle \{S_{n}\}}$ ${\displaystyle \mathbb {Z} }$ ${\displaystyle E(S_{n})}$ ${\displaystyle S_{n}}$

$${\displaystyle E(S_{n})=\sum _{j=1}^{n}E(Z_{j})=0.}$$

Un cálculo similar, utilizando la independencia de las variables aleatorias y el hecho de que , muestra que: ${\displaystyle E(Z_{n}^{2})=1}$

$${\displaystyle E(S_{n}^{2})=\sum _{i=1}^{n}E(Z_{i}^{2})+2\sum _{1\leq i<j\leq n}E(Z_{i}Z_{j})=n.}$$

Esto sugiere que la distancia de traducción esperada después de n pasos debe ser del orden de . De hecho, ^[5] ${\displaystyle E(|S_{n}|)\,\!}$ ${\displaystyle {\sqrt {n}}}$

$${\displaystyle \lim _{n\to \infty }{\frac {E(|S_{n}|)}{\sqrt {n}}}={\sqrt {\frac {2}{\pi }}}.}$$

Para responder a la pregunta de cuántas veces un paseo aleatorio cruzará una línea límite si se le permite continuar caminando para siempre, un paseo aleatorio simple cruzará cada punto un número infinito de veces. Este resultado tiene muchos nombres: fenómeno del paso a nivel , recurrencia o ruina del jugador . El motivo del apellido es el siguiente: un jugador con una cantidad finita de dinero eventualmente perderá cuando juegue un juego limpio contra un banco con una cantidad infinita de dinero. El dinero del jugador realizará un recorrido aleatorio, llegará a cero en algún momento y el juego terminará. ${\displaystyle \mathbb {Z} }$

Si a y b son enteros positivos, entonces el número esperado de pasos hasta que un paseo aleatorio simple unidimensional que comienza en 0 llega por primera vez a b o − a es ab . La probabilidad de que este paseo llegue a b antes de −a es , lo que puede derivarse del hecho de que el paseo aleatorio simple es una martingala . Y estas expectativas y probabilidades de acierto se pueden calcular en la cadena de Markov de paseo aleatorio unidimensional general. ${\displaystyle a/(a+b)}$ ${\displaystyle O(a+b)}$

Algunos de los resultados mencionados anteriormente se pueden derivar de las propiedades del triángulo de Pascal . El número de recorridos diferentes de n pasos donde cada paso es +1 o −1 es 2 ⁿ . Para el paseo aleatorio simple, cada uno de estos paseos es igualmente probable. Para que S _n sea igual a un número k es necesario y suficiente que el número de +1 en el paseo supere en k a los de −1 . De ello se deduce que +1 debe aparecer ( n  +  k )/2 veces entre n pasos de una caminata, por lo tanto, el número de caminatas que satisfacen es igual al número de formas de elegir ( n  +  k )/2 elementos de un conjunto de n elementos, ^{[ 6]} denotado . Para que esto tenga significado, es necesario que n  +  k sea un número par, lo que implica que n y k son ambos pares o impares. Por tanto, la probabilidad de que sea igual a . Al representar las entradas del triángulo de Pascal en términos de factoriales y utilizar la fórmula de Stirling , se pueden obtener buenas estimaciones de estas probabilidades para valores grandes de . ${\displaystyle S_{n}=k}$ ${\textstyle n \choose (n+k)/2}$ ${\displaystyle S_{n}=k}$ ${\textstyle 2^{-n}{n \choose (n+k)/2}}$ ${\displaystyle n}$

Si el espacio se limita a + por brevedad, el número de formas en que una caminata aleatoria aterrizará en cualquier número dado que tenga cinco lanzamientos se puede mostrar como {0,5,0,4,0,1}. ${\displaystyle \mathbb {Z} }$

Esta relación con el triángulo de Pascal se demuestra para valores pequeños de n . En vueltas cero la única posibilidad será permanecer en cero. Sin embargo, en un turno, hay una posibilidad de aterrizar en -1 o una posibilidad de aterrizar en 1. En dos turnos, un marcador en 1 podría moverse a 2 o regresar a cero. Un marcador en −1 podría moverse a −2 o volver a cero. Por lo tanto, hay una posibilidad de aterrizar en -2, dos posibilidades de aterrizar en cero y una probabilidad de aterrizar en 2.

El teorema del límite central y la ley del logaritmo iterado describen aspectos importantes del comportamiento de los paseos aleatorios simples . En particular, lo primero implica que a medida que n aumenta, las probabilidades (proporcionales a los números en cada fila) se aproximan a una distribución normal . ${\displaystyle \mathbb {Z} }$

Como generalización directa, se pueden considerar paseos aleatorios en redes cristalinas (gráficos de cobertura abeliana de pliegues infinitos sobre gráficos finitos). En realidad, es posible establecer el teorema del límite central y el teorema de la gran desviación en este contexto. ^{[7] [8]}

Como cadena de Markov

Un paseo aleatorio unidimensional también puede considerarse como una cadena de Markov cuyo espacio de estados está dado por los números enteros . Para algún número p que satisfaga , las probabilidades de transición (la probabilidad Pi _,j de pasar del estado i al estado j ) están dadas. por ${\displaystyle i=0,\pm 1,\pm 2,\dots .}$ ${\displaystyle \,0<p<1}$

$${\displaystyle \,P_{i,i+1}=p=1-P_{i,i-1}.}$$

Generalización heterogénea

El paseo aleatorio heterogéneo extrae en cada paso de tiempo un número aleatorio que determina las probabilidades de salto locales y luego un número aleatorio que determina la dirección real del salto. La cuestión principal es la probabilidad de permanecer en cada uno de los distintos sitios después de los saltos, y en el límite de esta probabilidad cuando es muy grande. ${\displaystyle t}$ ${\displaystyle t}$

Dimensiones superiores

Tres paseos aleatorios en tres dimensiones

En dimensiones superiores, el conjunto de puntos recorridos aleatoriamente tiene propiedades geométricas interesantes. De hecho, se obtiene un fractal discreto , es decir, un conjunto que exhibe autosimilitud estocástica a grandes escalas. A pequeñas escalas, se pueden observar "irregularidades" resultantes de la retícula sobre la que se realiza la caminata. La trayectoria de una caminata aleatoria es el conjunto de puntos visitados, considerados como un conjunto sin tener en cuenta cuándo llegó la caminata al punto. En una dimensión, la trayectoria es simplemente todos los puntos entre la altura mínima y la altura máxima alcanzada por la caminata (ambos son, en promedio, del orden de ). ${\displaystyle {\sqrt {n}}}$

Para visualizar el caso bidimensional, uno puede imaginar a una persona caminando aleatoriamente por una ciudad. La ciudad es efectivamente infinita y está dispuesta en una cuadrícula de aceras. En cada intersección, la persona elige al azar una de las cuatro rutas posibles (incluida la que viajó originalmente). Formalmente, se trata de un paseo aleatorio sobre el conjunto de todos los puntos del plano con coordenadas enteras .

Para responder a la pregunta de si la persona alguna vez regresará al punto de partida original de la caminata, este es el equivalente bidimensional del problema del paso a nivel discutido anteriormente. En 1921 George Pólya demostró que la persona casi seguramente lo haría en un paseo aleatorio bidimensional, pero para 3 dimensiones o más, la probabilidad de regresar al origen disminuye a medida que aumenta el número de dimensiones. En 3 dimensiones, la probabilidad disminuye a aproximadamente el 34%. ^[9] Se sabía que el matemático Shizuo Kakutani se refería a este resultado con la siguiente cita: "Un hombre borracho encontrará el camino a casa, pero un pájaro borracho puede perderse para siempre". ^[10]

Otra variación de esta pregunta que también hizo Pólya es: "si dos personas salen del mismo punto de partida, ¿se volverán a encontrar?" ^[11] Se puede demostrar que la diferencia entre sus ubicaciones (dos paseos aleatorios independientes) también es un paseo aleatorio simple, por lo que es casi seguro que se reencuentran en un paseo bidimensional, pero para 3 dimensiones y más la probabilidad disminuye con la número de dimensiones. Paul Erdős y Samuel James Taylor también demostraron en 1960 que para dimensiones menores o iguales a 4, dos paseos aleatorios independientes que parten de dos puntos dados tienen casi con seguridad un número infinito de intersecciones, pero para dimensiones superiores a 5, es casi seguro que se cruzan sólo con una frecuencia finita. . ^[12]

La función asintótica para un paseo aleatorio bidimensional a medida que aumenta el número de pasos viene dada por una distribución de Rayleigh . La distribución de probabilidad es función del radio desde el origen y la longitud del paso es constante para cada paso. Aquí, se supone que la longitud del paso es 1, N es el número total de pasos y r es el radio desde el origen. ^[13]

$${\displaystyle P(r)={\frac {2r}{N}}e^{-r^{2}/N}}$$

Relación con el proceso de Wiener

Pasos simulados que se aproximan a un proceso Wiener en dos dimensiones.

Un proceso de Wiener es un proceso estocástico con un comportamiento similar al movimiento browniano , el fenómeno físico de una partícula diminuta que se difunde en un fluido. (A veces el proceso de Wiener se llama "movimiento browniano", aunque en sentido estricto se trata de una confusión entre un modelo y el fenómeno que se está modelando).

Un proceso de Wiener es el límite de escala del paseo aleatorio en la dimensión 1. Esto significa que si hay un paseo aleatorio con pasos muy pequeños, hay una aproximación a un proceso de Wiener (y, con menos precisión, al movimiento browniano). Para ser más precisos, si el tamaño del paso es ε, es necesario realizar una caminata de longitud L /ε ² para aproximar una longitud de Wiener de L . A medida que el tamaño del paso tiende a 0 (y el número de pasos aumenta proporcionalmente), el paseo aleatorio converge a un proceso de Wiener en un sentido apropiado. Formalmente, si B es el espacio de todos los caminos de longitud L con la topología máxima, y ​​si M es el espacio de medida sobre B con la topología norma, entonces la convergencia está en el espacio M. De manera similar, un proceso de Wiener en varias dimensiones es el límite de escala del paseo aleatorio en el mismo número de dimensiones.

Un paseo aleatorio es un fractal discreto (una función con dimensiones enteras; 1, 2, ...), pero la trayectoria del proceso de Wiener es un fractal verdadero y existe una conexión entre los dos. Por ejemplo, realice una caminata aleatoria hasta llegar a un círculo de radio r multiplicado por la longitud del paso. El número promedio de pasos que realiza es r ² . ^{[ cita necesaria ]} Este hecho es la versión discreta del hecho de que un recorrido por el proceso de Wiener es un fractal de la dimensión  2 de Hausdorff. ^{[ cita necesaria ]}

En dos dimensiones, el número promedio de puntos que tiene el mismo paseo aleatorio en el límite de su trayectoria es r ^4/3 . Esto corresponde al hecho de que el límite de la trayectoria de un proceso de Wiener es un fractal de dimensión 4/3, un hecho predicho por Mandelbrot mediante simulaciones pero demostrado sólo en 2000 por Lawler , Schramm y Werner . ^[14]

Un proceso de Wiener disfruta de muchas simetrías que un paseo aleatorio no tiene. Por ejemplo, el recorrido del proceso de Wiener es invariante para las rotaciones, pero el recorrido aleatorio no lo es, ya que la cuadrícula subyacente no lo es (el recorrido aleatorio es invariante para las rotaciones de 90 grados, pero los procesos de Wiener son invariantes para las rotaciones de, por ejemplo, 17 grados). también). Esto significa que, en muchos casos, los problemas de un paseo aleatorio son más fáciles de resolver traduciéndolos a un proceso de Wiener, resolviendo el problema allí y luego traduciéndolo nuevamente. Por otro lado, algunos problemas son más fáciles de resolver con paseos aleatorios debido a su naturaleza discreta.

La caminata aleatoria y el proceso de Wiener pueden acoplarse , es decir, manifestarse en el mismo espacio de probabilidad de una manera dependiente que los obliga a estar bastante cerca. El acoplamiento más simple es la incrustación de Skorokhod , pero existen acoplamientos más precisos, como el teorema de aproximación de Komlós-Major-Tusnády .

La convergencia de un paseo aleatorio hacia el proceso de Wiener está controlada por el teorema del límite central y por el teorema de Donsker . Para una partícula en una posición fija conocida en t  = 0, el teorema del límite central nos dice que después de un gran número de pasos independientes en el paseo aleatorio, la posición del caminante se distribuye según una distribución normal de varianza total :

$${\displaystyle \sigma ^{2}={\frac {t}{\delta t}}\,\varepsilon ^{2},}$$

donde t es el tiempo transcurrido desde el inicio del paseo aleatorio, es el tamaño de un paso del paseo aleatorio y es el tiempo transcurrido entre dos pasos sucesivos. ${\displaystyle \varepsilon }$ ${\displaystyle \delta t}$

Esto corresponde a la función de Green de la ecuación de difusión que controla el proceso de Wiener, lo que sugiere que, después de un gran número de pasos, el paseo aleatorio converge hacia un proceso de Wiener.

En 3D, la varianza correspondiente a la función de Green de la ecuación de difusión es:

$${\displaystyle \sigma ^{2}=6\,D\,t.}$$

Igualando esta cantidad con la varianza asociada a la posición del caminante aleatorio, se obtiene el coeficiente de difusión equivalente a considerar para el proceso asintótico de Wiener hacia el cual converge el paseo aleatorio después de un gran número de pasos:

$${\displaystyle D={\frac {\varepsilon ^{2}}{6\delta t}}}$$

Las dos expresiones de la varianza anteriores corresponden a la distribución asociada al vector que une los dos extremos del paseo aleatorio, en 3D. La varianza asociada a cada componente , o es solo un tercio de este valor (aún en 3D). ${\displaystyle {\vec {R}}}$ ${\displaystyle R_{x}}$ ${\displaystyle R_{y}}$ ${\displaystyle R_{z}}$

Para 2D: ^[15]

$${\displaystyle D={\frac {\varepsilon ^{2}}{4\delta t}}.}$$

Para 1D: ^[16]

$${\displaystyle D={\frac {\varepsilon ^{2}}{2\delta t}}.}$$

paseo aleatorio gaussiano

Un paseo aleatorio con un tamaño de paso que varía según una distribución normal se utiliza como modelo para datos de series temporales del mundo real, como los mercados financieros.

Aquí, el tamaño del paso es la distribución normal acumulativa inversa donde 0 ≤  z  ≤ 1 es un número aleatorio distribuido uniformemente, y μ y σ son las desviaciones media y estándar de la distribución normal, respectivamente. ${\displaystyle \Phi ^{-1}(z,\mu ,\sigma )}$

Si μ es distinto de cero, el paseo aleatorio variará aproximadamente en una tendencia lineal. Si v _s es el valor inicial del paseo aleatorio, el valor esperado después de n pasos será v _s + n μ.

Para el caso especial donde μ es igual a cero, después de n pasos, la distribución de probabilidad de la distancia de traslación viene dada por N (0, n σ ² ), donde N () es la notación de la distribución normal, n es el número de pasos , y σ proviene de la distribución normal acumulativa inversa como se indicó anteriormente.

Prueba: El paseo aleatorio gaussiano puede considerarse como la suma de una secuencia de variables aleatorias independientes e idénticamente distribuidas, X _i de la distribución normal acumulativa inversa con media igual a cero y σ de la distribución normal acumulativa inversa original:

${\displaystyle Z=\sum _{i=0}^{n}{X_{i}},}$

pero tenemos la distribución para la suma de dos variables aleatorias independientes distribuidas normalmente, Z = X + Y , está dada por

$${\displaystyle {\mathcal {N}}(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$$

(mira aquí)

En nuestro caso, μ _X = μ _Y = 0 y σ ² _X = σ ² _Y = σ ² producen

$${\displaystyle {\mathcal {N}}(0,2\sigma ^{2})}$$

ncuadrática media después de nla identidad de Bienaymé ${\displaystyle Z\sim {\mathcal {N}}(0,n\sigma ^{2}).}$

${\displaystyle {\sqrt {Var(S_{n})}}={\sqrt {E[S_{n}^{2}]}}=\sigma {\sqrt {n}}.}$

Pero para el paseo aleatorio gaussiano, esto es sólo la desviación estándar de la distribución de la distancia de traslación después de n pasos. Por lo tanto, si μ es igual a cero, y dado que la distancia de traducción cuadrática media (RMS) es una desviación estándar, existe un 68,27 % de probabilidad de que la distancia de traducción RMS después de n pasos caiga entre . Asimismo, existe un 50% de probabilidad de que la distancia de traslación después de n pasos esté entre . ${\displaystyle \pm \sigma {\sqrt {n}}}$ ${\displaystyle \pm 0.6745\sigma {\sqrt {n}}}$

Número de sitios distintos

El número de sitios distintos visitados por un solo caminante aleatorio se ha estudiado ampliamente para redes cuadradas y cúbicas y para fractales. ^{[17] [18]} Esta cantidad es útil para el análisis de problemas de atrapamiento y reacciones cinéticas. También está relacionado con la densidad vibratoria de los estados, ^{[19] [20],} los procesos de reacciones de difusión ^[21] y la dispersión de poblaciones en ecología. ^{[22] [23]} ${\displaystyle S(t)}$

Tarifa de información

La tasa de información de un paseo aleatorio gaussiano con respecto a la distancia de error al cuadrado, es decir, su función de distorsión de tasa cuadrática , viene dada paramétricamente por ^[24]

$${\displaystyle R(D_{\theta })={\frac {1}{2}}\int _{0}^{1}\max\{0,\log _{2}\left(S(\varphi )/\theta \right)\}\,d\varphi ,}$$

$${\displaystyle D_{\theta }=\int _{0}^{1}\min\{S(\varphi ),\theta \}\,d\varphi ,}$$

código binariobitscódigo binario ${\displaystyle S(\varphi )=\left(2\sin(\pi \varphi /2)\right)^{-2}}$ ${\displaystyle {\{Z_{n}\}_{n=1}^{N}}}$ ${\displaystyle NR(D_{\theta })}$ ${\displaystyle D_{\theta }}$ ${\displaystyle \varepsilon >0}$ ${\displaystyle N\in \mathbb {N} }$ ${\displaystyle 2^{NR(D_{\theta })}}$ ${\displaystyle {\{Z_{n}\}_{n=1}^{N}}}$ ${\displaystyle D_{\theta }-\varepsilon }$

Aplicaciones

La escultura Quantum Cloud de Antony Gormley en Londres fue diseñada por una computadora usando un algoritmo de caminata aleatoria

Como se mencionó, la variedad de fenómenos naturales que han sido objeto de intentos de descripción mediante algún tipo de paseos aleatorios es considerable, particularmente en física ^{[25] [26]} y química, ^[27] ciencia de materiales , ^{[28] [29]} y biología. . ^{[30] [31] [32]} Las siguientes son algunas aplicaciones específicas de paseos aleatorios:

• En economía financiera , la hipótesis del paseo aleatorio se utiliza para modelar los precios de las acciones y otros factores. ^[33] Los estudios empíricos encontraron algunas desviaciones de este modelo teórico, especialmente en las correlaciones a corto y largo plazo. Ver precios de acciones .
• En genética de poblaciones , el paseo aleatorio describe las propiedades estadísticas de la deriva genética.
• En física , los paseos aleatorios se utilizan como modelos simplificados de difusión y movimiento browniano físico, como el movimiento aleatorio de moléculas en líquidos y gases. Véase, por ejemplo, agregación limitada por difusión. También en física, los paseos aleatorios y algunos de los paseos autointeractivos desempeñan un papel en la teoría cuántica de campos .
• En la fabricación de semiconductores , se utilizan paseos aleatorios para analizar los efectos del tratamiento térmico en nodos más pequeños. Se aplica para comprender la difusión de dopantes , defectos , impurezas , etc., durante los pasos críticos de fabricación. Los tratamientos de caminata aleatoria también se utilizan para estudiar la difusión de reactivos, productos y plasma durante los procesos de deposición química de vapor . La difusión continua se ha utilizado para estudiar el flujo de gases, a escalas macroscópicas, en reactores CVD. Sin embargo, las dimensiones más pequeñas y la mayor complejidad nos han obligado a tratarlos con un paseo aleatorio. Esto permite un análisis preciso de los procesos estocásticos, a nivel molecular y más pequeño, en la fabricación de semiconductores.
• En ecología matemática , los paseos aleatorios se utilizan para describir movimientos de animales individuales, para respaldar empíricamente procesos de biodifusión y, ocasionalmente, para modelar la dinámica de poblaciones .
• En física de polímeros , el paseo aleatorio describe una cadena ideal . Es el modelo más sencillo para estudiar polímeros . ^[34]
• En otros campos de las matemáticas, el paseo aleatorio se utiliza para calcular soluciones de la ecuación de Laplace , para estimar la medida armónica y para diversas construcciones en análisis y combinatoria .
• En informática , los paseos aleatorios se utilizan para estimar el tamaño de la Web . ^[35]
• En la segmentación de imágenes , se utilizan recorridos aleatorios para determinar las etiquetas (es decir, "objeto" o "fondo") que se asociarán con cada píxel. ^[36] Este algoritmo suele denominarse algoritmo de segmentación de caminantes aleatorios .

• En la investigación del cerebro , se utilizan paseos aleatorios y paseos aleatorios reforzados para modelar cascadas de activación neuronal en el cerebro.
• En la ciencia de la visión , la deriva ocular tiende a comportarse como un paseo aleatorio. ^[37] Según algunos autores, los movimientos oculares de fijación en general también se describen bien mediante una caminata aleatoria. ^[38]
• En psicología , los paseos aleatorios explican con precisión la relación entre el tiempo necesario para tomar una decisión y la probabilidad de que se tome una determinada decisión. ^[39]
• Los paseos aleatorios se pueden utilizar para tomar muestras de un espacio de estados desconocido o muy grande, por ejemplo, para seleccionar una página aleatoria de Internet. ^{[ cita necesaria ]} En informática , este método se conoce como Markov Chain Monte Carlo (MCMC).

• En las redes inalámbricas , se utiliza un paseo aleatorio para modelar el movimiento de los nodos. ^{[ cita necesaria ]}
• Las bacterias móviles realizan paseos aleatorios sesgados . ^[40]
• En física, los paseos aleatorios son la base del método de estimación de Fermi . ^{[ cita necesaria ]}
• En la web, el sitio web de Twitter utiliza paseos aleatorios para hacer sugerencias sobre a quién seguir ^[41]
• Dave Bayer y Persi Diaconis han demostrado que 7 barajas son suficientes para mezclar una baraja de cartas (ver más detalles en barajar ). Este resultado se traduce en una afirmación sobre el paseo aleatorio en el grupo simétrico , que es lo que demuestran, con un uso crucial de la estructura del grupo mediante el análisis de Fourier.

Variantes

Se han considerado varios tipos de procesos estocásticos que son similares a los paseos aleatorios puros, pero en los que se permite que la estructura simple sea más generalizada. La estructura pura se puede caracterizar porque los pasos están definidos por variables aleatorias independientes e idénticamente distribuidas . Los paseos aleatorios pueden tener lugar en una variedad de espacios, como gráficos , números enteros, la línea real, el plano o espacios vectoriales de dimensiones superiores, en superficies curvas o variedades riemannianas de dimensiones superiores y en grupos . También es posible definir paseos aleatorios que dan sus pasos en momentos aleatorios, y en ese caso, la posición X
_ttiene que definirse para todos los tiempos t ∈ [0, +∞) . Los casos específicos o límites de paseos aleatorios incluyen el vuelo de Lévy y los modelos de difusión como el movimiento browniano .

En gráficos

Un paseo aleatorio de longitud k en un gráfico G posiblemente infinito con raíz 0 es un proceso estocástico con variables aleatorias tales que y es un vértice elegido uniformemente al azar entre los vecinos de . Entonces el número es la probabilidad de que un paseo aleatorio de longitud k comience en v y termine en w . En particular, si G es un gráfico con raíz 0 , es la probabilidad de que un paseo aleatorio de un paso regrese a 0 . ${\displaystyle X_{1},X_{2},\dots ,X_{k}}$ ${\displaystyle X_{1}=0}$ ${\displaystyle {X_{i+1}}}$ ${\displaystyle X_{i}}$ ${\displaystyle p_{v,w,k}(G)}$ ${\displaystyle p_{0,0,2k}}$ ${\displaystyle 2k}$

Basándonos en la analogía de la sección anterior sobre dimensiones superiores, supongamos ahora que nuestra ciudad ya no es una cuadrícula perfecta. Cuando nuestra persona llega a un determinado cruce, elige con la misma probabilidad entre las distintas carreteras disponibles. Por tanto, si el cruce tiene siete salidas, la persona irá a cada una con una probabilidad de una séptima parte. Este es un paseo aleatorio en un gráfico. ¿Nuestra persona llegará a su casa? Resulta que, en condiciones bastante leves, la respuesta sigue siendo sí, ^[42] pero, según el gráfico, la respuesta a la pregunta variante "¿Se volverán a encontrar dos personas?" Puede que no sea que se encuentren infinitamente a menudo, casi con seguridad. ^[43]

Un ejemplo de un caso en el que la persona llegará casi con seguridad a su casa es cuando las longitudes de todos los bloques están entre a y b (donde a y b son dos números positivos finitos cualesquiera). Observe que no asumimos que el gráfico sea plano , es decir, que la ciudad pueda contener túneles y puentes. Una forma de comprobar este resultado es mediante la conexión a redes eléctricas . Toma un mapa de la ciudad y coloca una resistencia de un ohmio en cada bloque. Ahora mida la "resistencia entre un punto y el infinito". En otras palabras, elija algún número R y tome todos los puntos de la red eléctrica con una distancia mayor que R desde nuestro punto y conéctelos. Esta es ahora una red eléctrica finita y podemos medir la resistencia desde nuestro punto hasta los puntos cableados. Lleva R al infinito. El límite se llama resistencia entre un punto y el infinito . Resulta que lo siguiente es cierto (se puede encontrar una prueba elemental en el libro de Doyle y Snell):

Teorema : una gráfica es transitoria si y sólo si la resistencia entre un punto y el infinito es finita. No importa qué punto se elija si la gráfica es conexa.

En otras palabras, en un sistema transitorio, sólo se necesita superar una resistencia finita para llegar al infinito desde cualquier punto. En un sistema recurrente, la resistencia desde cualquier punto hasta el infinito es infinita.

Esta caracterización de fugacidad y recurrencia es muy útil, y concretamente nos permite analizar el caso de una ciudad dibujada en el plano con las distancias acotadas.

Un paseo aleatorio sobre un gráfico es un caso muy especial de cadena de Markov . A diferencia de una cadena de Markov general, el paseo aleatorio sobre un gráfico goza de una propiedad llamada simetría temporal o reversibilidad . A grandes rasgos, esta propiedad, también llamada principio de equilibrio detallado , significa que las probabilidades de recorrer un camino determinado en una dirección u otra tienen una conexión muy simple entre ellas (si la gráfica es regular , son simplemente iguales). Esta propiedad tiene consecuencias importantes.

A partir de la década de 1980, se han realizado muchas investigaciones para conectar las propiedades del gráfico con los paseos aleatorios. Además de la conexión de la red eléctrica descrita anteriormente, existen conexiones importantes con desigualdades isoperimétricas , ver más aquí , desigualdades funcionales como las desigualdades de Sobolev y Poincaré y propiedades de soluciones de la ecuación de Laplace . Una parte importante de esta investigación se centró en los gráficos de Cayley de grupos generados de forma finita . En muchos casos, estos resultados discretos se trasladan o se derivan de variedades y grupos de Lie .

En el contexto de los gráficos aleatorios , particularmente el del modelo Erdős-Rényi , se han obtenido resultados analíticos de algunas propiedades de los caminantes aleatorios. Estos incluyen la distribución del primer ^[44] y último tiempo de impacto ^[45] del caminante, donde el primer tiempo de impacto está dado por la primera vez que el caminante ingresa a un sitio previamente visitado del gráfico, y el último tiempo de impacto corresponde a la La primera vez, el caminante no puede realizar un movimiento adicional sin volver a visitar un sitio visitado anteriormente.

Una buena referencia para el paseo aleatorio sobre gráficos es el libro en línea de Aldous y Fill. Para grupos ver el libro de Woess. Si el núcleo de transición es en sí mismo aleatorio (basado en un entorno ), entonces el paseo aleatorio se denomina "camino aleatorio en un entorno aleatorio". Cuando la ley del paseo aleatorio incluye la aleatoriedad de , la ley se denomina ley de recocido; en cambio, si se considera fija, la ley se llama ley apagada. Véase el libro de Hughes, el libro de Revesz o las notas de conferencias de Zeitouni. ${\displaystyle p(x,y)}$ ${\displaystyle \omega }$ ${\displaystyle \omega }$ ${\displaystyle \omega }$

Podemos pensar en elegir cada ventaja posible con la misma probabilidad que maximizar la incertidumbre (entropía) localmente. También podríamos hacerlo globalmente: en el paseo aleatorio de máxima entropía (MERW) queremos que todos los caminos sean igualmente probables, o en otras palabras: por cada dos vértices, cada camino de longitud dada es igualmente probable. ^[46] Este paseo aleatorio tiene propiedades de localización mucho más fuertes.

Paseos aleatorios autointeractivos

Hay varios modelos interesantes de caminos aleatorios en los que cada paso depende del pasado de manera complicada. Todos son más complejos para resolver analíticamente que el paseo aleatorio habitual; Aún así, el comportamiento de cualquier modelo de caminante aleatorio se puede obtener mediante computadoras. Ejemplos incluyen:

• El camino que evita a uno mismo . ^[47]

El camino que se evita a sí mismo y de longitud n on es el camino aleatorio de n pasos que comienza en el origen, hace transiciones sólo entre sitios adyacentes en , nunca vuelve a visitar un sitio y se elige uniformemente entre todos esos caminos. En dos dimensiones, debido al autoatrapamiento, una caminata típica para evitarse es muy corta, ^[48] mientras que en una dimensión superior crece más allá de todos los límites. Este modelo se ha utilizado a menudo en la física de polímeros (desde la década de 1960). ${\displaystyle \mathbb {Z} ^{d}}$ ${\displaystyle \mathbb {Z} ^{d}}$

• "El paseo aleatorio borrado en bucle ". ^{[49] [50]}
• El paseo aleatorio reforzado. ^[51]
• El proceso de exploración. ^{[ cita necesaria ]}
• El paseo aleatorio multiagente. ^[52]

Paseos aleatorios sesgados en gráficos

Paseo aleatorio de entropía máxima

La caminata aleatoria elegida para maximizar la tasa de entropía tiene propiedades de localización mucho más fuertes.

Paseos aleatorios correlacionados

Paseos aleatorios en los que la dirección del movimiento en un momento dado se correlaciona con la dirección del movimiento en el momento siguiente. Se utiliza para modelar movimientos de animales. ^{[53] [54]}

Ver también

• Paseo aleatorio ramificado
• movimiento browniano
• Ley del logaritmo iterado
• Vuelo de Levy
• Hipótesis de búsqueda de alimento en vuelo de Lévy
• Paseo aleatorio borrado en bucle
• Paseo aleatorio de entropía máxima
• Caminata que evita a uno mismo
• raíz unitaria

Referencias

1. Pearson, Karl (1905). "El problema del paseo aleatorio". Naturaleza . 72 (1865): 294. Bibcode : 1905Natur..72..294P. doi :10.1038/072294b0. S2CID  4010776.
2. Teoría y aplicaciones de las simulaciones de Montecarlo. (2013). Croacia: IntechOpen. Página 229, https://books.google.de/books?id=3HWfDwAAQBAJ&pg=PA229
3. Pal, Révész (1990) Paseo aleatorio en entornos aleatorios y no aleatorios , World Scientific
4. Kohls, Moritz; Hernández, Tanja (2016). "Cobertura esperada del algoritmo de movilidad de caminata aleatoria". arXiv : 1611.02861 [estad.AP].
5. "Caminata aleatoria unidimensional - de Wolfram MathWorld". Mathworld.wolfram.com. 26 de abril de 2000 . Consultado el 2 de noviembre de 2016 .
6. Edward A. Codling et al., Modelos de paseo aleatorio en biología, Journal of the Royal Society Interface, 2008
7. Kotani, M.; Sunada, T. (2003). Geometría espectral de redes cristalinas . Matemáticas Contemporáneas. vol. 338, págs. 271–305. doi : 10.1090/conm/338/06077 . ISBN 978-0-8218-3383-4.
8. Kotani, M.; Sunada, T. (2006). "Gran desviación y cono tangente al infinito de una red cristalina". Matemáticas. Z.​ 254 (4): 837–870. doi :10.1007/s00209-006-0951-9. S2CID  122531716.
9. "Constantes de caminata aleatoria de Pólya". Mathworld.wolfram.com . Consultado el 2 de noviembre de 2016 .
10. Durrett, Rick (2010). Probabilidad: teoría y ejemplos . Prensa de la Universidad de Cambridge. págs.191. ISBN 978-1-139-49113-6.
11. Polya, George (1984). Probabilidad; combinatoria; Enseñanza y aprendizaje en matemáticas . Rota, Gian-Carlo, 1932-1999., Reynolds, MC, Shortt, Rae Michael. Cambridge, Massachusetts: MIT Press. págs. 582–585. ISBN 0-262-16097-8. OCLC  10208449.
12. Erdős, P.; Taylor, SJ (1960). "Algunas propiedades de intersección de caminos aleatorios". Acta Mathematica Academiae Scientiarum Hungaricae . 11 (3–4): 231–248. CiteSeerX 10.1.1.210.6357 . doi :10.1007/BF02020942. ISSN  0001-5954. S2CID  14143214. 
13. https://ocw.mit.edu/courses/18-366-random-walks-and-diffusion-fall-2006/aef0a2690183294e59ea8cb29f8dd448_lec01.pdf
14. MacKenzie, D. (2000). "MATEMÁTICAS: Tomando la medida de la danza más salvaje del mundo". Ciencia . 290 (5498): 1883–4. doi : 10.1126/ciencia.290.5498.1883. PMID  17742050. S2CID  12829171. (Errata:  doi :10.1126/science.291.5504.597)
15. Capítulo 2 DIFUSIÓN. dartmouth.edu.
16. Ecuación de difusión para el paseo aleatorio Archivado el 21 de abril de 2015 en Wayback Machine . física.uakron.edu.
17. Weiss, George H.; Rubin, Robert J. (1982). "Paseos aleatorios: teoría y aplicaciones seleccionadas". Avances en Física Química . vol. 52, págs. 363–505. doi :10.1002/9780470142769.ch5. ISBN 978-0-470-14276-9.
18. Blumen, A.; Klafter, J.; Zumofen, G. (1986). "Modelos de dinámica de reacción en gafas". Espectroscopia óptica de gafas . Física y Química de Materiales con Estructuras de Bajas Dimensiones. vol. 1. págs. 199–265. Código Bib : 1986PCMLD...1..199B. doi :10.1007/978-94-009-4650-7_5. ISBN 978-94-010-8566-3.
19. Alejandro, S.; Orbach, R. (1982). «Densidad de estados sobre fractales: "fractones"» (PDF) . Revista de Physique Lettres . 43 (17): 625–631. doi :10.1051/jphyslet:019820043017062500. S2CID  67757791.
20. Rammal, R.; Toulouse, G. (1983). "Paseos aleatorios sobre estructuras fractales y grupos de percolación". Revista de Physique Lettres . 44 (1): 13–22. doi :10.1051/jphyslet:0198300440101300.
21. Smoluchowski, MV (1917). "Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen". Z. Phys. Química. (29): 129-168., Rice, SA (1 de marzo de 1985). Reacciones de difusión limitada. Cinética Química Integral. vol. 25. Elsevier. ISBN 978-0-444-42354-2. Consultado el 13 de agosto de 2013 .
22. Skellam, JG (1951). "Dispersión aleatoria en poblaciones teóricas". Biometrika . 38 (1/2): 196–218. doi :10.2307/2332328. JSTOR  2332328. PMID  14848123.
23. Skellam, JG (1952). "Estudios en Ecología Estadística: I. Patrón espacial". Biometrika . 39 (3/4): 346–362. doi :10.2307/2334030. JSTOR  2334030.
24. Berger, T. (1970). "Tasas de información de los procesos Wiener". Transacciones IEEE sobre teoría de la información . 16 (2): 134-139. doi :10.1109/TIT.1970.1054423.
25. Risken H. (1984) La ecuación de Fokker-Planck . Springer, Berlín.
26. De Gennes PG (1979) Conceptos de escala en física de polímeros . Cornell University Press, Ithaca y Londres.
27. Van Kampen NG (1992) Procesos estocásticos en física y química , edición revisada y ampliada. Holanda Septentrional, Ámsterdam.
28. Weiss, George H. (1994). Aspectos y Aplicaciones del Random Walk . Materiales y procesos aleatorios. North-Holland Publishing Co., Ámsterdam. ISBN 978-0-444-81606-1. SEÑOR  1280031.
29. Doi M. y Edwards SF (1986) La teoría de la dinámica de los polímeros . Prensa de Clarendon, Oxford
30. Goel NW y Richter-Dyn N. (1974) Modelos estocásticos en biología . Prensa académica, Nueva York.
31. Redner S. (2001) Una guía para el proceso de primer paso . Cambridge University Press, Cambridge, Reino Unido.
32. Cox DR (1962) Teoría de la renovación . Methuen, Londres.
33. David A. Kodde y Hein Schreuder (1984), Previsión de ingresos y beneficios corporativos: modelos de series de tiempo frente a gestión y analistas, Journal of Business Finance and Accounting, vol. 11, nº 3, otoño de 1984
34. Jones, RAL (2004). Materia condensada blanda (Reimpresión. Ed.). Oxford [ua]: Universidad de Oxford. Pr. págs. 77–78. ISBN 978-0-19-850589-1.
35. Bar-Yossef, Ziv; Gurevich, Maxim (2008). "Muestreo aleatorio del índice de un motor de búsqueda". Revista de la ACM . Asociación de Maquinaria de Computación (ACM). 55 (5): 1–74. doi :10.1145/1411509.1411514. ISSN  0004-5411.
36. Grady, L (2006). "Paseos aleatorios para segmentación de imágenes" (PDF) . Transacciones IEEE sobre análisis de patrones e inteligencia artificial . 28 (11): 1768–83. CiteSeerX 10.1.1.375.3389 . doi :10.1109/TPAMI.2006.233. PMID  17063682. S2CID  489789. Archivado desde el original (PDF) el 5 de julio de 2017 . Consultado el 2 de noviembre de 2016 . 
37. Rucci, M; Víctor, JD (2015). "El ojo inestable: una etapa de procesamiento de información, no un error". Tendencias en Neurociencias . 38 (4): 195–206. doi :10.1016/j.tins.2015.01.005. PMC 4385455 . PMID  25698649. 
38. Engbert, R.; Mergenthaler, K.; Sinn, P.; Pikovsky, A. (2011). "Un modelo integrado de microsacadas y movimientos oculares de fijación". Procedimientos de la Academia Nacional de Ciencias . 108 (39): E765-70. Código Bib : 2011PNAS..108E.765E. doi : 10.1073/pnas.1102730108 . PMC 3182695 . PMID  21873243. 
39. Nosofsky, RM; Palmeri, TJ (1997). "Un modelo de paseo aleatorio de clasificación acelerada basado en ejemplos" (PDF) . Revisión psicológica . 104 (2): 266–300. doi :10.1037/0033-295x.104.2.266. PMID  9127583. Archivado desde el original (PDF) el 10 de diciembre de 2004.
40. Codling, EA; Plancha, MJ; Benhamou, S. (6 de agosto de 2008). "Modelos de paseo aleatorio en biología". Revista de la interfaz de la Royal Society . 5 (25): 813–834. doi :10.1098/rsif.2008.0014. PMC 2504494 . PMID  18426776. 
41. Gupta, Pankaj y col. WTF: El sistema a quién seguir en Twitter, Actas de la 22ª conferencia internacional sobre la World Wide Web
42. Es interesante observar que en un gráfico general el encuentro de dos caminantes aleatorios independientes no siempre se reduce al problema de que un solo paseo aleatorio regrese a su punto de partida.
43. Krishnapur, Manjunath; Peres, Yuval (2004). "Gráficos recurrentes donde dos paseos aleatorios independientes chocan con una frecuencia finita". Comunicaciones electrónicas en probabilidad . 9 : 72–81. arXiv : matemáticas/0406487 . Código Bib : 2004 matemáticas ...... 6487K. doi :10.1214/ECP.v9-1111. ISSN  1083-589X. S2CID  16584737.
44. Tishby, ido; Biham, Ofer; Katzav, Eytan (2017). "La distribución de los primeros tiempos de acceso de los paseos aleatorios en las redes Erdős-Rényi". Revista de Física A: Matemática y Teórica . 50 (11): 115001. arXiv : 1606.01560 . Código Bib : 2017JPhA...50k5001T. doi :10.1088/1751-8121/aa5af3. S2CID  118850609.
45. Tishby, ido; Biham, Ofer; Katzav, Eytan (2016). "La distribución de la longitud de los caminos que evitan los paseos por cuenta propia en las redes Erdős-Rényi". Revista de Física A: Matemática y Teórica . 49 (28): 285002. arXiv : 1603.06613 . Código Bib : 2016JPhA...49B5002T. doi :10.1088/1751-8113/49/28/285002. S2CID  119182848.
46. Burda, Z.; Duda, J.; Suerte, JM; Waclaw, B. (2009). "Localización del paseo aleatorio de máxima entropía". Cartas de revisión física . 102 (16): 160602. arXiv : 0810.4113 . Código bibliográfico : 2009PhRvL.102p0602B. doi :10.1103/PhysRevLett.102.160602. PMID  19518691. S2CID  32134048.
47. Madras, Neal y Slade, Gordon (1996) La caminata que evita a uno mismo , Birkhäuser Boston. ISBN 0-8176-3891-1 . 
48. Hemmer, S.; Hemmer, ordenador personal (1984). "Un paseo aleatorio promedio que se evita a sí mismo sobre la celosía cuadrada dura 71 pasos". J. química. Física . 81 (1): 584–585. Código Bib :1984JChPh..81..584H. doi : 10.1063/1.447349 .
49. Lawler, Gregorio (1996). Intersección de paseos aleatorios , Birkhäuser Boston. ISBN 0-8176-3892-X . 
50. Lawler, Gregory Procesos conformemente invariantes en el plano , book.ps.
51. Pemantle, Robin (2007). "Un estudio de procesos aleatorios con refuerzo" (PDF) . Encuestas de probabilidad . 4 : 1–79. arXiv : matemáticas/0610076 . doi :10.1214/07-PS094. S2CID  11964062.
52. Alamgir, M. y von Luxburg, U. (2010). "Paseos aleatorios de múltiples agentes para agrupación local en gráficos" Archivado el 15 de abril de 2012 en Wayback Machine , Décima Conferencia Internacional sobre Minería de Datos (ICDM) del IEEE , págs.
53. Bovet, Pierre; Benhamou, Simón (1988). "Análisis espacial de los movimientos de los animales utilizando un modelo de paseo aleatorio correlacionado". Revista de Biología Teórica . 131 (4): 419–433. Código Bib : 1988JThBi.131..419B. doi :10.1016/S0022-5193(88)80038-9.
54. Kareiva, primer ministro; Shigesada, N. (1983). "Analizar el movimiento de los insectos como un paseo aleatorio correlacionado". Ecología . 56 (2–3): 234–238. Código bibliográfico : 1983Oecol..56..234K. doi :10.1007/BF00379695. PMID  28310199. S2CID  20329045.

Bibliografía

• Aldous, David ; Llenar, James Allen (2002). Cadenas de Markov reversibles y paseos aleatorios sobre gráficos. Archivado desde el original el 27 de febrero de 2019.
• Doyle, Peter G.; Snell, J. Laurie (1984). Paseos Aleatorios y Redes Eléctricas . Monografías matemáticas de Carus. vol. 22. Asociación Matemática de América . arXiv : math.PR/0001057 . ISBN 978-0-88385-024-4. SEÑOR  0920811.
• Feller, William (1968), Introducción a la teoría de la probabilidad y sus aplicaciones (volumen 1). ISBN 0-471-25708-7 
• Hughes, Barry D. (1996), Paseos aleatorios y entornos aleatorios , Oxford University Press. ISBN 0-19-853789-1 
• Norris, James (1998), Cadenas de Markov , Cambridge University Press. ISBN 0-521-63396-6 
• Pólya G.(1921), "Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Strassennetz" Archivado el 4 de marzo de 2016 en Wayback Machine , Mathematische Annalen , 84(1–2):149–160, marzo de 1921.
• Révész, Pal (2013), Paseo aleatorio en entornos aleatorios y no aleatorios (tercera edición) , World Scientific Pub Co. ISBN 978-981-4447-50-8 
• Sunada, Toshikazu (2012). Cristalografía topológica: con miras al análisis geométrico discreto . Encuestas y Tutorías en Ciencias Matemáticas Aplicadas. vol. 6. Saltador. ISBN 978-4-431-54177-6.
• Weiss G. Aspectos y aplicaciones del Random Walk , Holanda Septentrional, 1994.
• Woess, Wolfgang (2000), Paseos aleatorios sobre grupos y gráficos infinitos , tratados de matemáticas de Cambridge 138, Cambridge University Press. ISBN 0-521-55292-3 

enlaces externos

• Constantes de caminata aleatoria de Pólya
• Paseo aleatorio en el subprograma de Java Archivado el 31 de agosto de 2007 en Wayback Machine.
• Paseo aleatorio cuántico
• Estimador de paseo aleatorio gaussiano
• Modelos de conductancia electrónica que utilizan paseos aleatorios de entropía máxima Proyecto de demostraciones de Wolfram