Un vuelo de Lévy es una caminata aleatoria en la que las longitudes de los pasos tienen una distribución estable , [1] una distribución de probabilidad de cola pesada . Cuando se define como un paseo en un espacio de dimensión mayor que uno, los pasos realizados son en direcciones aleatorias isotrópicas . Investigadores posteriores han ampliado el uso del término "vuelo de Lévy" para incluir también casos en los que el paseo aleatorio tiene lugar en una cuadrícula discreta en lugar de en un espacio continuo. [2]
El término "vuelo de Lévy" fue acuñado en honor a Paul Lévy por Benoît Mandelbrot , [3] quien lo utilizó para una definición específica de la distribución de los tamaños de paso. Usó el término vuelo de Cauchy para el caso en que la distribución de tamaños de paso es una distribución de Cauchy , [4] y vuelo de Rayleigh para cuando la distribución es una distribución normal [5] (que no es un ejemplo de una distribución de probabilidad de cola pesada). ).
El caso particular para el cual Mandelbrot utilizó el término "vuelo de Lévy" [3] se define por la función de supervivencia de la distribución de tamaños de pasos, U , siendo [6]
Aquí D es un parámetro relacionado con la dimensión fractal y la distribución es un caso particular de la distribución de Pareto .
Los vuelos de Lévy son, por construcción, procesos de Markov . Para distribuciones generales del tamaño de paso, que satisfacen la condición de potencia, la distancia desde el origen del recorrido aleatorio tiende, después de un gran número de pasos, a una distribución estable debido al teorema del límite central generalizado , lo que permite que muchos procesos modelarse utilizando vuelos de Lévy.
Las densidades de probabilidad de las partículas que experimentan un vuelo de Levy se pueden modelar utilizando una versión generalizada de la ecuación de Fokker-Planck , que suele utilizarse para modelar el movimiento browniano . La ecuación requiere el uso de derivadas fraccionarias . Para longitudes de salto que tienen una distribución de probabilidad simétrica, la ecuación toma una forma simple en términos de la derivada fraccionaria de Riesz . En una dimensión, la ecuación se lee como
donde γ es una constante similar a la constante de difusión, α es el parámetro de estabilidad [ cita necesaria ] y f ( x , t ) es el potencial. La derivada de Riesz puede entenderse en términos de su Transformada de Fourier .
Esto se puede ampliar fácilmente a múltiples dimensiones.
Otra propiedad importante del vuelo de Lévy es la de varianzas divergentes en todos los casos excepto en el de α = 2, es decir, el movimiento browniano. En general, el momento fraccional θ de la distribución diverge si α ≤ θ . También,
La escala exponencial de las longitudes de los pasos le da a los vuelos de Lévy una propiedad invariante de escala , [ cita necesaria ] y se utilizan para modelar datos que exhiben agrupamiento. [ cita necesaria ]
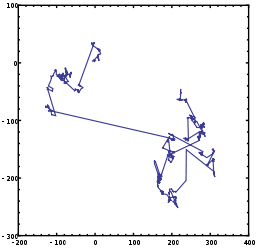
La definición de vuelo de Lévy proviene de las matemáticas relacionadas con la teoría del caos y es útil en mediciones estocásticas y simulaciones de fenómenos naturales aleatorios o pseudoaleatorios. Los ejemplos incluyen análisis de datos de terremotos , matemáticas financieras , criptografía , análisis de señales, así como muchas aplicaciones en astronomía , biología y física .
Se ha descubierto que el salto entre estados climáticos observados en el registro paleoclimático puede describirse como un vuelo de Lévy o un proceso alfa-estable [7] Otra aplicación es la hipótesis de búsqueda de alimento del vuelo de Lévy . Cuando los tiburones y otros depredadores del océano no pueden encontrar alimento, abandonan el movimiento browniano , el movimiento aleatorio que se observa en las moléculas de gas arremolinadas, por el vuelo de Lévy, una mezcla de trayectorias largas y movimientos cortos y aleatorios que se encuentran en fluidos turbulentos. Los investigadores analizaron más de 12 millones de movimientos registrados durante 5.700 días en 55 animales etiquetados con registradores de datos de 14 especies de depredadores oceánicos en los océanos Atlántico y Pacífico, incluidos tiburones sedosos , atún de aleta amarilla , aguja azul y pez espada. Los datos mostraron que los vuelos de Lévy intercalados con movimientos brownianos pueden describir los patrones de caza de los animales. [8] [9] [10] [11] Las aves y otros animales (incluidos los humanos) [12] siguen rutas que han sido modeladas utilizando el vuelo de Lévy (por ejemplo, cuando buscan comida). [13] Un ejemplo de un animal, específicamente un escarabajo, que utiliza los patrones de vuelo de Lévy es Pterostichus melanarius . Cuando los escarabajos tienen hambre y la comida escasea, evitan buscar presas en lugares que han visitado otros individuos de P. melanarius . Este comportamiento es óptimo para presas muy dispersas que no siempre se consumen por completo al mismo tiempo, como las babosas. [14]
Además, el vuelo biológico aparentemente también puede ser imitado por otros modelos, como los paseos aleatorios correlacionados compuestos, que crecen a través de escalas para converger en paseos óptimos de Lévy. [13] Las caminatas brownianas compuestas pueden ajustarse con precisión a las caminatas de Lévy teóricamente óptimas, pero no son tan eficientes como la búsqueda de Lévy en la mayoría de los tipos de paisajes, lo que sugiere que la presión de selección para las características de las caminatas de Lévy es más probable que los patrones difusos normales de múltiples escalas. [15]
Se puede realizar un enrutamiento eficiente en una red mediante enlaces que tengan una distribución de longitud de vuelo de Levy con valores específicos de alfa. [2]
![{\displaystyle F_{k}\left[{\frac {\partial ^{\alpha }\varphi (x,t)}{\partial |x|^{\alpha }}}\right]=-|k| ^{\alpha }F_{k}[\varphi (x,t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2991424fe3f2d2284bd5e8c81d1a70845503c83)
