En matemáticas y lógica matemática , el álgebra booleana es una rama del álgebra . Se diferencia del álgebra elemental en dos aspectos. Primero, los valores de las variables son los valores de verdad verdadero y falso , normalmente denotados 1 y 0, mientras que en álgebra elemental los valores de las variables son números. En segundo lugar, el álgebra booleana utiliza operadores lógicos como la conjunción ( y ) denotada como ∧ , la disyunción ( o ) denotada como ∨ y la negación ( no ) denotada como ¬ . El álgebra elemental, por otro lado, utiliza operadores aritméticos como la suma, la multiplicación, la resta y la división. El álgebra de Boole es, por tanto, una forma formal de describir operaciones lógicas , de la misma manera que el álgebra elemental describe operaciones numéricas.
El álgebra booleana fue introducida por George Boole en su primer libro, The Mathematical Analysis of Logic [1] (1847), y expuesta más detalladamente en su An Investigation of the Laws of Thought (1854). [2] Según Huntington , el término "álgebra booleana" fue sugerido por primera vez por Henry M. Sheffer en 1913, [3] aunque Charles Sanders Peirce dio el título "Un álgebra booleana [ sic ] con una constante" al primer capítulo de su "Las matemáticas más simples" en 1880. [4] El álgebra de Boole ha sido fundamental en el desarrollo de la electrónica digital y está incluida en todos los lenguajes de programación modernos . También se utiliza en teoría de conjuntos y estadística . [5]
Un precursor del álgebra de Boole fue el álgebra de conceptos de Gottfried Wilhelm Leibniz . El uso del binario en relación con el I Ching fue fundamental para la caracteristica universalis de Leibniz . Con el tiempo creó las bases del álgebra de conceptos. [6] El álgebra de conceptos de Leibniz es deductivamente equivalente al álgebra de conjuntos de Boole. [7]
El álgebra de Boole es anterior a los desarrollos modernos del álgebra abstracta y la lógica matemática ; sin embargo, se considera relacionado con los orígenes de ambos campos. [8] En un entorno abstracto, el álgebra booleana fue perfeccionada a finales del siglo XIX por Jevons , Schröder , Huntington y otros, hasta alcanzar la concepción moderna de una estructura matemática (abstracta) . [8] Por ejemplo, la observación empírica de que se pueden manipular expresiones en el álgebra de conjuntos , traduciéndolas a expresiones en el álgebra de Boole, se explica en términos modernos diciendo que el álgebra de conjuntos es un álgebra de Boole (obsérvese el artículo indefinido ). De hecho, MH Stone demostró en 1936 que todo álgebra de Boole es isomorfa a un cuerpo de conjuntos .
En la década de 1930, mientras estudiaba los circuitos de conmutación , Claude Shannon observó que también se podían aplicar las reglas del álgebra de Boole en este contexto, [9] e introdujo el álgebra de conmutación como una forma de analizar y diseñar circuitos por medios algebraicos en términos de puertas lógicas. . Shannon ya tenía a su disposición el aparato matemático abstracto, por lo que presentó su álgebra de conmutación como el álgebra booleana de dos elementos . En los entornos modernos de ingeniería de circuitos, hay poca necesidad de considerar otras álgebras booleanas, por lo que "álgebra de conmutación" y "álgebra booleana" se usan a menudo indistintamente. [10] [11] [12]
La implementación eficiente de funciones booleanas es un problema fundamental en el diseño de circuitos lógicos combinacionales . Las herramientas modernas de automatización de diseño electrónico para circuitos de integración a muy gran escala (VLSI) a menudo se basan en una representación eficiente de funciones booleanas conocidas como diagramas de decisión binaria (BDD) (de orden reducido) para la síntesis lógica y la verificación formal . [13]
Las oraciones lógicas que se pueden expresar en cálculo proposicional clásico tienen una expresión equivalente en álgebra de Boole. Por tanto, la lógica booleana se utiliza a veces para denotar el cálculo proposicional realizado de esta manera. [14] [15] [16] El álgebra booleana no es suficiente para capturar fórmulas lógicas utilizando cuantificadores , como los de la lógica de primer orden .
Aunque el desarrollo de la lógica matemática no siguió el programa de Boole, la conexión entre su álgebra y la lógica se afianzó más tarde en el ámbito de la lógica algebraica , que también estudia los sistemas algebraicos de muchas otras lógicas. [8] El problema de determinar si las variables de una fórmula booleana (proposicional) determinada se pueden asignar de tal manera que la fórmula se evalúe como verdadera se denomina problema de satisfacibilidad booleana (SAT) y es de importancia para la informática teórica . ciencia , siendo el primer problema que se ha demostrado que es NP-completo . El modelo de cálculo estrechamente relacionado conocido como circuito booleano relaciona la complejidad del tiempo (de un algoritmo ) con la complejidad del circuito .
Mientras que en álgebra elemental las expresiones denotan principalmente números , en álgebra de Boole denotan los valores de verdad falso y verdadero . Estos valores se representan con los bits 0 y 1. No se comportan como los números enteros 0 y 1, para los cuales 1 + 1 = 2 , pero pueden identificarse con los elementos del campo de dos elementos GF(2) , que es, módulo aritmético entero 2 , para el cual 1 + 1 = 0 . Luego, la suma y la multiplicación desempeñan los roles booleanos de XOR (o exclusivo) y AND (conjunción), respectivamente, con la disyunción x ∨ y (o inclusivo) definible como x + y − xy y la negación ¬ x como 1 − x . En GF(2) , − puede sustituirse por + , ya que denotan la misma operación; sin embargo, esta forma de escribir operaciones booleanas permite aplicar las operaciones aritméticas habituales de números enteros (esto puede resultar útil cuando se utiliza un lenguaje de programación en el que GF(2) no está implementado).
El álgebra booleana también se ocupa de funciones que tienen sus valores en el conjunto {0,1} . Una secuencia de bits es un ejemplo comúnmente utilizado de dicha función. Otro ejemplo común es la totalidad de subconjuntos de un conjunto E : para un subconjunto F de E , se puede definir la función indicadora que toma el valor 1 en F y 0 fuera de F. El ejemplo más general es el conjunto de elementos de un álgebra booleana , siendo todos los anteriores ejemplos de los mismos.
Como ocurre con el álgebra elemental, la parte puramente ecuacional de la teoría puede desarrollarse sin considerar valores explícitos para las variables. [17]
Las operaciones básicas del álgebra booleana son conjunción , disyunción y negación . Estas operaciones booleanas se expresan con los operadores binarios correspondientes ( Y y O ) y el operador unario ( NO ), denominados colectivamente operadores booleanos . [18]
Las operaciones booleanas básicas sobre las variables xey se definen de la siguiente manera:
Alternativamente, los valores de x ∧ y , x ∨ y y ¬ x se pueden expresar tabulando sus valores con tablas de verdad de la siguiente manera:
Si los valores de verdad 0 y 1 se interpretan como números enteros, estas operaciones pueden expresarse con las operaciones ordinarias de la aritmética (donde x + y usa la suma y xy usa la multiplicación), o mediante las funciones de mínimo/máximo:
Se podría considerar que sólo la negación y una de las otras dos operaciones son básicas debido a las siguientes identidades que permiten definir la conjunción en términos de negación y disyunción, y viceversa ( leyes de De Morgan ):
Las operaciones compuestas a partir de las operaciones básicas incluyen, entre otras, las siguientes:
Estas definiciones dan lugar a las siguientes tablas de verdad que dan los valores de estas operaciones para las cuatro entradas posibles.
Una ley del álgebra booleana es una identidad como x ∨ ( y ∨ z ) = ( x ∨ y ) ∨ z entre dos términos booleanos, donde un término booleano se define como una expresión construida a partir de variables y las constantes 0 y 1 usando las operaciones ∧, ∨ y ¬. El concepto se puede extender a términos que involucran otras operaciones booleanas como ⊕, → y ≡, pero tales extensiones son innecesarias para los propósitos a los que se aplican las leyes. Dichos propósitos incluyen la definición de álgebra booleana como cualquier modelo de las leyes booleanas y como medio para derivar nuevas leyes a partir de las antiguas, como en la derivación de x ∨ ( y ∧ z ) = x ∨ ( z ∧ y ) de y ∧ z = z ∧ y (como se trata en § Álgebra booleana axiomatizante ).
El álgebra booleana satisface muchas de las mismas leyes que el álgebra ordinaria cuando se compara ∨ con suma y ∧ con multiplicación. En particular, las siguientes leyes son comunes a ambos tipos de álgebra: [19] [20]
Las siguientes leyes se cumplen en el álgebra booleana, pero no en el álgebra ordinaria:
Tomar x = 2 en la tercera ley anterior muestra que no es una ley de álgebra ordinaria, ya que 2 × 2 = 4 . Las cinco leyes restantes se pueden refutar en álgebra ordinaria tomando todas las variables como 1. Por ejemplo, en la ley de absorción 1, el lado izquierdo sería 1(1 + 1) = 2 , mientras que el lado derecho sería 1 ( etcétera).
Todas las leyes tratadas hasta ahora han sido de conjunción y disyunción. Estas operaciones tienen la propiedad de que cambiar cualquiera de los argumentos deja la salida sin cambios o la salida cambia de la misma manera que la entrada. De manera equivalente, cambiar cualquier variable de 0 a 1 nunca da como resultado que la salida cambie de 1 a 0. Se dice que las operaciones con esta propiedad son monótonas . Por tanto, hasta ahora todos los axiomas han sido para la lógica booleana monótona. La no monotonicidad ingresa a través del complemento ¬ de la siguiente manera. [5]
La operación complementaria está definida por las dos leyes siguientes.
Todas las propiedades de la negación, incluidas las leyes siguientes, se derivan únicamente de las dos leyes anteriores. [5]
Tanto en el álgebra ordinaria como en el de Boole, la negación funciona mediante el intercambio de pares de elementos, por lo que en ambas álgebras satisface la ley de la doble negación (también llamada ley de involución).
Pero mientras que el álgebra ordinaria satisface las dos leyes
El álgebra booleana satisface las leyes de De Morgan :
Las leyes enumeradas anteriormente definen el álgebra booleana, en el sentido de que implican el resto del tema. Las leyes de complementación 1 y 2, junto con las leyes monótonas, son suficientes para este propósito y, por lo tanto, pueden considerarse como un posible conjunto completo de leyes o axiomatización del álgebra de Boole. Cada ley del álgebra de Boole se deriva lógicamente de estos axiomas. Además, las álgebras de Boole pueden definirse como los modelos de estos axiomas tal como se tratan en § Álgebras de Boole .
Escribir más leyes del álgebra de Boole no puede dar lugar a nuevas consecuencias de estos axiomas, ni puede descartar ningún modelo de ellos. Por el contrario, en una lista de algunas, pero no todas, las mismas leyes, podría haber habido leyes booleanas que no se derivaran de las de la lista y, además, habría habido modelos de las leyes enumeradas que no fueran álgebras booleanas.
Esta axiomatización no es de ninguna manera la única, ni necesariamente la más natural, dado que no se prestó atención a si algunos de los axiomas se derivaban de otros, sino que simplemente existía la opción de detenerse cuando se habían notado suficientes leyes y se habían tratado más a fondo. en § Axiomatizar el álgebra booleana . O bien, la noción intermedia de axioma puede eludirse por completo definiendo una ley booleana directamente como cualquier tautología , entendida como una ecuación que se cumple para todos los valores de sus variables superiores a 0 y 1. [21] [22] Todas estas definiciones de álgebra booleana pueden demostrarse que es equivalente.
Principio: Si {X, R} es un conjunto parcialmente ordenado , entonces {X, R(inverse)} también es un conjunto parcialmente ordenado.
No hay nada especial en la elección de símbolos para los valores del álgebra booleana. 0 y 1 podrían cambiarse de nombre a α y β , y siempre que se hiciera de manera consistente, seguiría siendo álgebra booleana, aunque con algunas diferencias cosméticas obvias.
Pero supongamos que 0 y 1 pasaron a llamarse 1 y 0 respectivamente. Entonces seguiría siendo álgebra booleana y, además, operaría con los mismos valores. Sin embargo, no sería idéntica a nuestra álgebra booleana original porque ahora ∨ se comporta como solía hacerlo ∧ y viceversa. Por lo tanto, todavía hay algunas diferencias cosméticas que muestran que la notación ha cambiado, a pesar de que todavía se utilizan 0 y 1.
Pero si además de intercambiar los nombres de los valores también se intercambian los nombres de las dos operaciones binarias, ahora no queda rastro de lo que se hizo. El producto final es completamente indistinguible de lo que se empezó. Las columnas para x ∧ y y x ∨ y en las tablas de verdad han cambiado de lugar, pero ese cambio es irrelevante.
Cuando los valores y las operaciones se pueden emparejar de una manera que deja todo lo importante sin cambios cuando todos los pares se cambian simultáneamente, los miembros de cada par se denominan duales entre sí. Por tanto, 0 y 1 son duales, y ∧ y ∨ son duales. El principio de dualidad , también llamado dualidad de De Morgan , afirma que el álgebra de Boole no cambia cuando se intercambian todos los pares duales.
Un cambio que no era necesario realizar como parte de este intercambio fue el de complementar. El complemento es una operación autodual . La operación de identidad o de no hacer nada x (copiar la entrada a la salida) también es autodual. Un ejemplo más complicado de una operación autodual es ( x ∧ y ) ∨ ( y ∧ z ) ∨ ( z ∧ x ) . No existe una operación binaria autodual que dependa de ambos argumentos. Una composición de operaciones autoduales es una operación autodual. Por ejemplo, si f ( x , y , z ) = ( x ∧ y ) ∨ ( y ∧ z ) ∨ ( z ∧ x ) , entonces f ( f ( x , y , z ), x , t ) es un yo -Operación dual de cuatro argumentos x , y , z , t .
El principio de dualidad puede explicarse desde la perspectiva de la teoría de grupos por el hecho de que hay exactamente cuatro funciones que son asignaciones uno a uno ( automorfismos ) del conjunto de polinomios booleanos a sí mismo: la función identidad, la función complemento, la función dual y la función contradual (dual complementada). Estas cuatro funciones forman un grupo bajo composición de funciones , isomorfo al grupo de cuatro de Klein , que actúa sobre el conjunto de polinomios booleanos. Walter Gottschalk comentó que en consecuencia un nombre más apropiado para el fenómeno sería principio ( o cuadrado ) de cuaternalidad . [5] : 21-22
Se puede utilizar un diagrama de Venn [23] como representación de una operación booleana utilizando regiones superpuestas sombreadas. Hay una región para cada variable, todas circulares en los ejemplos aquí. El interior y el exterior de la región x corresponden respectivamente a los valores 1 (verdadero) y 0 (falso) para la variable x . El sombreado indica el valor de la operación para cada combinación de regiones, donde oscuro denota 1 y claro 0 (algunos autores usan la convención opuesta).
Los tres diagramas de Venn en la figura siguiente representan respectivamente la conjunción x ∧ y , la disyunción x ∨ y y el complemento ¬ x .
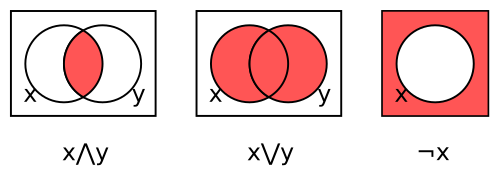
Para la conjunción, la región dentro de ambos círculos se sombrea para indicar que x ∧ y es 1 cuando ambas variables son 1. Las otras regiones se dejan sin sombrear para indicar que x ∧ y es 0 para las otras tres combinaciones.
El segundo diagrama representa la disyunción x ∨ y sombreando aquellas regiones que se encuentran dentro de uno o ambos círculos. El tercer diagrama representa el complemento ¬ x sombreando la región que no está dentro del círculo.
Si bien no hemos mostrado los diagramas de Venn para las constantes 0 y 1, son triviales, ya que son respectivamente un cuadro blanco y un cuadro oscuro, y ninguno de ellos contiene un círculo. Sin embargo, podríamos poner un círculo para x en esos cuadros, en cuyo caso cada uno denotaría una función de un argumento, x , que devuelve el mismo valor independientemente de x , llamada función constante. En lo que respecta a sus resultados, las constantes y las funciones constantes son indistinguibles; la diferencia es que una constante no toma argumentos, lo que se denomina operación cero o nula , mientras que una función constante toma un argumento, que ignora, y es una operación unaria .
Los diagramas de Venn son útiles para visualizar leyes. Las leyes de conmutatividad para ∧ y ∨ se pueden ver a partir de la simetría de los diagramas: una operación binaria que no fuera conmutativa no tendría un diagrama simétrico porque intercambiar x e y tendría el efecto de reflejar el diagrama horizontalmente y cualquier falla de conmutatividad entonces aparece como una falla de simetría.
La idempotencia de ∧ y ∨ se puede visualizar deslizando los dos círculos juntos y observando que el área sombreada se convierte en el círculo completo, tanto para ∧ como para ∨.
Para ver la primera ley de absorción, x ∧ ( x ∨ y ) = x , comience con el diagrama del medio para x ∨ y y observe que la porción del área sombreada en común con el círculo x es la totalidad del círculo x . Para la segunda ley de absorción, x ∨ ( x ∧ y ) = x , comience con el diagrama de la izquierda para x ∧ y y observe que sombrear todo el círculo x da como resultado que solo se sombree el círculo x , ya que el sombreado anterior estaba dentro el círculo x .
La ley de la doble negación se puede ver complementando el sombreado en el tercer diagrama para ¬ x , que sombrea el círculo x .
Para visualizar la primera ley de De Morgan, (¬ x ) ∧ (¬ y ) = ¬( x ∨ y ) , comience con el diagrama del medio para x ∨ y y complemente su sombreado de modo que solo se sombree la región fuera de ambos círculos, que es lo que describe el lado derecho de la ley. El resultado es el mismo que si sombreáramos esa región que está tanto fuera del círculo x como fuera del círculo y , es decir, la conjunción de sus exteriores, que es lo que describe el lado izquierdo de la ley.
La segunda ley de De Morgan, (¬ x ) ∨ (¬ y ) = ¬( x ∧ y ) , funciona de la misma manera con los dos diagramas intercambiados.
La primera ley del complemento, x ∧ ¬ x = 0 , dice que el interior y el exterior del círculo x no se superponen. La segunda ley del complemento, x ∨ ¬ x = 1 , dice que todo está dentro o fuera del círculo x .
La lógica digital es la aplicación del álgebra booleana de 0 y 1 al hardware electrónico que consta de puertas lógicas conectadas para formar un diagrama de circuito . Cada puerta implementa una operación booleana y se representa esquemáticamente mediante una forma que indica la operación. Las formas asociadas con las puertas para conjunción (puertas AND), disyunción (puertas OR) y complemento (inversores) son las siguientes: [24]
Las líneas a la izquierda de cada puerta representan cables o puertos de entrada . El valor de la entrada está representado por un voltaje en el cable. Para la llamada lógica "activa-alta", 0 está representado por un voltaje cercano a cero o "tierra", mientras que 1 está representado por un voltaje cercano al voltaje de suministro; active-low invierte esto. La línea a la derecha de cada puerta representa el puerto de salida, que normalmente sigue las mismas convenciones de voltaje que los puertos de entrada.
El complemento se implementa con una puerta inversora. El triángulo denota la operación que simplemente copia la entrada a la salida; el pequeño círculo en la salida denota la inversión real que complementa la entrada. La convención de poner un círculo de este tipo en cualquier puerto significa que la señal que pasa a través de este puerto se complementa en el camino, ya sea un puerto de entrada o de salida.
Se puede entender que el principio de dualidad, o leyes de De Morgan , afirma que complementar los tres puertos de una puerta Y la convierte en una puerta O y viceversa, como se muestra en la Figura 4 a continuación. Sin embargo, complementar ambos puertos de un inversor deja el funcionamiento sin cambios.
De manera más general, se puede complementar cualquiera de los ocho subconjuntos de los tres puertos de una puerta AND u OR. Las dieciséis posibilidades resultantes dan lugar a sólo ocho operaciones booleanas, es decir, aquellas con un número impar de unos en su tabla de verdad. Hay ocho, porque el "bit impar" puede ser 0 o 1 y puede ocupar cualquiera de las cuatro posiciones de la tabla de verdad. Habiendo dieciséis operaciones booleanas binarias, esto debe dejar ocho operaciones con un número par de unos en sus tablas de verdad. Dos de ellas son las constantes 0 y 1 (como operaciones binarias que ignoran ambas entradas); cuatro son las operaciones que dependen de manera no trivial exactamente de una de sus dos entradas, a saber, x , y , ¬x y ¬y ; y los dos restantes son x ⊕ y (XOR) y su complemento x ≡ y .
El término "álgebra" denota tanto un sujeto, es decir, el sujeto del álgebra , como un objeto, es decir, una estructura algebraica . Mientras que lo anterior ha abordado el tema del álgebra de Boole, esta sección trata de objetos matemáticos llamados álgebras de Boole, definidas con total generalidad como cualquier modelo de las leyes de Boole. Comenzamos con un caso especial de la noción definible sin referencia a las leyes, a saber, álgebras booleanas concretas, y luego damos la definición formal de la noción general.
Un álgebra booleana concreta o un campo de conjuntos es cualquier conjunto no vacío de subconjuntos de un conjunto dado X cerrado bajo las operaciones de conjunto de unión , intersección y complemento relativo a X. [5]
(Históricamente, también se requería que X no estuviera vacío para excluir el álgebra booleana degenerada o de un elemento, que es la única excepción a la regla de que todas las álgebras booleanas satisfacen las mismas ecuaciones, ya que el álgebra degenerada satisface todas las ecuaciones. Sin embargo, esta exclusión entra en conflicto con la definición puramente ecuacional preferida de "álgebra de Boole", ya que no hay forma de descartar el álgebra de un elemento usando solo ecuaciones: 0 ≠ 1 no cuenta, ya que es una ecuación negada. Por lo tanto, los autores modernos permiten el álgebra de Boole degenerada y sea X vacío.)
Ejemplo 1. El conjunto potencia 2 X de X , que consta de todos los subconjuntos de X . Aquí X puede ser cualquier conjunto: vacío, finito, infinito o incluso incontable .
Ejemplo 2. El conjunto vacío y X . Este álgebra de dos elementos muestra que un álgebra booleana concreta puede ser finita incluso cuando consta de subconjuntos de un conjunto infinito. Se puede ver que todo campo de subconjuntos de X debe contener el conjunto vacío y X . Por lo tanto, no es posible ningún ejemplo más pequeño que el álgebra degenerada obtenida tomando X como vacío para hacer que el conjunto vacío y X coincidan.
Ejemplo 3. El conjunto de conjuntos finitos y cofinitos de números enteros, donde un conjunto cofinito es aquel que omite sólo un número finito de números enteros. Esto está claramente cerrado bajo complemento y está cerrado bajo unión porque la unión de un conjunto cofinito con cualquier conjunto es cofinita, mientras que la unión de dos conjuntos finitos es finita. La intersección se comporta como una unión con "finito" y "cofinito" intercambiados. Este ejemplo es contablemente infinito porque sólo hay un número contable de conjuntos finitos de números enteros.
Ejemplo 4. Para un ejemplo menos trivial del punto planteado en el ejemplo 2, considere un diagrama de Venn formado por n curvas cerradas que dividen el diagrama en 2 n regiones, y sea X el conjunto (infinito) de todos los puntos en el plano que no están en cualquier curva excepto en algún lugar dentro del diagrama. El interior de cada región es, por tanto, un subconjunto infinito de X , y cada punto de X está exactamente en una región. Entonces, el conjunto de todas las 2 2 n posibles uniones de regiones (incluido el conjunto vacío obtenido como la unión del conjunto vacío de regiones y X obtenido como la unión de las 2 n regiones) está cerrado bajo unión, intersección y complemento en relación con X y por tanto forma un álgebra booleana concreta. Nuevamente, hay un número finito de subconjuntos de un conjunto infinito que forma un álgebra booleana concreta, y el ejemplo 2 surge como el caso n = 0 sin curvas.
Un subconjunto Y de X se puede identificar con una familia indexada de bits con conjunto de índices X , siendo el bit indexado por x ∈ X 1 o 0 según sea o no x ∈ Y . (Esta es la llamada noción de función característica de un subconjunto). Por ejemplo, una palabra de computadora de 32 bits consta de 32 bits indexados por el conjunto {0,1,2,...,31}, con 0 y 31 indexar los bits de orden bajo y alto respectivamente. Para un ejemplo más pequeño, si a , b, c se ven como posiciones de bits en ese orden de izquierda a derecha, los ocho subconjuntos {}, { c }, { b }, { b , c }, { a }, { a , c }, { a , b } y { a , b , c } de X se pueden identificar con los respectivos vectores de bits 000, 001, 010, 011, 100, 101, 110 y 111. Vectores de bits indexados por el conjunto de números naturales son secuencias infinitas de bits, mientras que los indexados por los reales en el intervalo unitario [0,1] están demasiado densamente empaquetados para poder escribirlos de manera convencional, pero aun así forman familias indexadas bien definidas (imagínese colorear cada punto de el intervalo [0,1] ya sea negro o blanco independientemente; los puntos negros forman entonces un subconjunto arbitrario de [0,1]).
Desde este punto de vista de vector de bits, un álgebra booleana concreta se puede definir de manera equivalente como un conjunto no vacío de vectores de bits, todos de la misma longitud (más generalmente, indexados por el mismo conjunto) y cerrados bajo las operaciones de vectores de bits de bit a bit ∧, ∨ y ¬, como en 1010∧0110 = 0010 , 1010∨0110 = 1110 y ¬1010 = 0101 , las realizaciones de vectores de bits de intersección, unión y complemento respectivamente.
El conjunto {0,1} y sus operaciones booleanas tratadas anteriormente pueden entenderse como el caso especial de vectores de bits de longitud uno, que mediante la identificación de vectores de bits con subconjuntos también pueden entenderse como los dos subconjuntos de un elemento de un solo elemento. colocar. Esto se denomina álgebra booleana prototípica y se justifica por la siguiente observación.
Esta observación se prueba de la siguiente manera. Ciertamente, cualquier ley satisfecha por todas las álgebras booleanas concretas lo es también por la prototípica, ya que es concreta. A la inversa, cualquier ley que falle en algún álgebra booleana concreta debe haber fallado en una posición de bit particular, en cuyo caso esa posición por sí sola proporciona un contraejemplo de un bit para esa ley. La no degeneración asegura la existencia de al menos una posición de bit porque solo hay un vector de bit vacío.
El objetivo final de la siguiente sección puede entenderse como eliminar el "concreto" de la observación anterior. Ese objetivo se alcanza mediante la observación más contundente de que, hasta el isomorfismo, todas las álgebras de Boole son concretas.
Hasta ahora, todas las álgebras de Boole han sido concretas y consisten en vectores de bits o, equivalentemente, en subconjuntos de algún conjunto. Tal álgebra booleana consta de un conjunto y operaciones sobre ese conjunto que se puede demostrar que satisfacen las leyes del álgebra booleana.
En lugar de mostrar que se satisfacen las leyes booleanas, podemos postular un conjunto X , dos operaciones binarias sobre X y una operación unaria, y exigir que esas operaciones satisfagan las leyes del álgebra booleana. Los elementos de X no necesitan ser vectores o subconjuntos de bits, sino que pueden ser cualquier cosa. Esto lleva a la definición abstracta más general .
A los efectos de esta definición, es irrelevante cómo las operaciones llegaron a satisfacer las leyes, ya sea por decreto o por prueba. Todas las álgebras de Boole concretas satisfacen las leyes (por prueba y no por decreto), por lo que cada álgebra de Boole concreta es un álgebra de Boole según nuestras definiciones. Esta definición axiomática de un álgebra booleana como un conjunto y ciertas operaciones que satisfacen ciertas leyes o axiomas por decreto es completamente análoga a las definiciones abstractas de grupo , anillo , campo , etc., características del álgebra moderna o abstracta .
Dada cualquier axiomatización completa del álgebra booleana, como los axiomas de una red distributiva complementada , una condición suficiente para que una estructura algebraica de este tipo satisfaga todas las leyes booleanas es que satisfaga sólo esos axiomas. Por lo tanto, la siguiente es una definición equivalente.
La sección sobre axiomatización enumera otras axiomatizaciones, cualquiera de las cuales puede constituir la base de una definición equivalente.
Aunque todo álgebra booleana concreta es un álgebra booleana, no todas las álgebras booleanas necesitan ser concretas. Sea n un entero positivo sin cuadrados , no divisible por el cuadrado de un número entero, por ejemplo 30 pero no 12. Las operaciones de máximo común divisor , mínimo común múltiplo y división en n (es decir, ¬ x = n / x ), se puede demostrar que satisface todas las leyes booleanas cuando sus argumentos abarcan más de los divisores positivos de n . Por tanto, esos divisores forman un álgebra booleana. Estos divisores no son subconjuntos de un conjunto, lo que convierte a los divisores de n en un álgebra booleana que no es concreta según nuestras definiciones.
Sin embargo, si cada divisor de n está representado por el conjunto de sus factores primos, esta álgebra booleana no concreta es isomorfa al álgebra booleana concreta que consta de todos los conjuntos de factores primos de n , con unión correspondiente al mínimo común múltiplo, intersección con el máximo común divisor y complemento de la división en n . Entonces, este ejemplo, aunque no es técnicamente concreto, es al menos "moralmente" concreto a través de esta representación, llamada isomorfismo . Este ejemplo es un ejemplo de la siguiente noción.
La siguiente pregunta se responde positivamente de la siguiente manera.
Es decir, hasta el isomorfismo, las álgebras booleanas abstractas y concretas son la misma cosa. Este resultado depende del teorema del ideal primo booleano , un principio de elección ligeramente más débil que el axioma de elección . Esta fuerte relación implica un resultado más débil que fortalece la observación en la subsección anterior a la siguiente consecuencia fácil de representabilidad.
Es más débil en el sentido de que no implica por sí mismo representabilidad. Las álgebras de Boole son especiales aquí, por ejemplo, un álgebra de relaciones es un álgebra de Boole con estructura adicional, pero no es cierto que cada álgebra de relaciones sea representable en el sentido apropiado para las álgebras de relaciones.
La definición anterior de un álgebra booleana abstracta como un conjunto junto con operaciones que satisfacen "las" leyes booleanas plantea la cuestión de cuáles son esas leyes. Una respuesta simplista es "todas las leyes booleanas", que pueden definirse como todas las ecuaciones que se cumplen para el álgebra booleana de 0 y 1. Sin embargo, dado que existen infinitas leyes de este tipo, esta no es una respuesta satisfactoria en la práctica, lo que lleva a la Para ello basta con requerir sólo un número finito de leyes para que se cumpla.
En el caso de las álgebras de Boole, la respuesta es "sí": las ecuaciones finitas enumeradas anteriormente son suficientes. Por tanto, se dice que el álgebra de Boole es finitamente axiomatizable o de base finita .
Además, el número de ecuaciones necesarias se puede reducir aún más. Para empezar, algunas de las leyes anteriores están implícitas en algunas de las otras. Un subconjunto suficiente de las leyes anteriores consta de los pares de leyes de asociatividad, conmutatividad y absorción, la distributividad de ∧ sobre ∨ (u la otra ley de distributividad; una es suficiente) y las dos leyes del complemento. De hecho, esta es la axiomatización tradicional del álgebra booleana como una red distributiva complementada .
Al introducir leyes adicionales no enumeradas anteriormente, es posible acortar aún más la lista de ecuaciones necesarias; por ejemplo, con la barra vertical que representa la operación del trazo de Sheffer , el axioma único es suficiente para axiomatizar completamente el álgebra booleana. También es posible encontrar axiomas únicos más largos utilizando operaciones más convencionales; consulte Axiomas mínimos para el álgebra booleana . [26]
La lógica proposicional es un sistema lógico que está íntimamente relacionado con el álgebra de Boole. [5] Muchos conceptos sintácticos del álgebra booleana se trasladan a la lógica proposicional con solo cambios menores en notación y terminología, mientras que la semántica de la lógica proposicional se define a través de álgebras booleanas de manera que las tautologías (teoremas) de la lógica proposicional corresponden a teoremas ecuacionales. del álgebra booleana.
Sintácticamente, cada término booleano corresponde a una fórmula proposicional de la lógica proposicional. En esta traducción entre álgebra booleana y lógica proposicional, las variables booleanas x, y, ... se convierten en variables proposicionales (o átomos ) P, Q ,... Términos booleanos como x ∨ y se convierten en fórmulas proposicionales P ∨ Q ; 0 se vuelve falso o ⊥ y 1 se vuelve verdadero o T . Es conveniente cuando se hace referencia a proposiciones genéricas utilizar las letras griegas Φ, Ψ, ... como metavariables (variables fuera del lenguaje del cálculo proposicional, utilizadas cuando se habla de cálculo proposicional) para denotar proposiciones.
La semántica de la lógica proposicional se basa en asignaciones de verdad . La idea esencial de una asignación de verdad es que las variables proposicionales se asignan a elementos de un álgebra booleana fija, y luego el valor de verdad de una fórmula proposicional que usa estas letras es el elemento del álgebra booleana que se obtiene calculando el valor de la Término booleano correspondiente a la fórmula. En la semántica clásica, sólo se utiliza el álgebra booleana de dos elementos, mientras que en la semántica con valores booleanos se consideran álgebras booleanas arbitrarias. Una tautología es una fórmula proposicional a la que se le asigna un valor de verdad 1 por cada asignación de verdad de sus variables proposicionales a un álgebra booleana arbitraria (o, de manera equivalente, cada asignación de verdad al álgebra booleana de dos elementos).
Esta semántica permite una traducción entre tautologías de la lógica proposicional y teoremas ecuacionales del álgebra de Boole. Toda tautología Φ de la lógica proposicional se puede expresar como la ecuación booleana Φ = 1, que será un teorema del álgebra booleana. Por el contrario, todo teorema Φ = Ψ del álgebra booleana corresponde a las tautologías (Φ ∨ ¬Ψ) ∧ (¬Φ ∨ Ψ) y (Φ ∧ Ψ) ∨ (¬Φ ∧ ¬Ψ). Si → está en el lenguaje, estas últimas tautologías también pueden escribirse como (Φ → Ψ) ∧ (Ψ → Φ), o como dos teoremas separados Φ → Ψ y Ψ → Φ; si ≡ está disponible, entonces se puede utilizar la tautología única Φ ≡ Ψ.
Una aplicación motivadora del cálculo proposicional es el análisis de proposiciones y argumentos deductivos en lenguaje natural. [27] Mientras que la proposición "si x = 3, entonces x + 1 = 4" depende de los significados de símbolos tales como + y 1, la proposición "si x = 3, entonces x = 3" no; es cierto simplemente en virtud de su estructura, y sigue siendo cierto tanto si " x = 3" se reemplaza por " x = 4" como si "la luna está hecha de queso verde". La forma genérica o abstracta de esta tautología es "si P , entonces P ", o en el lenguaje del álgebra booleana, P → P. [ cita necesaria ]
Reemplazar P por x = 3 o cualquier otra proposición se llama instanciación de P por esa proposición. El resultado de instanciar P en una proposición abstracta se llama instancia de la proposición. Por tanto, x = 3 → x = 3 es una tautología en virtud de ser un ejemplo de la tautología abstracta P → P . Todas las apariciones de la variable instanciada deben instanciarse con la misma proposición, para evitar tonterías como P → x = 3 o x = 3 → x = 4.
El cálculo proposicional restringe la atención a las proposiciones abstractas, aquellas construidas a partir de variables proposicionales mediante operaciones booleanas. La creación de instancias todavía es posible dentro del cálculo proposicional, pero solo instanciando variables proposicionales mediante proposiciones abstractas, como instanciar Q por Q → P en P → ( Q → P ) para producir la instancia P → (( Q → P ) → P ).
(La disponibilidad de instanciación como parte de la maquinaria del cálculo proposicional evita la necesidad de metavariables dentro del lenguaje del cálculo proposicional, ya que las variables proposicionales ordinarias pueden considerarse dentro del lenguaje para denotar proposiciones arbitrarias. Las metavariables mismas están fuera del alcance de la instanciación, no es parte del lenguaje del cálculo proposicional sino más bien parte del mismo lenguaje para hablar sobre ello en el que está escrita esta oración, donde es necesario poder distinguir las variables proposicionales y sus instancias como entidades sintácticas distintas).
Una axiomatización del cálculo proposicional es un conjunto de tautologías llamadas axiomas y una o más reglas de inferencia para producir nuevas tautologías a partir de las antiguas. Una prueba en un sistema de axiomas A es una secuencia finita no vacía de proposiciones, cada una de las cuales es una instancia de un axioma de A o se sigue por alguna regla de A a partir de proposiciones que aparecen anteriormente en la prueba (lo que no permite el razonamiento circular). La última proposición es el teorema demostrado por la prueba. Cada segmento inicial no vacío de una prueba es en sí mismo una prueba, de donde cada proposición en una prueba es en sí misma un teorema. Una axiomatización es sólida cuando cada teorema es una tautología, y completa cuando cada tautología es un teorema. [28]
El cálculo proposicional se organiza comúnmente como un sistema de Hilbert , cuyas operaciones son justamente las del álgebra booleana y cuyos teoremas son tautologías booleanas, aquellos términos booleanos iguales a la constante booleana 1. Otra forma es el cálculo secuente , que tiene dos tipos, proposiciones como en las proposiciones ordinarias. cálculo proposicional y pares de listas de proposiciones llamadas secuentes , como A ∨ B , A ∧ C , ... ⊢ A , B → C , .... Las dos mitades de un secuente se llaman antecedente y sucesor respectivamente . La metavariable habitual que denota un antecedente o parte del mismo es Γ, y para un sucesor Δ; por lo tanto, Γ, A ⊢ Δ denotaría un secuente cuyo sucesor es una lista Δ y cuyo antecedente es una lista Γ con una proposición adicional A añadida después. El antecedente se interpreta como la conjunción de sus proposiciones, el sucedente como la disyunción de sus proposiciones y el secuente mismo como la implicación del sucedente por el antecedente.
La vinculación difiere de la implicación en que mientras que la última es una operación binaria que devuelve un valor en un álgebra booleana, la primera es una relación binaria que se cumple o no. En este sentido, la implicación es una forma externa de implicación, es decir, externa al álgebra de Boole, pensando en el lector del secuente como también externo e interpretando y comparando antecedentes y sucesores en algún álgebra de Boole. La interpretación natural de ⊢ es como ≤ en el orden parcial del álgebra booleana definida por x ≤ y justo cuando x ∨ y = y . Esta capacidad de mezclar implicación externa ⊢ e implicación interna → en una sola lógica se encuentra entre las diferencias esenciales entre el cálculo secuencial y el cálculo proposicional. [29]
El álgebra booleana como cálculo de dos valores es fundamental para los circuitos de computadora, la programación de computadoras y la lógica matemática, y también se usa en otras áreas de las matemáticas, como la teoría de conjuntos y la estadística. [5]
A principios del siglo XX, varios ingenieros eléctricos [ ¿quién? ] reconoció intuitivamente que el álgebra de Boole era análoga al comportamiento de ciertos tipos de circuitos eléctricos. Claude Shannon demostró formalmente que tal comportamiento era lógicamente equivalente al álgebra booleana en su tesis de maestría de 1937, Un análisis simbólico de circuitos de conmutación y relés .
Hoy en día, todas las computadoras modernas de uso general realizan sus funciones utilizando lógica booleana de dos valores; es decir, sus circuitos eléctricos son una manifestación física de la lógica booleana de dos valores. Lo logran de varias maneras: como voltajes en cables en circuitos de alta velocidad y dispositivos de almacenamiento capacitivos, como orientaciones de un dominio magnético en dispositivos de almacenamiento ferromagnéticos, como agujeros en tarjetas perforadas o cintas de papel , etc. (Algunas de las primeras computadoras usaban circuitos o mecanismos decimales en lugar de circuitos lógicos de dos valores).
Por supuesto, es posible codificar más de dos símbolos en cualquier medio determinado. Por ejemplo, se podrían utilizar respectivamente 0, 1, 2 y 3 voltios para codificar un alfabeto de cuatro símbolos en un cable, o agujeros de diferentes tamaños en una tarjeta perforada. En la práctica, las estrictas limitaciones de alta velocidad, tamaño pequeño y baja potencia se combinan para hacer que el ruido sea un factor importante. Esto hace que sea difícil distinguir entre símbolos cuando hay varios símbolos posibles que podrían aparecer en un solo sitio. En lugar de intentar distinguir entre cuatro voltajes en un cable, los diseñadores digitales se han decidido por dos voltajes por cable, alto y bajo.
Las computadoras utilizan circuitos booleanos de dos valores por las razones anteriores. Las arquitecturas informáticas más comunes utilizan secuencias ordenadas de valores booleanos, llamados bits, de 32 o 64 valores, por ejemplo, 01101000110101100101010101001011. Cuando se programa en código de máquina , lenguaje ensamblador y algunos otros lenguajes de programación , los programadores trabajan con la estructura digital de bajo nivel del registros de datos . Estos registros operan con voltajes, donde cero voltios representa el booleano 0 y un voltaje de referencia (a menudo +5 V, +3,3 V o +1,8 V) representa el booleano 1. Estos lenguajes admiten operaciones tanto numéricas como lógicas. En este contexto, "numérico" significa que la computadora trata secuencias de bits como números binarios (números de base dos) y ejecuta operaciones aritméticas como sumar, restar, multiplicar o dividir. "Lógico" se refiere a las operaciones lógicas booleanas de disyunción, conjunción y negación entre dos secuencias de bits, en las que cada bit de una secuencia se compara simplemente con su homólogo de la otra secuencia. Por lo tanto, los programadores tienen la opción de trabajar y aplicar las reglas del álgebra numérica o del álgebra booleana según sea necesario. Una característica diferenciadora central entre estas familias de operaciones es la existencia de la operación de acarreo en la primera pero no en la segunda.
Otras áreas donde dos valores es una buena opción son el derecho y las matemáticas. En una conversación relajada cotidiana, se aceptan respuestas complejas o matizadas como "tal vez" o "sólo el fin de semana". Sin embargo, en situaciones más específicas, como un tribunal de justicia o matemáticas basadas en teoremas, se considera ventajoso formular las preguntas de manera que admitan una respuesta simple de sí o no: ¿es el acusado culpable o no culpable? ¿Es verdadera la proposición? o falso, y rechazar cualquier otra respuesta. Sin embargo, lo que podría resultar limitante en la práctica para el encuestado, es que el principio de la pregunta simple de sí o no se ha convertido en una característica central de la lógica tanto judicial como matemática, lo que hace que la lógica de dos valores merezca organización y estudio por derecho propio.
Un concepto central de la teoría de conjuntos es la membresía. Una organización puede permitir múltiples grados de membresía, como principiante, asociado y pleno. Sin embargo, con los conjuntos, un elemento está dentro o fuera. Los candidatos a ser miembros de un conjunto funcionan igual que los cables de una computadora digital: cada candidato es miembro o no miembro, del mismo modo que cada cable es alto o bajo.
Siendo el álgebra una herramienta fundamental en cualquier área susceptible de tratamiento matemático, estas consideraciones se combinan para hacer que el álgebra de dos valores sea de fundamental importancia para el hardware de la computadora, la lógica matemática y la teoría de conjuntos.
La lógica de dos valores se puede extender a la lógica de múltiples valores , en particular reemplazando el dominio booleano {0, 1} con el intervalo unitario [0,1], en cuyo caso, en lugar de tomar solo valores 0 o 1, cualquier valor entre y Se puede suponer que incluyen 0 y 1. Algebraicamente, la negación (NO) se reemplaza con 1 − x , la conjunción (Y) se reemplaza con la multiplicación ( xy ) y la disyunción (O) se define mediante la ley de De Morgan . La interpretación de estos valores como valores de verdad lógicos produce una lógica multivalor, que forma la base de la lógica difusa y la lógica probabilística . En estas interpretaciones, un valor se interpreta como el "grado" de verdad: hasta qué punto una proposición es verdadera o la probabilidad de que la proposición sea verdadera.
La aplicación original de las operaciones booleanas fue la lógica matemática , donde combina los valores de verdad, verdaderos o falsos, de fórmulas individuales.
Los lenguajes naturales como el inglés tienen palabras para varias operaciones booleanas, en particular conjunción ( y ), disyunción ( o ), negación ( no ) e implicación ( implica ). Pero no es sinónimo de y no . Cuando se utilizan para combinar afirmaciones situacionales como "el bloque está sobre la mesa" y "los gatos beben leche", que ingenuamente son verdaderas o falsas, los significados de estos conectivos lógicos a menudo tienen el significado de sus contrapartes lógicas. Sin embargo, con descripciones de comportamiento como "Jim cruzó la puerta", se empiezan a notar diferencias como fallo de conmutatividad, por ejemplo, la conjunción de "Jim abrió la puerta" con "Jim cruzó la puerta" en ese orden. no es equivalente a su conjunción en el otro orden, ya que y generalmente significa y luego en tales casos. Las preguntas pueden ser similares: el orden "¿El cielo es azul y por qué el cielo es azul?" tiene más sentido que el orden inverso. Las órdenes conjuntivas sobre la conducta son como afirmaciones conductuales, como vestirse e ir a la escuela . Los mandatos disyuntivos como ámame o déjame o pescar o cortar el cebo tienden a ser asimétricos a través de la implicación de que una alternativa es menos preferible. Los sustantivos combinados como té y leche generalmente describen la agregación como una unión fija, mientras que el té o la leche son una opción. Sin embargo, el contexto puede revertir estos sentidos, ya que sus opciones son café y té, lo que generalmente significa lo mismo que sus opciones son café o té (alternativas). La doble negación, como en "No me gusta la leche", rara vez significa literalmente "Me gusta la leche", sino que más bien transmite algún tipo de cobertura, como para implicar que existe una tercera posibilidad. "No, no P" puede interpretarse libremente como "seguramente P", y aunque P implica necesariamente "no, no P ", lo contrario es sospechoso en inglés, al igual que con la lógica intuicionista . En vista del uso altamente idiosincrásico de las conjunciones en los lenguajes naturales, el álgebra booleana no puede considerarse un marco confiable para interpretarlas.
Las operaciones booleanas se utilizan en lógica digital para combinar los bits transportados en cables individuales, interpretándolos así en {0,1}. Cuando se utiliza un vector de n puertas binarias idénticas para combinar dos vectores de bits, cada uno de n bits, las operaciones de bits individuales pueden entenderse colectivamente como una operación única sobre valores de un álgebra booleana con 2 n elementos.
La teoría ingenua de conjuntos interpreta que las operaciones booleanas actúan sobre subconjuntos de un conjunto dado X. Como vimos anteriormente, este comportamiento es exactamente paralelo a las combinaciones de vectores de bits en cuanto a coordenadas, donde la unión de dos conjuntos corresponde a la disyunción de dos vectores de bits, y así sucesivamente.
El álgebra booleana libre de 256 elementos en tres generadores se implementa en pantallas de computadora basadas en gráficos rasterizados , que utilizan bit blit para manipular regiones enteras que consisten en píxeles , basándose en operaciones booleanas para especificar cómo se debe combinar la región de origen con la de destino, generalmente con la ayuda de una tercera región llamada máscara . Las tarjetas de video modernas ofrecen 2 2 3 = 256 operaciones ternarias para este propósito, siendo la elección de la operación un parámetro de un byte (8 bits). Las constantes SRC = 0xaa o 0b10101010 , DST = 0xcc o 0b11001100 y MSK = 0xf0 o 0b11110000 permiten que operaciones booleanas como (es decir, XOR el origen y el destino y luego AND el resultado con la máscara) se escriban directamente como una constante que denota una byte calculado en tiempo de compilación, 0x80 en el ejemplo, 0x88 si es solo , etc. En tiempo de ejecución, la tarjeta de video interpreta el byte como la operación ráster indicada por la expresión original de una manera uniforme que requiere notablemente poco hardware y que requiere tiempo completamente independiente. de la complejidad de la expresión.(SRC^DST)&MSK(SRC^DST)&MSKSRC^DST
Los sistemas de modelado de sólidos para diseño asistido por computadora ofrecen una variedad de métodos para construir objetos a partir de otros objetos, siendo uno de ellos la combinación mediante operaciones booleanas. En este método, el espacio en el que existen los objetos se entiende como un conjunto S de vóxeles (el análogo tridimensional de los píxeles en gráficos bidimensionales) y las formas se definen como subconjuntos de S , lo que permite combinar objetos como conjuntos mediante unión. intersección, etc. Un uso obvio es construir una forma compleja a partir de formas simples simplemente como la unión de estas últimas. Otro uso es en la escultura entendida como remoción de material: cualquier operación de rectificado, fresado, fresado o taladrado que pueda realizarse con maquinaria física sobre materiales físicos puede simularse en el ordenador con la operación booleana x ∧ ¬ y o x − y , que en la teoría de conjuntos es diferencia de conjuntos, elimine los elementos de y de los de x . Así, dadas dos formas, una para mecanizar y la otra el material a eliminar, el resultado de mecanizar la primera para eliminar la segunda se describe simplemente como su diferencia establecida.
Las consultas de los motores de búsqueda también emplean lógica booleana. Para esta aplicación, cada página web de Internet puede considerarse como un "elemento" de un "conjunto". Los siguientes ejemplos utilizan una sintaxis compatible con Google . [Nota 1]
"Término de búsqueda 1" "Término de búsqueda 2"
"Término de búsqueda 1" O "Término de búsqueda 2"
"Término de búsqueda 1" −"Término de búsqueda 2"