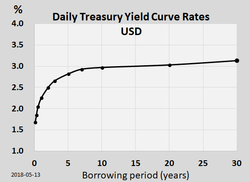


En finanzas , la curva de rendimiento es un gráfico que muestra cómo varían los rendimientos de los instrumentos de deuda, como los bonos, en función de los años restantes hasta el vencimiento . [1] [2] Normalmente, el eje horizontal o x del gráfico es una línea de tiempo de meses o años restantes hasta el vencimiento, con el vencimiento más corto a la izquierda y períodos de tiempo progresivamente más largos a la derecha. El eje vertical o y representa el rendimiento anualizado hasta el vencimiento. [3]
Quienes emiten y comercializan formas de deuda, como préstamos y bonos, utilizan curvas de rendimiento para determinar su valor. [4] Se cree que los cambios en la forma y la pendiente de la curva de rendimiento están relacionados con las expectativas de los inversores sobre la economía y las tasas de interés.
Ronald Melicher y Merle Welshans han identificado varias características de una curva de rendimiento correctamente construida. Debe basarse en un conjunto de valores que tienen diferentes períodos de vencimiento y todos los rendimientos deben calcularse en el mismo momento. Todos los valores medidos en la curva de rendimiento deben tener calificaciones crediticias similares, para filtrar el efecto de los diferenciales de rendimiento causados por el riesgo crediticio. [5] Por esta razón, muchos operadores observan de cerca la curva de rendimiento de los títulos de deuda del Tesoro de EE. UU. , que se consideran libres de riesgo. Informalmente llamada "curva de rendimiento del Tesoro", generalmente se traza en un gráfico como el de la derecha. [6] Las descripciones matemáticas más formales de esta relación a menudo se denominan estructura temporal de las tasas de interés .

Las curvas de rendimiento suelen tener una pendiente ascendente asintótica : cuanto más largo es el vencimiento, mayor es el rendimiento, con aumentos marginales decrecientes (es decir, a medida que uno se mueve hacia la derecha, la curva se aplana). Según The Economist , la pendiente de la curva de rendimiento se puede medir por la diferencia, o "spread", entre los rendimientos de los bonos del Tesoro de Estados Unidos a dos y diez años . Un spread más amplio indica una pendiente más pronunciada. [7]
Existen dos explicaciones comunes para las curvas de rendimiento con pendiente ascendente. En primer lugar, puede ser que el mercado esté anticipando un aumento en la tasa libre de riesgo . Si los inversores se abstienen de invertir ahora, pueden recibir una mejor tasa en el futuro. Por lo tanto, según la teoría de precios de arbitraje , los inversores que están dispuestos a bloquear su dinero ahora necesitan ser compensados por el aumento previsto en las tasas, de ahí la mayor tasa de interés en las inversiones a largo plazo. Otra explicación es que los vencimientos más largos implican mayores riesgos para el inversor (es decir, el prestamista). El mercado necesita una prima de riesgo , ya que a duraciones más largas hay más incertidumbre y una mayor probabilidad de eventos que afecten a la inversión. Esta explicación depende de la noción de que la economía enfrenta más incertidumbres en el futuro lejano que en el corto plazo. Este efecto se conoce como el diferencial de liquidez. Si el mercado espera más volatilidad en el futuro, incluso si se anticipa que las tasas de interés disminuirán, el aumento de la prima de riesgo puede influir en el diferencial y causar un aumento del rendimiento.
También puede darse la situación opuesta, en la que la curva de rendimientos se "invierte", con tasas de interés a corto plazo más altas que las de largo plazo. Por ejemplo, en noviembre de 2004, la curva de rendimientos de los bonos del gobierno del Reino Unido se invirtió parcialmente. El rendimiento del bono a 10 años se situó en el 4,68%, pero fue sólo del 4,45% para el bono a 30 años. La anticipación del mercado de una caída de las tasas de interés causa tales incidentes. También pueden existir primas de liquidez negativas si los inversores a largo plazo dominan el mercado, pero la opinión predominante es que predomina una prima de liquidez positiva, por lo que sólo la anticipación de una caída de las tasas de interés causará una curva de rendimientos invertida. Las curvas de rendimientos fuertemente invertidas han precedido históricamente a las recesiones económicas.
La forma de la curva de rendimiento está influenciada por la oferta y la demanda : por ejemplo, si hay una gran demanda de bonos a largo plazo, por ejemplo de los fondos de pensiones para igualar sus obligaciones fijas con los jubilados, y no hay suficientes bonos en existencia para satisfacer esta demanda, entonces se puede esperar que los rendimientos de los bonos a largo plazo sean bajos, independientemente de las opiniones de los participantes del mercado sobre los eventos futuros.
La curva de rendimiento también puede ser plana o tener forma de joroba, debido a que las tasas de interés anticipadas se mantendrán estables o la volatilidad de corto plazo superará a la volatilidad de largo plazo.
Las curvas de rendimiento se mueven continuamente durante todo el tiempo que los mercados están abiertos, lo que refleja la reacción del mercado a las noticias. Otro " hecho estilizado " es que las curvas de rendimiento tienden a moverse en paralelo; es decir, la curva de rendimiento se desplaza hacia arriba y hacia abajo a medida que los niveles de las tasas de interés suben y bajan, lo que se denomina "desplazamiento paralelo".
No existe una única curva de rendimiento que describa el coste del dinero para todo el mundo. El factor más importante para determinar una curva de rendimiento es la moneda en la que están denominados los valores. La posición económica de los países y las empresas que utilizan cada moneda es un factor primordial para determinar la curva de rendimiento. Las distintas instituciones piden dinero prestado a diferentes tipos de interés, en función de su solvencia .
Las curvas de rendimiento correspondientes a los bonos emitidos por los gobiernos en su propia moneda se denominan curva de rendimiento de los bonos gubernamentales (curva gubernamental). Los bancos con calificaciones crediticias altas (Aa/AA o superiores) se prestan dinero entre sí a las tasas LIBOR . Estas curvas de rendimiento suelen ser un poco más altas que las curvas gubernamentales. Son las más importantes y las más utilizadas en los mercados financieros y se conocen como curva LIBOR o curva swap . La construcción de la curva swap se describe a continuación.
Además de la curva gubernamental y la curva LIBOR, existen curvas corporativas (de empresas). Estas se construyen a partir de los rendimientos de los bonos emitidos por corporaciones. Dado que las corporaciones tienen menor solvencia crediticia que la mayoría de los gobiernos y la mayoría de los grandes bancos, estos rendimientos suelen ser más altos. Las curvas de rendimiento corporativas suelen cotizarse en términos de un "diferencial de crédito" sobre la curva de swaps pertinente. Por ejemplo, el punto de la curva de rendimiento a cinco años para Vodafone podría cotizarse como LIBOR + 0,25%, donde 0,25% (a menudo escrito como 25 puntos básicos o 25 pb) es el diferencial de crédito.

Desde la era posterior a la Gran Depresión hasta el presente, la curva de rendimiento ha sido generalmente "normal", lo que significa que los rendimientos aumentan a medida que se alarga el vencimiento (es decir, la pendiente de la curva de rendimiento es positiva). Esta pendiente positiva refleja las expectativas de los inversores de que la economía crezca en el futuro y, lo que es más importante, de que este crecimiento esté asociado con una mayor expectativa de que la inflación aumentará en el futuro en lugar de disminuir. Esta expectativa de una mayor inflación conduce a expectativas de que el banco central endurezca la política monetaria elevando las tasas de interés a corto plazo en el futuro para desacelerar el crecimiento económico y amortiguar la presión inflacionaria. También crea una necesidad de una prima de riesgo asociada con la incertidumbre sobre la futura tasa de inflación y el riesgo que esto supone para el valor futuro de los flujos de efectivo. Los inversores incorporan estos riesgos en la curva de rendimiento al exigir rendimientos más altos para vencimientos más lejanos en el futuro. En una curva de rendimiento con pendiente positiva, los prestamistas se benefician del paso del tiempo, ya que los rendimientos disminuyen a medida que los bonos se acercan al vencimiento (a medida que disminuye el rendimiento, el precio aumenta ); Esto se conoce como "rolldown" y es un componente significativo de las ganancias en la inversión en renta fija (es decir, comprar y vender, no necesariamente mantener hasta el vencimiento), particularmente si la inversión está apalancada . [8]
Sin embargo, una curva de rendimiento con pendiente positiva no siempre ha sido la norma. Durante gran parte del siglo XIX y principios del XX, la economía estadounidense experimentó un crecimiento tendencial con deflación persistente , no inflación. Durante este período, la curva de rendimiento generalmente estaba invertida, lo que reflejaba el hecho de que la deflación hacía que los flujos de efectivo actuales fueran menos valiosos que los flujos de efectivo futuros. Durante este período de deflación persistente, una curva de rendimiento "normal" tenía pendiente negativa.
Históricamente, el rendimiento de los bonos del Tesoro a 20 años ha sido, en promedio, aproximadamente dos puntos porcentuales superior al de las letras del Tesoro a tres meses. En situaciones en las que esta brecha aumenta (por ejemplo, el rendimiento del bono del Tesoro a 20 años aumenta mucho más que el rendimiento del bono del Tesoro a tres meses), se espera que la economía mejore rápidamente en el futuro. Este tipo de curva se puede ver al comienzo de una expansión económica (o después del final de una recesión). En estos casos, el estancamiento económico habrá deprimido las tasas de interés a corto plazo; sin embargo, las tasas comienzan a aumentar una vez que la demanda de capital se restablece mediante el crecimiento de la actividad económica.
En enero de 2010, la brecha entre los rendimientos de los bonos del Tesoro a dos años y a diez años se amplió a 2,92 puntos porcentuales, su nivel más alto hasta la fecha.
Una curva de rendimiento plana se observa cuando todos los vencimientos tienen rendimientos similares, mientras que una curva con joroba se produce cuando los rendimientos a corto y largo plazo son iguales y los rendimientos a medio plazo son más altos que los de corto y largo plazo. Una curva plana envía señales de incertidumbre en la economía. Esta señal mixta puede revertirse a una curva normal o podría convertirse más tarde en una curva invertida. No se puede explicar con la teoría del mercado segmentado que se analiza a continuación.


En circunstancias excepcionales, los inversores se conformarán con rendimientos más bajos asociados a la deuda a largo plazo de bajo riesgo si creen que la economía entrará en recesión en el futuro cercano. Por ejemplo, el S&P 500 experimentó una caída drástica a mediados de 2007, de la que se recuperó por completo a principios de 2013. Los inversores que habían comprado bonos del Tesoro a 10 años en 2006 habrían recibido un rendimiento seguro y estable hasta 2015, posiblemente logrando mejores retornos que quienes invirtieron en acciones durante ese período volátil.
La tesis doctoral de 1986 del economista Campbell Harvey [9] demostró que una curva de rendimiento invertida pronostica con precisión las recesiones en Estados Unidos. Una curva invertida ha indicado un empeoramiento de la situación económica en el futuro ocho veces desde 1970. [10]
Además de ser una señal potencial de una caída económica, las curvas de rendimiento invertidas también implican que el mercado cree que la inflación se mantendrá baja. Esto se debe a que, incluso si hay una recesión, un rendimiento bajo de los bonos se verá compensado por una baja inflación. Sin embargo, factores técnicos, como una huida hacia la calidad o situaciones económicas o monetarias globales, pueden causar un aumento en la demanda de bonos en el extremo largo de la curva de rendimiento, lo que hace que los tipos a largo plazo caigan. La caída de los tipos a largo plazo en presencia de tasas a corto plazo en aumento se conoce como "el enigma de Greenspan". [11]
La pendiente de la curva de rendimiento es uno de los predictores más poderosos del crecimiento económico futuro, la inflación y las recesiones. [12] [13] Una medida de la pendiente de la curva de rendimiento (es decir, la diferencia entre la tasa de los bonos del Tesoro a 10 años y la tasa de los bonos del Tesoro a 3 meses) está incluida en el Índice de estrés financiero publicado por la Reserva Federal de St. Louis . [14] Una medida diferente de la pendiente (es decir, la diferencia entre las tasas de los bonos del Tesoro a 10 años y la tasa de los fondos federales ) está incorporada en el Índice de indicadores económicos líderes publicado por The Conference Board . [15]
Una curva de rendimiento invertida es a menudo un presagio de recesión . Una curva de rendimiento con pendiente positiva es a menudo un presagio de crecimiento inflacionario . El trabajo de Arturo Estrella y Tobias Adrian ha establecido el poder predictivo de una curva de rendimiento invertida para señalar una recesión. Sus modelos muestran que cuando la diferencia entre las tasas de interés a corto plazo (utilizan letras del Tesoro a 3 meses) y las tasas de interés a largo plazo (bonos del Tesoro a 10 años) al final de un ciclo de ajuste de la reserva federal es negativa o menos de 93 puntos básicos positivos, generalmente se produce un aumento del desempleo. [16] La Reserva Federal de Nueva York publica una predicción mensual de probabilidad de recesión derivada de la curva de rendimiento y basada en el trabajo de Estrella.
Todas las recesiones en los EE. UU. desde 1970 han sido precedidas por una curva de rendimiento invertida (10 años frente a 3 meses). Durante el mismo período, cada aparición de una curva de rendimiento invertida ha sido seguida por una recesión, según lo declarado por el comité de datación del ciclo económico de la NBER . [17] La curva de rendimiento se invirtió en la primera mitad de 2019, por primera vez desde 2007. [18] [19] [20]
Estrella y otros han postulado que la curva de rendimiento afecta el ciclo económico a través del balance de los bancos (o instituciones financieras similares a los bancos ). [21] Cuando la curva de rendimiento se invierte, los bancos a menudo se ven atrapados pagando más por depósitos a corto plazo (u otras formas de financiación mayorista a corto plazo) de lo que están ganando por nuevos préstamos a largo plazo, lo que lleva a una pérdida de rentabilidad y renuencia a prestar, lo que resulta en una crisis crediticia . Cuando la curva de rendimiento tiene pendiente ascendente, los bancos pueden tomar depósitos a corto plazo de manera rentable y hacer nuevos préstamos a largo plazo, por lo que están ansiosos por proporcionar crédito a los prestatarios. Esto eventualmente conduce a una burbuja crediticia .
Existen tres teorías económicas principales que intentan explicar cómo varían los rendimientos con el vencimiento. Dos de ellas son posiciones extremas, mientras que la tercera intenta encontrar un punto intermedio entre las dos anteriores.
Esta hipótesis supone que los distintos vencimientos son sustitutos perfectos y sugiere que la forma de la curva de rendimiento depende de las expectativas de los participantes del mercado sobre las tasas de interés futuras. Supone que las fuerzas del mercado harán que las tasas de interés de los distintos plazos de los bonos sean tales que el valor final esperado de una secuencia de inversiones a corto plazo será igual al valor final conocido de una única inversión a largo plazo. Si esto no fuera así, la teoría supone que los inversores demandarían rápidamente más bonos a corto o largo plazo actuales (el que dé el mayor rendimiento esperado a largo plazo), y esto reduciría el rendimiento de los bonos actuales de ese plazo y aumentaría el rendimiento de los bonos actuales del otro plazo, de modo que rápidamente se cumpliría la supuesta igualdad de rendimientos esperados de los dos enfoques de inversión.
Con esto, los tipos de interés de futuros , junto con el supuesto de que las oportunidades de arbitraje serán mínimas en los mercados de futuros y de que los tipos de interés de futuros son estimaciones imparciales de los tipos de interés spot futuros, proporcionan suficiente información para construir una curva de rendimiento esperado completa. Por ejemplo, si los inversores tienen una expectativa de lo que serán los tipos de interés a 1 año el año que viene, el tipo de interés actual a 2 años se puede calcular como la capitalización del tipo de interés a 1 año de este año por el tipo de interés a 1 año esperado para el año que viene. En términos más generales, se supone que los rendimientos (1+rendimiento) de un instrumento a largo plazo son iguales a la media geométrica de los rendimientos esperados de una serie de instrumentos a corto plazo:
donde i st e i lt son las tasas de interés esperadas a corto plazo y las tasas de interés reales a largo plazo (pero es la tasa de interés real observada a corto plazo para el primer año).
Esta teoría es coherente con la observación de que los rendimientos suelen fluctuar al unísono, pero no explica la persistencia de la forma de la curva de rendimientos.
Una de las deficiencias de la teoría de las expectativas es que no tiene en cuenta el riesgo de tipo de interés inherente a la inversión en bonos.
La teoría de la prima de liquidez es una derivación de la teoría de las expectativas puras. La teoría de la prima de liquidez afirma que los tipos de interés a largo plazo no sólo reflejan las suposiciones de los inversores sobre los tipos de interés futuros, sino que también incluyen una prima por mantener bonos a largo plazo (los inversores prefieren bonos a corto plazo a bonos a largo plazo), llamada prima de plazo o prima de liquidez. Esta prima compensa a los inversores por el riesgo añadido de tener su dinero atado durante un periodo más largo, incluida la mayor incertidumbre de los precios. Debido a la prima de plazo, los rendimientos de los bonos a largo plazo tienden a ser más altos que los rendimientos a corto plazo y la curva de rendimiento tiene pendiente ascendente. Los rendimientos a largo plazo también son más altos no sólo por la prima de liquidez, sino también por la prima de riesgo añadida por el riesgo de impago de mantener un título a largo plazo. La hipótesis de las expectativas del mercado se combina con la teoría de la prima de liquidez:
¿Dónde está la prima de riesgo asociada a un bono de un año?
La teoría del hábitat preferido es una variante de la teoría de la prima de liquidez y establece que, además de las expectativas sobre las tasas de interés, los inversores tienen horizontes de inversión distintos y requieren una prima significativa para comprar bonos con vencimientos fuera de su vencimiento o hábitat "preferido". Los defensores de esta teoría creen que los inversores a corto plazo son más frecuentes en el mercado de renta fija y, por lo tanto, las tasas a largo plazo tienden a ser más altas que las tasas a corto plazo, en su mayor parte, pero las tasas a corto plazo pueden ser más altas que las tasas a largo plazo ocasionalmente. Esta teoría es coherente tanto con la persistencia de la forma normal de la curva de rendimiento como con la tendencia de la curva de rendimiento a subir y bajar manteniendo su forma.
Esta teoría también se denomina hipótesis del mercado segmentado . En esta teoría, los instrumentos financieros de diferentes plazos no son sustituibles . Como resultado, la oferta y la demanda en los mercados de instrumentos a corto y largo plazo se determinan en gran medida de forma independiente. Los posibles inversores deciden de antemano si necesitan instrumentos a corto o largo plazo. Si los inversores prefieren que su cartera sea líquida, preferirán los instrumentos a corto plazo a los instrumentos a largo plazo. Por lo tanto, el mercado de instrumentos a corto plazo recibirá una mayor demanda. Una mayor demanda del instrumento implica precios más altos y un menor rendimiento. Esto explica el hecho estilizado de que los rendimientos a corto plazo suelen ser inferiores a los rendimientos a largo plazo. Esta teoría explica el predominio de la forma normal de la curva de rendimiento. Sin embargo, debido a que la oferta y la demanda de los dos mercados son independientes, esta teoría no explica el hecho observado de que los rendimientos tienden a moverse juntos (es decir, desplazamientos hacia arriba y hacia abajo en la curva).
El 15 de agosto de 1971, el presidente estadounidense Richard Nixon anunció que el dólar estadounidense ya no se basaría en el patrón oro , poniendo así fin al sistema de Bretton Woods e iniciando la era de los tipos de cambio flotantes .
Los tipos de cambio flotantes complicaron la vida a los operadores de bonos, incluidos los de Salomon Brothers en la ciudad de Nueva York . A mediados de los años 70, alentados por el jefe de investigación de bonos de Salomon, Marty Liebowitz, los operadores comenzaron a pensar en los rendimientos de los bonos de nuevas maneras. En lugar de pensar en cada vencimiento (un bono a diez años, uno a cinco años, etc.) como un mercado separado, comenzaron a dibujar una curva a través de todos sus rendimientos. La parte más cercana al momento actual se conoció como el extremo corto ; los rendimientos de los bonos más lejanos se convirtieron, naturalmente, en el extremo largo .
Los académicos tuvieron que ponerse al día con los profesionales en esta materia. Un desarrollo teórico importante provino de un matemático checo, Oldrich Vasicek , quien sostuvo en un artículo de 1977 que los precios de los bonos a lo largo de la curva están impulsados por el extremo corto (según la medida martingala equivalente neutral al riesgo) y, en consecuencia, por las tasas de interés a corto plazo. El modelo matemático para el trabajo de Vasicek fue dado por un proceso de Ornstein-Uhlenbeck , pero desde entonces ha sido desacreditado porque el modelo predice una probabilidad positiva de que la tasa a corto plazo se vuelva negativa y es inflexible en la creación de curvas de rendimiento de diferentes formas. El modelo de Vasicek ha sido reemplazado por muchos modelos diferentes, incluido el modelo de Hull-White (que permite parámetros que varían con el tiempo en el proceso de Ornstein-Uhlenbeck), el modelo de Cox-Ingersoll-Ross , que es un proceso de Bessel modificado , y el marco de Heath-Jarrow-Morton . También hay muchas modificaciones a cada uno de estos modelos, pero véase el artículo sobre el modelo de tasa a corto plazo . Otro enfoque moderno es el modelo de mercado LIBOR , introducido por Brace, Gatarek y Musiela en 1997 y desarrollado por otros posteriormente. En 1996, un grupo de operadores de derivados liderados por Olivier Doria (entonces jefe de swaps en Deutsche Bank) y Michele Faissola, contribuyeron a una extensión de las curvas de rendimiento de swaps en todas las principales monedas europeas. Hasta entonces, el mercado daría precios hasta vencimientos de 15 años. El equipo extendió el vencimiento de las curvas de rendimiento europeas hasta 50 años (para la lira, el franco francés, el marco alemán, la corona danesa y muchas otras monedas, incluido el ecu). Esta innovación fue una importante contribución a la emisión de bonos cupón cero a largo plazo y la creación de hipotecas a largo plazo.
La representación habitual de la curva de rendimiento se realiza en términos de una función P, definida para todos los tiempos futuros t , de modo que P( t ) representa el valor actual de recibir una unidad de moneda dentro de t años. Si P se define para todos los tiempos futuros t , entonces podemos recuperar fácilmente el rendimiento (es decir, la tasa de interés anualizada) por tomar dinero prestado durante ese período de tiempo mediante la fórmula
Por lo tanto, la dificultad principal a la hora de definir una curva de rendimiento es determinar la función P( t ). P se denomina función del factor de descuento o función del bono cupón cero.
Las curvas de rendimiento se construyen a partir de los precios disponibles en el mercado de bonos o en el mercado monetario . Mientras que las curvas de rendimiento construidas a partir del mercado de bonos utilizan solo los precios de una clase específica de bonos (por ejemplo, los bonos emitidos por el gobierno del Reino Unido), las curvas de rendimiento construidas a partir del mercado monetario utilizan los precios del "efectivo" de las tasas LIBOR de hoy, que determinan el "extremo corto" de la curva, es decir, para t ≤ 3m, los futuros de tasas de interés que determinan la sección media de la curva (3m ≤ t ≤ 15m) y los swaps de tasas de interés que determinan el "extremo largo" (1y ≤ t ≤ 60y).
El ejemplo que se da en la tabla de la derecha se conoce como curva LIBOR porque se construye utilizando tasas LIBOR o tasas swap . Una curva LIBOR es la curva de tasa de interés más utilizada, ya que representa el valor crediticio de las entidades privadas con una calificación A+, aproximadamente el equivalente a los bancos comerciales. Si uno sustituye las tasas LIBOR y swap por los rendimientos de los bonos del gobierno, se llega a lo que se conoce como una curva gubernamental, generalmente considerada la curva de tasa de interés libre de riesgo para la moneda subyacente. El diferencial entre la tasa LIBOR (o swap) y el rendimiento de los bonos del gobierno de vencimiento similar suele ser positivo, lo que significa que el endeudamiento privado tiene una prima sobre el endeudamiento gubernamental. Este diferencial es una medida de la diferencia en las tolerancias de riesgo de los prestamistas a los dos tipos de endeudamiento. Para el mercado estadounidense, un punto de referencia común para dicho diferencial es el denominado diferencial TED .
En cualquier caso, los datos de mercado disponibles proporcionan una matriz A de flujos de efectivo, en la que cada fila representa un instrumento financiero particular y cada columna representa un punto en el tiempo. El elemento ( i , j )-ésimo de la matriz representa la cantidad que el instrumento i pagará el día j . Sea el vector F el precio actual del instrumento (de modo que el i -ésimo instrumento tenga valor F ( i )), entonces, por definición de nuestra función de factor de descuento P, deberíamos tener que F = AP (esta es una multiplicación de matrices). En realidad, el ruido en los mercados financieros significa que no es posible encontrar una P que resuelva esta ecuación exactamente, y nuestro objetivo es encontrar un vector P tal que
donde es el vector más pequeño posible (donde el tamaño de un vector podría medirse tomando su norma , por ejemplo).
Incluso si podemos resolver esta ecuación, solo habremos determinado P ( t ) para aquellos t que tienen un flujo de efectivo proveniente de uno o más de los instrumentos originales a partir de los cuales estamos creando la curva. Los valores para otros t se determinan normalmente utilizando algún tipo de esquema de interpolación .
Los profesionales e investigadores han sugerido muchas maneras de resolver la ecuación A*P = F. Resulta que el método más natural –el de minimizar mediante regresión de mínimos cuadrados– conduce a resultados insatisfactorios. La gran cantidad de ceros en la matriz A significa que la función P resulta ser “irregular”.
En su exhaustivo libro sobre modelos de tipos de interés, James y Webber señalan que se han sugerido las siguientes técnicas para resolver el problema de encontrar P:
En el mercado monetario, los profesionales pueden utilizar diferentes técnicas para calcular distintas áreas de la curva. Por ejemplo, en el extremo corto de la curva, donde hay pocos flujos de efectivo, los primeros elementos de P pueden hallarse haciendo un bootstrap de uno a otro. En el extremo largo, se puede utilizar una técnica de regresión con una función de costo que valore la suavidad.
El análisis de los valores de los bonos tiene una dimensión temporal. Un bono a 10 años en el momento de la compra se convierte en un bono a 9 años un año después, y el año siguiente se convierte en un bono a 8 años, etc. Cada año, el bono se acerca cada vez más a su vencimiento, lo que da como resultado una menor volatilidad y una duración más corta y exige una tasa de interés más baja cuando la curva de rendimiento está subiendo. Como la caída de las tasas crea precios en aumento, el valor de un bono aumentará inicialmente a medida que las tasas más bajas del vencimiento más corto se conviertan en su nueva tasa de mercado. Debido a que un bono siempre está anclado por su vencimiento final, el precio en algún momento debe cambiar de dirección y caer al valor nominal en el momento del reembolso.
Se puede calcular el valor de mercado de un bono en diferentes momentos de su vida. Cuando la curva de rendimiento es pronunciada, se predice que el bono tendrá una gran ganancia de capital en los primeros años antes de caer en precio más adelante. Cuando la curva de rendimiento es plana, se predice que la ganancia de capital será mucho menor y hay poca variabilidad en los rendimientos totales del bono a lo largo del tiempo.
A medida que los tipos de interés del mercado aumentan o disminuyen, el impacto rara vez es el mismo en cada punto de la curva de rendimiento, es decir, la curva rara vez se mueve hacia arriba o hacia abajo en paralelo. Debido a que los bonos a largo plazo tienen una mayor duración, un aumento de los tipos provocará una mayor pérdida de capital para ellos que para los bonos a corto plazo. Pero casi siempre, el tipo de vencimiento a largo plazo cambiará mucho menos, aplanando la curva de rendimiento. El mayor cambio de los tipos en el extremo corto compensará en cierta medida la ventaja proporcionada por la menor duración del bono a corto plazo.
Los bonos de larga duración tienden a tener una reversión a la media, lo que significa que tienden fácilmente a una media de largo plazo. La parte media de la curva (5-10 años) registrará la mayor ganancia porcentual en los rendimientos si se prevé una inflación, incluso si las tasas de interés no han cambiado. El extremo largo no se mueve tanto en términos porcentuales debido a las propiedades de reversión a la media.
El 'rendimiento total' anual del bono es a) la suma del rendimiento del cupón más b) la ganancia de capital proveniente del cambio de valoración a medida que se desliza hacia abajo en la curva de rendimiento y c) cualquier ganancia o pérdida de capital proveniente del cambio en las tasas de interés en ese punto en la curva de rendimiento. [23]
1. ^ El modelo de predicción de la recesión de la Reserva Federal de Nueva York utiliza el rendimiento promedio mensual a 10 años frente al rendimiento equivalente de bonos a 3 meses para calcular el diferencial de plazo. Por lo tanto, las inversiones intradía y diarias no cuentan como inversiones a menos que conduzcan a una inversión sobre una base promedio mensual. En diciembre de 2018, partes de la curva de rendimiento se invirtieron por primera vez desde la recesión de 2008-2009 . [24] Sin embargo, la parte de 10 años frente a 3 meses no se invirtió hasta el 22 de marzo de 2019 y volvió a una pendiente positiva el 1 de abril de 2019 (es decir, solo 8 días después). [25] [26] El promedio mensual de la diferencia entre 10 años y 3 meses (rendimiento equivalente de bonos) alcanzó cero puntos básicos en mayo de 2019. Tanto marzo como abril de 2019 tuvieron diferenciales promedio mensuales mayores a cero puntos básicos a pesar de las inversiones intradía y diarias en marzo y abril. Por lo tanto, la tabla muestra la inversión de 2019 a partir de mayo de 2019. Asimismo, las inversiones diarias de septiembre de 1998 no resultaron en diferenciales de plazo negativos en promedio mensual y, por lo tanto, no constituyen una falsa alarma.
2. ^ El modelo de predicción de la recesión estipuló que la recesión comenzó en febrero de 2020, un mes antes de que la Organización Mundial de la Salud declarara al COVID-19 una pandemia.
{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace ){{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace )