Un oscilador de cristal es un circuito oscilador electrónico que utiliza un cristal piezoeléctrico como elemento selectivo de frecuencia . [1] [2] [3] La frecuencia del oscilador se utiliza a menudo para realizar un seguimiento del tiempo, como en los relojes de pulsera de cuarzo , para proporcionar una señal de reloj estable para circuitos integrados digitales y para estabilizar frecuencias para transmisores y receptores de radio . El tipo más común de resonador piezoeléctrico utilizado es un cristal de cuarzo , por lo que los circuitos osciladores que los incorporan se conocieron como osciladores de cristal. [1] Sin embargo, otros materiales piezoeléctricos, incluida la cerámica policristalina , se utilizan en circuitos similares.
Un oscilador de cristal se basa en el ligero cambio de forma de un cristal de cuarzo bajo un campo eléctrico , una propiedad conocida como piezoelectricidad inversa . Un voltaje aplicado a los electrodos del cristal hace que cambie de forma; cuando se elimina el voltaje, el cristal genera un pequeño voltaje a medida que vuelve elásticamente a su forma original. El cuarzo oscila a una frecuencia de resonancia estable, comportándose como un circuito RLC , pero con un factor Q mucho más alto (menor pérdida de energía en cada ciclo de oscilación). Una vez que un cristal de cuarzo se ajusta a una frecuencia particular (que se ve afectada por la masa de los electrodos unidos al cristal, la orientación del cristal, la temperatura y otros factores), mantiene esa frecuencia con alta estabilidad. [4]
Los cristales de cuarzo se fabrican para frecuencias que van desde unas pocas decenas de kilohercios hasta cientos de megahercios. En 2003, se fabricaban anualmente alrededor de dos mil millones de cristales. [5] La mayoría se utilizan para dispositivos de consumo como relojes de pulsera , relojes de pared , radios , ordenadores y teléfonos móviles . Sin embargo, en aplicaciones en las que se necesita un tamaño y un peso pequeños, los cristales se pueden sustituir por resonadores acústicos de película fina , especialmente si se necesita una resonancia de frecuencia ultraalta (más de aproximadamente 1,5 GHz). Los cristales de cuarzo también se encuentran en el interior de equipos de prueba y medición, como contadores, generadores de señales y osciloscopios .

Un oscilador de cristal es un circuito de tipo oscilador eléctrico que utiliza un resonador piezoeléctrico, un cristal, como elemento determinante de la frecuencia. Cristal es el término común utilizado en electrónica para el componente determinante de la frecuencia, una oblea de cristal de cuarzo o cerámica con electrodos conectados a ella. Un término más preciso para "cristal" es resonador piezoeléctrico . Los cristales también se utilizan en otros tipos de circuitos electrónicos, como los filtros de cristal .
Los resonadores piezoeléctricos se venden como componentes separados para su uso en circuitos de osciladores de cristal. También suelen incorporarse en un único paquete con el circuito de osciladores de cristal.


La piezoelectricidad fue descubierta por Jacques y Pierre Curie en 1880. Paul Langevin fue el primero en investigar los resonadores de cuarzo para su uso en sonares durante la Primera Guerra Mundial. El primer oscilador controlado por cristal , que utilizaba un cristal de sal de Rochelle , fue construido en 1917 y patentado [6] en 1918 por Alexander M. Nicholson en Bell Telephone Laboratories , aunque su prioridad fue disputada por Walter Guyton Cady . [7] Cady construyó el primer oscilador de cristal de cuarzo en 1921. [8] Otros innovadores tempranos en osciladores de cristal de cuarzo incluyen a GW Pierce y Louis Essen .
Los osciladores de cristal de cuarzo se desarrollaron para referencias de frecuencia de alta estabilidad durante las décadas de 1920 y 1930. Antes de los cristales, las estaciones de radio controlaban su frecuencia con circuitos sintonizados , que podían desviarse fácilmente de la frecuencia en 3-4 kHz. [9] Dado que a las estaciones de transmisión se les asignaban frecuencias con una diferencia de solo 10 kHz (América) o 9 kHz (en otros lugares), la interferencia entre estaciones adyacentes debido a la deriva de frecuencia era un problema común. [9] En 1925, Westinghouse instaló un oscilador de cristal en su estación insignia KDKA, [9] y en 1926, los cristales de cuarzo se usaban para controlar la frecuencia de muchas estaciones de transmisión y eran populares entre los operadores de radioaficionados. [10] En 1928, Warren Marrison de Bell Laboratories desarrolló el primer reloj de cristal de cuarzo . Con precisiones de hasta 1 segundo en 30 años (30 ms/año, o 0,95 ns/s), [8] los relojes de cuarzo reemplazaron a los relojes de péndulo de precisión como los cronometradores más precisos del mundo hasta que se desarrollaron los relojes atómicos en la década de 1950. Utilizando el trabajo inicial de Bell Laboratories, American Telephone and Telegraph Company (AT&T) finalmente estableció su división Frequency Control Products, que luego se escindió y se conoce hoy como Vectron International. [11]
Varias empresas comenzaron a producir cristales de cuarzo para uso electrónico durante esta época. Utilizando lo que ahora se consideran métodos primitivos, se produjeron alrededor de 100.000 unidades de cristal en los Estados Unidos durante 1939. Durante la Segunda Guerra Mundial , los cristales se fabricaron a partir de cristal de cuarzo natural, prácticamente todos procedentes de Brasil . La escasez de cristales durante la guerra causada por la demanda de un control preciso de la frecuencia de las radios y radares militares y navales estimuló la investigación de posguerra sobre el cultivo de cuarzo sintético, y en 1950 se desarrolló un proceso hidrotermal para el cultivo de cristales de cuarzo a escala comercial en los Laboratorios Bell. En la década de 1970, prácticamente todos los cristales utilizados en electrónica eran sintéticos.
En 1968, Juergen Staudte inventó un proceso fotolitográfico para fabricar osciladores de cristal de cuarzo mientras trabajaba en North American Aviation (ahora Rockwell ) que permitió hacerlos lo suficientemente pequeños para productos portátiles como relojes. [12]
Aunque los osciladores de cristal todavía utilizan habitualmente cristales de cuarzo, cada vez son más comunes los dispositivos que utilizan otros materiales, como los resonadores cerámicos .
Un cristal es un sólido en el que los átomos , moléculas o iones constituyentes están agrupados en un patrón ordenado regularmente y repetitivo que se extiende en las tres dimensiones espaciales.
Casi cualquier objeto hecho de un material elástico podría usarse como un cristal, con transductores apropiados , ya que todos los objetos tienen frecuencias resonantes naturales de vibración . Por ejemplo, el acero es muy elástico y tiene una alta velocidad del sonido. Se usaba a menudo en filtros mecánicos antes del cuarzo. La frecuencia de resonancia depende del tamaño, la forma, la elasticidad y la velocidad del sonido en el material. Los cristales de alta frecuencia generalmente se cortan en forma de un simple rectángulo o disco circular. Los cristales de baja frecuencia, como los que se usan en los relojes digitales, generalmente se cortan en forma de diapasón . Para aplicaciones que no necesitan una sincronización muy precisa, a menudo se usa un resonador cerámico de bajo costo en lugar de un cristal de cuarzo.
Cuando un cristal de cuarzo se corta y se monta correctamente, se puede hacer que se deforme en un campo eléctrico aplicando un voltaje a un electrodo cerca o sobre el cristal. Esta propiedad se conoce como piezoelectricidad inversa . Cuando se elimina el campo, el cuarzo genera un campo eléctrico al volver a su forma anterior, y esto puede generar un voltaje. El resultado es que un cristal de cuarzo se comporta como un circuito RLC , compuesto por un inductor , un condensador y una resistencia , con una frecuencia de resonancia precisa.
El cuarzo tiene la ventaja adicional de que sus constantes elásticas y su tamaño cambian de tal manera que la dependencia de la frecuencia con la temperatura puede ser muy baja. Las características específicas dependen del modo de vibración y del ángulo en el que se corta el cuarzo (en relación con sus ejes cristalográficos). [13] Por lo tanto, la frecuencia de resonancia de la placa, que depende de su tamaño, no cambia mucho. Esto significa que un reloj, filtro u oscilador de cuarzo sigue siendo preciso. Para aplicaciones críticas, el oscilador de cuarzo se monta en un contenedor con temperatura controlada, llamado horno de cristal , y también se puede montar sobre amortiguadores para evitar perturbaciones por vibraciones mecánicas externas.
Un cristal de cuarzo se puede modelar como una red eléctrica con puntos de resonancia de baja impedancia (serie) y alta impedancia (paralelo) espaciados muy cerca entre sí. Matemáticamente, utilizando la transformada de Laplace , la impedancia de esta red se puede escribir como:

o
donde es la frecuencia compleja ( ), es la frecuencia angular resonante en serie y es la frecuencia angular resonante en paralelo.
Añadir capacitancia a través de un cristal hace que la frecuencia de resonancia (paralela) disminuya. Añadir inductancia a través de un cristal hace que la frecuencia de resonancia (paralela) aumente. Estos efectos se pueden utilizar para ajustar la frecuencia a la que oscila un cristal. Los fabricantes de cristales normalmente cortan y recortan sus cristales para tener una frecuencia de resonancia específica con una capacitancia de "carga" conocida añadida al cristal. Por ejemplo, un cristal destinado a una carga de 6 pF tiene su frecuencia de resonancia paralela especificada cuando se coloca un condensador de 6,0 pF a través de él. Sin la capacitancia de carga, la frecuencia de resonancia es más alta.
Un cristal de cuarzo proporciona resonancia en serie y en paralelo. La resonancia en serie es unos pocos kilohercios más baja que la resonancia en paralelo. Los cristales por debajo de los 30 MHz generalmente funcionan entre resonancia en serie y en paralelo, lo que significa que el cristal aparece como una reactancia inductiva en funcionamiento, y esta inductancia forma un circuito resonante en paralelo con una capacitancia en paralelo conectada externamente.

Cualquier pequeña capacitancia adicional en paralelo con el cristal hace que la frecuencia baje. Además, la reactancia inductiva efectiva del cristal se puede reducir añadiendo un condensador en serie con el cristal. Esta última técnica puede proporcionar un método útil para recortar la frecuencia oscilatoria dentro de un rango estrecho; en este caso, insertar un condensador en serie con el cristal aumenta la frecuencia de oscilación. Para que un cristal funcione a su frecuencia especificada, el circuito electrónico tiene que ser exactamente el especificado por el fabricante del cristal. Tenga en cuenta que estos puntos implican una sutileza en relación con los osciladores de cristal en este rango de frecuencia: el cristal no suele oscilar exactamente en ninguna de sus frecuencias de resonancia.
Los cristales de más de 30 MHz (hasta >200 MHz) se utilizan generalmente en resonancia en serie, donde la impedancia aparece en su mínimo e igual a la resistencia en serie. Para estos cristales se especifica la resistencia en serie (<100 Ω) en lugar de la capacitancia en paralelo. Para alcanzar frecuencias más altas, se puede hacer vibrar un cristal en uno de sus modos de sobretono , que se producen cerca de múltiplos de la frecuencia de resonancia fundamental. Solo se utilizan sobretonos de número impar. A este tipo de cristal se lo denomina cristal de sobretono 3.º, 5.º o incluso 7.º. Para lograr esto, el circuito oscilador suele incluir circuitos LC adicionales para seleccionar el sobretono deseado.
La característica de frecuencia de un cristal depende de la forma o "corte" del cristal. Un cristal de diapasón se corta generalmente de manera que su dependencia de frecuencia con la temperatura sea cuadrática, con un máximo de alrededor de 25 °C. [ cita requerida ] Esto significa que un oscilador de cristal de diapasón resuena cerca de su frecuencia objetivo a temperatura ambiente, pero se ralentiza cuando la temperatura aumenta o disminuye con respecto a la temperatura ambiente. Un coeficiente parabólico común para un cristal de diapasón de 32 kHz es −0,04 ppm/°C 2 : [ cita requerida ]
En una aplicación real, esto significa que un reloj construido con un cristal de diapasón normal de 32 kHz mantiene la hora correctamente a temperatura ambiente, pero pierde 2 minutos por año a 10 °C por encima o por debajo de la temperatura ambiente y pierde 8 minutos por año a 20 °C por encima o por debajo de la temperatura ambiente debido al cristal de cuarzo.
El circuito oscilador de cristal mantiene la oscilación tomando una señal de voltaje del resonador de cuarzo , amplificándola y enviándola de vuelta al resonador. La tasa de expansión y contracción del cuarzo es la frecuencia resonante y está determinada por el corte y el tamaño del cristal. Cuando la energía de las frecuencias de salida generadas coincide con las pérdidas en el circuito, se puede mantener una oscilación.
Un cristal oscilador tiene dos placas conductoras de electricidad, con una rebanada o diapasón de cristal de cuarzo intercalado entre ellas. Durante el arranque, el circuito de control coloca al cristal en un equilibrio inestable y, debido a la retroalimentación positiva en el sistema, cualquier pequeña fracción de ruido se amplifica, aumentando la oscilación. El resonador de cristal también puede verse como un filtro altamente selectivo de frecuencia en este sistema: solo pasa una subbanda muy estrecha de frecuencias alrededor de la resonante, atenuando todo lo demás. Finalmente, solo la frecuencia resonante está activa. A medida que el oscilador amplifica las señales que salen del cristal, las señales en la banda de frecuencia del cristal se vuelven más fuertes y finalmente dominan la salida del oscilador. La estrecha banda de resonancia del cristal de cuarzo filtra las frecuencias no deseadas.
La frecuencia de salida de un oscilador de cuarzo puede ser la de la resonancia fundamental o la de un múltiplo de dicha resonancia, llamada frecuencia armónica . Los armónicos son un múltiplo entero exacto de la frecuencia fundamental. Pero, como muchos otros resonadores mecánicos, los cristales presentan varios modos de oscilación, normalmente en múltiplos enteros impares de la frecuencia fundamental. Estos se denominan "modos de sobretono" y se pueden diseñar circuitos osciladores para excitarlos. Los modos de sobretono se dan en frecuencias que son múltiplos enteros impares aproximados, pero no exactos, del modo fundamental y, por lo tanto, las frecuencias de sobretono no son armónicos exactos de la fundamental.
Los cristales de alta frecuencia suelen estar diseñados para funcionar en el tercer, quinto o séptimo armónico. Los fabricantes tienen dificultades para producir cristales lo suficientemente finos como para producir frecuencias fundamentales superiores a los 30 MHz. Para producir frecuencias más altas, los fabricantes fabrican cristales de armónicos sintonizados para poner el tercer, quinto o séptimo armónico en la frecuencia deseada, porque son más gruesos y, por lo tanto, más fáciles de fabricar que un cristal fundamental que produciría la misma frecuencia, aunque excitar la frecuencia de armónico deseada requiere un circuito oscilador ligeramente más complicado. [14] [15] [16] [17] [18] Un circuito oscilador de cristal fundamental es más simple y más eficiente y tiene más capacidad de tracción que un circuito de tercer armónico. Dependiendo del fabricante, la frecuencia fundamental más alta disponible puede ser de 25 MHz a 66 MHz. [19] [20]

Una de las principales razones del amplio uso de los osciladores de cristal es su elevado factor Q. Un valor Q típico para un oscilador de cuarzo oscila entre 10 4 y 10 6 , en comparación con quizás 10 2 para un oscilador LC . El Q máximo para un oscilador de cuarzo de alta estabilidad se puede estimar como Q = 1,6 × 10 7 / f , donde f es la frecuencia de resonancia en megahercios. [21] [22]
Una de las características más importantes de los osciladores de cristal de cuarzo es que pueden exhibir un ruido de fase muy bajo . En muchos osciladores, cualquier energía espectral en la frecuencia de resonancia es amplificada por el oscilador, lo que da como resultado una colección de tonos en diferentes fases. En un oscilador de cristal, el cristal vibra principalmente en un eje, por lo tanto, solo una fase es dominante. Esta propiedad de bajo ruido de fase los hace particularmente útiles en telecomunicaciones donde se necesitan señales estables y en equipos científicos donde se necesitan referencias de tiempo muy precisas.
Los cambios ambientales de temperatura, humedad, presión y vibración pueden cambiar la frecuencia de resonancia de un cristal de cuarzo, pero existen varios diseños que reducen estos efectos ambientales. Entre ellos se incluyen el TCXO, el MCXO y el OCXO , que se definen a continuación. Estos diseños, en particular el OCXO, suelen producir dispositivos con una excelente estabilidad a corto plazo. Las limitaciones en la estabilidad a corto plazo se deben principalmente al ruido de los componentes electrónicos en los circuitos del oscilador. La estabilidad a largo plazo está limitada por el envejecimiento del cristal.
Debido al envejecimiento y a factores ambientales (como la temperatura y la vibración), es difícil mantener incluso los mejores osciladores de cuarzo dentro de una fracción en 10 10 de su frecuencia nominal sin un ajuste constante. Por este motivo, los osciladores atómicos se utilizan para aplicaciones que requieren una mayor estabilidad y precisión a largo plazo.

En el caso de cristales que funcionan en resonancia en serie o que se alejan del modo principal mediante la inclusión de un inductor o condensador en serie, pueden experimentarse respuestas espurias significativas (y dependientes de la temperatura). Aunque la mayoría de los modos espurios suelen estar algunas decenas de kilohercios por encima de la resonancia en serie deseada, su coeficiente de temperatura es diferente del modo principal y la respuesta espuria puede pasar por el modo principal a determinadas temperaturas. Incluso si las resistencias en serie en las resonancias espurias parecen más altas que la de la frecuencia deseada, puede producirse un cambio rápido en la resistencia en serie del modo principal a temperaturas específicas cuando las dos frecuencias coinciden. Una consecuencia de estas caídas de actividad es que el oscilador puede bloquearse en una frecuencia espuria a temperaturas específicas. Esto generalmente se minimiza asegurando que el circuito de mantenimiento tenga una ganancia insuficiente para activar los modos no deseados.
También se generan frecuencias espurias al someter el cristal a vibración. Esto modula la frecuencia de resonancia en un pequeño grado por la frecuencia de las vibraciones. Los cristales con corte SC (compensados por tensión) están diseñados para minimizar el efecto de frecuencia de la tensión de montaje y, por lo tanto, son menos sensibles a la vibración. Los efectos de aceleración, incluida la gravedad, también se reducen con los cristales con corte SC, al igual que el cambio de frecuencia con el tiempo debido a la variación de la tensión de montaje a largo plazo. Existen desventajas con los cristales de modo de corte SC, como la necesidad de que el oscilador de mantenimiento discrimine contra otros modos no deseados estrechamente relacionados y un mayor cambio de frecuencia debido a la temperatura cuando se somete a un rango ambiental completo. Los cristales con corte SC son más ventajosos cuando es posible el control de temperatura a su temperatura de coeficiente de temperatura cero (renovación); en estas circunstancias, un rendimiento de estabilidad general de las unidades premium puede acercarse a la estabilidad de los estándares de frecuencia de rubidio.
Los cristales se pueden fabricar para oscilar en un amplio rango de frecuencias, desde unos pocos kilohercios hasta varios cientos de megahercios. Muchas aplicaciones requieren una frecuencia de oscilador de cristal relacionada convenientemente con alguna otra frecuencia deseada, por lo que se fabrican cientos de frecuencias de cristal estándar en grandes cantidades y los distribuidores de productos electrónicos las almacenan. Por ejemplo, los cristales de 3,579545 MHz, que se fabricaron en grandes cantidades para los receptores de televisión en color NTSC , ahora son populares para muchas aplicaciones no televisivas (aunque la mayoría de los receptores de televisión modernos ahora utilizan otros cristales de frecuencia para el decodificador de color). Usando divisores de frecuencia , multiplicadores de frecuencia y circuitos de bucle de enganche de fase , es práctico derivar un amplio rango de frecuencias a partir de una frecuencia de referencia.








El material más común para los cristales osciladores es el cuarzo . Al principio de la tecnología, se utilizaban cristales de cuarzo natural, pero ahora predomina el cuarzo cristalino sintético obtenido por síntesis hidrotermal debido a su mayor pureza, menor coste y manejo más cómodo. Uno de los pocos usos restantes de los cristales naturales es para transductores de presión en pozos profundos. Durante la Segunda Guerra Mundial y durante algún tiempo después, el cuarzo natural fue considerado un material estratégico por los EE. UU. Se importaron cristales grandes de Brasil. Las "lascas" en bruto, el material de origen del cuarzo para la síntesis hidrotermal, se importan a los EE. UU. o se extraen localmente por Coleman Quartz. El valor promedio del cuarzo sintético obtenido en estado natural en 1994 fue de 60 USD /kg. [23]
Existen dos tipos de cristales de cuarzo: levógiros y dextrógiros. Ambos difieren en su rotación óptica , pero son idénticos en otras propiedades físicas. Tanto los cristales levógiros como los dextrógiros se pueden utilizar para osciladores, si el ángulo de corte es correcto. En la fabricación, generalmente se utiliza cuarzo dextrógiro. [24] Los tetraedros de SiO 4 forman hélices paralelas; la dirección de giro de la hélice determina la orientación levógira o dextrógira. Las hélices están alineadas a lo largo del eje c y se fusionan, compartiendo átomos. La masa de las hélices forma una malla de canales pequeños y grandes paralelos al eje c. Los grandes son lo suficientemente grandes como para permitir cierta movilidad de iones y moléculas más pequeños a través del cristal. [25]
El cuarzo existe en varias fases. A 573 °C a 1 atmósfera (y a temperaturas y presiones más altas) el cuarzo α sufre una inversión de cuarzo y se transforma reversiblemente en cuarzo β. Sin embargo, el proceso inverso no es completamente homogéneo y se produce macla de cristales . Se debe tener cuidado durante la fabricación y el procesamiento para evitar la transformación de fase. Otras fases, por ejemplo, las fases de mayor temperatura tridimita y cristobalita , no son significativas para los osciladores. Todos los cristales de osciladores de cuarzo son del tipo cuarzo α.
La espectrofotometría infrarroja se utiliza como uno de los métodos para medir la calidad de los cristales cultivados. Los números de onda 3585, 3500 y 3410 cm −1 se utilizan comúnmente. El valor medido se basa en las bandas de absorción del radical OH y se calcula el valor Q infrarrojo. Los cristales de grado electrónico, grado C, tienen un Q de 1,8 millones o superior; los cristales de grado B premium tienen un Q de 2,2 millones y los cristales de grado A premium especial tienen un Q de 3,0 millones. El valor Q se calcula solo para la región z; los cristales que contienen otras regiones pueden verse afectados negativamente. Otro indicador de calidad es la densidad del canal de grabado; cuando se graba el cristal , se crean canales tubulares a lo largo de defectos lineales. Para el procesamiento que implica grabado, por ejemplo, los cristales de diapasón de reloj de pulsera, es deseable una baja densidad del canal de grabado. La densidad del canal de grabado para el cuarzo barrido es de aproximadamente 10-100 y significativamente más para el cuarzo no barrido. La presencia de canales y picaduras de grabado degrada la Q del resonador e introduce no linealidades. [26]
Los cristales de cuarzo se pueden cultivar para propósitos específicos.
Los cristales para corte AT son los más comunes en la producción en masa de materiales para osciladores; la forma y las dimensiones están optimizadas para un alto rendimiento de las obleas requeridas . Los cristales de cuarzo de alta pureza se cultivan con un contenido especialmente bajo de aluminio, metales alcalinos y otras impurezas y defectos mínimos; la baja cantidad de metales alcalinos proporciona una mayor resistencia a la radiación ionizante. Los cristales para relojes de pulsera, para cortar los cristales de diapasón de 32768 Hz, se cultivan con una densidad de canal de grabado muy baja.
Los cristales para dispositivos SAW se cultivan como planos, con semillas grandes de tamaño X y con baja densidad de canales de grabado.
Los cristales especiales de alto Q, para su uso en osciladores altamente estables, se cultivan a una velocidad lenta constante y tienen una absorción infrarroja baja constante a lo largo de todo el eje Z. Los cristales se pueden cultivar como barra Y, con un cristal semilla en forma de barra y alargado a lo largo del eje Y, o como placa Z, cultivados a partir de una semilla de placa con longitud en la dirección del eje Y y ancho en el eje X. [24] La región alrededor del cristal semilla contiene una gran cantidad de defectos de cristal y no se debe utilizar para las obleas.
Los cristales crecen anisotrópicamente ; el crecimiento a lo largo del eje Z es hasta 3 veces más rápido que a lo largo del eje X. La dirección y la velocidad de crecimiento también influyen en la velocidad de absorción de impurezas. [27] Los cristales de barra Y, o cristales de placa Z con eje Y largo, tienen cuatro regiones de crecimiento generalmente llamadas +X, −X, Z y S. [28] La distribución de impurezas durante el crecimiento es desigual; diferentes áreas de crecimiento contienen diferentes niveles de contaminantes. Las regiones Z son las más puras, las pequeñas regiones S ocasionalmente presentes son menos puras, la región +X es aún menos pura y la región -X tiene el nivel más alto de impurezas. Las impurezas tienen un impacto negativo en la dureza de la radiación , la susceptibilidad al maclado , la pérdida de filtro y la estabilidad a largo y corto plazo de los cristales. [29] Las semillas de diferentes cortes en diferentes orientaciones pueden proporcionar otros tipos de regiones de crecimiento. [30] La velocidad de crecimiento de la dirección −X es más lenta debido al efecto de la adsorción de moléculas de agua en la superficie del cristal; las impurezas de aluminio suprimen el crecimiento en otras dos direcciones. El contenido de aluminio es más bajo en la región Z, más alto en +X, pero más alto en −X y más alto en S; el tamaño de las regiones S también crece con una mayor cantidad de aluminio presente. El contenido de hidrógeno es más bajo en la región Z, más alto en la región +X, pero más alto en la región S y más alto en −X. [31] Las inclusiones de aluminio se transforman en centros de color con la irradiación de rayos gamma, lo que provoca un oscurecimiento del cristal proporcional a la dosis y el nivel de impurezas; la presencia de regiones con diferente oscuridad revela las diferentes regiones de crecimiento.
El tipo dominante de defecto de preocupación en los cristales de cuarzo es la sustitución de un átomo de Al(III) por un átomo de Si(IV) en la red cristalina . El ion de aluminio tiene un compensador de carga intersticial asociado presente cerca, que puede ser un ion H + (unido al oxígeno cercano y formando un grupo hidroxilo , llamado defecto Al−OH), ion Li + , ion Na + , ion K + (menos común), o un hueco de electrón atrapado en un orbital de un átomo de oxígeno cercano. La composición de la solución de crecimiento, ya sea a base de compuestos alcalinos de litio o sodio, determina los iones compensadores de carga para los defectos de aluminio. Las impurezas de iones son preocupantes ya que no están firmemente unidas y pueden migrar a través del cristal, alterando la elasticidad de la red local y la frecuencia de resonancia del cristal. Otras impurezas comunes de preocupación son, por ejemplo, hierro (III) (intersticial), flúor, boro (III), fósforo (V) (sustitución), titanio (IV) (sustitución, universalmente presente en cuarzo magmático, menos común en cuarzo hidrotermal) y germanio (IV) (sustitución). Los iones de sodio y hierro pueden causar inclusiones de cristales de acnita y elemeusita. Las inclusiones de agua pueden estar presentes en cristales de crecimiento rápido; las moléculas de agua intersticiales son abundantes cerca de la semilla del cristal. Otro defecto de importancia es el defecto de crecimiento que contiene hidrógeno, cuando en lugar de una estructura Si-O-Si, se forma un par de grupos Si-OH HO-Si; esencialmente un enlace hidrolizado. Los cristales de crecimiento rápido contienen más defectos de hidrógeno que los de crecimiento lento. Estos defectos de crecimiento son una fuente de suministro de iones de hidrógeno para procesos inducidos por radiación y la formación de defectos de Al-OH. Las impurezas de germanio tienden a atrapar electrones creados durante la irradiación; Los cationes de metales alcalinos migran entonces hacia el centro cargado negativamente y forman un complejo estabilizador. También pueden estar presentes defectos de matriz; vacantes de oxígeno, vacantes de silicio (generalmente compensadas por 4 hidrógenos o 3 hidrógenos y un hueco), grupos peroxi, etc. Algunos de los defectos producen niveles localizados en la banda prohibida, que sirven como trampas de carga; Al(III) y B(III) típicamente sirven como trampas de huecos mientras que las vacantes de electrones, los átomos de titanio, germanio y fósforo sirven como trampas de electrones. Los portadores de carga atrapados pueden liberarse mediante calentamiento; su recombinación es la causa de la termoluminiscencia .
La movilidad de los iones intersticiales depende en gran medida de la temperatura. Los iones de hidrógeno son móviles hasta 10 K, pero los iones de metales alcalinos se vuelven móviles solo a temperaturas cercanas o superiores a 200 K. Los defectos de hidroxilo se pueden medir mediante espectroscopia de infrarrojo cercano. Los agujeros atrapados se pueden medir mediante resonancia de espín electrónico . Los defectos de Al−Na + se muestran como un pico de pérdida acústica debido a su movimiento inducido por la tensión; los defectos de Al−Li + no forman un pozo de potencial, por lo que no son detectables de esta manera. [32] Algunos de los defectos inducidos por radiación durante su recocido térmico producen termoluminiscencia ; se pueden distinguir defectos relacionados con el aluminio, el titanio y el germanio. [33]
Los cristales barridos son cristales que han sido sometidos a un proceso de purificación por electrodifusión en estado sólido . El barrido implica calentar el cristal por encima de 500 °C en una atmósfera libre de hidrógeno, con un gradiente de voltaje de al menos 1 kV/cm, durante varias horas (normalmente más de 12). La migración de impurezas y el reemplazo gradual de iones de metales alcalinos por hidrógeno (cuando se barren en el aire) o huecos de electrones (cuando se barren en el vacío) provoca una corriente eléctrica débil a través del cristal; la descomposición de esta corriente a un valor constante señala el final del proceso. A continuación, se deja enfriar el cristal, mientras se mantiene el campo eléctrico. Las impurezas se concentran en la región del cátodo del cristal, que se corta después y se descarta. [34] Los cristales barridos tienen una mayor resistencia a la radiación, ya que los efectos de la dosis dependen del nivel de impurezas de metales alcalinos; son adecuados para su uso en dispositivos expuestos a la radiación ionizante, por ejemplo, para la tecnología nuclear y espacial. [35] El barrido al vacío a temperaturas más altas y mayores intensidades de campo produce cristales aún más resistentes a la radiación. [36] El nivel y el carácter de las impurezas se pueden medir mediante espectroscopia infrarroja. [37] El cuarzo se puede barrer tanto en fase α como β; el barrido en fase β es más rápido, pero la transición de fase puede inducir maclado. El maclado se puede mitigar sometiendo el cristal a una tensión de compresión en la dirección X, o a un campo eléctrico de CA o CC a lo largo del eje X mientras el cristal se enfría a través de la región de temperatura de transformación de fase. [36]
El barrido también se puede utilizar para introducir un tipo de impureza en el cristal. Los cristales barridos de litio, sodio e hidrógeno se utilizan, por ejemplo, para estudiar el comportamiento del cuarzo.
Se pueden fabricar cristales muy pequeños para frecuencias de modo fundamental altas mediante fotolitografía. [26]
Los cristales se pueden ajustar a frecuencias exactas mediante el recorte por láser . Una técnica utilizada en el mundo de la radioafición para una ligera disminución de la frecuencia del cristal se puede lograr exponiendo cristales con electrodos de plata a vapores de yodo , lo que provoca un ligero aumento de masa en la superficie mediante la formación de una fina capa de yoduro de plata ; sin embargo, estos cristales tenían una estabilidad problemática a largo plazo. Otro método comúnmente utilizado es el aumento o disminución electroquímica del espesor del electrodo de plata sumergiendo un resonador en lapislázuli disuelto en agua, ácido cítrico en agua o agua con sal, y utilizando el resonador como un electrodo y un pequeño electrodo de plata como el otro.
Eligiendo la dirección de la corriente se puede aumentar o disminuir la masa de los electrodos. Los detalles fueron publicados en la revista "Radio" (3/1978) por UB5LEV.
No se recomienda aumentar la frecuencia raspando partes de los electrodos, ya que esto puede dañar el cristal y reducir su factor Q. También se pueden utilizar recortadores de capacitores para ajustar la frecuencia del circuito oscilador.
Se pueden emplear otros materiales piezoeléctricos distintos del cuarzo. Estos incluyen cristales individuales de tantalato de litio , niobato de litio , borato de litio , berlinita , arseniuro de galio , tetraborato de litio , fosfato de aluminio , óxido de bismuto y germanio , cerámicas de titanato de circonio policristalino, cerámicas con alto contenido de alúmina, compuestos de óxido de silicio y zinc o tartrato de dipotasio . [38] [39] Algunos materiales pueden ser más adecuados para aplicaciones específicas. También se puede fabricar un cristal oscilador depositando el material del resonador sobre la superficie del chip de silicio. [40] Los cristales de fosfato de galio , langasita , langanita y langatato son aproximadamente 10 veces más extraíbles que los cristales de cuarzo correspondientes y se utilizan en algunos osciladores VCXO. [41]
La estabilidad de frecuencia está determinada por la Q del cristal . Depende inversamente de la frecuencia y de la constante que depende del corte particular. Otros factores que influyen en la Q son el sobretono utilizado, la temperatura, el nivel de excitación del cristal, la calidad del acabado de la superficie, las tensiones mecánicas impuestas al cristal por la unión y el montaje, la geometría del cristal y los electrodos unidos, la pureza del material y los defectos en el cristal, el tipo y la presión del gas en el recinto, los modos de interferencia y la presencia y dosis absorbida de radiación ionizante y neutrónica.
La estabilidad de los cristales de corte AT disminuye con el aumento de la frecuencia. Para frecuencias más altas y precisas, es mejor utilizar un cristal con una frecuencia fundamental más baja, que funcione en un sobretono.
Un circuito oscilador mal diseñado puede comenzar a oscilar repentinamente en un sobretono . En 1972, un tren en Fremont, California, se estrelló debido a un oscilador defectuoso. Un valor inadecuado del condensador del tanque provocó que el cristal de una placa de control se sobreexigiera, saltando a un sobretono y haciendo que el tren acelerara en lugar de disminuir la velocidad. [42]
La temperatura influye en la frecuencia de funcionamiento; se utilizan varias formas de compensación, desde la compensación analógica (TCXO) y la compensación por microcontrolador (MCXO) hasta la estabilización de la temperatura con un horno de cristal (OCXO). Los cristales poseen histéresis de temperatura ; la frecuencia a una temperatura dada que se logra al aumentar la temperatura no es igual a la frecuencia a la misma temperatura que se logra al disminuir la temperatura. La sensibilidad a la temperatura depende principalmente del corte; los cortes con compensación de temperatura se eligen para minimizar la dependencia de la frecuencia/temperatura. Se pueden realizar cortes especiales con características de temperatura lineal; el corte LC se utiliza en termómetros de cuarzo. Otros factores influyentes son el sobretono utilizado, el montaje y los electrodos, las impurezas en el cristal, la tensión mecánica, la geometría del cristal, la velocidad de cambio de temperatura, el historial térmico (debido a la histéresis), la radiación ionizante y el nivel de excitación.
Los cristales tienden a sufrir anomalías en sus características de frecuencia/temperatura y resistencia/temperatura, conocidas como caídas de actividad. Se trata de pequeñas excursiones descendentes de frecuencia o ascendentes de resistencia localizadas a ciertas temperaturas, cuya posición de temperatura depende del valor de los capacitores de carga.
Las tensiones mecánicas también influyen en la frecuencia. Las tensiones pueden ser inducidas por el montaje, la unión y la aplicación de los electrodos, por la expansión térmica diferencial del montaje, los electrodos y el propio cristal, por tensiones térmicas diferenciales cuando hay un gradiente de temperatura presente, por la expansión o contracción de los materiales de unión durante el curado, por la presión del aire que se transfiere a la presión ambiental dentro del recinto del cristal, por las tensiones de la propia red cristalina (crecimiento no uniforme, impurezas, dislocaciones), por las imperfecciones de la superficie y los daños causados durante la fabricación, y por la acción de la gravedad sobre la masa del cristal; por lo tanto, la frecuencia puede verse influida por la posición del cristal. Otros factores inductores de tensiones dinámicas son los golpes, las vibraciones y el ruido acústico. Algunos cortes son menos sensibles a las tensiones; el corte SC (compensado por tensiones) es un ejemplo. Los cambios de presión atmosférica también pueden introducir deformaciones en la carcasa, lo que influye en la frecuencia al cambiar las capacitancias parásitas.
La humedad atmosférica influye en las propiedades de transferencia térmica del aire y puede cambiar las propiedades eléctricas de los plásticos mediante la difusión de moléculas de agua en su estructura, alterando las constantes dieléctricas y la conductividad eléctrica . [43]
Otros factores que influyen en la frecuencia son la tensión de alimentación, la impedancia de carga, los campos magnéticos, los campos eléctricos (en caso de cortes sensibles a ellos, por ejemplo, cortes SC), la presencia y dosis absorbida de partículas γ y radiación ionizante, y la edad del cristal.
Los cristales sufren un cambio gradual y lento de frecuencia con el tiempo, conocido como envejecimiento. Hay muchos mecanismos involucrados. El montaje y los contactos pueden experimentar un alivio de las tensiones incorporadas. Las moléculas de contaminación, ya sea de la atmósfera residual, desgasificadas del cristal, los electrodos o los materiales de embalaje, o introducidas durante el sellado de la carcasa, pueden adsorberse en la superficie del cristal, cambiando su masa; este efecto se explota en microbalanzas de cristal de cuarzo . La composición del cristal puede alterarse gradualmente por desgasificación, difusión de átomos de impurezas o migración desde los electrodos, o la red puede dañarse por radiación. Pueden ocurrir reacciones químicas lentas sobre o dentro del cristal, o en las superficies internas de la carcasa. El material del electrodo, por ejemplo, cromo o aluminio, puede reaccionar con el cristal, creando capas de óxido de metal y silicio; estas capas de interfaz pueden sufrir cambios con el tiempo. La presión en la carcasa puede cambiar debido a la variación de la presión atmosférica, la temperatura, las fugas o la desgasificación de los materiales del interior. Los factores externos al propio cristal son, por ejemplo, el envejecimiento de los circuitos del oscilador (y, por ejemplo, el cambio de capacitancias) y la deriva de los parámetros del horno de cristal. La composición de la atmósfera externa también puede influir en el envejecimiento; el hidrógeno puede difundirse a través de la carcasa de níquel. El helio puede causar problemas similares cuando se difunde a través de los recintos de vidrio de los estándares de rubidio . [44]
El oro es un material de electrodo preferido para resonadores de bajo envejecimiento; su adhesión al cuarzo es lo suficientemente fuerte como para mantener el contacto incluso con fuertes choques mecánicos, pero lo suficientemente débil como para no soportar gradientes de tensión significativos (a diferencia del cromo, aluminio y níquel). El oro tampoco forma óxidos; adsorbe contaminantes orgánicos del aire, pero estos son fáciles de eliminar. Sin embargo, el oro solo puede sufrir delaminación; por lo tanto, a veces se usa una capa de cromo para mejorar la fuerza de unión. La plata y el aluminio se utilizan a menudo como electrodos; sin embargo, ambos forman capas de óxido con el tiempo que aumentan la masa del cristal y reducen la frecuencia. La plata se puede pasivar mediante la exposición a vapores de yodo , formando una capa de yoduro de plata . El aluminio se oxida fácilmente pero lentamente, hasta que se alcanza un espesor de aproximadamente 5 nm; el aumento de temperatura durante el envejecimiento artificial no aumenta significativamente la velocidad de formación de óxido; se puede formar una capa gruesa de óxido durante la fabricación mediante anodizado . [45] La exposición del cristal plateado a vapores de yodo también se puede utilizar en condiciones de aficionado para reducir ligeramente la frecuencia del cristal; La frecuencia también se puede aumentar raspando partes de los electrodos, pero eso conlleva el riesgo de dañar el cristal y perder Q.
Una polarización de voltaje de CC entre los electrodos puede acelerar el envejecimiento inicial, probablemente por difusión inducida de impurezas a través del cristal. Colocar un capacitor en serie con el cristal y una resistencia de varios megaohmios en paralelo puede minimizar dichos voltajes.
El envejecimiento disminuye de forma logarítmica con el tiempo y los cambios más importantes se producen poco después de la fabricación. El envejecimiento artificial de un cristal mediante un almacenamiento prolongado a una temperatura de entre 85 y 125 °C puede aumentar su estabilidad a largo plazo.
Los cristales son sensibles a los golpes . La tensión mecánica provoca un cambio a corto plazo en la frecuencia del oscilador debido a la sensibilidad al estrés del cristal, y puede introducir un cambio permanente de frecuencia debido a cambios inducidos por el choque en el montaje y tensiones internas (si se exceden los límites elásticos de las partes mecánicas), desorción de contaminación de las superficies del cristal o cambio en los parámetros del circuito del oscilador. Los golpes de gran magnitud pueden arrancar los cristales de sus montajes (especialmente en el caso de grandes cristales de baja frecuencia suspendidos en cables delgados) o provocar el agrietamiento del cristal. Los cristales libres de imperfecciones en la superficie son altamente resistentes a los golpes; el pulido químico puede producir cristales capaces de sobrevivir a decenas de miles de g . [46]
Los cristales no tienen mecanismos de falla inherentes; algunos han estado funcionando en dispositivos durante décadas. Sin embargo, las fallas pueden ser introducidas por fallas en la unión, carcasas con fugas, corrosión, cambio de frecuencia por envejecimiento, rotura del cristal por un choque mecánico demasiado fuerte o daño inducido por radiación cuando se utiliza cuarzo sin barrido . [47] Los cristales también pueden resultar dañados por una sobreexcitación.
Los cristales también sufren pequeñas fluctuaciones de frecuencia a corto plazo. Las principales causas de dicho ruido son, por ejemplo, el ruido térmico (que limita el nivel de ruido), la dispersión de fonones (influenciada por defectos de la red), la adsorción/desorción de moléculas en la superficie del cristal, el ruido de los circuitos del oscilador, los choques y vibraciones mecánicas, los cambios de aceleración y orientación, las fluctuaciones de temperatura y el alivio de las tensiones mecánicas. La estabilidad a corto plazo se mide mediante cuatro parámetros principales: la varianza de Allan (la más común especificada en las hojas de datos de los osciladores), el ruido de fase, la densidad espectral de las desviaciones de fase y la densidad espectral de las desviaciones de frecuencia fraccionarias. Los efectos de la aceleración y la vibración tienden a dominar las otras fuentes de ruido; los dispositivos de ondas acústicas de superficie tienden a ser más sensibles que los de ondas acústicas en masa (BAW), y los cortes compensados por tensión son incluso menos sensibles. La orientación relativa del vector de aceleración con respecto al cristal influye drásticamente en la sensibilidad a la vibración del cristal. Se pueden utilizar soportes de aislamiento de vibraciones mecánicas para cristales de alta estabilidad.
El ruido de fase desempeña un papel importante en los sistemas de síntesis de frecuencia que utilizan la multiplicación de frecuencia; una multiplicación de una frecuencia por N aumenta la potencia del ruido de fase en N 2 . Una multiplicación de frecuencia por 10 veces multiplica la magnitud del error de fase por 10 veces. Esto puede ser desastroso para los sistemas que emplean tecnologías PLL o FSK .
Los campos magnéticos tienen poco efecto sobre el cristal en sí, ya que el cuarzo es diamagnético ; sin embargo, se pueden inducir corrientes de Foucault o voltajes de CA en los circuitos y las partes magnéticas del montaje y la carcasa pueden verse afectadas.
Después de encenderlos, los cristales tardan varios segundos o minutos en "calentarse" y estabilizar su frecuencia. Los osciladores OCXO controlados por horno suelen necesitar entre 3 y 10 minutos para calentarse y alcanzar el equilibrio térmico; los osciladores sin horno se estabilizan en varios segundos, ya que los pocos milivatios disipados en el cristal provocan un nivel pequeño pero perceptible de calentamiento interno. [48]
Los cristales deben ser accionados al nivel de accionamiento apropiado. Los cristales de baja frecuencia, especialmente los de modo flexural, pueden fracturarse a niveles de accionamiento demasiado altos. El nivel de accionamiento se especifica como la cantidad de potencia disipada en el cristal. Los niveles de accionamiento apropiados son aproximadamente 5 μW para modos flexurales de hasta 100 kHz, 1 μW para modos fundamentales de 1 a 4 MHz, 0,5 μW para modos fundamentales de 4 a 20 MHz y 0,5 μW para modos de sobretono de 20 a 200 MHz. [49] Un nivel de accionamiento demasiado bajo puede causar problemas con el arranque del oscilador. Los niveles de accionamiento bajos son mejores para una mayor estabilidad y un menor consumo de energía del oscilador. Los niveles de accionamiento más altos, a su vez, reducen el impacto del ruido al aumentar la relación señal-ruido . [50]
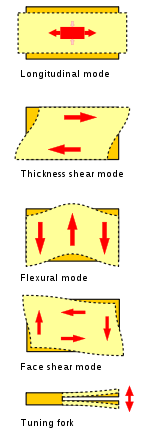
La placa resonadora se puede cortar del cristal fuente de muchas maneras diferentes. La orientación del corte influye en las características de envejecimiento del cristal, la estabilidad de frecuencia, las características térmicas y otros parámetros. Estos cortes funcionan con ondas acústicas en masa (BAW); para frecuencias más altas, se emplean dispositivos de ondas acústicas de superficie (SAW).
Imagen de varios cortes de cristal [51]
La letra "T" en el nombre del corte marca un corte con compensación de temperatura, un corte orientado de manera tal que los coeficientes de temperatura de la red son mínimos; los cortes FC y SC también están compensados por temperatura.
Los cortes de alta frecuencia se montan por sus bordes, generalmente sobre resortes; la rigidez del resorte debe ser óptima, ya que si es demasiado rígido, los choques mecánicos podrían transferirse al cristal y hacer que se rompa, y una rigidez demasiado baja puede hacer que el cristal colisione con el interior del encapsulado cuando se somete a un choque mecánico y se rompa. Los resonadores de tira, generalmente cortes AT, son más pequeños y, por lo tanto, menos sensibles a los choques mecánicos. A la misma frecuencia y armónico, la tira tiene menos capacidad de tracción, mayor resistencia y mayor coeficiente de temperatura. [69]
Los cortes de baja frecuencia se montan en los nodos donde están prácticamente inmóviles; en esos puntos, a cada lado, se fijan cables delgados entre el cristal y los conductores. La gran masa del cristal suspendido en los cables delgados hace que el conjunto sea sensible a los choques mecánicos y las vibraciones. [52]
Los cristales suelen estar montados en cajas de vidrio o metal herméticamente selladas, llenas de una atmósfera seca e inerte, generalmente de vacío, nitrógeno o helio. También se pueden utilizar cajas de plástico, pero no son herméticas y se debe construir otro sellado secundario alrededor del cristal.
Son posibles varias configuraciones de resonador, además de la forma clásica de unir directamente los cables al cristal. Por ejemplo, el resonador BVA (Boîtier à Vieillissement Amélioré, Enclosure with Improved Aging), [70] [ ¿fuente no confiable? ] desarrollado en 1976; las partes que influyen en las vibraciones están mecanizadas a partir de un solo cristal (lo que reduce la tensión de montaje), y los electrodos no se depositan en el propio resonador sino en los lados internos de dos discos condensadores hechos de rodajas adyacentes del cuarzo de la misma barra, formando un sándwich de tres capas sin tensión entre los electrodos y el elemento vibrante. El espacio entre los electrodos y el resonador actúa como dos pequeños condensadores en serie, lo que hace que el cristal sea menos sensible a las influencias del circuito. [71] [ ¿fuente no confiable? ] La arquitectura elimina los efectos de los contactos superficiales entre los electrodos, las limitaciones en las conexiones de montaje y los problemas relacionados con la migración de iones desde los electrodos hacia la red del elemento vibrante. [72] La configuración resultante es robusta, resistente a golpes y vibraciones, resistente a la aceleración y la radiación ionizante, y tiene características de envejecimiento mejoradas. Generalmente se utiliza el corte AT, aunque también existen variantes de corte SC. Los resonadores BVA se utilizan a menudo en aplicaciones de naves espaciales. [73]
Entre los años 1930 y 1950, era bastante común que la gente ajustara la frecuencia de los cristales mediante un pulido manual. Los cristales se molían utilizando una suspensión abrasiva fina, o incluso una pasta de dientes, para aumentar su frecuencia. Se podía lograr una ligera disminución de 1 a 2 kHz cuando el cristal se molía en exceso marcando la cara del cristal con una mina de lápiz, a costa de una Q reducida . [74]
La frecuencia del cristal es ligeramente ajustable ("pullable") modificando las capacitancias adjuntas. Un varactor , un diodo con capacitancia que depende del voltaje aplicado, se utiliza a menudo en osciladores de cristal controlados por voltaje, VCXO. Los cortes de cristal son normalmente AT o raramente SC, y funcionan en modo fundamental; la cantidad de desviación de frecuencia disponible es inversamente proporcional al cuadrado del número de sobretono, por lo que un tercer sobretono tiene solo una novena parte de la pullabilidad del modo fundamental. Los cortes SC, aunque más estables, son significativamente menos pullables. [75]
En los diagramas esquemáticos eléctricos, los cristales se designan con la letra de clase Y (Y1, Y2, etc.). Los osciladores, ya sean de cristal u otros, se designan con la letra de clase G (G1, G2, etc.). [76] [77] Los cristales también pueden designarse en un esquema con X o XTAL (una abreviatura fonética, comparable a usar Xmas para Navidad ), o un oscilador de cristal con XO .
Tipos de osciladores de cristal y sus abreviaturas: