Base de Gröbner

Constructo matemático en álgebra computacional

En matemáticas , y más específicamente en álgebra computacional , geometría algebraica computacional y álgebra conmutativa computacional , una base de Gröbner es un tipo particular de conjunto generador de un ideal en un anillo polinomial K [ x ₁ , ..., x _n ] sobre un cuerpo K. Una base de Gröbner permite deducir fácilmente muchas propiedades importantes del ideal y la variedad algebraica asociada, como la dimensión y el número de ceros cuando es finito. El cálculo de la base de Gröbner es una de las principales herramientas prácticas para resolver sistemas de ecuaciones polinómicas y calcular las imágenes de variedades algebraicas bajo proyecciones o mapas racionales .

El cálculo de la base de Gröbner puede verse como una generalización multivariada y no lineal tanto del algoritmo de Euclides para calcular los máximos comunes divisores de polinomios como de la eliminación gaussiana para sistemas lineales. ^[1]

Las bases de Gröbner fueron introducidas por Bruno Buchberger en su tesis doctoral de 1965, que también incluía un algoritmo para calcularlas ( el algoritmo de Buchberger ). Las nombró en honor a su asesor Wolfgang Gröbner . En 2007, Buchberger recibió el Premio Paris Kanellakis de Teoría y Práctica de la Asociación de Maquinaria Computacional por este trabajo. Sin embargo, el matemático ruso Nikolai Günther había introducido una noción similar en 1913, publicada en varias revistas matemáticas rusas. Estos artículos fueron en gran medida ignorados por la comunidad matemática hasta su redescubrimiento en 1987 por Bodo Renschuch et al. ^[2] Un concepto análogo para las series de potencias multivariadas fue desarrollado independientemente por Heisuke Hironaka en 1964, quien las nombró bases estándar . Este término ha sido utilizado por algunos autores para denotar también las bases de Gröbner.

La teoría de las bases de Gröbner ha sido extendida por muchos autores en diversas direcciones. Se ha generalizado a otras estructuras como polinomios sobre anillos de ideales principales o anillos polinómicos , y también a algunas clases de anillos no conmutativos y álgebras, como las álgebras de Ore .

Herramientas

Anillo polinomial

Las bases de Gröbner se definen principalmente para ideales en un anillo de polinomios sobre un cuerpo K. Aunque la teoría funciona para cualquier cuerpo, la mayoría de los cálculos de la base de Gröbner se realizan cuando K es el cuerpo de los racionales o de los enteros módulo un número primo. ${\displaystyle R=K[x_{1},\ldots ,x_{n}]}$

En el contexto de las bases de Gröbner, un polinomio distinto de cero en se representa comúnmente como una suma donde los son elementos distintos de cero de K , llamados coeficientes , y los son monomios (llamados productos de potencia por Buchberger y algunos de sus seguidores) de la forma donde los son números enteros no negativos. El vector se llama vector exponente del monomio. Cuando la lista de las variables es fija, la notación de los monomios a menudo se abrevia como ${\displaystyle R=K[x_{1},\ldots ,x_{n}]}$ ${\displaystyle c_{1}M_{1}+\cdots +c_{m}M_{m},}$ ${\displaystyle c_{i}}$ ${\displaystyle M_{i}}$ ${\displaystyle x_{1}^{a_{1}}\cdots x_{n}^{a_{n}},}$ ${\displaystyle a_{i}}$ ${\displaystyle A=[a_{1},\ldots ,a_{n}]}$ ${\displaystyle X=[x_{1},\ldots ,x_{n}]}$ ${\displaystyle x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}=X^{A}.}$

Los monomios se definen de forma única por sus vectores exponentes y, cuando se fija un orden de monomios (ver más abajo), un polinomio se representa de forma única por la lista ordenada de pares ordenados formados por un vector exponente y el coeficiente correspondiente. Esta representación de polinomios es especialmente eficiente para el cálculo de la base de Gröbner en computadoras, aunque es menos conveniente para otros cálculos como la factorización de polinomios y el máximo común divisor de polinomios .

Si es un conjunto finito de polinomios en el anillo de polinomios R , el ideal generado por F es el conjunto de combinaciones lineales de elementos de F con coeficientes en R ; es decir, el conjunto de polinomios que se pueden escribir con ${\displaystyle F=\{f_{1},\ldots ,f_{k}\}}$ ${\textstyle \sum _{i=1}^{k}g_{i}f_{i}}$ ${\displaystyle g_{1},\ldots ,g_{k}\in R.}$

Ordenamiento monomial

Todas las operaciones relacionadas con las bases de Gröbner requieren la elección de un orden total en los monomios, con las siguientes propiedades de compatibilidad con la multiplicación. Para todos los monomios M , N , P ,

1. ${\displaystyle M\leq N\Longleftrightarrow MP\leq NP}$
2. ${\displaystyle M\leq MP}$.

Un orden total que satisface estas condiciones a veces se denomina orden admisible .

Estas condiciones implican que el orden es un buen orden , es decir, toda secuencia estrictamente decreciente de monomios es finita.

Aunque la teoría de la base de Gröbner no depende de una elección particular de un ordenamiento monomial admisible, tres ordenamientos monomiales son especialmente importantes para las aplicaciones:

• Ordenamiento lexicográfico , comúnmente llamado lex o plex (para ordenamiento léxico puro).
• Orden lexicográfico inverso de grado total , comúnmente llamado degrevlex .
• Orden de eliminación , lexdeg .

La teoría de la base de Gröbner se introdujo inicialmente para la ordenación lexicográfica. Pronto se comprendió que la base de Gröbner para degrevlex es casi siempre mucho más fácil de calcular, y que casi siempre es más fácil calcular una base de Gröbner de lex calculando primero la base degrevlex y luego utilizando un "algoritmo de cambio de ordenación". Cuando se necesita eliminación, degrevlex no es conveniente; se pueden utilizar tanto lex como lexdeg pero, nuevamente, muchos cálculos son relativamente fáciles con lexdeg y casi imposibles con lex.

Operaciones básicas

Término principal, coeficiente y monomio

Una vez que se fija el orden de un monomio, los términos de un polinomio (producto de un monomio por su coeficiente distinto de cero) se ordenan naturalmente por monomios decrecientes (para este orden). Esto hace que la representación de un polinomio como una lista ordenada de pares de vectores coeficiente-exponente sea una representación canónica de los polinomios (es decir, dos polinomios son iguales si y solo si tienen la misma representación).

El primer término (mayor) de un polinomio p para este ordenamiento y el monomio y coeficiente correspondientes se denominan respectivamente término principal , monomio principal y coeficiente principal y se denotan, en este artículo, lt( p ), lm( p ) y lc( p ) .

La mayoría de las operaciones polinómicas relacionadas con las bases de Gröbner involucran los términos principales. Por lo tanto, la representación de polinomios como listas ordenadas hace que estas operaciones sean particularmente eficientes (leer el primer elemento de una lista requiere un tiempo constante, independientemente de la longitud de la lista).

Operaciones polinómicas

Las demás operaciones polinómicas implicadas en los cálculos de la base de Gröbner también son compatibles con el ordenamiento monomial; es decir, se pueden realizar sin reordenar el resultado:

• La suma de dos polinomios consiste en una fusión de las dos listas de términos correspondientes, con un tratamiento especial en caso de conflicto (es decir, cuando el mismo monomio aparece en los dos polinomios).
• La multiplicación de un polinomio por un escalar consiste en multiplicar cada coeficiente por este escalar, sin ningún otro cambio en la representación.
• La multiplicación de un polinomio por un monomio m consiste en multiplicar cada monomio del polinomio por m . Esto no cambia el término ordenación por definición de ordenación de un monomio.

Divisibilidad de monomios

Sean y dos monomios, con vectores exponentes y ${\displaystyle M=x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}}$ ${\displaystyle N=x_{1}^{b_{1}}\cdots x_{n}^{b_{n}}}$ ${\displaystyle A=[a_{1},\ldots ,a_{n}]}$ ${\displaystyle B=[b_{1},\ldots ,b_{n}].}$

Se dice que M divide a N , o que N es múltiplo de M , si para todo i ; es decir, si A no es mayor que B por componentes . En este caso, el cociente se define como En otras palabras, el vector exponente de es la resta por componentes de los vectores exponentes de N y M . ${\displaystyle a_{i}\leq b_{i}}$ ${\textstyle {\frac {N}{M}}}$ ${\textstyle {\frac {N}{M}}=x_{1}^{b_{1}-a_{1}}\cdots x_{n}^{b_{n}-a_{n}}.}$ ${\textstyle {\frac {N}{M}}}$

El máximo común divisor mcd( M , N ) de M y N es el monomio cuyo vector exponente es el mínimo componente de A y B . El mínimo común múltiplo mcm( M , N ) se define de manera similar con max en lugar de min . ${\textstyle x_{1}^{\min(a_{1},b_{1})}\cdots x_{n}^{\min(a_{n},b_{n})}}$

Uno tiene

${\displaystyle \operatorname {lcm} (M,N)={\frac {MN}{\gcd(M,N)}}.}$

Reducción

La reducción de un polinomio por otros polinomios con respecto a un orden monomial es central para la teoría de la base de Gröbner. Es una generalización tanto de la reducción por filas que ocurre en los pasos de eliminación gaussiana como de división de la división euclidiana de polinomios univariados . ^[1] Cuando se completa tanto como sea posible, a veces se denomina división multivariada , aunque su resultado no está definido de forma única.

La reducción de adelanto es un caso especial de reducción que es más fácil de calcular. Es fundamental para el cálculo de la base de Gröbner, ya que la reducción general solo se necesita al final de un cálculo de la base de Gröbner, para obtener una base de Gröbner reducida a partir de una no reducida.

Sea fijado un ordenamiento monomial admisible, al cual se refiere cada comparación monomial que ocurrirá en esta sección.

Un polinomio f es reducible por otro polinomio g si el monomio principal lm( f ) es un múltiplo de lm( g ) . El polinomio f es reducible por g si algún monomio de f es un múltiplo de lm( g ) . (Por lo tanto, si f es reducible por g , también es reducible, pero f puede ser reducible sin ser reducible por el primer polinomio).

Supóngase que f es reducible por g , y sea cm un término de f tal que el monomio m es un múltiplo de lm( g ) . Una reducción de un paso de f por g consiste en reemplazar f por

${\displaystyle \operatorname {red} _{1}(f,g)=f-{\frac {c}{\operatorname {lc} (g)}}\,{\frac {m}{\operatorname {lm} (g)}}\,g.}$

Esta operación elimina el monomio m de f sin cambiar los términos con un monomio mayor que m (para el ordenamiento de monomios). En particular, una reducción de f en un paso produce un polinomio cuyos monomios son todos menores que lm( f ) .

Dado un conjunto finito G de polinomios, se dice que f es reducible o reducible por G si es reducible o reducible por, respectivamente, al menos por un elemento g de G. En este caso, una reducción de un paso (resp. reducción por adelanto de un paso) de f por G es cualquier reducción de un paso (resp. reducción por adelanto de un paso) de f por un elemento de G.

La reducción (completa) (o reducción de adelanto) de f por G consiste en iterar reducciones de un paso (o reducciones de adelanto de un paso) hasta obtener un polinomio que es irreducible (o irreducible de adelanto) por G . A veces se le llama forma normal de f por G . En general, esta forma no está definida de forma unívoca porque, en general, hay varios elementos de G que se pueden usar para reducir f ; esta no unicidad es el punto de partida de la teoría de la base de Gröbner.

La definición de la reducción muestra inmediatamente que, si h es una forma normal de f por G , se tiene

${\displaystyle f=h+\sum _{g\in G}q_{g}\,g,}$

donde h es irreducible por G y son polinomios tales que En el caso de polinomios univariados, si G consta de un único elemento g , entonces h es el resto de la división euclidiana de f por g , y q _g es el cociente. Además, el algoritmo de división es exactamente el proceso de reducción de la derivación. Por esta razón, algunos autores utilizan el término división multivariante en lugar de reducción. ${\displaystyle q_{g}}$ ${\displaystyle \operatorname {lm} (q_{g}\,g)\leq \operatorname {lm} (f).}$

No unicidad de la reducción

En el ejemplo que sigue, hay exactamente dos reducciones de plomo completas que producen dos resultados muy diferentes. El hecho de que los resultados sean irreducibles (no solo irreducibles en plomo) es específico del ejemplo, aunque esto es bastante común en ejemplos tan pequeños.

En este ejemplo de dos variables, el orden monomial que se utiliza es el orden lexicográfico con y consideramos la reducción de , por con ${\displaystyle x>y,}$ ${\displaystyle f=2x^{3}-x^{2}y+y^{3}+3y}$ ${\displaystyle G=\{g_{1},g_{2}\},}$ $${\displaystyle {\begin{aligned}g_{1}&=x^{2}+y^{2}-1,\\g_{2}&=xy-2.\end{aligned}}}$$

Para el primer paso de reducción, se puede reducir tanto el primer término como el segundo de f . Sin embargo, la reducción de un término equivale a eliminar este término a costa de agregar nuevos términos inferiores; si no es el primer término reducible el que se reduce, puede ocurrir que una reducción posterior agregue un término similar, que debe reducirse nuevamente. Por lo tanto, siempre es mejor reducir primero el término reducible más grande (para el orden monomial); es decir, en particular, reducir primero por adelanto hasta obtener un polinomio irreducible por adelanto.

El término principal de f es reducible por y no por Entonces el primer paso de reducción consiste en multiplicar por –2 x y sumar el resultado a f : ${\displaystyle 2x^{3}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{2}.}$ ${\displaystyle g_{1}}$

${\displaystyle f\;\xrightarrow {-2xg_{1}} \;f_{1}=f-2xg_{1}=-x^{2}y-2xy^{2}+2x+y^{3}+3y.}$

El término principal de es un múltiplo de los monomios principales de ambos y Por lo tanto, uno tiene dos opciones para el segundo paso de reducción. Si uno elige, obtiene un polinomio que puede reducirse nuevamente mediante ${\displaystyle -x^{2}y}$ ${\displaystyle f_{1}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{2},}$ ${\displaystyle g_{2},}$ ${\displaystyle g_{2}\colon }$

${\displaystyle f\;\xrightarrow {-2xg_{1}} \;f_{1}\;\xrightarrow {xg_{2}} \;-2xy^{2}+y^{3}+3y\;\xrightarrow {2yg_{2}} \;f_{2}=y^{3}-y.}$

No es posible ninguna reducción adicional, por lo que se trata de una reducción completa de f . ${\displaystyle f_{2}}$

Con la otra opción para el segundo paso se obtiene un resultado diferente:

${\displaystyle f\;\xrightarrow {-2xg_{1}} \;f_{1}\;\xrightarrow {yg_{1}} \;-2xy^{2}+2x+2y^{3}+2y\;\xrightarrow {2yg_{2}} \;f_{3}=2x+2y^{3}-2y.}$

Nuevamente el resultado es irreducible, aunque sólo se realizaron reducciones de plomo. ${\displaystyle f_{3}}$

En resumen, la reducción completa de f puede dar como resultado uno o más de los siguientes: ${\displaystyle f_{2}=y^{3}-y}$ ${\displaystyle f_{3}=2x+2y^{3}-2y.}$

Para resolver los problemas planteados por esta no unicidad, Buchberger introdujo las bases de Gröbner y los polinomios S. Intuitivamente, 0 = f − f puede reducirse a Esto implica que pertenece al ideal generado por G . Por lo tanto, este ideal no se modifica al añadir G , y esto permite más reducciones. En particular, puede reducirse a por y esto restaura la unicidad de la forma reducida. ${\displaystyle f_{2}-f_{3}.}$ ${\displaystyle f_{2}-f_{3}}$ ${\displaystyle f_{3}-f_{2}}$ ${\displaystyle f_{3}}$ ${\displaystyle f_{2}}$ ${\displaystyle f_{3}-f_{2}}$

Aquí el algoritmo de Buchberger para las bases de Gröbner comenzaría añadiendo a G el polinomio

${\displaystyle g_{3}=yg_{1}-xg_{2}=2x+y^{3}-y.}$

Este polinomio, llamado S -polinomio por Buchberger, es la diferencia de las reducciones de un paso del mínimo común múltiplo de los monomios principales de y , por y respectivamente: ${\displaystyle x^{2}y}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{2}}$ ${\displaystyle g_{2}}$ ${\displaystyle g_{1}}$

${\displaystyle g_{3}=\left(x^{2}y-{\frac {x^{2}y}{lt(g_{2})}}g_{2}\right)-\left(x^{2}y-{\frac {x^{2}y}{lt(g_{1})}}g_{1}\right)={\frac {x^{2}y}{lt(g_{1})}}g_{1}-{\frac {x^{2}y}{lt(g_{2})}}g_{2}}$.

En este ejemplo, se tiene Esto no completa el algoritmo de Buchberger, ya que xy da resultados diferentes, cuando se reduce por o ${\displaystyle g_{3}=f_{3}-f_{2}.}$ ${\displaystyle g_{2}}$ ${\displaystyle g_{3}.}$

S-polinomio

Dado el orden monomial, el S-polinomio o par crítico de dos polinomios f y g es el polinomio

${\displaystyle S(f,g)=\operatorname {red} _{1}(\mathrm {lcm} ,g)-\operatorname {red} _{1}(\mathrm {lcm} ,f)}$;

donde mcm denota el mínimo común múltiplo de los monomios principales de f y g . Usando la definición de , esto se traduce a: ${\displaystyle \operatorname {red} _{1}}$

${\displaystyle {\begin{aligned}S(f,g)&=\left(\mathrm {lcm} -{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (g)}}\,g\right)-\left(\mathrm {lcm} -{\frac {1}{\operatorname {lc} (f)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (f)}}\,f\right)\\&={\frac {1}{\operatorname {lc} (f)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (f)}}\,f-{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (g)}}\,g\\\end{aligned}}.}$

Utilizando la propiedad que relaciona el mcm y el mcd , el S -polinomio también se puede escribir como:

${\displaystyle S(f,g)={\frac {1}{\operatorname {lc} (f)}}\,{\frac {\operatorname {lm} (g)}{\mathrm {gcd} }}\,f-{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\operatorname {lm} (f)}{\mathrm {gcd} }}\,g;}$

donde mcd denota el máximo común divisor de los monomios principales de f y g .

Como los monomios que son reducibles tanto por f como por g son exactamente múltiplos de mcm , se pueden tratar todos los casos de no unicidad de la reducción considerando solo los S -polinomios. Este es un hecho fundamental para la teoría de bases de Gröbner y todos los algoritmos para calcularlas.

Para evitar fracciones cuando se trabaja con polinomios con coeficientes enteros, el polinomio S se define a menudo como

${\displaystyle S(f,g)=\operatorname {lc} (g)\,{\frac {\operatorname {lm} (g)}{\mathrm {gcd} }}\,f-\operatorname {lc} (f)\,{\frac {\operatorname {lm} (f)}{\mathrm {gcd} }}\,g;}$

Esto no cambia nada en la teoría ya que los dos polinomios son asociados .

Definición

Sea un anillo polinomial sobre un cuerpo F. En esta sección, suponemos que se ha fijado un ordenamiento monomial admisible. ${\displaystyle R=F[x_{1},\ldots ,x_{n}]}$

Sea G un conjunto finito de polinomios en R que genera un ideal I. El conjunto G es una base de Gröbner (con respecto al ordenamiento monomial), o, más precisamente, una base de Gröbner de I si

1. el ideal generado por los monomios principales de los polinomios en I es igual al ideal generado por los monomios principales de G ,

o, equivalentemente,

2. el monomio principal de cada polinomio en I es un múltiplo del monomio principal de algún polinomio en G.

Existen muchas propiedades caracterizantes, cada una de las cuales puede tomarse como una definición equivalente de las bases de Gröbner. Para ser más concisos, en la siguiente lista, la notación "una palabra/otra palabra" significa que se puede tomar "una palabra" u "otra palabra" para tener dos caracterizaciones diferentes de las bases de Gröbner. Todas las afirmaciones siguientes son caracterizaciones de las bases de Gröbner:

3. un polinomio f está en I , si y sólo si alguna/toda reducción-iniciativa completa de f por G produce el polinomio cero;
4. para cada S -polinomio s de elementos de G , alguna/toda reducción-iniciativa completa/reducción de s por G produce cero;
5. todas las reducciones completas de un elemento de R producen el mismo resultado;
6. Los monomios que son irreducibles por G forman una base del espacio vectorial F ${\displaystyle R/I.}$

Contando la definición anterior, esto proporciona 12 caracterizaciones de bases de Gröbner. El hecho de que sean posibles tantas caracterizaciones hace que las bases de Gröbner sean muy útiles. Por ejemplo, la condición 3 proporciona un algoritmo para probar la pertenencia ideal ; la condición 4 proporciona un algoritmo para probar si un conjunto de polinomios es una base de Gröbner y forma la base del algoritmo de Buchberger para calcular bases de Gröbner; las condiciones 5 y 6 permiten el cálculo de una manera que es muy similar a la aritmética modular . ${\displaystyle R/I}$

Existencia

Para cada ordenación monomial admisible y cada conjunto finito G de polinomios, existe una base de Gröbner que contiene a G y genera el mismo ideal. Además, dicha base de Gröbner puede calcularse con el algoritmo de Buchberger .

Este algoritmo utiliza la condición 4 y procede aproximadamente de la siguiente manera: para dos elementos cualesquiera de G , calcular la reducción completa por G de su S -polinomio y añadir el resultado a G si no es cero; repetir esta operación con los nuevos elementos de G incluidos hasta que, finalmente, todas las reducciones produzcan cero.

El algoritmo siempre termina debido al lema de Dickson o porque los anillos polinómicos son noetherianos ( teorema de la base de Hilbert ). La condición 4 asegura que el resultado sea una base de Gröbner, y las definiciones de S -polinomios y reducción aseguran que el ideal generado no se modifique.

El método anterior es un algoritmo para calcular bases de Gröbner; sin embargo, es muy ineficiente. Se han propuesto e implementado muchas mejoras del algoritmo original de Buchberger y de varios otros algoritmos, que mejoran drásticamente la eficiencia. Véase § Algoritmos e implementaciones, más adelante.

Bases de Gröbner reducidas

Una base de Gröbner esmínima si todos los monomios principales de sus elementos son irreducibles por los otros elementos de la base. Dada una base de Gröbner de un idealI, se obtiene una base de Gröbner mínima deIeliminando los polinomios cuyos monomios principales son múltiplos del monomio principal de otro elemento de la base de Gröbner. Sin embargo, si dos polinomios de la base tienen el mismo monomio principal, solo se debe eliminar uno. Por lo tanto, cada base de Gröbner contiene una base de Gröbner mínima como subconjunto.

Todas las bases de Gröbner mínimas de un ideal dado (para un ordenamiento monomial fijo) tienen el mismo número de elementos y los mismos monomios principales, y las bases de Gröbner no mínimas tienen más elementos que las mínimas.

Una base de Gröbner esreducida si cada polinomio que la compone es irreducible por los demás elementos de la base y tiene1.Por lo tanto, toda base de Gröbner reducida es mínima, pero una base de Gröbner mínima no necesita ser reducida.

Dada una base de Gröbner de un ideal I , se obtiene una base de Gröbner reducida de I eliminando primero los polinomios que son reducibles por los otros elementos de la base (para obtener una base mínima); luego reemplazando cada elemento de la base por el resultado de la reducción completa por los otros elementos de la base; y, finalmente, dividiendo cada elemento de la base por su coeficiente principal.

Todas las bases de Gröbner reducidas de un ideal (para un ordenamiento monomial fijo) son iguales. De ello se deduce que dos ideales son iguales si y solo si tienen la misma base de Gröbner reducida.

A veces, las bases de Gröbner reducidas se definen sin la condición de los coeficientes principales. En este caso, la unicidad de las bases de Gröbner reducidas es cierta solo hasta la multiplicación de polinomios por una constante distinta de cero.

Cuando se trabaja con polinomios en el campo de los números racionales , resulta útil trabajar únicamente con polinomios con coeficientes enteros. En este caso, la condición sobre los coeficientes principales en la definición de una base reducida puede sustituirse por la condición de que todos los elementos de la base sean polinomios primitivos con coeficientes enteros, con coeficientes principales positivos. Esto restablece la unicidad de las bases reducidas. ${\displaystyle \mathbb {Q} }$

Casos especiales

Para cada ordenamiento monomial, el conjunto vacío de polinomios es la única base de Gröbner del ideal cero .

Para cada ordenación monomial, un conjunto de polinomios que contiene una constante distinta de cero es una base de Gröbner del ideal unitario (todo el anillo polinomial). A la inversa, toda base de Gröbner del ideal unitario contiene una constante distinta de cero. La base de Gröbner reducida de la unidad está formada por el único polinomio 1 .

En el caso de polinomios de una sola variable, existe una única ordenación monomial admisible, la ordenación por grado. Las bases de Gröbner mínimas son los singletons constituidos por un único polinomio. Las bases de Gröbner reducidas son los polinomios mónicos .

Ejemplo y contraejemplo

Los ceros de forman la parábola roja; los ceros de forman las tres líneas verticales azules. Su intersección consta de tres puntos. ${\displaystyle f}$ ${\displaystyle g}$

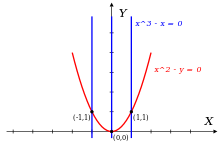
Sea el anillo de polinomios bivariados con coeficientes racionales y considere el ideal generado por los polinomios. ${\displaystyle R=\mathbb {Q} [x,y]}$ ${\displaystyle I=\langle f,g\rangle }$

${\displaystyle f=x^{2}-y}$,

${\displaystyle g=x^{3}-x}$.

Reduciendo g por f , se obtiene un nuevo polinomio k tal que ${\displaystyle I=\langle f,k\rangle :}$

${\displaystyle k=g-xf=xy-x.}$

Ninguno de f y k es reducible por el otro, pero xk es reducible por f , lo que da otro polinomio en I :

${\displaystyle h=xk-(y-1)f=y^{2}-y.}$

Bajo el orden lexicográfico tenemos ${\displaystyle x>y}$

es( f ) = x ²

lt( k ) = xy

^lt ( h ) = y2

Como f , k y h pertenecen a I , y ninguno de ellos es reducible por los otros, ninguno de y es una base de Gröbner de I. ${\displaystyle \{f,k\},}$ ${\displaystyle \{f,h\},}$ ${\displaystyle \{h,k\}}$

Por otra parte, { f , k , h } es una base de Gröbner de I , ya que los S-polinomios

${\displaystyle {\begin{aligned}yf-xk&=y(x^{2}-y)-x(xy-x)=f-h\\yk-xh&=y(xy-x)-x(y^{2}-y)=0\\y^{2}f-x^{2}h&=y(yf-xk)+x(yk-xh)\end{aligned}}}$

puede reducirse a cero mediante f , k y h .

El método que se ha utilizado aquí para hallar h y k y demostrar que { f , k , h } es una base de Gröbner es una aplicación directa del algoritmo de Buchberger . Por lo tanto, se puede aplicar mecánicamente a cualquier ejemplo similar, aunque, en general, hay muchos polinomios y S-polinomios a considerar y el cálculo suele ser demasiado grande para hacerlo sin una computadora.

Propiedades y aplicaciones de las bases de Gröbner

A menos que se indique explícitamente, todos los resultados que siguen ^[3] son ​​verdaderos para cualquier ordenamiento monomial (consulte ese artículo para conocer las definiciones de los diferentes órdenes que se mencionan a continuación).

Es un error común pensar que el orden lexicográfico es necesario para algunos de estos resultados. Por el contrario, el orden lexicográfico es, casi siempre, el más difícil de calcular, y su uso hace que resulten imprácticos muchos cálculos que son relativamente fáciles con el orden lexicográfico inverso graduado (grevlex) o, cuando se necesita eliminación, el orden de eliminación (lexdeg) que restringe el uso de grevlex en cada bloque de variables.

Igualdad de ideales

Las bases de Gröbner reducidas son únicas para cualquier ideal dado y cualquier ordenamiento monomial. Por lo tanto, dos ideales son iguales si y solo si tienen la misma base de Gröbner (reducida) (por lo general, un software de bases de Gröbner siempre produce bases de Gröbner reducidas).

Pertenencia e inclusión de ideales

La reducción de un polinomio f por la base de Gröbner G de un ideal I da como resultado 0 si y sólo si f está en I . Esto permite comprobar la pertenencia de un elemento a un ideal. Otro método consiste en verificar que la base de Gröbner de G ∪{ f } es igual a G .

Para comprobar si el ideal I generado por f ₁ , ..., f _k está contenido en el ideal J , basta con comprobar que todo f _I está en J . También se puede comprobar la igualdad de las bases de Gröbner reducidas de J y J ∪ { f ₁ , ..., f _k } .

Soluciones de un sistema de ecuaciones algebraicas

Cualquier conjunto de polinomios puede considerarse un sistema de ecuaciones polinómicas al igualar los polinomios a cero. El conjunto de soluciones de un sistema de este tipo depende únicamente del ideal generado y, por lo tanto, no cambia cuando el conjunto generador dado se reemplaza por la base de Gröbner, para cualquier ordenación, del ideal generado. Una solución de este tipo, con coordenadas en un cuerpo algebraicamente cerrado que contiene los coeficientes de los polinomios, se denomina cero del ideal . En el caso habitual de coeficientes racionales , este cuerpo algebraicamente cerrado se elige como el cuerpo complejo .

Un ideal no tiene ningún cero (el sistema de ecuaciones es inconsistente ) si y sólo si 1 pertenece al ideal (este es el Nullstellensatz de Hilbert ), o, equivalentemente, si su base de Gröbner (para cualquier ordenamiento monomial) contiene 1, o, también, si la base de Gröbner reducida correspondiente es [1].

Dada la base de Gröbner G de un ideal I , este tiene solo un número finito de ceros, si y solo si, para cada variable x , G contiene un polinomio con un monomio principal que es una potencia de x (sin que ninguna otra variable aparezca en el término principal). Si este es el caso, entonces el número de ceros, contados con multiplicidad, es igual al número de monomios que no son múltiplos de ningún monomio principal de G . Este número se llama grado del ideal.

Cuando el número de ceros es finito, la base de Gröbner para un ordenamiento monomial lexicográfico proporciona, teóricamente, una solución: la primera coordenada de una solución es una raíz del máximo común divisor de los polinomios de la base que dependen sólo de la primera variable. Después de sustituir esta raíz en la base, la segunda coordenada de esta solución es una raíz del máximo común divisor de los polinomios resultantes que dependen sólo de la segunda variable, y así sucesivamente. Este proceso de resolución es sólo teórico, porque implica el cálculo del MCD y la búsqueda de raíces de polinomios con coeficientes aproximados, lo que no es posible debido a la inestabilidad numérica. Por lo tanto, se han desarrollado otros métodos para resolver sistemas polinómicos mediante bases de Gröbner (véase Sistema de ecuaciones polinómicas para más detalles).

Serie de dimensiones, grados y Hilbert

La dimensión de un ideal I en un anillo polinómico R es la dimensión de Krull del anillo R / I y es igual a la dimensión del conjunto algebraico de los ceros de I. También es igual al número de hiperplanos en posición general que se necesitan para tener una intersección con el conjunto algebraico, que es un número finito de puntos. El grado del ideal y de su conjunto algebraico asociado es el número de puntos de esta intersección finita, contados con multiplicidad. En particular, el grado de una hipersuperficie es igual al grado de su polinomio de definición.

Tanto el grado como la dimensión dependen únicamente del conjunto de los monomios principales de la base de Gröbner del ideal para cualquier ordenamiento monomial.

La dimensión es el tamaño máximo de un subconjunto S de las variables tal que no existe ningún monomio principal que dependa únicamente de las variables en S . Por lo tanto, si el ideal tiene dimensión 0, entonces para cada variable x existe un monomio principal en la base de Gröbner que es una potencia de x .

Tanto la dimensión como el grado pueden deducirse de la serie de Hilbert del ideal, que es la serie , donde es el número de monomios de grado i que no son múltiplos de ningún monomio principal en la base de Gröbner. La serie de Hilbert puede resumirse en una fracción racional ${\textstyle \sum _{i=0}^{\infty }d_{i}t^{i}}$ ${\displaystyle d_{i}}$

${\displaystyle \sum _{i=0}^{\infty }d_{i}t^{i}={\frac {P(t)}{(1-t)^{d}}},}$

donde d es la dimensión del ideal y es un polinomio tal que es el grado del ideal. ${\displaystyle P(t)}$ ${\displaystyle P(1)}$

Aunque la dimensión y el grado no dependen de la elección del ordenamiento monomial, la serie de Hilbert y el polinomio cambian cuando se cambia el ordenamiento monomial. ${\displaystyle P(t)}$

La mayoría de los sistemas de álgebra computacional que proporcionan funciones para calcular bases de Gröbner también proporcionan funciones para calcular la serie de Hilbert y, por lo tanto, también la dimensión y el grado.

Eliminación

El cálculo de las bases de Gröbner para un ordenamiento monomial de eliminación permite la teoría de eliminación computacional . Esta se basa en el siguiente teorema.

Consideremos un anillo polinomial en el que las variables se dividen en dos subconjuntos X e Y . Elijamos también un ordenamiento monomial de eliminación "eliminando" X , es decir, un ordenamiento monomial para el que se comparan dos monomios comparando primero las partes X y, en caso de igualdad solamente, considerando las partes Y . Esto implica que un monomio que contiene una variable X es mayor que todo monomio independiente de X . Si G es una base de Gröbner de un ideal I para este ordenamiento monomial, entonces es una base de Gröbner de (este ideal a menudo se denomina ideal de eliminación ). Además, consiste exactamente en los polinomios de G cuyos términos principales pertenecen a K [ Y ] (esto hace muy fácil el cálculo de , ya que solo es necesario comprobar los monomios principales). ${\displaystyle K[x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{m}]=K[X,Y],}$ ${\displaystyle G\cap K[Y]}$ ${\displaystyle I\cap K[Y]}$ ${\displaystyle G\cap K[Y]}$ ${\displaystyle G\cap K[Y]}$

Esta propiedad de eliminación tiene muchas aplicaciones, algunas descritas en las siguientes secciones.

Otra aplicación, en geometría algebraica , es que la eliminación realiza la operación geométrica de proyección de un conjunto algebraico afín en un subespacio del espacio ambiente: con la notación anterior, la ( clausura de Zariski de) la proyección del conjunto algebraico definido por el ideal I en el subespacio Y está definida por el ideal ${\displaystyle I\cap K[Y].}$

El orden lexicográfico es un orden de eliminación para cada partición. Por lo tanto, una base de Gröbner para este ordenamiento contiene mucha más información de la que normalmente se necesita. Esto puede explicar por qué las bases de Gröbner para el ordenamiento lexicográfico suelen ser las más difíciles de calcular. ${\displaystyle x_{1}>\cdots >x_{n}}$ ${\displaystyle \{x_{1},\ldots ,x_{k}\},\{x_{k+1},\ldots ,x_{n}\}.}$

Ideales entrecruzados

Si I y J son dos ideales generados respectivamente por { f ₁ , ..., f _m } y { g ₁ , ..., g _k }, entonces un único cálculo de la base de Gröbner produce una base de Gröbner de su intersección I ∩ J . Para ello, se introduce un nuevo indeterminado t , y se utiliza un ordenamiento de eliminación tal que el primer bloque contiene sólo t y el otro bloque contiene todas las demás variables (esto significa que un monomio que contiene t es mayor que todo monomio que no contiene t ). Con este ordenamiento de monomios, una base de Gröbner de I ∩ J consiste en los polinomios que no contienen t , en la base de Gröbner del ideal

${\displaystyle K=\langle tf_{1},\ldots ,tf_{m},(1-t)g_{1},\ldots ,(1-t)g_{k}\rangle .}$

En otras palabras, I ∩ J se obtiene eliminando t en K . Esto se puede demostrar observando que el ideal K consiste en los polinomios tales que y . Un polinomio de este tipo es independiente de t si y solo si a = b , lo que significa que ${\displaystyle (a-b)t+b}$ ${\displaystyle a\in I}$ ${\displaystyle b\in J}$ ${\displaystyle b\in I\cap J.}$

Implicación de una curva racional

Una curva racional es una curva algebraica que tiene un conjunto de ecuaciones paramétricas de la forma

${\displaystyle {\begin{aligned}x_{1}&={\frac {f_{1}(t)}{g_{1}(t)}}\\&\;\;\vdots \\x_{n}&={\frac {f_{n}(t)}{g_{n}(t)}},\end{aligned}}}$

donde y son polinomios univariados para 1 ≤ i ≤ n . Se puede (y se supondrá) que y son coprimos (no tienen factores comunes no constantes). ${\displaystyle f_{i}(t)}$ ${\displaystyle g_{i}(t)}$ ${\displaystyle f_{i}(t)}$ ${\displaystyle g_{i}(t)}$

La implícitación consiste en calcular las ecuaciones implícitas de dicha curva. En el caso de n = 2, es decir, para curvas planas, esto se puede calcular con la resultante . La ecuación implícita es la siguiente resultante:

${\displaystyle {\text{Res}}_{t}(g_{1}x_{1}-f_{1},g_{2}x_{2}-f_{2}).}$

La eliminación con bases de Gröbner permite implícitamente para cualquier valor de n , simplemente eliminando t en el ideal Si n = 2, el resultado es el mismo que con la resultante, si la función es inyectiva para casi todo t . En el otro caso, la resultante es una potencia del resultado de la eliminación. ${\displaystyle \langle g_{1}x_{1}-f_{1},\ldots ,g_{n}x_{n}-f_{n}\rangle .}$ ${\displaystyle t\mapsto (x_{1},x_{2})}$

Saturación

Al modelar un problema mediante ecuaciones polinómicas, a menudo se supone que algunas cantidades no son cero, para evitar casos degenerados. Por ejemplo, cuando se trabaja con triángulos , muchas propiedades se vuelven falsas si el triángulo degenera en un segmento de línea, es decir, la longitud de un lado es igual a la suma de las longitudes de los otros lados. En tales situaciones, no se puede deducir información relevante del sistema polinómico a menos que se ignoren las soluciones degeneradas. Más precisamente, el sistema de ecuaciones define un conjunto algebraico que puede tener varios componentes irreducibles , y se deben eliminar los componentes en los que las condiciones de degeneración son cero en todas partes.

Esto se hace saturando las ecuaciones con las condiciones de degeneración, lo que puede realizarse mediante la propiedad de eliminación de las bases de Gröbner.

Definición de la saturación

La localización de un anillo consiste en anexarle las inversas formales de algunos elementos. Esta sección se refiere únicamente al caso de un único elemento, o equivalentemente un número finito de elementos (anexar las inversas de varios elementos equivale a anexar la inversa de su producto). La localización de un anillo R por un elemento f es el anillo donde t es una nueva indeterminada que representa la inversa de f . La localización de un ideal I de R es el ideal de Cuando R es un anillo polinómico, el cálculo en no es eficiente debido a la necesidad de gestionar los denominadores. Por lo tanto, la localización suele sustituirse por la operación de saturación . ${\displaystyle R_{f}=R[t]/(1-ft),}$ ${\displaystyle R_{f}I}$ ${\displaystyle I_{f}.}$ ${\displaystyle R_{f}}$

Ella saturación con respecto afde un idealIenRes la imagen inversa debajo la función canónica deRaIt es el idealque consiste en todos los elementos deRcuyo producto con alguna potencia defpertenece aI. ${\displaystyle R_{f}I}$ ${\displaystyle R_{f}.}$ ${\displaystyle I:f^{\infty }=\{g\in R\mid (\exists k\in \mathbb {N} )f^{k}g\in I\}}$

Si J es el ideal generado por I y 1− ft en R [ t ], entonces se deduce que, si R es un anillo polinomial, un cálculo de base de Gröbner que elimina t produce una base de Gröbner de la saturación de un ideal por un polinomio. ${\displaystyle I:f^{\infty }=J\cap R.}$

La propiedad importante de la saturación, que asegura que elimina del conjunto algebraico definido por el ideal I los componentes irreducibles en los que el polinomio f es cero, es la siguiente: La descomposición primaria de consiste en los componentes de la descomposición primaria de I que no contienen ninguna potencia de f . ${\displaystyle I:f^{\infty }}$

Cálculo de la saturación

Una base de Gröbner de la saturación por f de un ideal polinomial generado por un conjunto finito de polinomios F , se puede obtener eliminando t, es decir, manteniendo los polinomios independientes de t en la base de Gröbner de para un ordenamiento de eliminación eliminando t . ${\displaystyle F\cup \{1-tf\},}$ ${\displaystyle F\cup \{1-tf\}}$

En lugar de utilizar F , también se puede empezar a partir de una base de Gröbner de F . El método más eficiente depende del problema. Sin embargo, si la saturación no elimina ningún componente, es decir, si el ideal es igual a su ideal saturado, calcular primero la base de Gröbner de F suele ser más rápido. Por otro lado, si la saturación elimina algunos componentes, el cálculo directo puede ser considerablemente más rápido.

Si se quiere saturar con respecto a varios polinomios o con respecto a un solo polinomio que es un producto hay tres formas de proceder que dan el mismo resultado pero pueden tener tiempos de cálculo muy diferentes (depende del problema cuál es la más eficiente). ${\displaystyle f_{1},\ldots ,f_{k}}$ ${\displaystyle f=f_{1}\cdots f_{k},}$

• Saturación mediante un único cálculo de base de Gröbner. ${\displaystyle f=f_{1}\cdots f_{k}}$
• Saturando con, luego saturando el resultado con, y así sucesivamente. ${\displaystyle f_{1},}$ ${\displaystyle f_{2},}$
• Sumando a F o a su base de Gröbner los polinomios y eliminando en un solo cálculo de base de Gröbner. ${\displaystyle 1-t_{1}f_{1},\ldots ,1-t_{k}f_{k},}$ ${\displaystyle t_{i}}$

Sentencia de nulidad efectiva

El Nullstellensatz de Hilbert tiene dos versiones. La primera afirma que un conjunto de polinomios no tiene ceros comunes en una clausura algebraica del cuerpo de los coeficientes, si y solo si 1 pertenece al ideal generado. Esto se puede comprobar fácilmente con un cálculo de la base de Gröbner, porque 1 pertenece a un ideal si y solo si 1 pertenece a la base de Gröbner del ideal, para cualquier ordenación monomial.

La segunda versión afirma que el conjunto de ceros comunes (en una clausura algebraica del cuerpo de los coeficientes) de un ideal está contenido en la hipersuperficie de los ceros de un polinomio f , si y sólo si una potencia de f pertenece al ideal. Esto puede comprobarse saturando el ideal con f ; de hecho, una potencia de f pertenece al ideal si y sólo si la saturación con f proporciona una base de Gröbner que contiene 1.

Implicación en dimensión superior

Por definición, una variedad racional afín de dimensión k puede describirse mediante ecuaciones paramétricas de la forma

${\displaystyle {\begin{aligned}x_{1}&={\frac {p_{1}}{p_{0}}}\\&\;\;\vdots \\x_{n}&={\frac {p_{n}}{p_{0}}},\end{aligned}}}$

donde son n +1 polinomios en las k variables (parámetros de la parametrización) Por lo tanto los parámetros y las coordenadas de los puntos de la variedad son ceros del ideal ${\displaystyle p_{0},\ldots ,p_{n}}$ ${\displaystyle t_{1},\ldots ,t_{k}.}$ ${\displaystyle t_{1},\ldots ,t_{k}}$ ${\displaystyle x_{1},\ldots ,x_{n}}$

${\displaystyle I=\left\langle p_{0}x_{1}-p_{1},\ldots ,p_{0}x_{n}-p_{n}\right\rangle .}$

Se podría suponer que basta con eliminar los parámetros para obtener las ecuaciones implícitas de la variedad, como se ha hecho en el caso de las curvas. Desafortunadamente, esto no siempre es así. Si las tienen un cero común (a veces llamado punto base ), cada componente irreducible del conjunto algebraico no vacío definido por las es un componente irreducible del conjunto algebraico definido por I . De ello se deduce que, en este caso, la eliminación directa de las proporciona un conjunto vacío de polinomios. ${\displaystyle p_{i}}$ ${\displaystyle p_{i}}$ ${\displaystyle t_{i}}$

Por lo tanto, si k > 1, se necesitan dos cálculos de base de Gröbner para implicar:

1. Saturar para obtener una base de Gröbner ${\displaystyle I}$ ${\displaystyle p_{0}}$ ${\displaystyle G}$
2. Elimina la forma para obtener una base de Gröbner del ideal (de las ecuaciones implícitas) de la variedad. ${\displaystyle t_{i}}$ ${\displaystyle G}$

Algoritmos e implementaciones

El algoritmo de Buchberger es el algoritmo más antiguo para calcular las bases de Gröbner. Fue ideado por Bruno Buchberger junto con la teoría de las bases de Gröbner. Es fácil de implementar, pero pronto se demostró que las implementaciones simples solo pueden resolver problemas triviales. Los principales problemas son los siguientes:

1. Incluso cuando la base de Gröbner resultante es pequeña, los polinomios intermedios pueden ser enormes. Esto hace que la mayor parte del tiempo de cálculo se dedique a la gestión de la memoria . Por lo tanto, los algoritmos especializados de gestión de memoria pueden ser una parte fundamental de una implementación eficiente.
2. Los números enteros que aparecen durante un cálculo pueden ser lo suficientemente grandes como para que resulten útiles los algoritmos de multiplicación rápida y la aritmética multimodular . Por este motivo, la mayoría de las implementaciones optimizadas utilizan GMPlibrary . Además, en las implementaciones optimizadas se utilizan la aritmética modular , el teorema del resto chino y el levantamiento de Hensel.
3. La elección de los S-polinomios a reducir y de los polinomios utilizados para reducirlos se realiza mediante heurísticas . Como en muchos problemas computacionales, las heurísticas no pueden detectar la mayoría de las simplificaciones ocultas y, si se evitan las elecciones heurísticas, se puede obtener una mejora drástica de la eficiencia del algoritmo.
4. En la mayoría de los casos, la mayoría de los polinomios S que se calculan se reducen a cero; es decir, la mayor parte del tiempo de cálculo se dedica a calcular cero.
5. El ordenamiento monomial que se necesita con mayor frecuencia para las aplicaciones (lexicográficas puras) no es el ordenamiento que conduce al cálculo más fácil, generalmente el ordenamiento degrevlex .

Para la solución de 3. se propusieron muchas mejoras, variantes y heurísticas antes de la introducción de los algoritmos F4 y F5 por Jean-Charles Faugère . Como estos algoritmos están diseñados para coeficientes enteros o con coeficientes en los enteros módulo un número primo , el algoritmo de Buchberger sigue siendo útil para coeficientes más generales.

En términos generales, el algoritmo F4 resuelve el problema 3. reemplazando muchas reducciones de polinomios S por la reducción de filas de una única matriz grande para la que se pueden utilizar métodos avanzados de álgebra lineal . Esto resuelve parcialmente el problema 4., ya que las reducciones a cero en el algoritmo de Buchberger corresponden a relaciones entre filas de la matriz que se va a reducir, y las filas cero de la matriz reducida corresponden a una base del espacio vectorial de estas relaciones.

El algoritmo F5 mejora F4 al introducir un criterio que permite reducir el tamaño de las matrices a reducir. Este criterio es casi óptimo, ya que las matrices a reducir tienen rango completo en casos suficientemente regulares (en particular, cuando los polinomios de entrada forman una secuencia regular ). Ajustar F5 para un uso general es difícil, ya que sus rendimientos dependen de un orden en los polinomios de entrada y de un equilibrio entre el incremento del grado del polinomio de trabajo y del número de polinomios de entrada que se consideran. Hasta la fecha (2022), no existe una implementación distribuida que sea significativamente más eficiente que F4, pero, sobre enteros modulares, F5 se ha utilizado con éxito para varios desafíos criptográficos ; por ejemplo, para romper el desafío HFE .

El problema 5 se ha resuelto con el descubrimiento de algoritmos de conversión de base que parten de la base de Gröbner para un ordenamiento monomial para calcular una base de Gröbner para otro ordenamiento monomial. El algoritmo FGLM es un algoritmo de conversión de base que funciona solo en el caso de dimensión cero (donde los polinomios tienen un número finito de ceros comunes complejos) y tiene una complejidad polinomial en el número de ceros comunes. Un algoritmo de conversión de base que funciona en el caso general es el algoritmo de paseo de Gröbner . ^[4] En su forma original, FGLM puede ser el paso crítico para resolver sistemas de ecuaciones polinomiales porque FGML no tiene en cuenta la escasez de matrices involucradas . Esto se ha solucionado con la introducción de algoritmos FGLM dispersos . ^[5]

La mayoría de los sistemas de álgebra computacional de propósito general tienen implementaciones de uno o varios algoritmos para bases de Gröbner, a menudo también embebidos en otras funciones, como para resolver sistemas de ecuaciones polinómicas o para simplificar funciones trigonométricas; este es el caso, por ejemplo, de CoCoA , GAP , Macaulay 2 , Magma , Maple , Mathematica , SINGULAR , SageMath y SymPy . Cuando F4 está disponible, generalmente es mucho más eficiente que el algoritmo de Buchberger. Las técnicas de implementación y las variantes algorítmicas no siempre están documentadas, aunque pueden tener un efecto dramático en la eficiencia.

Las implementaciones de F4 y (sparse)-FGLM están incluidas en la biblioteca Msolve . ^[6] Además de los algoritmos de Gröbner, Msolve contiene algoritmos rápidos para el aislamiento de raíces reales y combina todas estas funciones en un algoritmo para las soluciones reales de sistemas de ecuaciones polinómicas que supera drásticamente al otro software para este problema (Maple y Magma). ^[6] Msolve está disponible en GitHub y está interconectado con Julia , Maple y SageMath; esto significa que Msolve se puede utilizar directamente desde estos entornos de software.

Complejidad

La complejidad de los cálculos de la base de Gröbner se evalúa comúnmente en términos del número n de variables y el grado máximo d de los polinomios de entrada.

En el peor de los casos, el parámetro principal de la complejidad es el grado máximo de los elementos de la base de Gröbner reducida resultante. Más precisamente, si la base de Gröbner contiene un elemento de un grado grande D , este elemento puede contener términos distintos de cero cuyo cálculo requiere un tiempo de Por otro lado, si todos los polinomios en la base de Gröbner reducida un ideal homogéneo tienen un grado de como máximo D , la base de Gröbner se puede calcular mediante álgebra lineal en el espacio vectorial de polinomios de grado menor que 2 D , que tiene una dimensión ^[1] Por lo tanto, la complejidad de este cálculo es ${\displaystyle \Omega (D^{n})}$ ${\displaystyle \Omega (D^{n})>D^{\Omega (n)}.}$ ${\displaystyle O(D^{n}).}$ ${\displaystyle O(D^{n})^{O(1)}=D^{O(n)}.}$

La complejidad del peor caso de un cálculo de base de Gröbner es doblemente exponencial en n . Más precisamente, la complejidad está limitada superiormente por un polinomio en Usando la notación o pequeña , está limitada por Por otro lado, se han dado ejemplos de bases de Gröbner reducidas que contienen polinomios de grado o que contienen elementos. Como cada algoritmo para calcular una base de Gröbner debe escribir su resultado, esto proporciona un límite inferior de la complejidad. ${\textstyle d^{2^{n}}.}$ ${\textstyle d^{2^{n+o(n)}}.}$ ${\textstyle d^{2^{\Omega (n)}},}$ ${\textstyle d^{2^{\Omega (n)}}}$

La base de Gröbner es EXPSPACE-completa . ^[7]

Generalizaciones

El concepto y los algoritmos de las bases de Gröbner se han generalizado a submódulos de módulos libres sobre un anillo polinómico. De hecho, si L es un módulo libre sobre un anillo R , entonces se puede considerar la suma directa como un anillo definiendo el producto de dos elementos de L como 0 . Este anillo se puede identificar con , donde es una base de L . Esto permite identificar un submódulo de L generado por con el ideal de generado por y los productos , . Si R es un anillo polinómico, esto reduce la teoría y los algoritmos de las bases de Gröbner de módulos a la teoría y los algoritmos de las bases de Gröbner de ideales. ${\displaystyle R\oplus L}$ ${\displaystyle R[e_{1},\ldots ,e_{l}]/\left\langle \{e_{i}e_{j}|1\leq i\leq j\leq l\}\right\rangle }$ ${\displaystyle e_{1},\ldots ,e_{l}}$ ${\displaystyle g_{1},\ldots ,g_{k}}$ ${\displaystyle R[e_{1},\ldots ,e_{l}]}$ ${\displaystyle g_{1},\ldots ,g_{k}}$ ${\displaystyle e_{i}e_{j}}$ ${\displaystyle 1\leq i\leq j\leq l}$

El concepto y los algoritmos de las bases de Gröbner también se han generalizado a ideales sobre varios anillos, conmutativos o no, como anillos polinomiales sobre un anillo ideal principal o álgebras de Weyl .

Áreas de aplicación

Códigos de corrección de errores

La base de Gröbner se ha aplicado en la teoría de códigos de corrección de errores para la decodificación algebraica. Mediante el uso del cálculo de la base de Gröbner en varias formas de ecuaciones de corrección de errores, se desarrollaron métodos de decodificación para corregir errores de códigos cíclicos, ^[8] códigos de variedad afín, ^[9] códigos algebraicos-geométricos e incluso códigos de bloques lineales generales. ^[10] La aplicación de la base de Gröbner en la decodificación algebraica sigue siendo un área de investigación de la teoría de codificación de canales.

Véase también

• Lema del diamante de Bergman , una extensión de las bases de Gröbner a anillos no conmutativos
• Base más grave
• Base de Janet
• Cadenas regulares , una forma alternativa de representar conjuntos algebraicos

Referencias

1. Lazard, Daniel (1983). "Bases de Gröbner, eliminación gaussiana y resolución de sistemas de ecuaciones algebraicas". Computer Algebra . Lecture Notes in Computer Science. Vol. 162. págs. 146–156. doi :10.1007/3-540-12868-9_99. ISBN 978-3-540-12868-7.
2. Renschuch, Bodo; Roloff, Hartmut; Rasputin, Georgij G.; Abramson, Michael (junio de 2003). "Contribuciones a la teoría de polinomios ideales constructivos XXIII: trabajos olvidados del matemático de Leningrado NM Gjunter sobre la teoría de polinomios ideales" (PDF) . SIGSAM Bull . 37 (2): 35–48. doi :10.1145/944567.944569. S2CID  1819694.
3. Cox, David A .; Little, John; O'Shea, Donal (1997). Ideales, variedades y algoritmos: Introducción a la geometría algebraica computacional y al álgebra conmutativa . Springer. ISBN 0-387-94680-2.
4. Collart, Stéphane; Kalkbrener, Michael; Mall, Daniel (1997). "Conversión de bases con el recorrido de Gröbner". Journal of Symbolic Computation . 24 (3–4). Elsevier: 465–469. doi : 10.1006/jsco.1996.0145 .
5. Faugère, Jean-Charles ; Chenqi, Mou (2017). "Algoritmos FGLM dispersos". Revista de computación simbólica . 80 . Elsevier: 538–569. arXiv : 1304.1238 . doi : 10.1016/j.jsc.2016.07.025 . S2CID  149627.
6. Berthomieu \first1=Jérémy; Eder, Christian; Safey El Din, Mohab (2021). Msolve: una biblioteca para resolver sistemas polinomiales. Simposio internacional sobre computación simbólica y algebraica de 2021. 46.º Simposio internacional sobre computación simbólica y algebraica. San Petersburgo, Rusia. arXiv : 2104.03572 . doi :10.1145/3452143.3465545.{{cite conference}}: CS1 maint: numeric names: authors list (link)
7. Mayr, Ernst W. (septiembre de 1997), "Algunos resultados de complejidad para ideales polinomiales", Journal of Complexity , 13 (3): 303–325, doi : 10.1006/jcom.1997.0447
8. Chen, X.; Reed, IS; Helleseth, T.; Truong, T.K. (1994). "Uso de bases de Gröbner para decodificar códigos cíclicos binarios hasta la distancia mínima verdadera". IEEE Transactions on Information Theory . 40 (5): 1654–61. doi :10.1109/18.333885.
9. Fitzgerald, J.; Lax, RF (1998). "Descodificación de códigos de variedad afín utilizando bases de Gröbner". Diseños, códigos y criptografía . 13 (2): 147–158. doi :10.1023/A:1008274212057. S2CID  2515114.
10. Bulygin, S.; Pellikaan, R. (2009). "Decodificación de códigos de corrección de errores lineales hasta la mitad de la distancia mínima con bases de Gröbner". Bases de Gröbner, codificación y criptografía . Springer . págs. 361–5. ISBN 978-3-540-93805-7.

Lectura adicional

• Adams, William W.; Loustaunau, Philippe (1994). Introducción a las bases de Gröbner . Estudios de posgrado en matemáticas . Vol. 3. Sociedad Americana de Matemáticas . ISBN. 0-8218-3804-0.
• Li, Huishi (2011). Bases de Gröbner en la teoría de anillos . World Scientific . ISBN 978-981-4365-13-0.
• Becker, Thomas; Weispfenning, Volker (1998). Bases de Gröbner: un enfoque computacional para el álgebra conmutativa . Textos de posgrado en matemáticas. Vol. 141. Springer. ISBN 0-387-97971-9.
• Buchberger, Bruno (1965). Un algoritmo para hallar los elementos base del anillo de clases de residuos de un polinomio ideal de dimensión cero (PDF) (PhD). Universidad de Innsbruck. — (2006). "Tesis doctoral de Bruno Buchberger de 1965: Un algoritmo para encontrar los elementos base del anillo de clases de residuos de un ideal polinomial de dimensión cero". Journal of Symbolic Computation . 41 (3–4). Traducido por Abramson, M.: 471–511. doi : 10.1016/j.jsc.2005.09.007 . [Esta es la tesis de Buchberger inventando las bases de Gröbner.]
• Buchberger, Bruno (1970). "Un criterio algorítmico para la resolubilidad de un sistema de ecuaciones algebraicas" (PDF) . Aequationes Mathematicae . 4 : 374–383. doi :10.1007/BF01844169. S2CID  189834323. (Esta es la publicación en revista de la tesis de Buchberger.) Burchberger, B.; Winkler, F., eds. (26 de febrero de 1998). "Un criterio algorítmico para la resolubilidad de un sistema de ecuaciones algebraicas". Bases y aplicaciones de Gröbner . Serie de notas de conferencias de la London Mathematical Society. Vol. 251. Cambridge University Press. págs. 535–545. ISBN 978-0-521-63298-0.
• Buchberger, Bruno; Kauers, Manuel (2010). "Bases de Gröbner". Scholarpedia . 5 (10): 7763. Bibcode :2010SchpJ...5.7763B. doi : 10.4249/scholarpedia.7763 .
• Froberg, Ralf (1997). Introducción a las bases de Gröbner . Wiley. ISBN 0-471-97442-0.
• Sturmfels, Bernd (noviembre de 2005). "¿Qué es... una base de Gröbner?" (PDF) . Notices of the American Mathematical Society . 52 (10): 1199–1200, una breve introducción.{{cite journal}}: CS1 maint: postscript (link)
• Shirshov, Anatoliĭ I. (1999). "Ciertos problemas algorítmicos para álgebras de Lie" (PDF) . Boletín ACM SIGSAM . 33 (2): 3–6. doi :10.1145/334714.334715. S2CID  37070503.(traducido de Sibirsk. Mat. Zh. Siberian Mathematics Journal 3 (1962), 292–296).
• Aschenbrenner, Matthias ; Hillar, Christopher (2007). "Generación finita de ideales simétricos". Transactions of the American Mathematical Society . 359 (11): 5171–92. arXiv : math/0411514 . doi : 10.1090/S0002-9947-07-04116-5 . S2CID  5656701.(sobre bases de Gröbner de dimensión infinita para anillos polinomiales en infinitos indeterminados).

Enlaces externos

• Implementación del algoritmo F4 por parte de Faugère
• "Base de Gröbner", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Buchberger, B. (2003). "Bases de Gröbner: una breve introducción para teóricos de sistemas" (PDF) . En Moreno-Diaz, R.; Buchberger, B.; Freire, J. (eds.). Teoría de sistemas asistidos por ordenador — EUROCAST 2001: una selección de artículos del 8º taller internacional sobre teoría de sistemas asistidos por ordenador. Springer. pp. 1–19. ISBN. 978-3-540-45654-4.
• Buchberger, B.; Zapletal, A. "Bibliografía de las bases de Gröbner".
• Página de tiempos comparativos para el software de bases de Gröbner
• Profesor Bruno Buchberger Bruno Buchberger
• Weisstein, Eric W. "Base Gröbner". MundoMatemático .
• Introducción a la base de Gröbner en Scholarpedia