El argumento de indispensabilidad de Quine-Putnam [a] es un argumento en la filosofía de las matemáticas a favor de la existencia de objetos matemáticos abstractos como números y conjuntos, una postura conocida como platonismo matemático . Debe su nombre a los filósofos Willard Quine y Hilary Putnam , y es uno de los argumentos más importantes en la filosofía de las matemáticas.
Aunque algunos elementos del argumento de la indispensabilidad pueden haberse originado con pensadores como Gottlob Frege y Kurt Gödel , el desarrollo del argumento por parte de Quine fue único al introducir en él varias de sus posiciones filosóficas, como el naturalismo , el holismo confirmacional y el criterio de compromiso ontológico . Putnam dio al argumento de Quine su primera formulación detallada en su libro de 1971 Filosofía de la lógica . Sin embargo, más tarde llegó a estar en desacuerdo con varios aspectos del pensamiento de Quine y formuló su propio argumento de la indispensabilidad basado en el argumento de la inexistencia de milagros en la filosofía de la ciencia . Una forma estándar del argumento en la filosofía contemporánea se le atribuye a Mark Colyvan ; aunque está influenciado tanto por Quine como por Putnam, difiere en formas importantes de sus formulaciones. Se presenta en la Enciclopedia de Filosofía de Stanford : [2]
Los nominalistas , filósofos que rechazan la existencia de objetos abstractos, han argumentado en contra de ambas premisas de este argumento. Un influyente argumento de Hartry Field afirma que las entidades matemáticas son prescindibles para la ciencia. Este argumento ha sido apoyado por intentos de demostrar que las teorías científicas y matemáticas pueden reformularse para eliminar todas las referencias a las entidades matemáticas. Otros filósofos, incluidos Penelope Maddy , Elliott Sober y Joseph Melia , han argumentado que no necesitamos creer en todas las entidades que son indispensables para la ciencia. Los argumentos de estos escritores inspiraron una nueva versión explicativa del argumento , que Alan Baker y Mark Colyvan apoyan, que sostiene que las matemáticas son indispensables para explicaciones científicas específicas, así como para teorías completas.
En su artículo de 1973 "La verdad matemática", Paul Benacerraf planteó un problema para la filosofía de las matemáticas . [b] Según Benacerraf, oraciones matemáticas como "dos es un número primo" implican la existencia de objetos matemáticos . [5] Él respaldó esta afirmación con la idea de que las matemáticas no deberían tener su propia semántica especial , o en otras palabras, el significado de las oraciones matemáticas debería seguir las mismas reglas que las oraciones no matemáticas. Por ejemplo, según este razonamiento, si la oración "Marte es un planeta" implica la existencia del planeta Marte, entonces la oración "dos es un número primo" también debería implicar la existencia del número dos. [6] Pero según Benacerraf, si existieran objetos matemáticos, serían incognoscibles. [5] Esto se debe a que los objetos matemáticos, si existen, son objetos abstractos : objetos que no pueden hacer que sucedan cosas y que no tienen ubicación en el espacio y el tiempo. [7] Benacerraf argumentó, sobre la base de la teoría causal del conocimiento , que sería imposible saber acerca de tales objetos porque no pueden entrar en contacto causal con nosotros. [c] [9] Esto se llama el problema epistemológico de Benacerraf porque concierne a la epistemología de las matemáticas, es decir, cómo llegamos a saber lo que hacemos acerca de las matemáticas. [10]
La filosofía de las matemáticas se divide en dos corrientes principales: el platonismo y el nominalismo . El platonismo sostiene que existen objetos matemáticos abstractos como los números y los conjuntos, mientras que el nominalismo niega su existencia. [11] Cada una de estas perspectivas se enfrenta a problemas debido al problema planteado por Benacerraf. Como el nominalismo rechaza la existencia de objetos matemáticos, no se enfrenta a ningún problema epistemológico, pero sí a problemas relacionados con la idea de que las matemáticas no deberían tener su propia semántica especial. El platonismo no se enfrenta a problemas relacionados con la mitad semántica del dilema, pero tiene dificultades para explicar cómo podemos tener algún conocimiento sobre los objetos matemáticos. [12]
El argumento de indispensabilidad tiene como objetivo superar el problema epistemológico planteado contra el platonismo al proporcionar una justificación para la creencia en objetos matemáticos abstractos. [13] Es parte de una amplia clase de argumentos de indispensabilidad que se aplican más comúnmente en la filosofía de las matemáticas, pero que también incluye argumentos en la filosofía del lenguaje y la ética . [14] En el sentido más general, los argumentos de indispensabilidad tienen como objetivo respaldar su conclusión basándose en la afirmación de que la verdad de la conclusión es indispensable o necesaria para un determinado propósito. [15] Cuando se aplican en el campo de la ontología —el estudio de lo que existe— ejemplifican una estrategia quineana para establecer la existencia de entidades controvertidas que no pueden investigarse directamente. Según esta estrategia, la indispensabilidad de estas entidades para formular una teoría de otras entidades menos controvertidas cuenta como evidencia de su existencia. [16] En el caso de la filosofía de las matemáticas, la indispensabilidad de las entidades matemáticas para formular teorías científicas se toma como evidencia de la existencia de esas entidades matemáticas. [17]
Mark Colyvan presenta el argumento en la Enciclopedia de Filosofía de Stanford en la siguiente forma: [2]
Aquí, un compromiso ontológico con una entidad es un compromiso de creer que esa entidad existe. [18] La primera premisa se basa en dos supuestos fundamentales: el naturalismo y el holismo confirmacional . Según el naturalismo, deberíamos mirar a nuestras mejores teorías científicas para determinar qué tenemos la mejor razón para creer que existe. [19] Quine resumió el naturalismo como "el reconocimiento de que es dentro de la ciencia misma, y no en alguna filosofía previa, que la realidad debe ser identificada y descrita". [20] El holismo confirmacional es la visión de que las teorías científicas no pueden confirmarse de forma aislada y deben confirmarse como un todo. Por lo tanto, según el holismo confirmacional, si debemos creer en la ciencia, entonces debemos creer en toda la ciencia, incluida cualquiera de las matemáticas que se asumen en nuestras mejores teorías científicas. [19] El argumento está dirigido principalmente a los nominalistas que son realistas científicos , ya que intenta justificar la creencia en entidades matemáticas de una manera similar a la justificación de la creencia en entidades teóricas como los electrones o los quarks ; Quine sostuvo que dichos nominalistas tienen un "doble estándar" con respecto a la ontología. [2]
El argumento de la indispensabilidad difiere de otros argumentos a favor del platonismo porque sólo defiende la creencia en las partes de las matemáticas que son indispensables para la ciencia. No justifica necesariamente la creencia en las partes más abstractas de la teoría de conjuntos, que Quine llamó "recreación matemática... sin derechos ontológicos". [21] Algunos filósofos infieren del argumento que el conocimiento matemático es a posteriori porque implica que las verdades matemáticas sólo pueden establecerse mediante la confirmación empírica de las teorías científicas para las que son indispensables. Esto también indica que las verdades matemáticas son contingentes, ya que las verdades conocidas empíricamente son generalmente contingentes. Tal posición es controvertida porque contradice la visión tradicional del conocimiento matemático como conocimiento a priori de verdades necesarias . [22]
Si bien el argumento original de Quine es un argumento a favor del platonismo, también se pueden construir argumentos de indispensabilidad para defender la afirmación más débil del realismo oracional: la afirmación de que la teoría matemática es objetivamente verdadera. Esta es una afirmación más débil porque no implica necesariamente que existan objetos matemáticos abstractos. [23] [d]
La segunda premisa del argumento de la indispensabilidad establece que los objetos matemáticos son indispensables para nuestras mejores teorías científicas. En este contexto, la indispensabilidad no es lo mismo que la ineliminabilidad porque cualquier entidad puede eliminarse de un sistema teórico si se realizan los ajustes apropiados a las otras partes del sistema. [25] La indispensabilidad, en cambio, significa que una entidad no puede eliminarse sin reducir el atractivo de la teoría. El atractivo de la teoría puede evaluarse en términos de virtudes teóricas como el poder explicativo , la adecuación empírica y la simplicidad . [26] Además, si una entidad es prescindible para una teoría, se puede formular una teoría equivalente sin ella. [27] Este es el caso, por ejemplo, si cada oración de una teoría es una paráfrasis de una oración de otra o si las dos teorías predicen las mismas observaciones empíricas. [28]
Según la Stanford Encyclopedia of Philosophy , uno de los argumentos más influyentes contra el argumento de la indispensabilidad proviene de Hartry Field . [29] Rechaza la afirmación de que los objetos matemáticos son indispensables para la ciencia; [30] Field ha apoyado este argumento reformulando o "nominalizando" las teorías científicas para que no se refieran a objetos matemáticos. [31] Como parte de este proyecto, Field ha ofrecido una reformulación de la física newtoniana en términos de las relaciones entre puntos del espacio-tiempo. En lugar de referirse a distancias numéricas, la reformulación de Field utiliza relaciones como "entre" y "congruente" para recuperar la teoría sin implicar la existencia de números. [32] John Burgess y Mark Balaguer han tomado medidas para extender este proyecto nominalizador a áreas de la física moderna , incluida la mecánica cuántica . [33] Filósofos como David Malament y Otávio Bueno disputan si tales reformulaciones son exitosas o incluso posibles, particularmente en el caso de la mecánica cuántica. [34]
La alternativa de Field al platonismo es el ficcionalismo matemático , según el cual las teorías matemáticas son falsas porque se refieren a objetos abstractos que no existen. [35] Como parte de su argumento contra el argumento de la indispensabilidad, Field ha tratado de explicar cómo es posible que la ciencia utilice enunciados matemáticos falsos sin que las predicciones científicas sean falsas. [36] Su argumento se basa en la idea de que las matemáticas son conservadoras . Una teoría matemática es conservadora si, cuando se combina con una teoría científica, no implica nada sobre el mundo físico que la teoría científica por sí sola no tendría ya. [37] Esto explica cómo es posible que las matemáticas sean utilizadas por teorías científicas sin que las predicciones de la ciencia sean falsas. Además, Field ha intentado especificar exactamente cómo las matemáticas son útiles en la aplicación. [29] Field piensa que las matemáticas son útiles para la ciencia porque el lenguaje matemático proporciona una abreviatura útil para hablar de sistemas físicos complejos. [33]
Otra forma de negar que las entidades matemáticas son indispensables para la ciencia es reformular las teorías matemáticas para que no impliquen la existencia de objetos matemáticos. Charles Chihara , Geoffrey Hellman y Putnam han propuesto reformulaciones modales de las matemáticas que reemplazan todas las referencias a objetos matemáticos con afirmaciones sobre posibilidades. [33]
El naturalismo que subyace al argumento de la indispensabilidad es una forma de naturalismo metodológico que afirma la primacía del método científico para determinar la verdad. [38] En otras palabras, según el naturalismo de Quine, nuestras mejores teorías científicas son la mejor guía de lo que existe. [19] Esta forma de naturalismo rechaza la idea de que la filosofía precede y en última instancia justifica la creencia en la ciencia, y sostiene en cambio que la ciencia y la filosofía son continuas entre sí como parte de una única investigación unificada del mundo. [39] Como tal, esta forma de naturalismo excluye la idea de una filosofía previa que pueda anular los compromisos ontológicos de la ciencia. [40] Esto contrasta con las formas metafísicas del naturalismo , que descartan la existencia de objetos abstractos porque no son físicos. [41] Un ejemplo de tal naturalismo es apoyado por David Armstrong . Sostiene un principio llamado principio eleático , que establece que solo existen entidades causales y no hay entidades no causales. [42] El naturalismo de Quine afirma que dicho principio no puede utilizarse para revocar el compromiso ontológico de nuestras mejores teorías científicas con las entidades matemáticas porque los principios filosóficos no pueden prevalecer sobre la ciencia. [43]
Me da risa pensar en lo presuntuoso que sería rechazar las matemáticas por razones filosóficas. ¿Qué os parecería tener la tarea de decirles a los matemáticos que deben cambiar sus métodos y abjurar de innumerables errores ahora que la filosofía ha descubierto que no hay clases? ¿Podéis decirles, con cara seria, que sigan el argumento filosófico adondequiera que les lleve? Si ponen en tela de juicio vuestras credenciales, ¿os jactaréis de otros grandes descubrimientos de la filosofía: que el movimiento es imposible , que no se puede concebir un Ser mayor que el cual no se puede concebir que no exista , ... y así sucesivamente, y así sucesivamente, hasta la saciedad? ¡Yo no!
David Lewis, Partes de las clases [44]
Quine sostuvo que su naturalismo era un supuesto fundamental, pero filósofos posteriores han aportado argumentos para apoyarlo. Los argumentos más comunes en apoyo del naturalismo quineano son los argumentos de trayectoria. Estos son argumentos que apelan a la trayectoria exitosa de la ciencia en comparación con la filosofía y otras disciplinas. [45] David Lewis hizo famoso este argumento en un pasaje de su libro de 1991 Parts of Classes , ridiculizando la trayectoria de la filosofía en comparación con las matemáticas y argumentando que la idea de que la filosofía anule a la ciencia es absurda. [46] Los críticos del argumento de la trayectoria han argumentado que va demasiado lejos, desacreditando por completo los argumentos y métodos filosóficos, y cuestionan la idea de que se pueda juzgar uniformemente que la filosofía ha tenido una mala trayectoria. [47]
El naturalismo de Quine también ha sido criticado por Penelope Maddy por contradecir la práctica matemática. [48] Según el argumento de la indispensabilidad, las matemáticas están subordinadas a las ciencias naturales en el sentido de que su legitimidad depende de ellas. [49] Pero Maddy sostiene que los matemáticos no parecen creer que su práctica esté restringida de ninguna manera por la actividad de las ciencias naturales. Por ejemplo, los argumentos de los matemáticos sobre los axiomas de la teoría de conjuntos de Zermelo-Fraenkel no apelan a sus aplicaciones a las ciencias naturales. De manera similar, Charles Parsons ha sostenido que las verdades matemáticas parecen inmediatamente obvias de una manera que sugiere que no dependen de los resultados de nuestras mejores teorías. [50]
El holismo confirmatorio es la visión de que las teorías e hipótesis científicas no pueden confirmarse de forma aislada y deben confirmarse en conjunto como parte de un conjunto más amplio de teorías. [51] Un ejemplo de esta idea proporcionada por Michael Resnik es la hipótesis de que un observador verá que el aceite y el agua se separan si se juntan porque no se mezclan. Esta hipótesis no puede confirmarse de forma aislada porque se basa en suposiciones como la ausencia de cualquier sustancia química que interfiera con su separación y que los ojos del observador funcionan lo suficientemente bien como para observar la separación. [52] Debido a que las teorías matemáticas también son asumidas por las teorías científicas, el holismo confirmatorio implica que las confirmaciones empíricas de las teorías científicas también respaldan estas teorías matemáticas. [53]
Según un contraargumento de Maddy, las tesis del naturalismo y el holismo confirmacional que conforman la primera premisa del argumento de la indispensabilidad están en tensión entre sí. Maddy dijo que el naturalismo nos dice que debemos respetar los métodos utilizados por los científicos como el mejor método para descubrir la verdad, pero los científicos no actúan como si debiéramos creer en todas las entidades que son indispensables para la ciencia. [54] Para ilustrar este punto, Maddy usa el ejemplo de la teoría atómica ; afirma que a pesar de que el átomo era indispensable para las mejores teorías de los científicos en 1860, su realidad no fue aceptada universalmente hasta 1913, cuando se sometieron a una prueba experimental directa. [55] Maddy, y otros como Mary Leng , también apelan al hecho de que los científicos usan idealizaciones matemáticas (como suponer que los cuerpos de agua son infinitamente profundos) sin tener en cuenta si son verdaderas. [56] Según Maddy, esto indica que los científicos no ven el uso indispensable de las matemáticas para la ciencia como justificación para la creencia en las matemáticas o en las entidades matemáticas. En general, Maddy dijo que deberíamos apoyar el naturalismo y rechazar el holismo confirmacional, lo que significa que no necesitamos creer en todas las entidades que son indispensables para la ciencia. [29]
Otro contraargumento de Elliott Sober sostiene que las teorías matemáticas no se prueban de la misma manera que las teorías científicas. Sober afirma que las teorías científicas compiten con alternativas para encontrar cuál teoría tiene el mayor respaldo empírico. Pero no hay alternativas con las que la teoría matemática pueda competir porque todas las teorías científicas comparten el mismo núcleo matemático. Como resultado, según Sober, las teorías matemáticas no comparten el respaldo empírico de nuestras mejores teorías científicas, por lo que deberíamos rechazar el holismo confirmatorio. [57]
Desde que se han planteado estos contraargumentos, varios filósofos (entre ellos Resnik, Alan Baker , Patrick Dieveney, David Liggins , Jacob Busch y Andrea Sereni) han sostenido que el holismo confirmatorio puede eliminarse del argumento. [58] Por ejemplo, Resnik ha ofrecido un argumento pragmático de indispensabilidad centrado menos en la noción de evidencia y más en la importancia práctica de las matemáticas para realizar investigaciones científicas. [59]
Otra parte clave del argumento es el concepto de compromiso ontológico . Un compromiso ontológico con una entidad es un compromiso de creer que esa entidad existe. Puede dividirse en dos componentes: los compromisos mantenidos por las personas individuales y los compromisos de las teorías en las que creen. Quine creía que deberíamos estar comprometidos con las mismas entidades con las que están comprometidas nuestras mejores teorías científicas. [60] Formuló un "criterio de compromiso ontológico", que apunta a descubrir los compromisos de nuestras mejores teorías traduciéndolas o "regimentándolas" del lenguaje ordinario a la lógica de primer orden . [61] En el lenguaje ordinario, Quine creía que el término "hay" debe conllevar un compromiso ontológico; decir "hay" algo significa que esa cosa existe. [e] [63] Y para Quine, el cuantificador existencial en la lógica de primer orden era el equivalente natural de "hay". Por lo tanto, al traducir las teorías científicas a la lógica de primer orden, el criterio de Quine toma los compromisos ontológicos de la teoría como todos los objetos sobre los que la teoría regimentada cuantifica . [61]
Quine pensaba que era importante traducir nuestras mejores teorías científicas a la lógica de primer orden porque el lenguaje ordinario es ambiguo, mientras que la lógica puede hacer que los compromisos de una teoría sean más precisos. Traducir teorías a la lógica de primer orden también tiene ventajas sobre traducirlas a lógicas de orden superior como la lógica de segundo orden . Si bien la lógica de segundo orden tiene el mismo poder expresivo que la lógica de primer orden, carece de algunas de las fortalezas técnicas de la lógica de primer orden, como la completitud y la compacidad . La lógica de segundo orden también permite la cuantificación sobre propiedades como la "rojez", pero si tenemos un compromiso ontológico con las propiedades es controvertido. [18] Según Quine, tal cuantificación es simplemente agramatical. [64]
Jody Azzouni ha objetado el criterio de compromiso ontológico de Quine, diciendo que el cuantificador existencial en la lógica de primer orden no siempre conlleva un compromiso ontológico. [65] Según Azzouni, el equivalente en lenguaje ordinario de la cuantificación existencial "hay" se usa a menudo en oraciones sin implicar un compromiso ontológico. En particular, Azzouni señala el uso de "hay" cuando se hace referencia a objetos ficticios en oraciones como "hay detectives ficticios que son admirados por algunos detectives reales". [66] Según Azzouni, para que tengamos un compromiso ontológico con una entidad, debemos tener el nivel adecuado de acceso epistémico a ella. Esto significa, por ejemplo, que debe superar algunas cargas epistémicas para que podamos postularla. Pero según Azzouni, las entidades matemáticas son "meras postulaciones" que pueden ser postuladas por cualquiera en cualquier momento "simplemente escribiendo un conjunto de axiomas", por lo que no necesitamos tratarlas como reales. [67]
Las presentaciones más modernas del argumento no necesariamente aceptan el criterio de compromiso ontológico de Quine y pueden permitir que los compromisos ontológicos se determinen directamente a partir del lenguaje ordinario. [68] [f]
Un problema con el argumento, planteado por Joseph Melia , es que no explica el papel de las matemáticas en la ciencia. Según Melia, solo necesitamos creer en las matemáticas si son indispensables para la ciencia de la manera correcta. En particular, deben ser indispensables para las explicaciones científicas. [70] Pero según Melia, las matemáticas juegan un papel puramente representativo en la ciencia, simplemente "[hacen] más cosas que se puedan decir sobre objetos concretos". [71] Sostiene que es legítimo retirar el compromiso con las matemáticas por esta razón, citando un fenómeno lingüístico que él llama "comadreja". Esto es cuando una persona hace una declaración y luego retira algo implícito en esa declaración. Un ejemplo de comadreja utilizada para expresar información en un contexto cotidiano es "Todos los que vinieron al seminario tenían un folleto. Pero la persona que llegó tarde no lo recibió". [72] Aquí, se transmite información aparentemente contradictoria, pero leída con caridad simplemente dice que todos, excepto la persona que llegó tarde, recibieron un folleto. [72] De manera similar, según Melia, aunque las matemáticas son indispensables para la ciencia, "casi todos los científicos... niegan que existan objetos matemáticos", lo que implica que se está eludiendo el compromiso con los objetos matemáticos. [73] Para Melia, tal elusión es aceptable porque las matemáticas no juegan un papel genuinamente explicativo en la ciencia. [74]
Inspirados tanto por los argumentos contra el holismo confirmatorio [75] como por el argumento de Melia de que podemos suspender la creencia en las matemáticas si no juegan un papel genuinamente explicativo en la ciencia, [76] Colyvan y Baker han defendido una versión explicativa del argumento de la indispensabilidad . [77] [g] Esta versión del argumento intenta eliminar la dependencia del holismo confirmatorio reemplazándola por una inferencia a la mejor explicación . Afirma que estamos justificados en creer en objetos matemáticos porque aparecen en nuestras mejores explicaciones científicas, no porque hereden el apoyo empírico de nuestras mejores teorías. [80] La Internet Encyclopedia of Philosophy la presenta de la siguiente forma: [77]
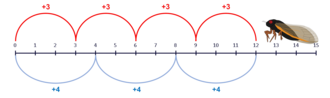
Un ejemplo de la indispensabilidad explicativa de las matemáticas presentado por Baker es la cigarra periódica , un tipo de insecto que suele tener ciclos de vida de 13 o 17 años. Se plantea la hipótesis de que esto es una ventaja evolutiva porque 13 y 17 son números primos . Como los números primos no tienen factores no triviales, esto significa que es menos probable que los depredadores puedan sincronizarse con los ciclos de vida de las cigarras. Baker dijo que esta es una explicación en la que las matemáticas, específicamente la teoría de números , juegan un papel clave para explicar un fenómeno empírico. [81]
Otros ejemplos importantes son las explicaciones de la estructura hexagonal de los panales de abejas y la imposibilidad de cruzar los siete puentes de Königsberg sólo una vez en un paseo por la ciudad. [82] La principal respuesta a esta forma de argumento, que han adoptado filósofos como Melia, Chris Daly, Simon Langford y Juha Saatsi, es negar que existan explicaciones genuinamente matemáticas de los fenómenos empíricos, enmarcando en cambio el papel de las matemáticas como representacional o indicial. [83]

El argumento se asocia históricamente con Willard Quine y Hilary Putnam , pero se puede rastrear hasta pensadores anteriores como Gottlob Frege y Kurt Gödel . En sus argumentos contra el formalismo matemático —una visión que compara las matemáticas con un juego como el ajedrez con reglas sobre cómo se pueden manipular símbolos matemáticos como "2"— Frege dijo en 1893 que "es solo la aplicabilidad lo que eleva la aritmética de un juego al rango de ciencia". [84] Gödel, en un artículo de 1947 sobre los axiomas de la teoría de conjuntos , dijo que si un nuevo axioma tuviera suficientes consecuencias verificables, "tendría que ser aceptado al menos en el mismo sentido que cualquier teoría física bien establecida". [85] Los argumentos de Frege y Gödel difieren del argumento de indispensabilidad de Quine porque carecen de características como el naturalismo y la subordinación de la práctica, lo que lleva a algunos filósofos, incluido Pieranna Garavaso , a decir que no son ejemplos genuinos del argumento de indispensabilidad. [86]
Mientras desarrollaba su visión filosófica del holismo confirmacional, Quine fue influenciado por Pierre Duhem . [87] A principios del siglo XX, Duhem defendió la ley de la inercia de los críticos que decían que carecía de contenido empírico y era infalsable . [52] Estos críticos basaron esta afirmación en el hecho de que la ley no hace ninguna predicción observable sin postular algún marco de referencia observacional y que las instancias de falsificación siempre se pueden evitar cambiando la elección del marco de referencia. Duhem respondió diciendo que la ley produce predicciones cuando se combina con hipótesis auxiliares que fijan el marco de referencia y, por lo tanto, no es diferente de cualquier otra teoría física. [88] Duhem dijo que, aunque las hipótesis individuales pueden no hacer predicciones observables por sí solas, pueden confirmarse como partes de sistemas de hipótesis. Quine extendió esta idea a las hipótesis matemáticas, afirmando que, aunque las hipótesis matemáticas no tienen contenido empírico por sí mismas, pueden participar en las confirmaciones empíricas de los sistemas de hipótesis en los que están contenidas. [89] Esta tesis más tarde llegó a ser conocida como la tesis de Duhem-Quine . [90]
Quine describió su naturalismo como el "abandono del objetivo de una primera filosofía. Ve la ciencia natural como una investigación de la realidad, falible y corregible pero no responsable ante ningún tribunal supracientífico, y no necesitada de ninguna justificación más allá de la observación y el método hipotético-deductivo ". [91] El término "primera filosofía" se utiliza en referencia a las Meditaciones de Descartes sobre la filosofía primera , en las que Descartes utilizó su método de la duda en un intento de asegurar los fundamentos de la ciencia. Quine dijo que los intentos de Descartes de proporcionar los fundamentos de la ciencia habían fracasado y que el proyecto de encontrar una justificación fundamental para la ciencia debía ser rechazado porque creía que la filosofía nunca podría proporcionar un método de justificación más convincente que el método científico. [92]
Quine también fue influenciado por los positivistas lógicos , como su maestro Rudolf Carnap ; su naturalismo fue formulado en respuesta a muchas de sus ideas. [93] Para los positivistas lógicos, todas las creencias justificadas eran reducibles a datos sensoriales , incluido nuestro conocimiento de objetos ordinarios como los árboles. [94] Quine criticó los datos sensoriales como contraproducentes, diciendo que debemos creer en objetos ordinarios para organizar nuestras experiencias del mundo. También dijo que debido a que la ciencia es nuestra mejor teoría de cómo la experiencia sensorial nos da creencias sobre los objetos ordinarios, también deberíamos creer en ella. [95] Mientras que los positivistas lógicos dijeron que las afirmaciones individuales deben estar respaldadas por datos sensoriales, el holismo confirmatorio de Quine significa que la teoría científica está inherentemente ligada a la teoría matemática y, por lo tanto, la evidencia de las teorías científicas puede justificar la creencia en objetos matemáticos a pesar de que no se perciban directamente. [94]
Aunque finalmente se convirtió en platónico debido a su formulación del argumento de la indispensabilidad, [96] Quine simpatizó con el nominalismo desde las primeras etapas de su carrera. [97] En una conferencia de 1946, dijo: "Pondré mis cartas sobre la mesa ahora y confesaré mis prejuicios: me gustaría poder aceptar el nominalismo". [98] Él y Nelson Goodman posteriormente publicaron un artículo conjunto en 1947 titulado "Pasos hacia un nominalismo constructivo" [99] como parte de un proyecto en curso de Quine para "establecer un lenguaje nominalista en el que se pueda expresar toda la ciencia natural". [100] Sin embargo, en una carta a Joseph Henry Woodger el año siguiente, Quine dijo que estaba cada vez más convencido de que "la suposición de entidades abstractas y las suposiciones del mundo externo son suposiciones del mismo tipo". [101] Más tarde publicó en 1948 el artículo "Sobre lo que hay", en el que decía que "la analogía entre el mito de las matemáticas y el mito de la física es... sorprendentemente estrecha", lo que marca un cambio hacia su eventual aceptación de un "platonismo renuente". [102]
A lo largo de la década de 1950, Quine mencionó regularmente el platonismo, el nominalismo y el constructivismo como puntos de vista plausibles, y aún no había llegado a una conclusión definitiva sobre cuál era correcto. [103] No está claro exactamente cuándo Quine aceptó el platonismo; en 1953, se distanció de las afirmaciones del nominalismo en su artículo de 1947 con Goodman, pero en 1956, Goodman todavía describía la "deserción" de Quine del nominalismo como "todavía algo tentativa". [104] Según Lieven Decock, Quine había aceptado la necesidad de entidades matemáticas abstractas con la publicación de su libro de 1960 Palabra y objeto , en el que escribió "una doctrina nominalista exhaustiva es demasiado para estar a la altura". [105] Sin embargo, aunque publicó sugerencias del argumento de la indispensabilidad en varios artículos, nunca le dio una formulación detallada. [106]
Putnam presentó explícitamente el argumento por primera vez en su libro de 1971, Filosofía de la lógica, en el que lo atribuyó a Quine. [107] Afirmó que el argumento era "la cuantificación sobre entidades matemáticas es indispensable para la ciencia, tanto formal como física; por lo tanto, deberíamos aceptar dicha cuantificación; pero esto nos compromete a aceptar la existencia de las entidades matemáticas en cuestión". [108] También escribió que Quine había "enfatizado durante años tanto la indispensabilidad de la cuantificación sobre entidades matemáticas como la deshonestidad intelectual de negar la existencia de lo que uno presupone diariamente". [108] El respaldo de Putnam a la versión de Quine del argumento es discutido. La Enciclopedia de Filosofía de Internet afirma: "En su trabajo temprano, Hilary Putnam aceptó la versión de Quine del argumento de la indispensabilidad". [109] Sin embargo, Liggins y Bueno argumentan que Putnam nunca respaldó el argumento y solo lo presentó como un argumento de Quine. [110] En una conferencia de 1990, Putnam dijo que había compartido las opiniones de Quine sobre el argumento de la indispensabilidad desde 1948, cuando era estudiante en Harvard, pero que desde entonces había llegado a estar en desacuerdo con ellas. [111] Más tarde dijo que difería de Quine en su actitud hacia el argumento al menos desde 1975. [112] Las características del argumento con el que Putnam llegó a estar en desacuerdo incluyen su dependencia de una única teoría regimentada y mejor. [109]
En 1975, Putnam formuló su propio argumento de indispensabilidad basado en el argumento de la inexistencia de milagros en la filosofía de la ciencia, que sostiene que el éxito de la ciencia sólo puede explicarse mediante el realismo científico sin que se lo considere milagroso. Ese año escribió: "Creo que el argumento positivo en favor del realismo [en la ciencia] tiene un análogo en el caso del realismo matemático. También aquí, creo, el realismo es la única filosofía que no convierte el éxito de la ciencia en un milagro". [113] La Enciclopedia de Filosofía de Internet denomina a esta versión del argumento "argumento del éxito de Putnam" y lo presenta de la siguiente forma: [109]
Según la Internet Encyclopedia of Philosophy , la primera y la segunda premisas del argumento se han considerado indiscutibles, por lo que la discusión de este argumento se ha centrado en la tercera premisa. Otras posiciones que han intentado proporcionar una razón para el éxito de las matemáticas incluyen las reformulaciones de la ciencia de Field, que explican la utilidad de las matemáticas como una abreviatura conservadora. [109] Putnam ha criticado las reformulaciones de Field por solo aplicarse a la física clásica y por ser poco probable que puedan extenderse a la física fundamental futura. [116]
Según Ian Hacking , no hubo un "desafío concertado" al argumento de la indispensabilidad durante varias décadas después de que Quine lo planteara por primera vez. [117] Chihara, en su libro de 1973 Ontología y el principio del círculo vicioso , fue uno de los primeros filósofos en intentar reformular las matemáticas en respuesta a los argumentos de Quine. [118] Field siguió con Ciencia sin números en 1980 y dominó la discusión sobre el argumento de la indispensabilidad durante las décadas de 1980 y 1990. [119] Con la introducción de argumentos en contra de la primera premisa del argumento, inicialmente por Maddy en la década de 1990 y continuada por Melia y otros en la década de 2000, el enfoque de Field ha llegado a ser conocido como "nominalismo del camino duro" debido a la dificultad de crear reconstrucciones técnicas de la ciencia que requiere. Los enfoques que atacan la primera premisa, por el contrario, han llegado a ser conocidos como "nominalismo del camino fácil". [120]
A menudo se considera que Colyvan presenta la formulación estándar o "canónica" del argumento dentro de los trabajos filosóficos más recientes. [121] La versión de Colyvan del argumento ha sido influyente en los debates de la filosofía contemporánea de las matemáticas. [122] Se diferencia en aspectos clave de los argumentos presentados por Quine y Putnam. La versión de Quine del argumento se basa en traducir las teorías científicas del lenguaje ordinario a la lógica de primer orden para determinar sus compromisos ontológicos, lo que no es requerido explícitamente por Colyvan. Los argumentos de Putnam eran a favor de la objetividad de las matemáticas, pero no necesariamente a favor de los objetos matemáticos. [123] Putnam se ha distanciado explícitamente de esta versión del argumento, diciendo: "desde mi punto de vista, la descripción de Colyvan de mi(s) argumento(s) está lejos de ser correcta", y ha contrastado su argumento de indispensabilidad con "el ficticio 'argumento de indispensabilidad de Quine-Putnam ' ". [124] Colyvan ha dicho que "la atribución a Quine y Putnam [es] un reconocimiento de deudas intelectuales más que una indicación de que el argumento, tal como se presenta, sería respaldado en cada detalle por Quine o Putnam". [125]
El argumento de la indispensabilidad es ampliamente considerado, aunque no universalmente, como el mejor argumento a favor del platonismo en la filosofía de las matemáticas. [126] Según la Enciclopedia de Filosofía de Stanford , algunos dentro del campo lo ven como el único buen argumento a favor del platonismo. [127] Es uno de los pocos argumentos que han llegado a dominar el debate entre el realismo matemático y el antirrealismo matemático. [128] En la filosofía contemporánea, muchos tipos de nominalismo se definen a sí mismos en oposición al argumento de la indispensabilidad, [129] y generalmente se lo considera como el argumento más importante a superar para las visiones nominalistas como el ficcionalismo. [130]
Los argumentos de Quine y Putnam también han sido influyentes fuera de la filosofía de las matemáticas, inspirando argumentos de indispensabilidad en otras áreas de la filosofía. Por ejemplo, David Lewis , que fue estudiante de Quine, utilizó un argumento de indispensabilidad para defender el realismo modal en su libro de 1986 Sobre la pluralidad de mundos . Según su argumento, la cuantificación sobre mundos posibles es indispensable para nuestras mejores teorías filosóficas, por lo que deberíamos creer en su existencia concreta . [131] Otros argumentos de indispensabilidad en metafísica son defendidos por filósofos como David Armstrong , Graeme Forbes y Alvin Plantinga , quienes han defendido la existencia de estados de cosas debido al papel teórico indispensable que desempeñan en nuestras mejores teorías filosóficas de hacedores de verdad , modalidad y mundos posibles. [132] En el campo de la ética, David Enoch ha ampliado el criterio de compromiso ontológico utilizado en el argumento de indispensabilidad de Quine-Putnam para defender el realismo moral . Según el argumento de Enoch sobre la indispensabilidad deliberativa, la indispensabilidad para la deliberación es tan ontológicamente vinculante como la indispensabilidad para la ciencia, y los hechos morales son indispensables para la deliberación. Por lo tanto, según Enoch, deberíamos creer en los hechos morales. [133]