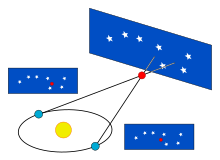
Las medidas de distancia fundamentales más importantes en astronomía provienen de la paralaje trigonométrico , tal como se aplica en el método de paralaje estelar . A medida que la Tierra orbita alrededor del Sol, la posición de las estrellas cercanas parecerá desplazarse ligeramente con respecto al fondo más distante. Estos desplazamientos son ángulos en un triángulo isósceles , con 2 UA (la distancia entre las posiciones extremas de la órbita de la Tierra alrededor del Sol) formando el cateto base del triángulo y la distancia a la estrella siendo los catetos largos de igual longitud. La cantidad de desplazamiento es bastante pequeña, incluso para las estrellas más cercanas, midiendo 1 segundo de arco para un objeto a una distancia de 1 pársec (3,26 años luz ), y luego disminuyendo en cantidad angular a medida que aumenta la distancia. Los astrónomos generalmente expresan las distancias en unidades de pársecs (segundos de arco de paralaje); los años luz se utilizan en los medios populares.
Debido a que la paralaje se hace más pequeña a mayor distancia estelar, las distancias útiles pueden medirse sólo para estrellas que están lo suficientemente cerca como para tener una paralaje mayor que unas pocas veces la precisión de la medición. En la década de 1990, por ejemplo, la misión Hipparcos obtuvo paralajes para más de cien mil estrellas con una precisión de alrededor de un milisegundo de arco , [1] proporcionando distancias útiles para estrellas de hasta unos pocos cientos de parsecs. La Wide Field Camera 3 del telescopio espacial Hubble tiene el potencial de proporcionar una precisión de 20 a 40 microsegundos de arco, lo que permite mediciones de distancias confiables de hasta 5000 parsecs (16 000 años luz) para pequeñas cantidades de estrellas. [2] [3] La misión espacial Gaia proporcionó distancias igualmente precisas para la mayoría de las estrellas más brillantes que la magnitud 15. [4]
Las distancias se pueden medir con un margen de error del 10% hasta el centro galáctico , a unos 30.000 años luz de distancia. Las estrellas tienen una velocidad relativa al Sol que provoca un movimiento propio (transversal a través del cielo) y una velocidad radial (movimiento hacia o desde el Sol). La primera se determina trazando la posición cambiante de las estrellas a lo largo de muchos años, mientras que la segunda proviene de la medición del desplazamiento Doppler del espectro de la estrella causado por el movimiento a lo largo de la línea de visión. Para un grupo de estrellas con la misma clase espectral y un rango de magnitud similar, se puede derivar una paralaje media a partir del análisis estadístico de los movimientos propios en relación con sus velocidades radiales. Este método de paralaje estadístico es útil para medir las distancias de estrellas brillantes más allá de los 50 parsecs y estrellas variables gigantes , incluidas las cefeidas y las variables RR Lyrae . [5]


El movimiento del Sol a través del espacio proporciona una línea base más larga que aumentará la precisión de las mediciones de paralaje, conocida como paralaje secular . Para las estrellas en el disco de la Vía Láctea , esto corresponde a una línea base media de 4 UA por año, mientras que para las estrellas del halo la línea base es de 40 UA por año. Después de varias décadas, la línea base puede ser órdenes de magnitud mayor que la línea base Tierra-Sol utilizada para el paralaje tradicional. Sin embargo, el paralaje secular introduce un mayor nivel de incertidumbre porque la velocidad relativa de las estrellas observadas es una incógnita adicional. Cuando se aplica a muestras de múltiples estrellas, la incertidumbre se puede reducir; la incertidumbre es inversamente proporcional a la raíz cuadrada del tamaño de la muestra. [8]
La paralaje de cúmulos móviles es una técnica que permite utilizar los movimientos de estrellas individuales en un cúmulo estelar cercano para determinar la distancia al cúmulo. Solo los cúmulos abiertos están lo suficientemente cerca como para que esta técnica sea útil. En particular, la distancia obtenida para las Híades ha sido históricamente un paso importante en la escala de distancias.
En circunstancias especiales, se pueden realizar estimaciones de distancias fundamentales para otros objetos individuales. Si se puede observar la expansión de una nube de gas, como un remanente de supernova o una nebulosa planetaria , a lo largo del tiempo, se puede estimar una distancia de paralaje de expansión hasta esa nube. Sin embargo, esas mediciones sufren incertidumbres en la desviación del objeto de la esfericidad. Las estrellas binarias , que son binarias tanto visuales como espectroscópicas, también pueden tener su distancia estimada por medios similares y no sufren la incertidumbre geométrica mencionada anteriormente. La característica común de estos métodos es que se combina una medición del movimiento angular con una medición de la velocidad absoluta (generalmente obtenida a través del efecto Doppler ). La estimación de la distancia proviene del cálculo de qué tan lejos debe estar el objeto para que su velocidad absoluta observada aparezca con el movimiento angular observado.
En particular, las paralajes de expansión pueden proporcionar estimaciones fundamentales de la distancia para objetos que están muy lejos, porque los eyectados de supernova tienen grandes velocidades de expansión y tamaños grandes (en comparación con las estrellas). Además, se pueden observar con interferómetros de radio que pueden medir movimientos angulares muy pequeños. Estos se combinan para proporcionar estimaciones fundamentales de la distancia a las supernovas en otras galaxias. [9] Aunque valiosos, estos casos son bastante raros, por lo que sirven como comprobaciones de consistencia importantes en la escala de distancias en lugar de ser pasos de batalla por sí mismos.

El parsec (símbolo: pc) es una unidad de longitud utilizada para medir las grandes distancias a objetos astronómicos fuera del Sistema Solar , aproximadamente igual a 3,26 años luz o 206.265 unidades astronómicas (UA), es decir, 30,9 billones de kilómetros (19,2 billones de millas ). [a] La unidad parsec se obtiene mediante el uso de paralaje y trigonometría , y se define como la distancia a la que 1 UA subtiende un ángulo de un segundo de arco [10 ] (1/3600 de un grado ). La estrella más cercana, Próxima Centauri , está a unos 1,3 parsecs (4,2 años luz) del Sol : desde esa distancia, la brecha entre la Tierra y el Sol abarca un poco menos de 1/3600 de un grado de visión. [11] La mayoría de las estrellas visibles a simple vista están a unos pocos cientos de parsecs del Sol, las más distantes a unos pocos miles de parsecs y la galaxia de Andrómeda a más de 700.000 parsecs. [12]
La palabra pársec es un acrónimo de "paralaje de un segundo" y fue acuñada por el astrónomo británico Herbert Hall Turner en 1913 [13] para simplificar los cálculos de los astrónomos de distancias astronómicas a partir de datos de observación en bruto. En parte por esta razón, es la unidad preferida en astronomía y astrofísica , aunque el año luz sigue siendo prominente en los textos de divulgación científica y el uso común. Aunque los pársecs se utilizan para las distancias más cortas dentro de la Vía Láctea , se requieren múltiplos de pársecs para las escalas más grandes en el universo, incluidos los kilo pársecs (kpc) para los objetos más distantes dentro y alrededor de la Vía Láctea, los mega pársecs (Mpc) para las galaxias de distancia media y los giga pársecs (Gpc) para muchos cuásares y las galaxias más distantes.
En agosto de 2015, la Unión Astronómica Internacional (UAI) aprobó la Resolución B2 que, como parte de la definición de una escala de magnitud bolométrica absoluta y aparente estandarizada , mencionó una definición explícita existente del pársec como exactamente648 000/π au, o aproximadamente3.085 677 581 491 3673 × 10 16 metros (según la definición de la unidad astronómica de la UAI de 2012). Esto corresponde a la definición de ángulo pequeño del pársec que se encuentra en muchas referencias astronómicas. [14] [15]
En el modelo copernicano, la paralaje estelar creada por el movimiento relativo entre la Tierra y una estrella se puede considerar como resultado de la órbita de la Tierra alrededor del Sol: la estrella solo parece moverse en relación con objetos más distantes en el cielo. En un modelo geoestático, el movimiento de la estrella tendría que considerarse real y oscilar en el cielo con respecto a las estrellas del fondo.
La paralaje estelar se mide con mayor frecuencia utilizando el paralaje anual , definido como la diferencia en la posición de una estrella vista desde la Tierra y el Sol, es decir, el ángulo subtendido en una estrella por el radio medio de la órbita de la Tierra alrededor del Sol. El parsec (3,26 años luz ) se define como la distancia para la cual el paralaje anual es 1 segundo de arco . El paralaje anual normalmente se mide observando la posición de una estrella en diferentes momentos del año a medida que la Tierra se mueve a través de su órbita. La medición del paralaje anual fue la primera forma confiable de determinar las distancias a las estrellas más cercanas. Las primeras mediciones exitosas del paralaje estelar fueron realizadas por Friedrich Bessel en 1838 para la estrella 61 Cygni usando un heliómetro . [16] El paralaje estelar sigue siendo el estándar para calibrar otros métodos de medición. Los cálculos precisos de la distancia basados en el paralaje estelar requieren una medición de la distancia de la Tierra al Sol, ahora basada en la reflexión del radar en las superficies de los planetas. [17]
Los ángulos involucrados en estos cálculos son muy pequeños y por lo tanto difíciles de medir. La estrella más cercana al Sol (y por lo tanto la estrella con la paralaje más grande), Próxima Centauri , tiene un paralaje de 0,7687 ± 0,0003 segundos de arco. [18] Este ángulo es aproximadamente el subtendido por un objeto de 2 centímetros de diámetro ubicado a 5,3 kilómetros de distancia.

El hecho de que la paralaje estelar fuera tan pequeño que no se pudiera observar en aquella época se utilizó como principal argumento científico contra el heliocentrismo durante la temprana edad moderna. De la geometría de Euclides se desprende claramente que el efecto sería indetectable si las estrellas estuvieran lo suficientemente lejos, pero por diversas razones unas distancias tan gigantescas parecían totalmente improbables: una de las principales objeciones de Tycho al heliocentrismo copernicano era que, para que fuera compatible con la falta de paralaje estelar observable, tendría que haber un enorme e improbable vacío entre la órbita de Saturno (en aquel entonces el planeta más distante conocido) y la octava esfera (las estrellas fijas). [20]
En 1989, se lanzó el satélite Hipparcos principalmente para obtener paralajes mejorados y movimientos propios para más de 100.000 estrellas cercanas, aumentando el alcance del método diez veces. Aun así, Hipparcos solo pudo medir ángulos de paralaje para estrellas hasta unos 1.600 años luz de distancia, un poco más del uno por ciento del diámetro de la Vía Láctea . La misión Gaia de la Agencia Espacial Europea , lanzada en diciembre de 2013, puede medir ángulos de paralaje con una precisión de 10 microsegundos de arco , cartografiando así estrellas cercanas (y potencialmente planetas) hasta una distancia de decenas de miles de años luz de la Tierra. [21] [22] En abril de 2014, los astrónomos de la NASA informaron que el telescopio espacial Hubble , mediante el uso del escaneo espacial, puede medir con precisión distancias de hasta 10.000 años luz de distancia, una mejora diez veces mayor que las mediciones anteriores. [19]
La paralaje diurna es una paralaje que varía con la rotación de la Tierra o con una diferencia de ubicación en la Tierra. La Luna y, en menor medida, los planetas terrestres o asteroides vistos desde diferentes posiciones de observación en la Tierra (en un momento dado) pueden aparecer colocados de forma diferente contra el fondo de estrellas fijas. [23] [24]
La paralaje diurna fue utilizada por John Flamsteed en 1672 para medir la distancia a Marte en su oposición y a través de ello estimar la unidad astronómica y el tamaño del Sistema Solar . [25]
La paralaje lunar (a menudo abreviatura de paralaje horizontal lunar o paralaje horizontal ecuatorial lunar ) es un caso especial de paralaje (diurno): la Luna, al ser el cuerpo celeste más cercano, tiene por lejos el paralaje máximo más grande de todos los cuerpos celestes, superando a veces 1 grado. [26]
El diagrama de paralaje estelar también puede ilustrar el paralaje lunar si se reduce la escala del diagrama y se modifica ligeramente. En lugar de "estrella cercana", se lee "Luna" y, en lugar de tomar el círculo en la parte inferior del diagrama para representar el tamaño de la órbita de la Tierra alrededor del Sol, se toma como el tamaño del globo terrestre y un círculo alrededor de la superficie de la Tierra. Entonces, el paralaje lunar (horizontal) equivale a la diferencia en la posición angular, en relación con el fondo de estrellas distantes, de la Luna vista desde dos posiciones de observación diferentes en la Tierra.
Una de las posiciones de observación es el lugar desde el que se puede ver la Luna directamente sobre la cabeza en un momento dado, es decir, vista a lo largo de la línea vertical del diagrama. La otra posición de observación es un lugar desde el que se puede ver la Luna en el horizonte en el mismo momento, es decir, vista a lo largo de una de las líneas diagonales, desde una posición de la superficie de la Tierra que corresponde aproximadamente a uno de los puntos azules del diagrama modificado.
La paralaje lunar (horizontal) se puede definir alternativamente como el ángulo subtendido a la distancia de la Luna por el radio de la Tierra [27] [28] —igual al ángulo p en el diagrama cuando se reduce y modifica como se mencionó anteriormente.
La paralaje horizontal lunar en cualquier momento depende de la distancia lineal de la Luna a la Tierra. La distancia lineal Tierra-Luna varía continuamente a medida que la Luna sigue su órbita perturbada y aproximadamente elíptica alrededor de la Tierra. El rango de variación en la distancia lineal es de aproximadamente 56 a 63,7 radios terrestres, correspondientes a un paralaje horizontal de aproximadamente un grado de arco, pero que varía de aproximadamente 61,4' a aproximadamente 54'. [26] El Almanaque Astronómico y publicaciones similares tabulan el paralaje horizontal lunar y/o la distancia lineal de la Luna a la Tierra de manera periódica, por ejemplo, diariamente para conveniencia de los astrónomos (y de los navegantes celestiales), y el estudio de cómo esta coordenada varía con el tiempo forma parte de la teoría lunar .

El paralaje también se puede utilizar para determinar la distancia a la Luna .
Una forma de determinar la paralaje lunar desde una ubicación es utilizando un eclipse lunar. Una sombra completa de la Tierra sobre la Luna tiene un radio de curvatura aparente igual a la diferencia entre los radios aparentes de la Tierra y el Sol vistos desde la Luna. Se puede ver que este radio es igual a 0,75 grados, de los cuales (con el radio solar aparente de 0,25 grados) obtenemos un radio aparente de la Tierra de 1 grado. Esto da como resultado para la distancia Tierra-Luna 60,27 radios terrestres o 384.399 kilómetros (238.854 mi). Este procedimiento fue utilizado por primera vez por Aristarco de Samos [29] e Hiparco , y más tarde se abrió camino en la obra de Ptolomeo . [30]
El diagrama de la derecha muestra cómo surge la paralaje lunar diario en el modelo planetario geocéntrico y geostático, en el que la Tierra está en el centro del sistema planetario y no gira. También ilustra el importante punto de que el paralaje no tiene por qué ser causado por ningún movimiento del observador, al contrario de algunas definiciones de paralaje que dicen que sí lo es, sino que puede surgir puramente del movimiento del observado.
Otro método consiste en tomar dos fotografías de la Luna al mismo tiempo desde dos lugares de la Tierra y comparar las posiciones de la Luna en relación con las estrellas. Utilizando la orientación de la Tierra, esas dos mediciones de posición y la distancia entre los dos lugares de la Tierra, se puede triangular la distancia a la Luna:

Éste es el método al que se refiere Julio Verne en su novela De la Tierra a la Luna de 1865 :
Hasta entonces, mucha gente no tenía ni idea de cómo se podía calcular la distancia que separaba la Luna de la Tierra. Se aprovechó la circunstancia para enseñarles que esta distancia se obtenía midiendo la paralaje de la Luna. Si la palabra paralaje parecía sorprenderles, se les decía que era el ángulo subtendido por dos líneas rectas que iban desde ambos extremos del radio de la Tierra hasta la Luna. Si tenían dudas sobre la perfección de este método, se les demostraba inmediatamente que no sólo esta distancia media ascendía a un total de doscientas treinta y cuatro mil trescientas cuarenta y siete millas (94.330 leguas), sino que además los astrónomos no se equivocaban en más de setenta millas (≈ 30 leguas).
Después de que Copérnico propusiera su sistema heliocéntrico , con la Tierra en revolución alrededor del Sol, fue posible construir un modelo de todo el Sistema Solar sin escala. Para determinar la escala, sólo es necesario medir una distancia dentro del Sistema Solar, por ejemplo, la distancia media de la Tierra al Sol (ahora llamada unidad astronómica o UA). Cuando se encuentra por triangulación , se denomina paralaje solar , la diferencia en la posición del Sol visto desde el centro de la Tierra y un punto a un radio terrestre de distancia, es decir, el ángulo subtendido en el Sol por el radio medio de la Tierra. Conocer el paralaje solar y el radio medio de la Tierra permite calcular la UA, el primer y pequeño paso en el largo camino de establecer el tamaño y la edad de expansión [31] del Universo visible.
Aristarco de Samos propuso ya en su libro Sobre los tamaños y las distancias del Sol y la Luna una forma primitiva de determinar la distancia al Sol en función de la distancia a la Luna . Observó que el Sol, la Luna y la Tierra forman un triángulo rectángulo (con el ángulo recto en la Luna) en el momento del primer o último cuarto lunar . Luego estimó que el ángulo Luna-Tierra-Sol era de 87°. Utilizando una geometría correcta pero datos de observación inexactos, Aristarco concluyó que el Sol estaba ligeramente menos de 20 veces más lejos que la Luna. El valor real de este ángulo es cercano a 89° 50', y el Sol está unas 390 veces más lejos. [29]
Aristarco señaló que la Luna y el Sol tienen tamaños angulares aparentes casi iguales y, por lo tanto, sus diámetros deben ser proporcionales a sus distancias a la Tierra. Por lo tanto, concluyó que el Sol era aproximadamente 20 veces más grande que la Luna. Esta conclusión, aunque incorrecta, se desprende lógicamente de sus datos incorrectos. Sugiere que el Sol es más grande que la Tierra, lo que podría tomarse como apoyo al modelo heliocéntrico. [32]

Aunque los resultados de Aristarco eran incorrectos debido a errores de observación, se basaban en principios geométricos correctos de paralaje, y se convirtieron en la base para las estimaciones del tamaño del Sistema Solar durante casi 2000 años, hasta que se observó correctamente el tránsito de Venus en 1761 y 1769. [29] Este método fue propuesto por Edmond Halley en 1716, aunque no vivió para ver los resultados. El uso de los tránsitos de Venus tuvo menos éxito del que se esperaba debido al efecto de la gota negra , pero la estimación resultante, 153 millones de kilómetros, es solo un 2% superior al valor actualmente aceptado, 149,6 millones de kilómetros.
Mucho más tarde, el Sistema Solar fue "escalado" utilizando la paralaje de asteroides , algunos de los cuales, como Eros , pasan mucho más cerca de la Tierra que Venus. En una oposición favorable, Eros puede aproximarse a la Tierra a 22 millones de kilómetros. [33] Durante la oposición de 1900-1901, se lanzó un programa mundial para realizar mediciones de paralaje de Eros para determinar la paralaje solar [34] (o distancia al Sol), con los resultados publicados en 1910 por Arthur Hinks de Cambridge [35] y Charles D. Perrine del Observatorio Lick , Universidad de California . [36]
Perrine publicó informes de progreso en 1906 [37] y 1908. [38] Tomó 965 fotografías con el reflector Crossley y seleccionó 525 para la medición. [39] Un programa similar fue llevado a cabo, durante una aproximación más cercana, en 1930-1931 por Harold Spencer Jones . [40] El valor de la Unidad Astronómica (aproximadamente la distancia Tierra-Sol) obtenido por este programa se consideró definitivo hasta 1968, cuando los métodos de radar y de paralaje dinámico comenzaron a producir mediciones más precisas.
También se han utilizado las reflexiones de radar , tanto de Venus (1958) como de asteroides, como Ícaro , para determinar la paralaje solar. Hoy en día, el uso de enlaces de telemetría de naves espaciales ha resuelto este viejo problema. El valor de paralaje solar aceptado actualmente es8.794 143 segundos de arco. [41]
El cúmulo estelar abierto Hyades en Tauro se extiende sobre una parte tan grande del cielo, 20 grados, que los movimientos propios derivados de la astrometría parecen converger con cierta precisión hacia un punto de perspectiva al norte de Orión. La combinación del movimiento propio aparente (angular) observado en segundos de arco con el movimiento de retroceso verdadero (absoluto) también observado, tal como lo atestigua el corrimiento al rojo Doppler de las líneas espectrales estelares, permite estimar la distancia al cúmulo (151 años luz) y sus estrellas miembro de la misma manera que se utiliza la paralaje anual. [42]
La paralaje dinámica también se ha utilizado a veces para determinar la distancia a una supernova cuando se observa que el frente de onda óptico del estallido se propaga a través de las nubes de polvo circundantes a una velocidad angular aparente, mientras que se sabe que su verdadera velocidad de propagación es la velocidad de la luz . [43]
A partir de sistemas de posicionamiento relativistas mejorados, se ha desarrollado la paralaje espacio-temporal que generaliza la noción habitual de paralaje sólo en el espacio. De este modo, los campos de eventos en el espacio-tiempo se pueden deducir directamente sin modelos intermedios de curvatura de la luz por cuerpos masivos, como el utilizado en el formalismo PPN , por ejemplo. [44]
Dos técnicas relacionadas permiten determinar las distancias medias de las estrellas modelando sus movimientos. Ambas se denominan paralajes estadísticos o, individualmente, paralajes seculares y paralajes estadísticos clásicos.
El movimiento del Sol a través del espacio proporciona una línea base más larga que aumentará la precisión de las mediciones de paralaje, conocida como paralaje secular . Para las estrellas en el disco de la Vía Láctea, esto corresponde a una línea base media de 4 UA por año. Para las estrellas del halo, la línea base es de 40 UA por año. Después de varias décadas, la línea base puede ser órdenes de magnitud mayor que la línea base Tierra-Sol utilizada para el paralaje tradicional. El paralaje secular introduce un mayor nivel de incertidumbre, porque la velocidad relativa de otras estrellas es una incógnita adicional. Cuando se aplica a muestras de múltiples estrellas, la incertidumbre se puede reducir; la precisión es inversamente proporcional a la raíz cuadrada del tamaño de la muestra. [8]
Las paralajes y distancias medias de un gran grupo de estrellas se pueden estimar a partir de sus velocidades radiales y movimientos propios . Esto se conoce como paralaje estadístico clásico . Los movimientos de las estrellas se modelan para reproducir estadísticamente la dispersión de velocidad en función de su distancia. [8] [45]
En astronomía, el término "paralaje" ha llegado a significar un método para estimar distancias, no necesariamente utilizando un paralaje verdadero, como por ejemplo:
[
párrafo 14, página 342
] Tomando la unidad de distancia R* como la correspondiente a una paralaje de 1″·0 [… Nota al pie:]
* Es necesario un nombre para esta unidad de distancia. El Sr.
Charlier
ha sugerido
Siriómetro
, pero si se puede pasar por alto la violencia al idioma griego,
se podría adoptar la palabra
Astron . El profesor
Turner
sugiere
Parsec
, que puede tomarse como una forma abreviada de "una distancia correspondiente a una paralaje de un segundo".
Algunos han sugerido que su cálculo del tamaño relativo de la Tierra y el Sol llevó a Aristarco a concluir que tenía más sentido que la Tierra se moviera alrededor del Sol, mucho más grande, que al revés.