Un autómata celular (pl. autómatas celulares , abrev. CA ) es un modelo discreto de computación estudiado en la teoría de los autómatas . Los autómatas celulares también se denominan espacios celulares , autómatas de teselación , estructuras homogéneas , estructuras celulares , estructuras de teselación y matrices iterativas . [2] Los autómatas celulares han encontrado aplicación en diversas áreas, incluida la física , la biología teórica y el modelado de microestructuras .
Un autómata celular consta de una cuadrícula regular de celdas , cada una en uno de un número finito de estados , como encendido y apagado (en contraste con una red de mapas acoplada ). La cuadrícula puede tener cualquier número finito de dimensiones. Para cada celda, se define un conjunto de celdas llamado vecindad en relación con la celda especificada. Se selecciona un estado inicial (tiempo t = 0) asignando un estado para cada celda. Se crea una nueva generación (avanzando t en 1), según alguna regla fija (generalmente, una función matemática) [3] que determina el nuevo estado de cada celda en términos del estado actual de la celda y los estados de las celdas. en su barrio. Normalmente, la regla para actualizar el estado de las celdas es la misma para cada celda y no cambia con el tiempo, y se aplica a toda la cuadrícula simultáneamente, [4] aunque se conocen excepciones, como el autómata celular estocástico y el autómata celular asíncrono. .
El concepto fue descubierto originalmente en la década de 1940 por Stanislaw Ulam y John von Neumann cuando eran contemporáneos en el Laboratorio Nacional de Los Álamos . Si bien algunos lo estudiaron durante las décadas de 1950 y 1960, no fue hasta la década de 1970 y el Juego de la vida de Conway , un autómata celular bidimensional, que el interés en el tema se expandió más allá de la academia. En la década de 1980, Stephen Wolfram emprendió un estudio sistemático de los autómatas celulares unidimensionales, o lo que él llama autómatas celulares elementales ; Su asistente de investigación Matthew Cook demostró que una de estas reglas es Turing-completa .
Las clasificaciones principales de autómatas celulares, tal como las describe Wolfram, están numeradas del uno al cuatro. Son, en orden, autómatas en los que los patrones generalmente se estabilizan hasta alcanzar la homogeneidad , autómatas en los que los patrones evolucionan hacia estructuras mayoritariamente estables u oscilantes, autómatas en los que los patrones evolucionan de una manera aparentemente caótica y autómatas en los que los patrones se vuelven extremadamente complejos y pueden durar por mucho tiempo. mucho tiempo, con estructuras locales estables. Se cree que esta última clase es computacionalmente universal o capaz de simular una máquina de Turing . Los tipos especiales de autómatas celulares son reversibles , donde sólo una única configuración conduce directamente a una posterior, y totalistas , en los que el valor futuro de las células individuales sólo depende del valor total de un grupo de células vecinas. Los autómatas celulares pueden simular una variedad de sistemas del mundo real, incluidos los biológicos y químicos.
Una forma de simular un autómata celular bidimensional es con una hoja infinita de papel cuadriculado junto con un conjunto de reglas a seguir por las células. Cada cuadrado se llama "celda" y cada celda tiene dos estados posibles, blanco y negro. La vecindad de una celda son las celdas cercanas, generalmente adyacentes. Los dos tipos de barrios más comunes son el barrio von Neumann y el barrio Moore . [5] El primero, que lleva el nombre del teórico fundador del autómata celular, consta de cuatro celdas ortogonalmente adyacentes. [5] Este último incluye el barrio de von Neumann así como las cuatro celdas diagonalmente adyacentes. [5] Para dicha celda y su vecindad de Moore, hay 512 (= 2 9 ) patrones posibles. Para cada uno de los 512 patrones posibles, la tabla de reglas indicaría si la celda central será blanca o negra en el siguiente intervalo de tiempo. El Juego de la Vida de Conway es una versión popular de este modelo. Otro tipo de vecindad común es la vecindad extendida de von Neumann , que incluye las dos celdas más cercanas en cada dirección ortogonal, para un total de ocho. [5] La ecuación general para el número total de autómatas posibles es k k s , donde k es el número de estados posibles para una celda y s es el número de celdas vecinas (incluida la celda que se va a calcular) utilizadas para determinar el siguiente estado de la célula. [6] Por lo tanto, en el sistema bidimensional con una vecindad de Moore, el número total de autómatas posibles sería 2 2 9 , o1,34 × 10154 .
Generalmente se supone que todas las células del universo comienzan en el mismo estado, excepto un número finito de células en otros estados; la asignación de valores de estado se llama configuración . [7] De manera más general, a veces se supone que el universo comienza cubierto por un patrón periódico, y que sólo un número finito de células viola ese patrón. Esta última suposición es común en los autómatas celulares unidimensionales.

Los autómatas celulares a menudo se simulan en una cuadrícula finita en lugar de infinita. En dos dimensiones, el universo sería un rectángulo en lugar de un plano infinito. El problema obvio con las cuadrículas finitas es cómo manejar las celdas en los bordes. La forma en que se manejen afectará los valores de todas las celdas de la cuadrícula. Un método posible es permitir que los valores en esas celdas permanezcan constantes. Otro método consiste en definir los barrios de forma diferente para estas células. Se podría decir que tienen menos vecinos, pero también habría que definir nuevas reglas para las celdas ubicadas en los bordes. Estas celdas generalmente se manejan con condiciones de contorno periódicas que dan como resultado una disposición toroidal : cuando uno sale por arriba, entra en la posición correspondiente en la parte inferior, y cuando uno sale por la izquierda, entra por la derecha. (Esto esencialmente simula un mosaico periódico infinito, y en el campo de las ecuaciones diferenciales parciales a veces se lo denomina condiciones de contorno periódicas ). Esto se puede visualizar como pegar con cinta adhesiva los bordes izquierdo y derecho del rectángulo para formar un tubo y luego pegar con cinta adhesiva la parte superior. y los bordes inferiores del tubo para formar un toro (forma de rosquilla). Los universos de otras dimensiones se manejan de manera similar. Esto resuelve problemas de límites con vecindades, pero otra ventaja es que es fácilmente programable utilizando funciones aritméticas modulares . Por ejemplo, en un autómata celular unidimensional como los ejemplos siguientes, la vecindad de una celda x i t es { x i −1 t −1 , x i t −1 , x i +1 t −1 }, donde t es el paso de tiempo (vertical) e i es el índice (horizontal) en una generación.
Stanislaw Ulam , mientras trabajaba en el Laboratorio Nacional de Los Álamos en la década de 1940, estudió el crecimiento de cristales, utilizando una red reticular simple como modelo. [8] Al mismo tiempo, John von Neumann , colega de Ulam en Los Álamos, estaba trabajando en el problema de los sistemas autorreplicantes . [9] El diseño inicial de Von Neumann se basó en la noción de que un robot construyera otro robot. Este diseño se conoce como modelo cinemático. [10] [11] Mientras desarrollaba este diseño, von Neumann se dio cuenta de la gran dificultad de construir un robot autorreplicante y del gran costo que implicaba proporcionar al robot un "mar de piezas" a partir del cual construir su replicante. . Neumann escribió un artículo titulado "La teoría general y lógica de los autómatas" para el Simposio Hixon en 1948. [9] Ulam fue quien sugirió utilizar un sistema discreto para crear un modelo reduccionista de autorreplicación. [12] [13] Nils Aall Barricelli realizó muchas de las primeras exploraciones de estos modelos de vida artificial .

Ulam y von Neumann crearon un método para calcular el movimiento de los líquidos a finales de los años cincuenta. El concepto impulsor del método era considerar un líquido como un grupo de unidades discretas y calcular el movimiento de cada una en función del comportamiento de sus vecinos. [14] Así nació el primer sistema de autómatas celulares. Al igual que la red reticular de Ulam, los autómatas celulares de von Neumann son bidimensionales y su autorreplicador está implementado algorítmicamente. El resultado fue una copiadora y constructora universal que trabajaba dentro de un autómata celular con una vecindad pequeña (sólo las células que se tocan son vecinas; para los autómatas celulares de von Neumann, sólo células ortogonales ), y con 29 estados por célula. [15] Von Neumann dio una prueba de existencia de que un patrón particular haría infinitas copias de sí mismo dentro del universo celular dado al diseñar una configuración de 200.000 células que pudiera hacerlo. [15] Este diseño se conoce como modelo de teselación y se denomina constructor universal de von Neumann . [dieciséis]
También en la década de 1940, Norbert Wiener y Arturo Rosenblueth desarrollaron un modelo de medio excitable con algunas de las características de un autómata celular. [17] Su motivación específica fue la descripción matemática de la conducción de impulsos en los sistemas cardíacos. Sin embargo, su modelo no es un autómata celular porque el medio en el que se propagan las señales es continuo y los frentes de onda son curvos. [17] [18] JM Greenberg y SP Hastings desarrollaron y estudiaron un verdadero modelo de autómata celular de medios excitables en 1978; véase Autómata celular Greenberg-Hastings . El trabajo original de Wiener y Rosenblueth contiene muchas ideas y sigue siendo citado en publicaciones de investigación modernas sobre arritmia cardíaca y sistemas excitables. [19]
En la década de 1960, los autómatas celulares fueron estudiados como un tipo particular de sistema dinámico y se estableció por primera vez la conexión con el campo matemático de la dinámica simbólica . En 1969, Gustav A. Hedlund recopiló muchos resultados siguiendo este punto de vista [20] en lo que todavía se considera un artículo fundamental para el estudio matemático de los autómatas celulares. El resultado más fundamental es la caracterización en el teorema de Curtis-Hedlund-Lyndon del conjunto de reglas globales de los autómatas celulares como el conjunto de endomorfismos continuos de espacios de cambio .
En 1969, el pionero informático alemán Konrad Zuse publicó su libro Calculando el espacio , proponiendo que las leyes físicas del universo son discretas por naturaleza y que el universo entero es el resultado de un cálculo determinista en un único autómata celular; La "teoría de Zuse" se convirtió en la base del campo de estudio llamado física digital . [21]
También en 1969, el científico informático Alvy Ray Smith completó una tesis doctoral en Stanford sobre la teoría de los autómatas celulares, el primer tratamiento matemático de la CA como una clase general de computadoras. Muchos artículos surgieron de esta disertación: mostró la equivalencia de vecindarios de varias formas, cómo reducir un vecindario de Moore a un vecindario de von Neumann o cómo reducir cualquier vecindario a un vecindario de von Neumann. [22] Demostró que las CA bidimensionales son computacionales universales, introdujo las CA unidimensionales y demostró que también son computacionales universales, incluso con vecindades simples. [23] Mostró cómo subsumir la compleja prueba de von Neumann de la universalidad de la construcción (y, por tanto, de las máquinas autorreproductoras) en una consecuencia de la universalidad de la computación en una CA unidimensional. [24] Con la intención de ser la introducción a la edición alemana del libro de von Neumann sobre CA, escribió un estudio del campo con docenas de referencias a artículos de muchos autores en muchos países durante aproximadamente una década de trabajo, a menudo pasados por alto por los modernos. Investigadores de CA. [25]
En la década de 1970, un autómata celular bidimensional y de dos estados llamado Game of Life se hizo ampliamente conocido, particularmente entre la primera comunidad informática. Inventado por John Conway y popularizado por Martin Gardner en un artículo de Scientific American , [26] sus reglas son las siguientes:
A pesar de su simplicidad, el sistema logra una impresionante diversidad de comportamiento, fluctuando entre la aparente aleatoriedad y el orden. Una de las características más evidentes del Juego de la Vida es la frecuente aparición de planeadores , disposiciones de células que esencialmente se mueven solas a través de la cuadrícula. Es posible disponer el autómata para que los planeadores interactúen para realizar cálculos, y después de mucho esfuerzo se ha demostrado que el Juego de la Vida puede emular una máquina universal de Turing . [27] Fue visto como un tema en gran medida recreativo, y se realizó poco trabajo de seguimiento aparte de investigar las particularidades del Juego de la Vida y algunas reglas relacionadas a principios de la década de 1970. [28]
Stephen Wolfram comenzó a trabajar de forma independiente en autómatas celulares a mediados de 1981, después de considerar cómo patrones complejos parecían formarse en la naturaleza en violación de la Segunda Ley de la Termodinámica . [29] Sus investigaciones fueron impulsadas inicialmente por el deseo de modelar sistemas como las redes neuronales que se encuentran en el cerebro. [29] Publicó su primer artículo en Reviews of Modern Physics investigando autómatas celulares elementales ( Regla 30 en particular) en junio de 1983. [2] [29] La inesperada complejidad del comportamiento de estas reglas simples llevó a Wolfram a sospechar que la complejidad en La naturaleza puede deberse a mecanismos similares. [29] Sus investigaciones, sin embargo, lo llevaron a darse cuenta de que los autómatas celulares eran pobres en el modelado de redes neuronales. [29] Además, durante este período Wolfram formuló los conceptos de aleatoriedad intrínseca e irreductibilidad computacional , [30] y sugirió que la regla 110 puede ser universal , un hecho demostrado más tarde por el asistente de investigación de Wolfram, Matthew Cook, en la década de 1990. [31]
Wolfram, en A New Kind of Science y varios artículos que datan de mediados de la década de 1980, definió cuatro clases en las que se pueden dividir los autómatas celulares y varios otros modelos computacionales simples dependiendo de su comportamiento. Mientras que estudios anteriores en autómatas celulares tendían a intentar identificar tipos de patrones para reglas específicas, la clasificación de Wolfram fue el primer intento de clasificar las reglas mismas. En orden de complejidad las clases son:
Estas definiciones son de naturaleza cualitativa y hay cierto margen de interpretación. Según Wolfram, "... con casi cualquier esquema de clasificación general hay inevitablemente casos que son asignados a una clase por una definición y a otra clase por otra definición. Y lo mismo ocurre con los autómatas celulares: ocasionalmente hay reglas... que mostrar algunas características de una clase y algunas de otra." [34] La clasificación de Wolfram se ha comparado empíricamente con una agrupación de las longitudes comprimidas de las salidas de los autómatas celulares. [35]
Ha habido varios intentos de clasificar los autómatas celulares en clases formalmente rigurosas, inspirados en la clasificación de Wolfram. Por ejemplo, Culik y Yu propusieron tres clases bien definidas (y una cuarta para los autómatas que no coinciden con ninguna de ellas), que a veces se denominan clases Culik-Yu; la membresía en estos resultó indecidible . [36] [37] [38] La clase 2 de Wolfram se puede dividir en dos subgrupos de reglas estables (de punto fijo) y oscilantes (periódicas). [39]
La idea de que hay 4 clases de sistemas dinámicos surgió originalmente del químico ganador del Premio Nobel Ilya Prigogine , quien identificó estas 4 clases de sistemas termodinámicos: (1) sistemas en equilibrio termodinámico, (2) sistemas espacial/temporalmente uniformes, (3) caóticos. sistemas, y (4) sistemas complejos lejos del equilibrio con estructuras disipativas (ver figura 1 en el artículo de 1974 de Nicolis, alumno de Prigogine). [40]
Un autómata celular es reversible si, para cada configuración actual del autómata celular, hay exactamente una configuración pasada ( preimagen ). [41] Si uno piensa en un autómata celular como una función que asigna configuraciones a configuraciones, la reversibilidad implica que esta función es biyectiva . [41] Si un autómata celular es reversible, su comportamiento invertido en el tiempo también puede describirse como un autómata celular; este hecho es consecuencia del teorema de Curtis-Hedlund-Lyndon , una caracterización topológica de los autómatas celulares. [42] [43] Para los autómatas celulares en los que no todas las configuraciones tienen una preimagen, las configuraciones sin preimágenes se denominan patrones del Jardín del Edén . [44]
Para los autómatas celulares unidimensionales existen algoritmos conocidos para decidir si una regla es reversible o irreversible. [45] [46] Sin embargo, para autómatas celulares de dos o más dimensiones la reversibilidad es indecidible ; es decir, no existe ningún algoritmo que tome como entrada una regla del autómata y garantice que determinará correctamente si el autómata es reversible. La prueba de Jarkko Kari está relacionada con el problema del mosaico de Wang Tiles . [47]
Los autómatas celulares reversibles se utilizan a menudo para simular fenómenos físicos como la dinámica de gases y fluidos, ya que obedecen las leyes de la termodinámica . Estos autómatas celulares tienen reglas especialmente construidas para ser reversibles. Estos sistemas han sido estudiados por Tommaso Toffoli , Norman Margolus y otros. Se pueden utilizar varias técnicas para construir explícitamente autómatas celulares reversibles con inversas conocidas. Dos comunes son el autómata celular de segundo orden y el autómata celular de bloque , los cuales implican modificar la definición de autómata celular de alguna manera. Aunque dichos autómatas no satisfacen estrictamente la definición dada anteriormente, se puede demostrar que pueden ser emulados por autómatas celulares convencionales con vecindades y números de estados suficientemente grandes y, por lo tanto, pueden considerarse un subconjunto de autómatas celulares convencionales. Por el contrario, se ha demostrado que todo autómata celular reversible puede ser emulado por un autómata celular de bloque. [48] [49]
Una clase especial de autómatas celulares son los autómatas celulares totalistas . El estado de cada celda en un autómata celular totalista está representado por un número (generalmente un valor entero extraído de un conjunto finito), y el valor de una celda en el tiempo t depende sólo de la suma de los valores de las celdas en su vecindad. (posiblemente incluyendo la propia celda) en el momento t − 1. [50] [51] Si el estado de la celda en el momento t depende tanto de su propio estado como del total de sus vecinos en el momento t − 1, entonces el autómata celular es propiamente dicho totalista exterior . [51] El juego de la vida de Conway es un ejemplo de un autómata celular totalista externo con valores de celda 0 y 1; Los autómatas celulares totalistas externos con la misma estructura de vecindad de Moore que la Vida a veces se denominan autómatas celulares realistas . [52] [53]
Hay muchas generalizaciones posibles del concepto de autómata celular.
Una forma es utilizar algo que no sea una cuadrícula rectangular (cúbica, etc. ). Por ejemplo, si un plano está mosaico con hexágonos regulares , esos hexágonos podrían usarse como celdas. En muchos casos, los autómatas celulares resultantes son equivalentes a aquellos con cuadrículas rectangulares con reglas y vecindarios especialmente diseñados. Otra variación sería hacer que la cuadrícula sea irregular, como con los mosaicos de Penrose . [54]
Además, las reglas pueden ser probabilísticas más que deterministas. Estos autómatas celulares se denominan autómatas celulares probabilísticos . Una regla probabilística proporciona, para cada patrón en el momento t , las probabilidades de que la celda central pase a cada estado posible en el momento t + 1. A veces se utiliza una regla más simple; por ejemplo: "La regla es el Juego de la vida, pero en cada paso de tiempo hay una probabilidad del 0,001% de que cada celda pase al color opuesto".
El vecindario o las reglas podrían cambiar con el tiempo o el espacio. Por ejemplo, inicialmente el nuevo estado de una celda podría ser determinado por las celdas adyacentes horizontalmente, pero para la siguiente generación se usarían las celdas verticales.
En los autómatas celulares, el nuevo estado de una célula no se ve afectado por el nuevo estado de otras células. Esto podría cambiarse para que, por ejemplo, un bloque de celdas de 2 por 2 pueda determinarse por sí mismo y las celdas adyacentes a él.
Hay autómatas continuos . Estos son como autómatas celulares totalistas, pero en lugar de que la regla y los estados sean discretos ( por ejemplo, una tabla, usando estados {0,1,2}), se usan funciones continuas y los estados se vuelven continuos (generalmente valores en [0,1 ] ). El estado de una ubicación es un número finito de números reales. Ciertos autómatas celulares pueden producir difusión en patrones líquidos de esta manera.
Los autómatas espaciales continuos tienen un continuo de ubicaciones. El estado de una ubicación es un número finito de números reales. El tiempo también es continuo y el estado evoluciona según ecuaciones diferenciales. Un ejemplo importante son las texturas de reacción-difusión , ecuaciones diferenciales propuestas por Alan Turing para explicar cómo las reacciones químicas podrían crear rayas en las cebras y manchas en los leopardos. [55] Cuando estos se aproximan mediante autómatas celulares, a menudo producen patrones similares. MacLennan [1] considera los autómatas espaciales continuos como modelo de computación.
Se conocen ejemplos de autómatas espaciales continuos, que exhiben fenómenos de propagación análogos a los planeadores en el Juego de la Vida. [56]
Los autómatas de reescritura de gráficos son extensiones de los autómatas celulares basados en sistemas de reescritura de gráficos . [57]
El autómata celular no trivial más simple sería unidimensional, con dos estados posibles por celda y los vecinos de una celda definidos como las celdas adyacentes a cada lado de ella. Una celda y sus dos vecinas forman una vecindad de 3 celdas, por lo que hay 2 3 = 8 patrones posibles para una vecindad. Una regla consiste en decidir, para cada patrón, si la celda será un 1 o un 0 en la siguiente generación. Entonces hay 2 8 = 256 reglas posibles. [6]
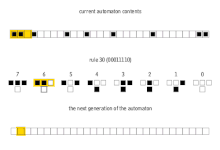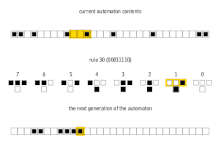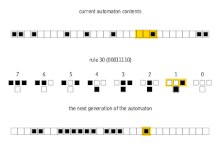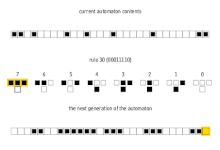
Generalmente se hace referencia a estos 256 autómatas celulares por su código Wolfram , una convención de nomenclatura estándar inventada por Wolfram que le da a cada regla un número del 0 al 255. Varios artículos han analizado y comparado estos 256 autómatas celulares. Son particularmente interesantes los autómatas celulares de la regla 30 , la regla 90 , la regla 110 y la regla 184 . Las imágenes a continuación muestran el historial de las reglas 30 y 110 cuando la configuración inicial consiste en un 1 (en la parte superior de cada imagen) rodeado por 0. Cada fila de píxeles representa una generación en la historia del autómata, siendo t =0 la fila superior. Cada píxel es de color blanco para 0 y negro para 1.

La regla 30 exhibe un comportamiento de clase 3 , lo que significa que incluso patrones de entrada simples como el mostrado conducen a historias caóticas y aparentemente aleatorias.

La regla 110, al igual que el Juego de la Vida, exhibe lo que Wolfram llama comportamiento de clase 4 , que no es completamente aleatorio ni completamente repetitivo. Las estructuras localizadas aparecen e interactúan de diversas formas de apariencia complicada. Durante el desarrollo de Un nuevo tipo de ciencia , como asistente de investigación de Wolfram en 1994, Matthew Cook demostró que algunas de estas estructuras eran lo suficientemente ricas como para sustentar la universalidad . Este resultado es interesante porque la regla 110 es un sistema unidimensional extremadamente simple y difícil de diseñar para que realice un comportamiento específico. Por lo tanto, este resultado proporciona un apoyo significativo a la opinión de Wolfram de que los sistemas de clase 4 tienen una probabilidad inherente de ser universales. Cook presentó su prueba en una conferencia del Instituto Santa Fe sobre Autómatas Celulares en 1998, pero Wolfram bloqueó la inclusión de la prueba en las actas de la conferencia, ya que Wolfram no quería que la prueba se anunciara antes de la publicación de Un nuevo tipo de ciencia . [58] En 2004, la prueba de Cook finalmente se publicó en la revista Complex Systems de Wolfram (Vol. 15, No. 1), más de diez años después de que a Cook se le ocurriera. La regla 110 ha sido la base de algunas de las máquinas universales de Turing más pequeñas. [59]
Una regla de autómata celular elemental está especificada por 8 bits, y se puede considerar que todas las reglas de autómata celular elemental se ubican en los vértices del hipercubo unitario de 8 dimensiones . Este hipercubo unitario es el espacio de reglas del autómata celular. Para los autómatas celulares vecinos más cercanos, una regla se especifica mediante 2 5 = 32 bits, y el espacio de reglas del autómata celular es un hipercubo unitario de 32 dimensiones. La distancia entre dos reglas se puede definir por el número de pasos necesarios para moverse desde un vértice, que representa la primera regla, y otro vértice, que representa otra regla, a lo largo del borde del hipercubo. Esta distancia de regla a regla también se llama distancia de Hamming .
El espacio de reglas de autómatas celulares nos permite preguntarnos si las reglas con comportamiento dinámico similar están "cercanas" entre sí. Dibujar gráficamente un hipercubo de alta dimensión en el plano bidimensional sigue siendo una tarea difícil, y un sencillo localizador de una regla en el hipercubo es el número de bit-1 en la cadena de 8 bits para reglas elementales (o cadena de 32 bits para reglas elementales). las reglas del vecino más cercano). Dibujar las reglas en diferentes clases de Wolfram en estas porciones del espacio de reglas muestra que las reglas de clase 1 tienden a tener un menor número de bits 1, por lo que se ubican en una región del espacio, mientras que las reglas de clase 3 tienden a tener una proporción más alta (50% ) de bits-1. [39]
Para un espacio de reglas de autómata celular más grande, se muestra que las reglas de clase 4 están ubicadas entre las reglas de clase 1 y clase 3. [60] Esta observación es la base de la frase borde del caos , y recuerda la transición de fase en termodinámica .

Varios procesos biológicos ocurren (o pueden ser simulados) mediante autómatas celulares.
Algunos ejemplos de fenómenos biológicos modelados por autómatas celulares con un espacio de estados simple son:
Además, los fenómenos biológicos que requieren un modelado explícito de las velocidades de los agentes (por ejemplo, los involucrados en la migración celular colectiva ) pueden modelarse mediante autómatas celulares con un espacio de estados y reglas más complejos, como los autómatas celulares de gas de red biológica . Estos incluyen fenómenos de gran importancia médica, tales como:
La reacción de Belousov-Zhabotinsky es un oscilador químico espacio-temporal que puede simularse mediante un autómata celular. En la década de 1950 , AM Zhabotinsky (ampliando el trabajo de BP Belousov ) descubrió que cuando se mezclaban una capa delgada y homogénea de una mezcla de ácido malónico , bromato acidificado y una sal cérica y se dejaban sin alterar, se obtenían patrones geométricos fascinantes como círculos concéntricos y Las espirales se propagan a través del medio. En la sección "Recreaciones por computadora" de la edición de agosto de 1988 de Scientific American , [69] AK Dewdney analizó un autómata celular [70] desarrollado por Martin Gerhardt y Heike Schuster de la Universidad de Bielefeld (Alemania). Este autómata produce patrones de ondas que se parecen a los de la reacción de Belousov-Zhabotinsky.

Los autómatas celulares probabilísticos se utilizan en física estadística y de la materia condensada para estudiar fenómenos como la dinámica de fluidos y las transiciones de fase. El modelo de Ising es un ejemplo prototípico, en el que cada celda puede estar en cualquiera de dos estados llamados "arriba" y "abajo", generando una representación idealizada de un imán . Al ajustar los parámetros del modelo, se puede variar la proporción de células que se encuentran en el mismo estado, de manera que ayuden a explicar cómo los ferromagnetos se desmagnetizan cuando se calientan. Además, los resultados del estudio de la transición de fase de desmagnetización se pueden transferir a otras transiciones de fase, como la evaporación de un líquido a gas; esta conveniente aplicabilidad cruzada se conoce como universalidad . [71] [72] La transición de fase en el modelo bidimensional de Ising y otros sistemas en su clase de universalidad ha sido de particular interés, ya que requiere la teoría de campos conforme para comprenderla en profundidad. [73] Otros autómatas celulares que han sido de importancia en la física incluyen los autómatas de red de gas , que simulan flujos de fluidos.
Los procesadores de autómatas celulares son implementaciones físicas de conceptos de CA, que pueden procesar información computacionalmente. Los elementos de procesamiento están dispuestos en una cuadrícula regular de celdas idénticas. La cuadrícula suele ser un mosaico cuadrado, o teselado , de dos o tres dimensiones; otros mosaicos son posibles, pero aún no se utilizan. Los estados de las células están determinados únicamente por las interacciones con las células vecinas adyacentes. No existe ningún medio para comunicarse directamente con células más alejadas. [74] Una de esas configuraciones de matriz de procesador de autómata celular es la matriz sistólica . La interacción celular puede realizarse mediante carga eléctrica, magnetismo, vibración ( fonones a escalas cuánticas) o cualquier otro medio físicamente útil. Esto se puede hacer de varias maneras para que no se necesiten cables entre ningún elemento. Esto es muy diferente a los procesadores utilizados en la mayoría de las computadoras hoy en día ( diseños de von Neumann ) que están divididos en secciones con elementos que pueden comunicarse con elementos distantes a través de cables.
La regla 30 se sugirió originalmente como un posible cifrado de bloques para su uso en criptografía . Se pueden utilizar autómatas celulares bidimensionales para construir un generador de números pseudoaleatorios . [75]
Se han propuesto autómatas celulares para la criptografía de clave pública . La función unidireccional es la evolución de una CA finita cuya inversa se cree que es difícil de encontrar. Dada la regla, cualquiera puede calcular fácilmente los estados futuros, pero parece muy difícil calcular los estados anteriores. Los autómatas celulares también se han aplicado para diseñar códigos de corrección de errores . [76]
Otros problemas que se pueden solucionar con los autómatas celulares incluyen:
Los autómatas celulares se han utilizado en música generativa [77] y composición de música evolutiva [78] y generación de terreno procedimental en videojuegos. [79]
Se pueden utilizar ciertos tipos de autómatas celulares para generar laberintos. [80] Dos autómatas celulares muy conocidos, Maze y Mazectric, tienen cadenas de reglas B3/S12345 y B3/S1234. [80] En el primero, esto significa que las células sobreviven de una generación a la siguiente si tienen al menos uno y como máximo cinco vecinos . En este último caso, esto significa que las células sobreviven si tienen de uno a cuatro vecinos. Si una célula tiene exactamente tres vecinos, nace. Es similar al Juego de la vida de Conway en que los patrones que no tienen una célula viva adyacente a 1, 4 o 5 otras células vivas en cualquier generación se comportarán de manera idéntica. [80] Sin embargo, para patrones grandes, se comporta de manera muy diferente a la Vida. [80]
Para un patrón de inicio aleatorio, estos autómatas celulares generadores de laberintos evolucionarán hacia laberintos complejos con paredes bien definidas que delinean corredores. Mazecetric, que tiene la regla B3/S1234, tiene tendencia a generar pasillos más largos y rectos en comparación con Maze, con la regla B3/S12345. [80] Dado que estas reglas de autómatas celulares son deterministas , cada laberinto generado está determinado únicamente por su patrón de inicio aleatorio. Este es un inconveniente importante ya que los laberintos tienden a ser relativamente predecibles.
Al igual que algunos de los métodos basados en la teoría de grafos descritos anteriormente, estos autómatas celulares suelen generar laberintos a partir de un único patrón inicial; por lo tanto, normalmente será relativamente fácil encontrar el camino a la celda inicial, pero más difícil encontrar el camino a cualquier otro lugar.Las reglas específicas de los autómatas celulares incluyen:
{{cite web}}: Mantenimiento CS1: copia archivada como título ( enlace )