En matemáticas y teoría de la computabilidad , un autómata celular elemental es un autómata celular unidimensional donde hay dos estados posibles (etiquetados 0 y 1) y la regla para determinar el estado de una célula en la siguiente generación depende sólo del estado actual de la celda y sus dos vecinos inmediatos. Existe un autómata celular elemental ( regla 110 , definida a continuación) que es capaz de realizar cálculos universales y, como tal, es uno de los modelos de cálculo más simples posibles.
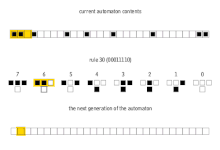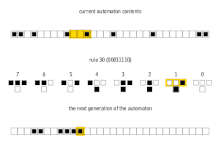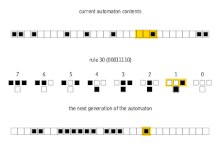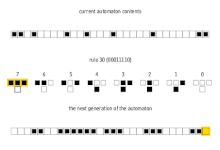
Hay 8 = 2 3 configuraciones posibles para una celda y sus dos vecinos inmediatos. La regla que define el autómata celular debe especificar el estado resultante para cada una de estas posibilidades de modo que haya 256 = 2 2 3 autómatas celulares elementales posibles. Stephen Wolfram propuso un esquema, conocido como código Wolfram , para asignar a cada regla un número del 0 al 255 que se ha convertido en estándar. Cada posible configuración actual se escribe en orden, 111, 110,..., 001, 000, y el estado resultante para cada una de estas configuraciones se escribe en el mismo orden y se interpreta como la representación binaria de un número entero. Este número se considera el número de regla del autómata. Por ejemplo, 110 d = 01101110 2 . Entonces la regla 110 está definida por la regla de transición:
Aunque hay 256 reglas posibles, muchas de ellas son trivialmente equivalentes entre sí hasta una simple transformación de la geometría subyacente. La primera de estas transformaciones es la reflexión a través de un eje vertical y el resultado de aplicar esta transformación a una regla dada se llama regla reflejada . Estas reglas exhibirán el mismo comportamiento hasta la reflexión a través de un eje vertical y, por lo tanto, son equivalentes en un sentido computacional.
Por ejemplo, si se refleja la definición de la regla 110 a través de una línea vertical, se obtiene la siguiente regla (regla 124):
Las reglas que son iguales a su regla reflejada se llaman anfiquirales . De los 256 autómatas celulares elementales, 64 son anfiquirales.
La segunda transformación de este tipo consiste en intercambiar los roles de 0 y 1 en la definición. El resultado de aplicar esta transformación a una regla determinada se llama regla complementaria . Por ejemplo, si se aplica esta transformación a la regla 110, obtenemos la siguiente regla
y, tras reordenar, descubrimos que esta es la regla 137:
Hay 16 reglas que son iguales a sus reglas complementarias.
Finalmente, las dos transformaciones anteriores se pueden aplicar sucesivamente a una regla para obtener la regla complementaria reflejada. Por ejemplo, la regla complementaria reflejada de la regla 110 es la regla 193. Hay 16 reglas que son iguales a sus reglas complementarias reflejadas.
De los 256 autómatas celulares elementales, hay 88 que no son equivalentes bajo estas transformaciones.
Resulta que la reflexión y la complementación son automorfismos del monoide de autómatas celulares unidimensionales, ya que ambos conservan la composición. [1]
Un método utilizado para estudiar estos autómatas es seguir su historial con un estado inicial de todos los ceros excepto una sola celda con un 1. Cuando el número de regla es par (de modo que una entrada de 000 no se calcula como un 1), se convierte en Tiene sentido interpretar el estado en cada momento, t , como un número entero expresado en binario, produciendo una secuencia a ( t ) de números enteros. En muchos casos, estas secuencias tienen expresiones de forma simple y cerrada o tienen una función generadora con una forma simple. Se destacan las siguientes reglas:
La secuencia generada es 1, 3, 5, 11, 21, 43, 85, 171,... (secuencia A001045 en el OEIS ). Esta es la secuencia de números de Jacobsthal y tiene función generadora.
Tiene la expresión de forma cerrada.
La regla 156 genera la misma secuencia.
La secuencia generada es 1, 5, 21, 85, 341, 1365, 5461, 21845,... (secuencia A002450 en el OEIS ). Esto tiene función generadora.
Tiene la expresión de forma cerrada.
Tenga en cuenta que las reglas 58, 114, 122, 178, 186, 242 y 250 generan la misma secuencia.
La secuencia generada es 1, 7, 17, 119, 273, 1911, 4369, 30583,... (secuencia A118108 en el OEIS ). Esto tiene función generadora.
Tiene la expresión de forma cerrada.
La secuencia generada es 1, 3, 5, 15, 17, 51, 85, 255, ... (secuencia A001317 en el OEIS ). Esto se puede obtener tomando filas sucesivas del triángulo de Pascal módulo 2 e interpretándolas como números enteros en binario, que se pueden representar gráficamente mediante un triángulo de Sierpinski .
La secuencia generada es 1, 5, 17, 85, 257, 1285, 4369, 21845,... (secuencia A038183 en el OEIS ). Esto se puede obtener tomando filas sucesivas del triángulo de Pascal módulo 2 e interpretándolas como números enteros en base 4. Tenga en cuenta que las reglas 18, 26, 82, 146, 154, 210 y 218 generan la misma secuencia.
La secuencia generada es 1, 7, 27, 119, 427, 1879, 6827, 30039,... (secuencia A118101 en el OEIS ). Esto se puede expresar como
Esto tiene función generadora.
La secuencia generada es 1, 6, 20, 120, 272, 1632, 5440, 32640,... (secuencia A117998 en el OEIS ). Esta es simplemente la secuencia generada por la regla 60 (que es su regla espejo) multiplicada por potencias sucesivas de 2.
La secuencia generada es 1, 6, 28, 104, 496, 1568, 7360, 27520, 130304, 396800,... (secuencia A117999 en el OEIS ). La regla 110 tiene la quizás sorprendente propiedad de que es Turing completa y, por tanto, capaz de realizar cálculos universales . [2]
La secuencia generada es 1, 7, 21, 107, 273, 1911, 5189, 28123,... (secuencia A038184 en el OEIS ). Esto se puede obtener tomando los coeficientes de las potencias sucesivas de (1+ x + x 2 ) módulo 2 e interpretándolos como números enteros en binario.
La secuencia generada es 1, 7, 29, 115, 477, 1843, 7645, 29491,... (secuencia A118171 en el OEIS ). Esto tiene función generadora.
La secuencia generada es 1, 3, 5, 15, 29, 55, 93, 247,... (secuencia A118173 en el OEIS ). Esto tiene función generadora.
La secuencia generada es 1, 7, 29, 119, 477, 1911, 7645, 30583,... (secuencia A037576 en el OEIS ). Esto tiene función generadora.
La secuencia generada es 1, 3, 7, 15, 31, 63, 127, 255,... (secuencia A000225 en el OEIS ). Esta es la secuencia de números de Mersenne y tiene función generadora.
Tiene la expresión de forma cerrada.
Nota: la regla 252 genera la misma secuencia.
La secuencia generada es 1, 7, 31, 127, 511, 2047, 8191, 32767,... (secuencia A083420 en el OEIS ). Esta es cualquier otra entrada en la secuencia de números de Mersenne y tiene una función generadora.
Tiene la expresión de forma cerrada.
Tenga en cuenta que la regla 254 genera la misma secuencia.
Estas imágenes representan diagramas espacio-temporales, en los que cada fila de píxeles muestra las celdas del autómata en un único punto en el tiempo, y el tiempo aumenta hacia abajo. Comienzan con un estado de autómata inicial en el que una sola celda, el píxel en el centro de la fila superior de píxeles, está en el estado 1 y todas las demás celdas están en 0.
Una segunda forma de investigar el comportamiento de estos autómatas es examinar su historia comenzando con un estado aleatorio. Este comportamiento se puede entender mejor en términos de clases de Wolfram. Wolfram da los siguientes ejemplos como reglas típicas de cada clase. [3]
Cada resultado calculado se coloca debajo de la fuente de ese resultado creando una representación bidimensional de la evolución del sistema.
En la siguiente galería, se muestra esta evolución a partir de condiciones iniciales aleatorias para cada una de las 88 reglas no equivalentes. Debajo de cada imagen está el número de regla utilizado para producir la imagen, y entre paréntesis se incluyen los números de reglas equivalentes producidas por reflexión o complementación, si existen. [5] Como se mencionó anteriormente, la regla reflejada produciría una imagen reflejada, mientras que la regla complementaria produciría una imagen con blanco y negro intercambiados.
En algunos casos, el comportamiento de un autómata celular no es inmediatamente evidente. Por ejemplo, para la Regla 62, las estructuras que interactúan se desarrollan como en una Clase 4. Pero en estas interacciones al menos una de las estructuras es aniquilada por lo que el autómata eventualmente entra en un estado repetitivo y el autómata celular es Clase 2. [6]
La regla 73 es Clase 2 [7] porque cada vez que hay dos unos consecutivos rodeados por ceros, esta característica se conserva en las generaciones siguientes. Esto crea efectivamente muros que bloquean el flujo de información entre diferentes partes de la matriz. Hay un número finito de configuraciones posibles en la sección entre dos paredes, por lo que el autómata eventualmente debe comenzar a repetir dentro de cada sección, aunque el período puede ser muy largo si la sección es lo suficientemente ancha. Estos muros se formarán con probabilidad 1 para condiciones iniciales completamente aleatorias. Sin embargo, si se agrega la condición de que las longitudes de las corridas de 0 o 1 consecutivos siempre deben ser impares, entonces el autómata muestra un comportamiento de Clase 3 ya que las paredes nunca se pueden formar.
La regla 54 es Clase 4 [8] y también parece ser capaz de realizar cálculos universales, pero no se ha estudiado tan a fondo como la Regla 110. Se han catalogado muchas estructuras interactivas que en conjunto se espera que sean suficientes para la universalidad. [9]
![{\displaystyle a(t)={\begin{casos}1,&{\mbox{if }}t=0\\[5px]7,&{\mbox{if }}t=1\\[7px] {\dfrac {1+5\cdot 4^{n}}{3}},&{\mbox{si }}t{\mbox{ es incluso en caso contrario}}\\[7px]{\dfrac {10+11 \cdot 4^{n}}{6}},&{\mbox{si }}t{\mbox{ es impar en caso contrario}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c00935a30e164dd3284bedaae140a667de008a6)
