La curva de Phillips es un modelo económico , llamado así en honor a Bill Phillips , que relaciona la reducción del desempleo con el aumento de los salarios en una economía. [1] Si bien Phillips no vinculó directamente el empleo con la inflación , esta fue una deducción trivial de sus hallazgos estadísticos. Paul Samuelson y Robert Solow hicieron explícita la conexión y, posteriormente, Milton Friedman [2] y Edmund Phelps [3] [4] pusieron en marcha la estructura teórica.
Si bien existe una disyuntiva a corto plazo entre desempleo e inflación, no se ha observado en el largo plazo. [5] En 1967 y 1968, Friedman y Phelps afirmaron que la curva de Phillips sólo era aplicable en el corto plazo y que, en el largo plazo, las políticas inflacionarias no reducirían el desempleo. [2] [3] [4] [6] Friedman predijo correctamente la estanflación de la década de 1970. [7]
En la década de 2010 [8], la pendiente de la curva de Phillips parece haber disminuido y ha habido controversia sobre su utilidad para predecir la inflación. Un estudio de 2022 concluyó que la pendiente de la curva de Phillips es pequeña y lo era incluso a principios de la década de 1980. [9] No obstante, los bancos centrales todavía utilizan la curva de Phillips para comprender y pronosticar la inflación. [10]
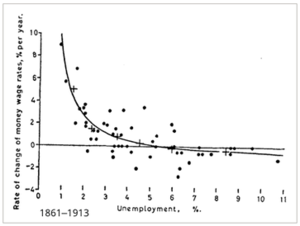
Bill Phillips , un economista nacido en Nueva Zelanda , escribió un artículo en 1958 titulado "La relación entre el desempleo y la tasa de cambio de los salarios monetarios en el Reino Unido, 1861-1957", que se publicó en la revista trimestral Economica . [11] En el artículo, Phillips describe cómo observó una relación inversa entre los cambios en los salarios monetarios y el desempleo en la economía británica durante el período examinado. Se encontraron patrones similares en otros países y en 1960 Paul Samuelson y Robert Solow tomaron el trabajo de Phillips e hicieron explícito el vínculo entre la inflación y el desempleo: cuando la inflación era alta, el desempleo era bajo, y viceversa. [12]
En la década de 1920, el economista estadounidense Irving Fisher había observado esta relación entre el desempleo y los precios. Sin embargo, la curva original de Phillips describía el comportamiento de los salarios monetarios. [13]
En los años posteriores al artículo de Phillips de 1958, muchos economistas de los países industriales avanzados creyeron que sus resultados mostraban una relación permanentemente estable entre la inflación y el desempleo. [ cita requerida ] Una implicación de esto fue que los gobiernos podían controlar el desempleo y la inflación con una política keynesiana . Podrían tolerar una inflación razonablemente alta ya que esto conduciría a un menor desempleo: habría una compensación entre inflación y desempleo. Por ejemplo, la política monetaria y/o la política fiscal podrían usarse para estimular la economía, elevando el producto interno bruto y reduciendo la tasa de desempleo. Moviéndose a lo largo de la curva de Phillips, esto conduciría a una tasa de inflación más alta, el costo de disfrutar de tasas de desempleo más bajas. [ cita requerida ] El economista James Forder cuestiona esta historia y argumenta que es un "mito de la curva de Phillips" inventado en la década de 1970. [14]
Desde 1974, se han otorgado siete Premios Nobel a economistas por, entre otras cosas, trabajos críticos con algunas variaciones de la curva de Phillips. Algunas de estas críticas se basan en la experiencia de los Estados Unidos durante la década de 1970, que tuvo períodos de alto desempleo y alta inflación al mismo tiempo. Entre los autores que recibieron esos premios se encuentran Thomas Sargent , Christopher Sims , Edmund Phelps , Edward Prescott , Robert A. Mundell , Robert E. Lucas , Milton Friedman y FA Hayek . [15]
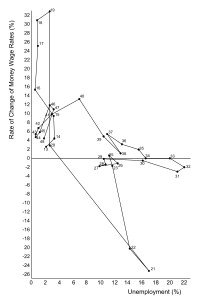
En la década de 1970, muchos países experimentaron altos niveles tanto de inflación como de desempleo, también conocidos como estanflación . Las teorías basadas en la curva de Phillips sugirieron que esto no ocurriría, y la curva fue atacada por un grupo de economistas encabezados por Milton Friedman . [7] Friedman sostuvo que la relación de la curva de Phillips era solo un fenómeno de corto plazo. Esto ocurrió ocho años después de que Samuelson y Solow [1960] escribieran: "Todo nuestro debate se ha expresado en términos de corto plazo, tratando de lo que podría suceder en los próximos años. Sin embargo, sería un error pensar que nuestro menú de la Figura 2 que relaciona el comportamiento de los precios obtenibles y el desempleo mantendrá su misma forma en el largo plazo. Lo que hagamos en términos de política durante los próximos años podría hacer que cambie de una manera definitiva". [12] Como Samuelson y Solow habían argumentado 8 años antes, Friedman dijo que, en el largo plazo, los trabajadores y los empleadores tendrán en cuenta la inflación, lo que dará como resultado contratos de trabajo que aumenten los salarios a tasas cercanas a la inflación anticipada. El desempleo comenzaría entonces a aumentar hasta su nivel anterior, pero con una inflación más alta. Esto implica que en el largo plazo no hay disyuntiva entre inflación y desempleo. Esto es importante porque implica que los bancos centrales no deberían fijar metas de desempleo por debajo de la tasa natural. [5]
Investigaciones más recientes sugieren que existe una disyuntiva moderada entre niveles bajos de inflación y desempleo. El trabajo de George Akerlof , William Dickens y George Perry [16] implica que si la inflación se reduce del dos al cero por ciento, el desempleo aumentará permanentemente en un 1,5 por ciento porque los trabajadores tienen una mayor tolerancia a los recortes salariales reales que a los nominales. Por ejemplo, es más probable que un trabajador acepte un aumento salarial del dos por ciento cuando la inflación es del tres por ciento, que un recorte salarial del uno por ciento cuando la tasa de inflación es cero.

La mayoría de los economistas ya no utilizan la curva de Phillips en su forma original porque era demasiado simplista. [17] Un análisis superficial de los datos de inflación y desempleo de Estados Unidos de 1953 a 1992 muestra que no hay una sola curva que se ajuste a los datos, pero hay tres agregaciones aproximadas (1955-71, 1974-84 y 1985-92), cada una de las cuales muestra una pendiente general descendente, pero en tres niveles muy diferentes, con cambios que ocurren abruptamente. Los datos de 1953-54 y 1972-73 no se agrupan fácilmente, y un análisis más formal postula hasta cinco grupos/curvas a lo largo del período. [5]
Sin embargo, las formas modificadas de la curva de Phillips que tienen en cuenta las expectativas inflacionarias siguen siendo influyentes. La teoría tiene varios nombres, con algunas variaciones en sus detalles, pero todas las versiones modernas distinguen entre efectos de corto y largo plazo sobre el desempleo. Los modelos modernos de la curva de Phillips incluyen tanto una curva de Phillips de corto plazo como una curva de Phillips de largo plazo. Esto se debe a que en el corto plazo, generalmente existe una relación inversa entre la inflación y la tasa de desempleo, como lo ilustra la curva de Phillips de corto plazo con pendiente negativa. En el largo plazo, esa relación se rompe y la economía finalmente regresa a la tasa natural de desempleo independientemente de la tasa de inflación. [18]
La "curva de Phillips de corto plazo" también se denomina "curva de Phillips aumentada por expectativas", ya que se desplaza hacia arriba cuando aumentan las expectativas inflacionarias, según afirmaron Edmund Phelps y Milton Friedman . A largo plazo, esto implica que la política monetaria no puede afectar al desempleo, que se ajusta de nuevo a su " tasa natural ", también llamada " NAIRU ". El popular libro de texto de Blanchard ofrece una presentación de libro de texto de la curva de Phillips aumentada por expectativas. [19]
Una ecuación como la curva de Phillips aumentada con expectativas también aparece en muchos modelos de equilibrio general dinámico estocástico neokeynesiano recientes . Como mencionó Keynes: "Un gobierno tiene que recordar, sin embargo, que incluso si un impuesto no está prohibido puede ser no rentable, y que una imposición media, en lugar de una extrema, rendirá la mayor ganancia". [20] En estos modelos macroeconómicos con precios rígidos , existe una relación positiva entre la tasa de inflación y el nivel de demanda, y por lo tanto una relación negativa entre la tasa de inflación y la tasa de desempleo. Esta relación a menudo se denomina "curva de Phillips neokeynesiana". Al igual que la curva de Phillips aumentada con expectativas, la curva de Phillips neokeynesiana implica que el aumento de la inflación puede reducir el desempleo temporalmente, pero no puede reducirlo permanentemente. Dos artículos influyentes que incorporan una curva de Phillips neokeynesiana son Clarida , Galí y Gertler (1999), [21] y Blanchard y Galí (2007). [22]
Existen al menos dos derivaciones matemáticas diferentes de la curva de Phillips. En primer lugar, está la versión tradicional o keynesiana . Luego, está la nueva versión clásica asociada con Robert E. Lucas Jr.
La literatura original sobre la curva de Phillips no se basó en la aplicación sin ayuda de la teoría económica, sino en generalizaciones empíricas. Después de eso, los economistas intentaron desarrollar teorías que se ajustaran a los datos.
La historia tradicional de la curva de Phillips comienza con una curva de Phillips de salarios, del tipo que describe el propio Phillips. Esta describe la tasa de crecimiento de los salarios monetarios ( gW ). Aquí y a continuación, el operador g es el equivalente de "la tasa porcentual de crecimiento" de la variable que sigue.
La "tasa salarial monetaria" ( W ) es una forma abreviada de representar los costos salariales monetarios totales por empleado de producción, incluidos los beneficios y los impuestos sobre la nómina. El enfoque se centra únicamente en los salarios monetarios de los trabajadores de producción, porque (como se analiza más adelante) estos costos son cruciales para las decisiones de fijación de precios de las empresas.
Esta ecuación nos dice que el crecimiento de los salarios monetarios aumenta con la tasa de tendencia de crecimiento de los salarios monetarios (indicada por el superíndice T ) y disminuye con la tasa de desempleo ( U ). Se supone que la función f aumenta monótonamente con U, de modo que la amortiguación de los aumentos de los salarios monetarios por el desempleo se muestra con el signo negativo en la ecuación anterior.
Hay varias posibles explicaciones detrás de esta ecuación. Una de las principales es que los salarios monetarios se fijan mediante negociaciones bilaterales en virtud de un monopolio bilateral parcial : a medida que aumenta la tasa de desempleo, todo el poder de negociación constante de los trabajadores disminuye, de modo que los trabajadores tienen menos capacidad para aumentar sus salarios ante la resistencia de los empleadores.
Durante la década de 1970, esta historia tuvo que modificarse, porque (como había sugerido el difunto Abba Lerner en la década de 1940) los trabajadores tratan de seguir el ritmo de la inflación. Desde la década de 1970, la ecuación se ha modificado para introducir el papel de las expectativas inflacionarias (o la tasa de inflación esperada, gP ex ). Esto produce la curva de Phillips de salarios aumentada con expectativas:
La introducción de expectativas inflacionarias en la ecuación implica que la inflación real puede retroalimentar las expectativas inflacionarias y, por lo tanto, causar más inflación. El difunto economista James Tobin denominó este último término "inercia inflacionaria", porque en el período actual existe una inflación que representa un impulso inflacionario remanente del pasado.
También implicó mucho más que expectativas, incluida la espiral de precios y salarios. En esta espiral, los empleadores tratan de proteger sus ganancias aumentando sus precios y los empleados tratan de seguir el ritmo de la inflación para proteger sus salarios reales. Este proceso puede retroalimentarse y convertirse en una profecía autocumplida.
El parámetro λ (que se supone constante durante cualquier período de tiempo) representa el grado en que los empleados pueden obtener aumentos salariales monetarios para mantenerse al día con la inflación esperada, evitando una caída de los salarios reales esperados. Por lo general, se supone que este parámetro es igual a 1 en el largo plazo.
Además, se modificó la función f () para introducir la idea de la tasa de desempleo no aceleradora de la inflación (NAIRU) o lo que a veces se denomina tasa de desempleo "natural" o tasa de desempleo umbral de inflación:
Aquí, U* es la NAIRU. Como se analiza más adelante, si U < U *, la inflación tiende a acelerarse. De manera similar, si U > U *, la inflación tiende a desacelerarse. Se supone que f (0) = 0, de modo que cuando U = U *, el término f desaparece de la ecuación.
En la ecuación ( 1 ), los roles de gW T y gP ex parecen ser redundantes, y desempeñan prácticamente el mismo papel. Sin embargo, suponiendo que λ es igual a la unidad, se puede ver que no lo son. Si la tasa de tendencia de crecimiento de los salarios monetarios es igual a cero, entonces el caso en que U es igual a U* implica que gW es igual a la inflación esperada. Es decir, los salarios reales esperados son constantes.
Sin embargo, en cualquier economía razonable, tener salarios reales esperados constantes solo podría ser compatible con salarios reales reales que se mantuvieran constantes a largo plazo. Esto no se ajusta a la experiencia económica de los Estados Unidos ni de ningún otro país industrial importante. Si bien los salarios reales no han aumentado mucho en los últimos años, ha habido aumentos importantes a lo largo de las décadas.
Una alternativa es suponer que la tasa de tendencia de crecimiento de los salarios monetarios es igual a la tasa de tendencia de crecimiento de la productividad laboral promedio ( Z ). Es decir:
En el supuesto ( 2 ), cuando U es igual a U* y λ es igual a la unidad, los salarios reales esperados aumentarían con la productividad laboral. Esto sería coherente con una economía en la que los salarios reales reales aumentan con la productividad laboral. Las desviaciones de las tendencias de los salarios reales respecto de las de la productividad laboral podrían explicarse haciendo referencia a otras variables del modelo.
A continuación, está el comportamiento de los precios. El supuesto estándar es que los mercados son imperfectamente competitivos , donde la mayoría de las empresas tienen cierto poder para fijar los precios. Por lo tanto, el modelo supone que la empresa promedio establece un precio unitario ( P ) como margen ( M ) sobre el costo unitario de mano de obra en la producción medido a una tasa estándar de utilización de la capacidad (por ejemplo, al 90 por ciento de uso de la planta y el equipo) y luego agrega el costo unitario de los materiales.
La estandarización implica ignorar posteriormente las desviaciones de la tendencia en la productividad laboral. Por ejemplo, supongamos que el crecimiento de la productividad laboral es el mismo que el de la tendencia y que la productividad actual es igual a su valor de tendencia:
El margen refleja tanto el grado de poder de mercado de la empresa como la medida en que se deben pagar los costos generales. Dicho de otro modo, si todo lo demás permanece igual, M aumenta con el poder de la empresa para fijar los precios o con un aumento de los costos generales en relación con los costos totales.
Así pues, el precio sigue esta ecuación:
El UMC es el costo unitario de las materias primas (costos totales de las materias primas divididos por la producción total). Por lo tanto, la ecuación puede reformularse de la siguiente manera:
Esta ecuación puede enunciarse nuevamente como:
Ahora, supongamos que tanto el margen de precio/costo promedio ( M ) como el CMU son constantes. Por otra parte, la productividad laboral crece, como antes. Por lo tanto, una ecuación que determina la tasa de inflación de precios ( gP ) es:
Luego, combinada con la curva de Phillips de salarios [ecuación 1] y el supuesto hecho anteriormente sobre el comportamiento tendencial de los salarios monetarios [ecuación 2], esta ecuación de precios-inflación nos da una simple curva de Phillips de precios aumentada con expectativas:
Algunos suponen que podemos simplemente sumar gUMC , la tasa de crecimiento de UMC , para representar el papel de los shocks de oferta (del tipo que asoló a los EE. UU. durante la década de 1970). Esto produce una curva de Phillips estándar de corto plazo:
El economista Robert J. Gordon lo ha llamado el "modelo del triángulo" porque explica el comportamiento inflacionario de corto plazo mediante tres factores: inflación de demanda (debida al bajo desempleo), inflación por shock de oferta ( gUMC ) y expectativas inflacionarias o inflación inercial.
Se supone que, a largo plazo , las expectativas inflacionarias alcanzan e igualan a la inflación real, de modo que gP = gP ex . Esto representa el equilibrio a largo plazo del ajuste de las expectativas. Parte de este ajuste puede implicar la adaptación de las expectativas a la experiencia con la inflación real. Otra parte puede implicar conjeturas hechas por las personas en la economía basadas en otra evidencia. (Esta última idea nos dio la noción de las llamadas expectativas racionales ).
El equilibrio expectacional nos da la curva de Phillips de largo plazo. Primero, con λ menor que la unidad:
Esto no es más que una versión más pronunciada de la curva de Phillips de corto plazo anterior. La inflación aumenta a medida que el desempleo cae, mientras que esta conexión es más fuerte. Es decir, una tasa de desempleo baja (menor que U* ) estará asociada con una tasa de inflación más alta en el largo plazo que en el corto plazo. Esto ocurre porque la situación real de mayor inflación observada en el corto plazo retroalimenta para aumentar las expectativas inflacionarias, lo que a su vez aumenta aún más la tasa de inflación. De manera similar, las tasas de desempleo altas (mayores que U* ) conducen a tasas de inflación bajas. Estas a su vez alientan expectativas inflacionarias más bajas, de modo que la inflación misma cae nuevamente.
Esta lógica se aplica aún más si λ es igual a la unidad, es decir, si los trabajadores pueden proteger completamente sus salarios de la inflación esperada, incluso en el corto plazo. Ahora, la ecuación del modelo triangular se convierte en:
Si suponemos además (como parece razonable) que no hay shocks de oferta a largo plazo, esto se puede simplificar de la siguiente manera:
Todas las hipótesis implican que, a largo plazo, solo existe una tasa de desempleo posible, U*, en cualquier momento. Esta singularidad explica por qué algunos llaman a esta tasa de desempleo "natural".
Para comprender y criticar verdaderamente la singularidad de U* , se necesita un modelo más sofisticado y realista. Por ejemplo, podríamos introducir la idea de que los trabajadores de distintos sectores presionan para conseguir aumentos salariales monetarios similares a los de otros sectores. O podríamos hacer que el modelo sea aún más realista. Un aspecto importante que debemos tener en cuenta es la determinación del margen , M.
La ecuación de la curva de Phillips se puede derivar de la función de oferta agregada de Lucas (a corto plazo) . El enfoque de Lucas es muy diferente del enfoque tradicional. En lugar de comenzar con datos empíricos, comenzó con un modelo económico clásico que seguía principios económicos muy simples.
Comencemos con la función de oferta agregada :
donde Y es el logaritmo del nivel de producción real , es el logaritmo del nivel de producción "natural", es una constante positiva, es el logaritmo del nivel de precios real y es el logaritmo del nivel de precios esperado . Lucas supone que tiene un valor único.
Obsérvese que esta ecuación indica que cuando las expectativas de inflación futura (o, más correctamente, el nivel de precios futuro) son totalmente exactas , el último término desaparece, de modo que la producción real es igual al llamado nivel "natural" del PIB real. Esto significa que en la curva de oferta agregada de Lucas, la única razón por la que el PIB real real debería desviarse del potencial -y la tasa de desempleo real debería desviarse de la tasa "natural"- es debido a expectativas incorrectas de lo que va a suceder con los precios en el futuro. (La idea fue expresada por primera vez por Keynes , Teoría general , Capítulo 20, Sección III, párrafo 4).
Esto difiere de otras concepciones de la curva de Phillips, en las que el fracaso en alcanzar el nivel "natural" de producción puede deberse a la imperfección o incompletitud de los mercados, la rigidez de los precios y otras cuestiones similares. En la concepción no basada en Lucas, las expectativas incorrectas pueden contribuir a la falla de la demanda agregada, pero no son la única causa. Para los seguidores "nuevos clásicos" de Lucas, se supone que los mercados son perfectos y siempre alcanzan el equilibrio (dadas las expectativas inflacionarias).
Reordenamos la ecuación en:
A continuación añadimos shocks exógenos inesperados a la oferta mundial :
Restando los niveles de precios del año pasado obtendremos tasas de inflación, porque
y
donde y son la inflación y la inflación esperada respectivamente.
También existe una relación negativa entre la producción y el desempleo (como lo expresa la ley de Okun ). Por lo tanto, utilizando
donde es una constante positiva, es el desempleo y es la tasa natural de desempleo o NAIRU , llegamos a la forma final de la curva de Phillips de corto plazo:
Esta ecuación, que representa la tasa de inflación frente al desempleo, da como resultado la curva de pendiente descendente en el diagrama que caracteriza la curva de Phillips.
La curva de Phillips neokeynesiana fue derivada originalmente por Roberts en 1995, [23] y desde entonces se ha utilizado en la mayoría de los modelos DSGE neokeynesianos de última generación, como el de Clarida, Galí y Gertler (2000). [24] [25]
dónde
Las expectativas actuales de inflación del próximo período se incorporan como .

En la década de 1970, surgieron nuevas teorías, como las expectativas racionales y la NAIRU (tasa de desempleo no aceleradora de la inflación) para explicar cómo podía producirse la estanflación . Esta última teoría, también conocida como la " tasa natural de desempleo ", distinguía entre la curva de Phillips de "corto plazo" y la de "largo plazo". La curva de Phillips de corto plazo parecía una curva de Phillips normal, pero se desplazaba a largo plazo a medida que cambiaban las expectativas. A largo plazo, sólo una única tasa de desempleo (la NAIRU o tasa "natural") era compatible con una tasa de inflación estable. La curva de Phillips de largo plazo era, por tanto, vertical, de modo que no había disyuntiva entre inflación y desempleo. Milton Friedman en 1976 y Edmund Phelps en 2006 ganaron el Premio Nobel de Economía en parte por este trabajo. [26] [27] Sin embargo, el argumento de las expectativas era de hecho muy ampliamente comprendido (aunque no formalmente) antes del trabajo de Friedman y Phelps sobre él. [28]
En el diagrama, la curva de Phillips de largo plazo es la línea roja vertical. La teoría de la NAIRU dice que cuando el desempleo se encuentra en la tasa definida por esta línea, la inflación será estable. Sin embargo, en el corto plazo, las autoridades se enfrentarán a una disyuntiva entre inflación y tasa de desempleo marcada por la "Curva de Phillips de Corto Plazo Inicial" en el gráfico. Por lo tanto, las autoridades pueden reducir la tasa de desempleo temporalmente, moviéndose del punto A al punto B mediante una política expansiva. Sin embargo, según la NAIRU, explotar esta disyuntiva de corto plazo aumentará las expectativas de inflación, desplazando la curva de corto plazo hacia la derecha hasta la "nueva curva de Phillips de corto plazo" y moviendo el punto de equilibrio de B a C. Por lo tanto, la reducción del desempleo por debajo de la "Tasa Natural" será temporal y conducirá únicamente a una mayor inflación en el largo plazo.
Como la curva de corto plazo se desplaza hacia afuera debido al intento de reducir el desempleo, la política expansiva termina empeorando la disyuntiva explotable entre desempleo e inflación. Es decir, resulta en más inflación para cada tasa de desempleo de corto plazo. El nombre "NAIRU" surge porque con un desempleo real por debajo de ella, la inflación se acelera, mientras que con un desempleo por encima de ella, la inflación se desacelera. Con una tasa real igual a ella, la inflación es estable, ni se acelera ni se desacelera. Un uso práctico de este modelo fue explicar la estanflación, que confundía a la curva de Phillips tradicional.
La teoría de las expectativas racionales decía que las expectativas de inflación eran iguales a lo que realmente ocurría, con algunos errores menores y temporales. Esto, a su vez, sugería que el período de corto plazo era tan corto que era inexistente: cualquier esfuerzo por reducir el desempleo por debajo de la NAIRU, por ejemplo, causaría inmediatamente un aumento de las expectativas inflacionarias y, por lo tanto, implicaría que la política fracasaría. El desempleo nunca se desviaría de la NAIRU, excepto debido a errores aleatorios y transitorios en la elaboración de expectativas sobre las tasas de inflación futuras. Desde esta perspectiva, cualquier desviación de la tasa de desempleo real respecto de la NAIRU era una ilusión.
Sin embargo, en los años 1990 en Estados Unidos se hizo cada vez más evidente que la NAIRU no tenía un equilibrio único y podía cambiar de manera impredecible. A fines de los años 1990, la tasa de desempleo real cayó por debajo del 4% de la fuerza laboral, mucho más baja que casi todas las estimaciones de la NAIRU. Pero la inflación se mantuvo muy moderada en lugar de acelerarse. De modo que, así como la curva de Phillips se había convertido en tema de debate, también lo hizo la NAIRU.
Además, el concepto de expectativas racionales se puso en tela de juicio cuando se hizo evidente que el supuesto principal de los modelos basados en él era que existe un único equilibrio en la economía, que se establece de antemano y se determina independientemente de las condiciones de la demanda. La experiencia de los años 1990 sugiere que este supuesto no se puede sostener.
Para Milton Friedman existe una correlación de corto plazo entre los shocks inflacionarios y el empleo. Cuando se produce una sorpresa inflacionaria, los trabajadores se ven engañados y aceptan salarios más bajos porque no ven la caída de los salarios reales de inmediato. Las empresas los contratan porque ven que la inflación permite mayores ganancias para los salarios nominales dados. Este es un movimiento a lo largo de la curva de Phillips como en el caso del cambio A . Finalmente, los trabajadores descubren que los salarios reales han caído, por lo que presionan para obtener salarios monetarios más altos. Esto hace que la curva de Phillips se desplace hacia arriba y hacia la derecha, como en el caso de B . Algunas investigaciones subrayan que algunos supuestos implícitos y serios están en realidad en el trasfondo de la curva de Phillips de Friedman. Esta asimetría de la información y un patrón especial de flexibilidad de precios y salarios son necesarios si uno quiere mantener el mecanismo contado por Friedman. Sin embargo, como se argumenta, estas presunciones permanecen completamente ocultas y teóricamente infundadas por Friedman. [29]
Robert J. Gordon, de la Universidad Northwestern, ha analizado la curva de Phillips para producir lo que él llama el modelo triangular , en el que la tasa de inflación real está determinada por la suma de
El último refleja las expectativas inflacionarias y la espiral de precios y salarios . Los shocks de oferta y los cambios en la inflación incorporada son los principales factores que desplazan la curva de Phillips de corto plazo y modifican la disyuntiva. En esta teoría, no son sólo las expectativas inflacionarias las que pueden causar estanflación. Por ejemplo, la pronunciada subida de los precios del petróleo durante la década de 1970 podría tener este resultado.
Los cambios en la inflación incorporada siguen la lógica de ajuste parcial detrás de la mayoría de las teorías de la NAIRU:
Entre estos dos extremos se encuentra la tasa de desempleo no inflacionario (NAIRU), en la que la curva de Phillips no tiene ninguna tendencia inherente a desplazarse, de modo que la tasa de inflación es estable. Sin embargo, parece haber un rango intermedio entre "alta" y "baja" en el que la inflación incorporada se mantiene estable. Los extremos de este "rango de tasas de desempleo que no aceleran la inflación" cambian con el tiempo.