Ecuación cuadrática

Ecuación polinómica de grado dos

En matemáticas , una ecuación cuadrática (del latín quadratus  ' cuadrado ') es una ecuación que se puede reorganizar en forma estándar como ^[1] donde la variable x representa un número desconocido, y a , b y c representan números conocidos, donde a ≠ 0 . (Si a = 0 y b ≠ 0 entonces la ecuación es lineal , no cuadrática.) Los números a , b y c son los coeficientes de la ecuación y se pueden distinguir llamándolos respectivamente, el coeficiente cuadrático , el coeficiente lineal y el coeficiente constante o término libre . ^[2] $${\displaystyle ax^{2}+bx+c=0\,,}$$

Los valores de x que satisfacen la ecuación se denominan soluciones de la ecuación y raíces o ceros de la función cuadrática en su lado izquierdo. Una ecuación cuadrática tiene como máximo dos soluciones. Si solo hay una solución, se dice que es una raíz doble . Si todos los coeficientes son números reales , hay dos soluciones reales, o una única raíz doble real, o dos soluciones complejas que son conjugadas complejas entre sí. Una ecuación cuadrática siempre tiene dos raíces, si se incluyen raíces complejas y una raíz doble se cuenta como dos. Una ecuación cuadrática se puede factorizar en una ecuación equivalente ^[3] donde r y s son las soluciones para x . $${\displaystyle ax^{2}+bx+c=a(x-r)(x-s)=0}$$

La fórmula cuadrática expresa las soluciones en términos de a , b y c . Completar el cuadrado es una de las diversas formas de obtener la fórmula. $${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$$

Las soluciones a problemas que pueden expresarse en términos de ecuaciones cuadráticas se conocían ya en el año 2000 a. C. ^{[4] [5]}

Debido a que la ecuación cuadrática involucra solo una incógnita, se la llama " univariante ". La ecuación cuadrática contiene solo potencias de x que son números enteros no negativos y, por lo tanto, es una ecuación polinómica . En particular, es una ecuación polinómica de segundo grado , ya que la mayor potencia es dos.

Resolver la ecuación cuadrática

Figura 1. Gráficos de la función cuadrática y = ax ² + bx + c , variando cada coeficiente por separado mientras que los demás coeficientes se mantienen fijos (en los valores a  = 1, b  = 0, c  = 0)

Una ecuación cuadrática cuyos coeficientes son números reales puede tener cero, una o dos soluciones reales distintas, también llamadas raíces . Cuando solo hay una raíz distinta, se puede interpretar como dos raíces con el mismo valor, llamadas raíz doble . Cuando no hay raíces reales, los coeficientes se pueden considerar como números complejos con parte imaginaria cero , y la ecuación cuadrática aún tiene dos raíces de valor complejo, conjugadas complejas entre sí con una parte imaginaria distinta de cero. Una ecuación cuadrática cuyos coeficientes son números complejos arbitrarios siempre tiene dos raíces de valor complejo que pueden ser distintas o no.

Las soluciones de una ecuación cuadrática se pueden encontrar mediante varios métodos alternativos.

Factoraje por inspección

Es posible expresar una ecuación cuadrática ax ² + bx + c = 0 como un producto ( px + q )( rx + s ) = 0 . En algunos casos, es posible, mediante una simple inspección, determinar valores de p , q , r y s que hagan que las dos formas sean equivalentes entre sí. Si la ecuación cuadrática se escribe en la segunda forma, entonces la "Propiedad del factor cero" establece que la ecuación cuadrática se satisface si px + q = 0 o rx + s = 0 . Resolver estas dos ecuaciones lineales proporciona las raíces de la ecuación cuadrática.

Para la mayoría de los estudiantes, la factorización por inspección es el primer método de resolución de ecuaciones cuadráticas al que están expuestos. ^{[6] : 202–207} Si se da una ecuación cuadrática en la forma x ² + bx + c = 0 , la factorización buscada tiene la forma ( x + q )( x + s ) , y uno tiene que encontrar dos números q y s que sumen b y cuyo producto sea c (esto a veces se llama "regla de Vieta" ^[7] y está relacionada con las fórmulas de Vieta ). Como ejemplo, x ² + 5 x + 6 se factoriza como ( x + 3)( x + 2) . El caso más general donde a no es igual a 1 puede requerir un esfuerzo considerable en prueba y error de conjeturas y comprobaciones, suponiendo que se puede factorizar por inspección.

Salvo casos especiales como cuando b = 0 o c = 0 , la factorización por inspección solo funciona para ecuaciones cuadráticas que tienen raíces racionales. Esto significa que la gran mayoría de ecuaciones cuadráticas que surgen en aplicaciones prácticas no se pueden resolver mediante factorización por inspección. ^{[6] : 207}

Completando el cuadrado

Figura 2. Para la función cuadrática y = x ² − x − 2 , los puntos donde la gráfica cruza el eje x , x = −1 y x = 2 , son las soluciones de la ecuación cuadrática x ² − x − 2 = 0 .

El proceso de completar el cuadrado hace uso de la identidad algebraica que representa un algoritmo bien definido que se puede utilizar para resolver cualquier ecuación cuadrática. ^{[6] : 207} Comenzando con una ecuación cuadrática en forma estándar, ax ² + bx + c = 0 $${\displaystyle x^{2}+2hx+h^{2}=(x+h)^{2},}$$

1. Divida cada lado por a , el coeficiente del término al cuadrado.
2. Resta el término constante c / a de ambos lados.
3. Suma el cuadrado de la mitad de b / a , el coeficiente de x , a ambos lados. Esto "completa el cuadrado", convirtiendo el lado izquierdo en un cuadrado perfecto.
4. Escribe el lado izquierdo como un cuadrado y simplifica el lado derecho si es necesario.
5. Producir dos ecuaciones lineales igualando la raíz cuadrada del lado izquierdo con las raíces cuadradas positivas y negativas del lado derecho.
6. Resuelve cada una de las dos ecuaciones lineales.

Ilustramos el uso de este algoritmo resolviendo 2 x ² + 4 x − 4 = 0 $${\displaystyle 2x^{2}+4x-4=0}$$ $${\displaystyle \ x^{2}+2x-2=0}$$ $${\displaystyle \ x^{2}+2x=2}$$ $${\displaystyle \ x^{2}+2x+1=2+1}$$ $${\displaystyle \left(x+1\right)^{2}=3}$$ $${\displaystyle \ x+1=\pm {\sqrt {3}}}$$ $${\displaystyle \ x=-1\pm {\sqrt {3}}}$$

El símbolo más-menos "±" indica que tanto como son soluciones de la ecuación cuadrática. ^[8] ${\textstyle x=-1+{\sqrt {3}}}$ ${\textstyle x=-1-{\sqrt {3}}}$

Fórmula cuadrática y su derivación

Completar el cuadrado se puede utilizar para derivar una fórmula general para resolver ecuaciones cuadráticas, llamada fórmula cuadrática. ^[9] A continuación se resumirá brevemente la prueba matemática . ^[10] Se puede ver fácilmente, por expansión polinomial , que la siguiente ecuación es equivalente a la ecuación cuadrática: Tomando la raíz cuadrada de ambos lados y despejando x , se obtiene: $${\displaystyle \left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}.}$$ $${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.}$$

Algunas fuentes, en particular las más antiguas, utilizan parametrizaciones alternativas de la ecuación cuadrática, como ax ² + 2 bx + c = 0 o ax ² − 2 bx + c = 0  , ^[11] donde b tiene una magnitud de la mitad de la más común, posiblemente con signo opuesto. Estas dan como resultado formas ligeramente diferentes para la solución, pero por lo demás son equivalentes.

En la literatura se pueden encontrar varias derivaciones alternativas . Estas demostraciones son más sencillas que el método estándar de completar el cuadrado, representan aplicaciones interesantes de otras técnicas de uso frecuente en álgebra o brindan información sobre otras áreas de las matemáticas.

Una fórmula cuadrática menos conocida, como la utilizada en el método de Muller , proporciona las mismas raíces a través de la ecuación Esto se puede deducir de la fórmula cuadrática estándar mediante las fórmulas de Vieta , que afirman que el producto de las raíces es c / a . También se deduce de dividir la ecuación cuadrática dando resolviendo esto para y luego invirtiendo. $${\displaystyle x={\frac {2c}{-b\pm {\sqrt {b^{2}-4ac}}}}.}$$ ${\displaystyle x^{2}}$ ${\displaystyle cx^{-2}+bx^{-1}+a=0,}$ ${\displaystyle x^{-1},}$

Una propiedad de esta forma es que produce una raíz válida cuando a = 0 , mientras que la otra raíz contiene una división por cero, porque cuando a = 0 , la ecuación cuadrática se convierte en una ecuación lineal, que tiene una raíz. Por el contrario, en este caso, la fórmula más común tiene una división por cero para una raíz y una forma indeterminada 0/0 para la otra raíz. Por otro lado, cuando c = 0 , la fórmula más común produce dos raíces correctas, mientras que esta forma produce la raíz cero y una forma indeterminada 0/0 .

Cuando ni a ni c son cero, la igualdad entre la fórmula cuadrática estándar y el método de Muller se puede verificar mediante la multiplicación cruzada , y de manera similar para la otra elección de signos. $${\displaystyle {\frac {2c}{-b-{\sqrt {b^{2}-4ac}}}}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\,,}$$

Ecuación cuadrática reducida

A veces es conveniente reducir una ecuación cuadrática de modo que su coeficiente principal sea uno. Esto se hace dividiendo ambos lados por a , lo que siempre es posible ya que a no es cero. Esto produce la ecuación cuadrática reducida : ^[12]

$${\displaystyle x^{2}+px+q=0,}$$

donde p = b / a y q = c / a . Esta ecuación polinómica mónica tiene las mismas soluciones que la original.

La fórmula cuadrática para las soluciones de la ecuación cuadrática reducida, escrita en términos de sus coeficientes, es $${\displaystyle x=-{\frac {p}{2}}\pm {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}\,.}$$

Discriminante

Figura 3. Signos discriminantes

En la fórmula cuadrática, la expresión debajo del signo de raíz cuadrada se denomina discriminante de la ecuación cuadrática y, a menudo, se representa mediante una D mayúscula o una delta griega mayúscula : ^[13] Una ecuación cuadrática con coeficientes reales puede tener una o dos raíces reales distintas, o dos raíces complejas distintas. En este caso, el discriminante determina el número y la naturaleza de las raíces. Hay tres casos: $${\displaystyle \Delta =b^{2}-4ac.}$$

• Si el discriminante es positivo, entonces hay dos raíces distintas , ambas son números reales. Para ecuaciones cuadráticas con coeficientes racionales , si el discriminante es un número cuadrado , entonces las raíces son racionales; en otros casos, pueden ser irracionales cuadráticas . $${\displaystyle {\frac {-b+{\sqrt {\Delta }}}{2a}}\quad {\text{and}}\quad {\frac {-b-{\sqrt {\Delta }}}{2a}},}$$
• Si el discriminante es cero, entonces hay exactamente una raíz real , a veces llamada raíz repetida o doble , o dos raíces iguales. ${\displaystyle -{\frac {b}{2a}},}$
• Si el discriminante es negativo, entonces no hay raíces reales. En cambio, hay dos raíces complejas distintas (no reales) ^[14] que son conjugadas complejas entre sí. En estas expresiones, i es la unidad imaginaria . $${\displaystyle -{\frac {b}{2a}}+i{\frac {\sqrt {-\Delta }}{2a}}\quad {\text{and}}\quad -{\frac {b}{2a}}-i{\frac {\sqrt {-\Delta }}{2a}},}$$

Por lo tanto, las raíces son distintas si y sólo si el discriminante es distinto de cero, y las raíces son reales si y sólo si el discriminante es no negativo.

Interpretación geométrica

Visualización de las raíces complejas de y = ax ² + bx + c : la parábola se gira 180° alrededor de su vértice ( naranja ). Sus puntos de corte con el eje x se giran 90° alrededor de su punto medio y el plano cartesiano se interpreta como el plano complejo ( verde ). ^[15]

La función f ( x ) = ax ² + bx + c es una función cuadrática . ^[16] La gráfica de cualquier función cuadrática tiene la misma forma general, que se llama parábola . La ubicación y el tamaño de la parábola, y cómo se abre, dependen de los valores de a , b y c . Si a > 0 , la parábola tiene un punto mínimo y se abre hacia arriba. Si a < 0 , la parábola tiene un punto máximo y se abre hacia abajo. El punto extremo de la parábola, ya sea mínimo o máximo, corresponde a su vértice . La coordenada x del vértice estará ubicada en , y la coordenada y del vértice se puede encontrar sustituyendo este valor de x en la función. La intersección con el eje y se encuentra en el punto (0, c ) . ${\displaystyle \scriptstyle x={\tfrac {-b}{2a}}}$

Las soluciones de la ecuación cuadrática ax ² + bx + c = 0 corresponden a las raíces de la función f ( x ) = ax ² + bx + c , ya que son los valores de x para los cuales f ( x ) = 0 . Si a , b y c son números reales y el dominio de f es el conjunto de números reales, entonces las raíces de f son exactamente las coordenadas x de los puntos donde la gráfica toca el eje x . Si el discriminante es positivo, la gráfica toca el eje x en dos puntos; si es cero, la gráfica toca en un punto; y si es negativo, la gráfica no toca el eje x .

Factorización cuadrática

El término es un factor del polinomio si y solo si r es una raíz de la ecuación cuadrática. De la fórmula cuadrática se deduce que En el caso especial b ² = 4 ac donde la cuadrática tiene solo una raíz distinta ( es decir , el discriminante es cero), el polinomio cuadrático se puede factorizar como $${\displaystyle x-r}$$ $${\displaystyle ax^{2}+bx+c}$$ $${\displaystyle ax^{2}+bx+c=0.}$$ $${\displaystyle ax^{2}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right).}$$ $${\displaystyle ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}.}$$

Solución gráfica

Figura 4. Cálculo con calculadora gráfica de una de las dos raíces de la ecuación cuadrática 2 x ² + 4 x − 4 = 0. Aunque la pantalla muestra solo cinco cifras significativas de precisión, el valor obtenido de xc es 0,732050807569, con una precisión de doce cifras significativas.

Una función cuadrática sin raíz real: y = ( x − 5) ² + 9 . El "3" es la parte imaginaria de la intersección con el eje x . La parte real es la coordenada x del vértice. Por lo tanto, las raíces son 5 ± 3 i .

Las soluciones de la ecuación cuadrática se pueden deducir de la gráfica de la función cuadrática que es una parábola . $${\displaystyle ax^{2}+bx+c=0}$$ $${\displaystyle f(x)=ax^{2}+bx+c,}$$

Si la parábola interseca el eje x en dos puntos, hay dos raíces reales , que son las coordenadas x de estos dos puntos (también llamadas intersección con el eje x ).

Si la parábola es tangente al eje x , existe una raíz doble, que es la coordenada x del punto de contacto entre la gráfica y la parábola.

Si la parábola no corta el eje x , hay dos raíces conjugadas complejas . Aunque estas raíces no se pueden visualizar en el gráfico, sí se pueden visualizar sus partes reales e imaginarias . ^[17]

Sean h y k respectivamente la coordenada x y la coordenada y del vértice de la parábola (es decir, el punto con la coordenada y máxima o mínima) . La función cuadrática puede reescribirse Sea d la distancia entre el punto de la coordenada y 2 k en el eje de la parábola, y un punto en la parábola con la misma coordenada y (véase la figura; hay dos puntos de este tipo, que dan la misma distancia, debido a la simetría de la parábola). Entonces la parte real de las raíces es h , y su parte imaginaria es ± d . Es decir, las raíces son o en el caso del ejemplo de la figura $${\displaystyle y=a(x-h)^{2}+k.}$$ $${\displaystyle h+id\quad {\text{and}}\quad h-id,}$$ $${\displaystyle 5+3i\quad {\text{and}}\quad 5-3i.}$$

Cómo evitar la pérdida de importancia

Aunque la fórmula cuadrática proporciona una solución exacta, el resultado no es exacto si se aproximan números reales durante el cálculo, como es habitual en el análisis numérico , donde los números reales se aproximan mediante números de punto flotante (llamados "reales" en muchos lenguajes de programación ). En este contexto, la fórmula cuadrática no es completamente estable .

Esto ocurre cuando las raíces tienen diferente orden de magnitud o, equivalentemente, cuando b ² y b ² − 4 ac son de magnitud cercana. En este caso, la resta de dos números casi iguales provocará pérdida de significancia o cancelación catastrófica en la raíz más pequeña. Para evitar esto, la raíz que es más pequeña en magnitud, r , se puede calcular como donde R es la raíz que es más grande en magnitud. Esto es equivalente a usar la fórmula ${\displaystyle (c/a)/R}$

$${\displaystyle x={\frac {-2c}{b\pm {\sqrt {b^{2}-4ac}}}}}$$

usando el signo más si y el signo menos si ${\displaystyle b>0}$ ${\displaystyle b<0.}$

Una segunda forma de cancelación puede ocurrir entre los términos b ² y 4 ac del discriminante, es decir, cuando las dos raíces están muy próximas. Esto puede llevar a la pérdida de hasta la mitad de las cifras significativas correctas en las raíces. ^{[11] [18]}

Ejemplos y aplicaciones

La trayectoria del saltador del acantilado es parabólica porque el desplazamiento horizontal es una función lineal del tiempo , mientras que el desplazamiento vertical es una función cuadrática del tiempo . Como resultado, la trayectoria sigue la ecuación cuadrática , donde y son los componentes horizontal y vertical de la velocidad original, a es la aceleración gravitacional y h es la altura original. El valor de a debe considerarse negativo aquí, ya que su dirección (hacia abajo) es opuesta a la medida de la altura (hacia arriba). ${\displaystyle x=v_{x}t}$ ${\displaystyle y={\tfrac {1}{2}}at^{2}+v_{y}t+h}$ ${\displaystyle y={\tfrac {a}{2v_{x}^{2}}}x^{2}+{\tfrac {v_{y}}{v_{x}}}x+h}$ ${\displaystyle v_{x}}$ ${\displaystyle v_{y}}$

La proporción áurea se encuentra como la solución positiva de la ecuación cuadrática. ${\displaystyle x^{2}-x-1=0.}$

Las ecuaciones del círculo y de otras secciones cónicas ( elipses , parábolas e hipérbolas ) son ecuaciones cuadráticas en dos variables.

Dado el coseno o el seno de un ángulo, encontrar el coseno o el seno del ángulo que es la mitad de grande implica resolver una ecuación cuadrática.

El proceso de simplificar expresiones que involucran la raíz cuadrada de una expresión que involucra la raíz cuadrada de otra expresión implica encontrar las dos soluciones de una ecuación cuadrática.

El teorema de Descartes establece que por cada cuatro círculos que se besan (tangentes entre sí), sus radios satisfacen una ecuación cuadrática particular.

La ecuación dada por el teorema de Fuss , que da la relación entre el radio del círculo inscrito de un cuadrilátero bicéntrico , el radio de su círculo circunscrito y la distancia entre los centros de esos círculos, puede expresarse como una ecuación cuadrática para la cual la distancia entre los centros de los dos círculos en términos de sus radios es una de las soluciones. La otra solución de la misma ecuación en términos de los radios relevantes da la distancia entre el centro del círculo circunscrito y el centro del círculo ex tangencial de un cuadrilátero ex tangencial .

Los puntos críticos de una función cúbica y los puntos de inflexión de una función cuártica se encuentran resolviendo una ecuación cuadrática.

En física , para un movimiento con aceleración constante , el desplazamiento o posición de un cuerpo en movimiento se puede expresar como una función cuadrática del tiempo dada la posición inicial y la velocidad inicial : . ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle x_{0}}$ ${\displaystyle v_{0}}$ ${\textstyle x=x_{0}+v_{0}t+{\frac {1}{2}}at^{2}}$

En química , el pH de una solución de ácido débil se puede calcular a partir del logaritmo negativo en base 10 de la raíz positiva de una ecuación cuadrática en términos de la constante de acidez y la concentración analítica del ácido.

Historia

Los matemáticos babilónicos , ya en el año 2000 a. C. (como se muestra en tablillas de arcilla de la antigua Babilonia ), podían resolver problemas relacionados con las áreas y los lados de los rectángulos. Hay evidencia que data de este algoritmo en la Tercera Dinastía de Ur . ^[19] En la notación moderna, los problemas generalmente implicaban resolver un par de ecuaciones simultáneas de la forma: que es equivalente a la afirmación de que x e y son las raíces de la ecuación: ^{[20] : 86} $${\displaystyle x+y=p,\ \ xy=q,}$$ $${\displaystyle z^{2}+q=pz.}$$

Los pasos dados por los escribas babilónicos para resolver el problema del rectángulo mencionado anteriormente, en términos de x e y , fueron los siguientes:

1. Calcular la mitad de p .
2. Elevar al cuadrado el resultado.
3. Restar q .
4. Encuentra la raíz cuadrada (positiva) usando una tabla de cuadrados.
5. Sume los resultados de los pasos (1) y (4) para obtener x .

En notación moderna, esto significa calcular , que es equivalente a la fórmula cuadrática moderna para la raíz real más grande (si la hay) con a = 1 , b = − p y c = q . ${\displaystyle x={\frac {p}{2}}+{\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}}$ ${\displaystyle x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}}$

Los métodos geométricos se utilizaron para resolver ecuaciones cuadráticas en Babilonia, Egipto, Grecia, China e India. El Papiro egipcio de Berlín , que data del Reino Medio (2050 a. C. a 1650 a. C.), contiene la solución de una ecuación cuadrática de dos términos. ^[21] Los matemáticos babilónicos de alrededor del 400 a. C. y los matemáticos chinos de alrededor del 200 a. C. utilizaron métodos geométricos de disección para resolver ecuaciones cuadráticas con raíces positivas. ^{[22] [23]} Las reglas para ecuaciones cuadráticas se dieron en Los nueve capítulos sobre el arte matemático , un tratado chino sobre matemáticas. ^{[23] [24]} Estos primeros métodos geométricos no parecen haber tenido una fórmula general. Euclides , el matemático griego , produjo un método geométrico más abstracto alrededor del 300 a. C. Con un enfoque puramente geométrico, Pitágoras y Euclides crearon un procedimiento general para encontrar soluciones de la ecuación cuadrática. En su obra Arithmetica , el matemático griego Diofanto resolvió la ecuación cuadrática, pero dando sólo una raíz, incluso cuando ambas raíces eran positivas. ^[25]

En 628 d. C., Brahmagupta , un matemático indio , dio en su libro Brāhmasphuṭasiddhānta la primera solución explícita (aunque todavía no completamente general) de la ecuación cuadrática ax ² + bx = c de la siguiente manera: "Al número absoluto multiplicado por cuatro veces el [coeficiente del] cuadrado, se suma el cuadrado del [coeficiente del] término medio; la raíz cuadrada del mismo, menos el [coeficiente del] término medio, siendo dividido por dos veces el [coeficiente del] cuadrado es el valor". ^[26] Esto es equivalente a El Manuscrito Bakhshali escrito en la India en el siglo VII d. C. contenía una fórmula algebraica para resolver ecuaciones cuadráticas, así como ecuaciones lineales indeterminadas (originalmente de tipo ax / c = y ). Muhammad ibn Musa al-Khwarizmi (siglo IX) desarrolló un conjunto de fórmulas que funcionaban para soluciones positivas. Al-Khwarizmi va más allá al proporcionar una solución completa a la ecuación cuadrática general, aceptando una o dos respuestas numéricas para cada ecuación cuadrática, mientras proporciona pruebas geométricas en el proceso. ^[27] También describió el método de completar el cuadrado y reconoció que el discriminante debe ser positivo, ^{[27] [28] : 230} lo que fue demostrado por su contemporáneo 'Abd al-Hamīd ibn Turk (Asia Central, siglo IX) quien dio figuras geométricas para demostrar que si el discriminante es negativo, una ecuación cuadrática no tiene solución. ^{[28] : 234} Si bien el propio al-Khwarizmi no aceptó soluciones negativas, los matemáticos islámicos posteriores que lo sucedieron aceptaron soluciones negativas, ^{[27] : 191} así como números irracionales como soluciones. ^[29] Abū Kāmil Shujā ibn Aslam (Egipto, siglo X) en particular fue el primero en aceptar números irracionales (a menudo en forma de raíz cuadrada , raíz cúbica o raíz cuarta ) como soluciones a ecuaciones cuadráticas o como coeficientes en una ecuación. ^[30] El matemático indio del siglo IX Sridhara escribió reglas para resolver ecuaciones cuadráticas. ^[31] $${\displaystyle x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}.}$$

El matemático judío Abraham bar Hiyya Ha-Nasi (siglo XII, España) fue autor del primer libro europeo que incluía la solución completa de la ecuación cuadrática general. ^[32] Su solución se basó en gran medida en el trabajo de Al-Khwarizmi. ^[27] El escrito del matemático chino Yang Hui (1238-1298 d. C.) es el primero conocido en el que aparecen ecuaciones cuadráticas con coeficientes negativos de 'x', aunque él atribuye esto al anterior Liu Yi. ^[33] En 1545, Gerolamo Cardano recopiló los trabajos relacionados con las ecuaciones cuadráticas. La fórmula cuadrática que cubre todos los casos fue obtenida por primera vez por Simon Stevin en 1594. ^[34] En 1637, René Descartes publicó La Géométrie que contiene la fórmula cuadrática en la forma que conocemos hoy.

Temas avanzados

Métodos alternativos de cálculo de raíces

Las fórmulas de Vieta

Las fórmulas de Vieta (nombradas en honor a François Viète ) son las relaciones entre las raíces de un polinomio cuadrático y sus coeficientes. Son el resultado de comparar término por término la relación con la ecuación $${\displaystyle x_{1}+x_{2}=-{\frac {b}{a}},\quad x_{1}x_{2}={\frac {c}{a}}}$$ $${\displaystyle \left(x-x_{1}\right)\left(x-x_{2}\right)=x^{2}-\left(x_{1}+x_{2}\right)x+x_{1}x_{2}=0}$$ $${\displaystyle x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0.}$$

La primera fórmula de Vieta es útil para graficar una función cuadrática. Dado que el gráfico es simétrico con respecto a una línea vertical que pasa por el vértice , la coordenada x del vértice se ubica en el promedio de las raíces (o intersecciones). Por lo tanto, la coordenada x del vértice es La coordenada y se puede obtener sustituyendo el resultado anterior en la ecuación cuadrática dada, lo que da Además, estas fórmulas para el vértice se pueden deducir directamente de la fórmula (ver Completar el cuadrado ) $${\displaystyle x_{V}={\frac {x_{1}+x_{2}}{2}}=-{\frac {b}{2a}}.}$$ $${\displaystyle y_{V}=-{\frac {b^{2}}{4a}}+c=-{\frac {b^{2}-4ac}{4a}}.}$$ $${\displaystyle ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}-4ac}{4a}}.}$$

Para el cálculo numérico, las fórmulas de Vieta proporcionan un método útil para hallar las raíces de una ecuación cuadrática en el caso en que una raíz sea mucho más pequeña que la otra. Si | x ₂ | << | x ₁ | , entonces x ₁ + x ₂ ≈ x ₁ , y tenemos la estimación: La segunda fórmula de Vieta proporciona entonces: Estas fórmulas son mucho más fáciles de evaluar que la fórmula cuadrática bajo la condición de una raíz grande y una pequeña, porque la fórmula cuadrática evalúa la raíz pequeña como la diferencia de dos números casi iguales (el caso de b grande ), lo que causa un error de redondeo en una evaluación numérica. La figura muestra la diferencia entre ^{[ aclaración necesaria ]} (i) una evaluación directa utilizando la fórmula cuadrática (precisa cuando las raíces están cerca una de la otra en valor) y (ii) una evaluación basada en la aproximación anterior de las fórmulas de Vieta (precisa cuando las raíces están ampliamente espaciadas). A medida que aumenta el coeficiente lineal b , la fórmula cuadrática es precisa al principio y la fórmula aproximada mejora en precisión, lo que lleva a una diferencia menor entre los métodos a medida que aumenta b . Sin embargo, en algún momento la fórmula cuadrática comienza a perder precisión debido al error de redondeo, mientras que el método aproximado continúa mejorando. En consecuencia, la diferencia entre los métodos comienza a aumentar a medida que la fórmula cuadrática empeora cada vez más. $${\displaystyle x_{1}\approx -{\frac {b}{a}}.}$$ $${\displaystyle x_{2}={\frac {c}{ax_{1}}}\approx -{\frac {c}{b}}.}$$

Esta situación surge comúnmente en el diseño de amplificadores, donde se desean raíces ampliamente separadas para garantizar una operación estable (ver Respuesta al escalón ).

Solución trigonométrica

En la época anterior a las calculadoras, la gente utilizaba tablas matemáticas (listas de números que mostraban los resultados de un cálculo con distintos argumentos) para simplificar y acelerar los cálculos. Las tablas de logaritmos y funciones trigonométricas eran habituales en los libros de texto de matemáticas y ciencias. Se publicaron tablas especializadas para aplicaciones como la astronomía, la navegación celeste y la estadística. Existían métodos de aproximación numérica, llamados prostaféresis , que ofrecían atajos para operaciones que consumían mucho tiempo, como la multiplicación y la extracción de potencias y raíces. ^[35] Los astrónomos, en particular, estaban interesados ​​en métodos que pudieran acelerar las largas series de cálculos implicados en los cálculos de mecánica celeste .

Es en este contexto que podemos entender el desarrollo de medios para resolver ecuaciones cuadráticas con la ayuda de la sustitución trigonométrica . Consideremos la siguiente forma alternativa de la ecuación cuadrática,

donde el signo del símbolo ± se elige de modo que a y c sean ambos positivos. Sustituyendo

y luego multiplicando por cos ² ( θ ) / c , obtenemos

Introduciendo funciones de 2 θ y reordenando, obtenemos

donde los subíndices n y p corresponden, respectivamente, al uso de un signo negativo o positivo en la ecuación [1] . Sustituyendo los dos valores de θ _n o θ _p encontrados a partir de las ecuaciones [4] o [5] en [2] se obtienen las raíces requeridas de [1] . Las raíces complejas ocurren en la solución basada en la ecuación [5] si el valor absoluto de sen 2 θ _p excede la unidad. La cantidad de esfuerzo involucrado en la resolución de ecuaciones cuadráticas utilizando esta estrategia mixta de búsqueda de tablas trigonométricas y logarítmicas fue dos tercios del esfuerzo utilizando solo tablas logarítmicas. ^[36] Calcular raíces complejas requeriría utilizar una forma trigonométrica diferente. ^[37]

Para ilustrarlo, supongamos que disponemos de tablas trigonométricas y logarítmicas de siete cifras y deseamos resolver lo siguiente con una precisión de seis cifras significativas: $${\displaystyle 4.16130x^{2}+9.15933x-11.4207=0}$$

1. Una tabla de búsqueda de siete lugares podría tener solo 100.000 entradas, y el cálculo de resultados intermedios hasta siete lugares generalmente requeriría una interpolación entre entradas adyacentes.
2. ${\displaystyle \log a=0.6192290,\log b=0.9618637,\log c=1.0576927}$
3. ${\displaystyle 2{\sqrt {ac}}/b=2\times 10^{(0.6192290+1.0576927)/2-0.9618637}=1.505314}$
4. ${\displaystyle \theta =(\tan ^{-1}1.505314)/2=28.20169^{\circ }{\text{ or }}-61.79831^{\circ }}$
5. ${\displaystyle \log |\tan \theta |=-0.2706462{\text{ or }}0.2706462}$
6. ${\displaystyle \log {\textstyle {\sqrt {c/a}}}=(1.0576927-0.6192290)/2=0.2192318}$
7. ${\displaystyle x_{1}=10^{0.2192318-0.2706462}=0.888353}$(redondeado a seis cifras significativas) $${\displaystyle x_{2}=-10^{0.2192318+0.2706462}=-3.08943}$$

Solución para raíces complejas en coordenadas polares

Si la ecuación cuadrática con coeficientes reales tiene dos raíces complejas (el caso en el que se requiere que a y c tengan el mismo signo entre sí), entonces las soluciones para las raíces se pueden expresar en forma polar como ^[38] ${\displaystyle ax^{2}+bx+c=0}$ ${\displaystyle b^{2}-4ac<0,}$

$${\displaystyle x_{1},\,x_{2}=r(\cos \theta \pm i\sin \theta ),}$$

donde y ${\displaystyle r={\sqrt {\tfrac {c}{a}}}}$ ${\displaystyle \theta =\cos ^{-1}\left({\tfrac {-b}{2{\sqrt {ac}}}}\right).}$

Solución geométrica

Figura 6. Solución geométrica de ax ² + bx + c = 0 utilizando el método de Lill. Las soluciones son −AX1/SA, −AX2/SA

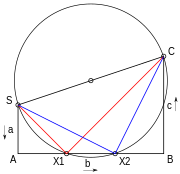
La ecuación cuadrática se puede resolver geométricamente de varias maneras. Una de ellas es mediante el método de Lill . Los tres coeficientes a , b , c se dibujan formando ángulos rectos entre ellos, como en SA, AB y BC en la Figura 6. Se dibuja un círculo con el punto inicial y final SC como diámetro. Si este corta la línea media AB de las tres, entonces la ecuación tiene una solución, y las soluciones se dan por el negativo de la distancia a lo largo de esta línea desde A dividido por el primer coeficiente a o SA. Si a es 1, los coeficientes se pueden leer directamente. Por lo tanto, las soluciones en el diagrama son −AX1/SA y −AX2/SA. ^[39]

Círculo de Carlyle de la ecuación cuadrática x ²  −  sx  +  p  = 0.

El círculo de Carlyle , llamado así en honor a Thomas Carlyle , tiene la propiedad de que las soluciones de la ecuación cuadrática son las coordenadas horizontales de las intersecciones del círculo con el eje horizontal . ^[40] Los círculos de Carlyle se han utilizado para desarrollar construcciones con regla y compás de polígonos regulares .

Generalización de la ecuación cuadrática

La fórmula y su derivación siguen siendo correctas si los coeficientes a , b y c son números complejos o, más generalmente, miembros de cualquier cuerpo cuya característica no sea 2. (En un cuerpo de característica 2, el elemento 2 a es cero y es imposible dividirlo por él).

El símbolo en la fórmula debe entenderse como "cualquiera de los dos elementos cuyo cuadrado es b ² − 4 ac , si tales elementos existen". En algunos campos, algunos elementos no tienen raíces cuadradas y otros tienen dos; solo el cero tiene una sola raíz cuadrada, excepto en campos de característica 2 . Incluso si un campo no contiene una raíz cuadrada de algún número, siempre hay un campo de extensión cuadrático que sí la contiene, por lo que la fórmula cuadrática siempre tendrá sentido como fórmula en ese campo de extensión. $${\displaystyle \pm {\sqrt {b^{2}-4ac}}}$$

Característica 2

En un cuerpo de característica 2 , la fórmula cuadrática, que se basa en que 2 es una unidad , no se cumple. Considere el polinomio cuadrático mónico sobre un cuerpo de característica 2 . Si b = 0 , entonces la solución se reduce a extraer una raíz cuadrada, por lo que la solución es y solo hay una raíz ya que En resumen, consulte residuo cuadrático para obtener más información sobre la extracción de raíces cuadradas en cuerpos finitos. $${\displaystyle x^{2}+bx+c}$$ $${\displaystyle x={\sqrt {c}}}$$ $${\displaystyle -{\sqrt {c}}=-{\sqrt {c}}+2{\sqrt {c}}={\sqrt {c}}.}$$ $${\displaystyle \displaystyle x^{2}+c=(x+{\sqrt {c}})^{2}.}$$

En el caso de que b ≠ 0 , hay dos raíces distintas, pero si el polinomio es irreducible , no se pueden expresar en términos de raíces cuadradas de números en el cuerpo de coeficientes. En cambio, defina la raíz 2 R ( c ) de c como una raíz del polinomio x ² + x + c , un elemento del cuerpo de descomposición de ese polinomio. Se verifica que R ( c ) + 1 también es una raíz. En términos de la operación de raíz 2, las dos raíces del polinomio cuadrático (no mónico) ax ² + bx + c son y $${\displaystyle {\frac {b}{a}}R\left({\frac {ac}{b^{2}}}\right)}$$ $${\displaystyle {\frac {b}{a}}\left(R\left({\frac {ac}{b^{2}}}\right)+1\right).}$$

Por ejemplo, sea a un generador multiplicativo del grupo de unidades de F ₄ , el campo de Galois de orden cuatro (por lo tanto a y a + 1 son raíces de x ² + x + 1 sobre F ₄ . Como ( a + 1) ² = a , a + 1 es la única solución de la ecuación cuadrática x ² + a = 0 . Por otra parte, el polinomio x ² + ax + 1 es irreducible sobre F ₄ , pero se descompone sobre F ₁₆ , donde tiene las dos raíces ab y ab + a , donde b es una raíz de x ² + x + a en F ₁₆ .

Éste es un caso especial de la teoría de Artin-Schreier .

Véase también

• Resolver ecuaciones cuadráticas con fracciones continuas
• Ecuación lineal
• Función cúbica
• Ecuación cuártica
• Ecuación quíntica
• Teorema fundamental del álgebra

Referencias

1. Charles P. McKeague (2014). Álgebra intermedia con trigonometría (edición reimpresa). Academic Press. pág. 219. ISBN 978-1-4832-1875-5.Extracto de la página 219
2. Protters & Morrey: "Cálculo y geometría analítica. Primer curso".
3. The Princeton Review (2020). Preparación para el examen SAT de Princeton Review, 2021: 5 exámenes de práctica + repaso y técnicas + herramientas en línea. Random House Children's Books. pág. 360. ISBN 978-0-525-56974-9.Extracto de la página 360
4. David Mumford; Caroline Series; David Wright (2002). Las perlas de Indra: la visión de Felix Klein (edición ilustrada y reimpresa). Cambridge University Press. pág. 37. ISBN 978-0-521-35253-6.Extracto de la página 37
5. Matemáticas en acción, libro de recursos para docentes 4b (edición ilustrada). Nelson Thornes. 1996. pág. 26. ISBN 978-0-17-431439-4.Extracto de la página 26
6. Washington, Allyn J. (2000). Matemáticas técnicas básicas con cálculo, séptima edición . Addison Wesley Longman, Inc. ISBN 978-0-201-35666-3.
7. Ebbinghaus, Heinz-Dieter; Ewing, John H. (1991), Números, Textos de posgrado en matemáticas, vol. 123, Springer, pág. 77, ISBN 9780387974972.
8. Sterling, Mary Jane (2010), Álgebra I para tontos, Wiley Publishing, pág. 219, ISBN 978-0-470-55964-2
9. Rich, Barnett; Schmidt, Philip (2004), Esquema de teoría y problemas de álgebra elemental de Schaum, The McGraw-Hill Companies, ISBN 978-0-07-141083-0, Capítulo 13 §4.4, pág. 291
10. Himonas, Alex. Cálculo para empresas y ciencias sociales , pág. 64 (Richard Dennis Publications, 2001).
11. Kahan, Willian (20 de noviembre de 2004), Sobre el costo del cálculo de punto flotante sin aritmética extraprecisa (PDF) , consultado el 25 de diciembre de 2012
12. Alenit͡syn, Aleksandr y Butikov, Evgeniĭ. Manual conciso de matemáticas y física , pág. 38 (CRC Press 1997)
13. Δ es la inicial de la palabra griega Δ ιακρίνουσα, Diakrínousa , discriminante.
14. Achatz, Thomas; Anderson, John G.; McKenzie, Kathleen (2005). Matemáticas de taller técnico. Prensa industrial. pág. 277. ISBN 978-0-8311-3086-2.
15. "Raíces complejas hechas visibles: datos curiosos sobre matemáticas" . Consultado el 1 de octubre de 2016 .
16. Wharton, P. (2006). Fundamentos de Edexcel Gcse Math/Higher. Lonsdale. pág. 63. ISBN 978-1-905-129-78-2.
17. Alec Norton, Benjamin Lotto (junio de 1984), "Raíces complejas hechas visibles", The College Mathematics Journal , 15 (3): 248–249, doi :10.2307/2686333, JSTOR  2686333
18. Higham, Nicholas (2002), Precisión y estabilidad de algoritmos numéricos (2.ª ed.), SIAM, pág. 10, ISBN 978-0-89871-521-7
19. Friberg, Jöran (2009). "Un algoritmo geométrico con soluciones a ecuaciones cuadráticas en un documento jurídico sumerio de Ur III Umma". Revista Cuneiforme de la Biblioteca Digital . 3 .
20. Stillwell, John (2004). Matemáticas y su historia (2.ª ed.) . Springer. ISBN 978-0-387-95336-6.
21. La historia antigua de Cambridge, parte 2. Historia temprana de Oriente Medio. Cambridge University Press. 1971. pág. 530. ISBN 978-0-521-07791-0.
22. Henderson, David W. "Soluciones geométricas de ecuaciones cuadráticas y cúbicas". Departamento de Matemáticas, Universidad de Cornell . Consultado el 28 de abril de 2013 .
23. Aitken, Wayne. "Un clásico chino: los nueve capítulos" (PDF) . Departamento de Matemáticas, Universidad Estatal de California . Consultado el 28 de abril de 2013 .
24. Smith, David Eugene (1958). Historia de las matemáticas. Courier Dover Publications. pág. 380. ISBN 978-0-486-20430-7.
25. Smith, David Eugene (1958). Historia de las matemáticas, volumen 1. Courier Dover Publications. pág. 134. ISBN 978-0-486-20429-1.Extracto de la página 134
26. Brāhmasphuṭasiddhānta, traducción de Colebrook, 1817, página 346; citado por Stillwell, John (2010). Matemáticas y su historia (3.ª ed.) . Springer. pág. 93. doi :10.1007/978-1-4419-6053-5. ISBN 978-0-387-95336-6.
27. Katz, VJ; Barton, B. (2006). "Etapas en la historia del álgebra con implicaciones para la enseñanza". Estudios educativos en matemáticas . 66 (2): 185–201. doi :10.1007/s10649-006-9023-7. S2CID  120363574.
28. Boyer, Carl B. (1991). Merzbach, Uta C. (ed.). Una historia de las matemáticas. John Wiley & Sons, Inc. ISBN 978-0-471-54397-8.
29. O'Connor, John J.; Robertson, Edmund F. (1999), "Matemáticas árabes: ¿brillantez olvidada?", Archivo de Historia de las Matemáticas MacTutor , Universidad de St Andrews"El álgebra era una teoría unificadora que permitía que los números racionales, los números irracionales, las magnitudes geométricas, etc., fueran tratados como "objetos algebraicos"."
30. Jacques Sesiano, "Matemáticas islámicas", p. 148, en Selin, Helaine ; D'Ambrosio, Ubiratan , eds. (2000), Matemáticas entre culturas: la historia de las matemáticas no occidentales , Springer , ISBN 978-1-4020-0260-1
31. Smith, David Eugene (1958). Historia de las matemáticas. Courier Dover Publications. pág. 280. ISBN 978-0-486-20429-1.
32. Livio, Mario (2006). La ecuación que no se pudo resolver. Simon & Schuster. ISBN 978-0743258210.
33. Ronan, Colin (1985). La ciencia y la civilización en China. Cambridge University Press. pág. 15. ISBN 978-0-521-31536-4.
34. Struik, DJ; Stevin, Simon (1958), Las principales obras de Simon Stevin, Matemáticas (PDF) , vol. II–B, CV Swets & Zeitlinger, pág. 470
35. Ballew, Pat. "Resolución de ecuaciones cuadráticas mediante métodos analíticos y gráficos; incluidos varios métodos que quizás nunca haya visto" (PDF) . Archivado desde el original (PDF) el 9 de abril de 2011. Consultado el 18 de abril de 2013 .
36. Seares, FH (1945). "Solución trigonométrica de la ecuación cuadrática". Publicaciones de la Sociedad Astronómica del Pacífico . 57 (339): 307–309. Bibcode :1945PASP...57..307S. doi : 10.1086/125759 .
37. Aude, HTR (1938). "Las soluciones de la ecuación cuadrática obtenidas con la ayuda de la trigonometría". Revista Nacional de Matemáticas . 13 (3): 118–121. doi :10.2307/3028750. JSTOR  3028750.
38. Simons, Stuart, "Enfoque alternativo a raíces complejas de ecuaciones cuadráticas reales", Mathematical Gazette 93, marzo de 2009, 91–92.
39. Bixby, William Herbert (1879), Método gráfico para encontrar fácilmente las raíces reales de ecuaciones numéricas de cualquier grado , West Point NY
40. Weisstein, Eric W. "Carlyle Circle". De MathWorld—A Wolfram Web Resource . Consultado el 21 de mayo de 2013 .

Enlaces externos

• "Ecuación cuadrática", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Ecuaciones cuadráticas". MathWorld .
• 101 usos de una ecuación cuadrática Archivado el 10 de noviembre de 2007 en Wayback Machine
• 101 usos de una ecuación cuadrática: Parte II Archivado el 22 de octubre de 2007 en Wayback Machine