0,999...

Alternative decimal expansion of 1

Impresión estilística del número, que representa cómo sus decimales continúan infinitamente.

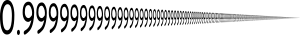
En matemáticas , 0,999... (también escrito como 0, 9 , 0..9o 0.(9) ) es una notación para el decimal periódico que consiste en una secuencia interminable de 9 después del punto decimal . Este decimal periódico es un número que representa el número más pequeño, nada menos que cada número de la secuencia (0,9, 0,99, 0,999,...); es decir, el supremo de esta secuencia. ^[1] Este número es igual a  1. En otras palabras, "0,999..." no es "casi exactamente" o "muy, muy cerca pero no del todo" 1  , sino "0,999..." y "1". representan exactamente el mismo número.

Hay muchas maneras de mostrar esta igualdad, desde argumentos intuitivos hasta demostraciones matemáticamente rigurosas . La técnica utilizada depende del público objetivo, los supuestos de fondo, el contexto histórico y el desarrollo preferido de los números reales , el sistema dentro del cual 0,999... se define comúnmente. En otros sistemas, 0,999... puede tener el mismo significado, una definición diferente o no estar definido.

De manera más general, cada decimal terminado en distinto de cero tiene dos representaciones iguales (por ejemplo, 8,32 y 8,31999...), lo cual es una propiedad de todas las representaciones de sistemas numéricos posicionales independientemente de su base . La preferencia utilitaria por la representación decimal terminal contribuye a la idea errónea de que es la única representación. Por esta y otras razones (como pruebas rigurosas que se basan en técnicas, propiedades o disciplinas no elementales) algunas personas pueden encontrar la igualdad lo suficientemente contraintuitiva como para cuestionarla o rechazarla. Este ha sido objeto de varios estudios en educación matemática .

Prueba elemental

La propiedad de Arquímedes : cualquier punto x antes de la línea de meta se encuentra entre dos de los puntos (inclusive). ${\displaystyle P_{n}}$

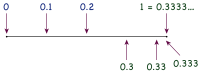
Existe una prueba elemental de la ecuación 0,999... = 1 , que utiliza sólo las herramientas matemáticas de comparación y suma de números decimales (finitos) , sin ninguna referencia a temas más avanzados como series , límites , construcción formal de números reales. , etc. La prueba que se presenta a continuación ^[2] es una formalización directa del hecho intuitivo de que, si se dibuja 0,9, 0,99, 0,999, etc. en la recta numérica , no queda espacio para colocar un número entre ellos y 1. El significado de la notación 0,999... es el punto menor en la recta numérica que se encuentra a la derecha de todos los números 0,9, 0,99, 0,999, etc. Debido a que, en última instancia, no hay espacio entre el 1 y estos números, el punto 1 debe ser este punto mínimo, por lo que 0,999... = 1 .

Explicación intuitiva

Si uno coloca 0,9, 0,99, 0,999, etc. en la recta numérica , ve inmediatamente que todos estos puntos están a la izquierda de 1, y que se acercan cada vez más a 1.

Más precisamente, la distancia de 0,9 a 1 es 0,1 = 1/10 , la distancia de 0,99 a 1 es 0,01 = 1/10 ² , y así sucesivamente. La distancia a 1 desde el enésimo punto (el que tiene n 9 después del punto decimal) es 1/10 ⁿ .

Por lo tanto, si 1 no fuera el número más pequeño mayor que 0,9, 0,99, 0,999, etc., entonces habría un punto en la recta numérica que se encuentra entre 1 y todos estos puntos. Este punto estaría a una distancia positiva de 1 que es menor que 1/10 ⁿ por cada número entero n . En los sistemas numéricos estándar (los números racionales y los números reales ), no hay ningún número positivo que sea menor que 1/10 ⁿ para todo n . Esta es (una versión de) la propiedad de Arquímedes , que se puede demostrar que se cumple en el sistema de números racionales. Por lo tanto, 1 es el número más pequeño que es mayor que todos los 0,9, 0,99, 0,999, etc., por lo que 1 = 0,999... .

Discusión sobre la integridad

Parte de lo que muestra este argumento es que existe un límite superior mínimo de la secuencia 0,9, 0,99, 0,999, etc.: el número más pequeño que es mayor que todos los términos de la secuencia. Uno de los axiomas del sistema de números reales es el axioma de completitud , que establece que toda secuencia acotada tiene un límite superior mínimo. Este límite superior mínimo es una forma de definir expansiones decimales infinitas: el número real representado por un decimal infinito es el límite superior mínimo de sus truncamientos finitos. El argumento aquí no necesita asumir que la integridad es válida, porque muestra que esta secuencia particular de números racionales tiene un límite superior mínimo y que este límite superior mínimo es igual a uno.

Prueba rigurosa

La explicación anterior no es una prueba, ya que no se puede definir adecuadamente la relación entre un número y su representación como un punto en la recta numérica. Para la exactitud de la prueba, el número 0,999...9 , con n nueves después del punto decimal, se denota 0.(9) _n . Por lo tanto, 0.(9) ₁ = 0.9 , 0.(9) ₂ = 0.99 , 0.(9) ₃ = 0.999 , y así sucesivamente. Como 1/10 ⁿ = 0.0...01 , con n dígitos después del punto decimal, la regla de la suma para números decimales implica

${\displaystyle 0.(9)_{n}+1/10^{n}=1,}$

y

${\displaystyle 0.(9)_{n}<1,}$

para cada entero positivo n .

Hay que demostrar que 1 es el número más pequeño que no es menor que todos los 0.(9) _n . Para ello basta demostrar que, si un número x no es mayor que 1 ni menor que todos los 0.(9) _n , entonces x = 1 . Entonces sea x tal que

${\displaystyle 0.(9)_{n}\leq x\leq 1,}$

para cada entero positivo n . Por lo tanto,

${\displaystyle 1-1\leq 1-x\leq 1-0.(9)_{n}.}$

que, utilizando aritmética básica y la primera igualdad establecida anteriormente, se simplifica a

${\displaystyle 0\leq 1-x\leq 1/10^{n}.}$

Esto implica que la diferencia entre 1 y x es menor que la inversa de cualquier número entero positivo. Por tanto, esta diferencia debe ser cero y, por tanto, x = 1 ; eso es

${\displaystyle 0.999\ldots =1.}$

Esta prueba se basa en el hecho de que cero es el único número no negativo que es menor que todos los inversos de los números enteros o, de manera equivalente, que no hay ningún número que sea mayor que todos los números enteros. Esta es la propiedad de Arquímedes , que se verifica para números racionales y números reales . Los números reales pueden ampliarse a sistemas numéricos , como los números hiperreales , con números infinitamente pequeños ( infinitésimos ) y números infinitamente grandes ( números infinitos ). Cuando se utilizan tales sistemas, generalmente no se usa la notación 0,999..., ya que no hay ningún número más pequeño que no sea menor que todo 0.(9) _n . (Esto está implícito en el hecho de que 0.(9) _n ≤ x < 1 implica 0.(9) _{n –1} ≤ 2 x – 1 < x < 1 ).

argumentos algebraicos

Se han proporcionado muchos argumentos algebraicos que sugieren que no son pruebas matemáticas , ya que normalmente se basan en el hecho de que las reglas para sumar y multiplicar decimales finitos se extienden a decimales infinitos. Esto es cierto, pero la prueba es esencialmente la misma que la prueba de Entonces, todos estos argumentos son esencialmente razonamientos circulares . ${\displaystyle 1=0.999\ldots }$ ${\displaystyle 1=0.999\ldots }$

Sin embargo, la cuestión de las ilustraciones demasiado simplificadas de la igualdad es un tema de discusión y crítica pedagógica. Byers (2007, p. 39) analiza el argumento de que, en la escuela primaria, se enseña que 1 ⁄ 3 = 0,333... , por lo que, ignorando todas las sutilezas esenciales, "multiplicar" esta identidad por 3 da 1=0,999. . . Dice además que este argumento no es convincente debido a una ambigüedad no resuelta sobre el significado del signo igual ; un estudiante podría pensar: "Seguramente no significa que el número 1 sea idéntico al significado de la notación 0,999... ". La mayoría de los estudiantes universitarios de matemáticas con los que se encontró Byers sienten que, si bien 0,999... es "muy cercano" a 1 según la solidez de este argumento, y algunos incluso dicen que es "infinitamente cercano", no están preparados para decir que es igual. a 1. Richman (1999) analiza cómo "este argumento obtiene su fuerza del hecho de que la mayoría de las personas han sido adoctrinadas para aceptar la primera ecuación sin pensar", pero también sugiere que el argumento puede llevar a los escépticos a cuestionar esta suposición.

Byers también presenta el siguiente argumento.

${\displaystyle {\begin{aligned}x&=0.999\ldots \\10x&=9.999\ldots &&{\text{by multiplying by }}10\\10x&=9+0.999\ldots &&{\text{by splitting off integer part}}\\10x&=9+x&&{\text{by definition of }}x\\9x&=9&&{\text{by subtracting }}x\\x&=1&&{\text{by dividing by }}9\end{aligned}}}$

Los estudiantes que no aceptaron el primer argumento a veces aceptan el segundo argumento, pero, en opinión de Byers, todavía no han resuelto la ambigüedad y, por lo tanto, no comprenden la representación de infinitos decimales. Peressini y Peressini (2007), presentando el mismo argumento, también afirman que no explica la igualdad, indicando que tal explicación probablemente involucraría conceptos de infinito y completitud . ^[3] Baldwin & Norton (2012), citando a Katz & Katz (2010a), también concluyen que el tratamiento de la identidad basado en argumentos como estos, sin el concepto formal de límite, es prematuro. ^[4]

Richman (1999) también presenta el mismo argumento, quien señala que los escépticos pueden cuestionar si x es cancelable  , es decir, si tiene sentido restar x de ambos lados.

Pruebas analíticas

Dado que la cuestión de 0,999... no afecta el desarrollo formal de las matemáticas, puede posponerse hasta que se demuestren los teoremas estándar del análisis real . Un requisito es caracterizar los números reales que se pueden escribir en notación decimal, que consisten en un signo opcional, una secuencia finita de uno o más dígitos que forman una parte entera, un separador decimal y una secuencia de dígitos que forman una parte fraccionaria. A los efectos de analizar 0,999..., la parte entera se puede resumir como b ₀ y se pueden despreciar los negativos, por lo que una expansión decimal tiene la forma

$${\displaystyle b_{0}.b_{1}b_{2}b_{3}b_{4}b_{5}\dots .}$$

La parte fraccionaria, a diferencia de la parte entera, no se limita a un número finito de dígitos. Esta es una notación posicional , así por ejemplo el dígito 5 en 500 aporta diez veces más que el 5 en 50, y el 5 en 0,05 aporta una décima parte que el 5 en 0,5.

Series y secuencias infinitas

Un desarrollo común de las expansiones decimales es definirlas como sumas de series infinitas . En general:

$${\displaystyle b_{0}.b_{1}b_{2}b_{3}b_{4}\ldots =b_{0}+b_{1}\left({\tfrac {1}{10}}\right)+b_{2}\left({\tfrac {1}{10}}\right)^{2}+b_{3}\left({\tfrac {1}{10}}\right)^{3}+b_{4}\left({\tfrac {1}{10}}\right)^{4}+\cdots .}$$

Para 0,999... se puede aplicar el teorema de convergencia relativo a las series geométricas , afirmando que si , entonces: ^[5] ${\displaystyle |r|<1}$

$${\displaystyle ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}.}$$

Dado que 0,999... es una suma con a = 9 y una razón común r = 1 ⁄ 10 , el teorema resuelve rápidamente la pregunta:

$${\displaystyle 0.999\ldots =9\left({\tfrac {1}{10}}\right)+9\left({\tfrac {1}{10}}\right)^{2}+9\left({\tfrac {1}{10}}\right)^{3}+\cdots ={\frac {9\left({\tfrac {1}{10}}\right)}{1-{\tfrac {1}{10}}}}=1.}$$

Elementos de álgebraLeonhard Euler^[6]

Límites: el intervalo unitario, incluida la secuencia de fracciones de base 4 (.3, .33, .333, ...) que converge a 1.

La suma de una serie geométrica es en sí misma un resultado incluso más antiguo que Euler. Una derivación típica del siglo XVIII utilizó una manipulación término por término similar a la prueba algebraica dada anteriormente, y aún en 1811, el libro de texto de Bonnycastle Introducción al álgebra utiliza dicho argumento para series geométricas para justificar la misma maniobra en 0,999. ^[7] Una reacción del siglo XIX contra estos métodos liberales de suma resultó en la definición que todavía domina hoy: la suma de una serie se define como el límite de la secuencia de sus sumas parciales. Una prueba correspondiente del teorema calcula explícitamente esa secuencia; se puede encontrar en cualquier introducción al cálculo o análisis basada en pruebas. ^[8]

Una secuencia ( x ₀ , x ₁ , x ₂ , ...) tiene el valor x como límite si la distancia | x - x _norte | se vuelve arbitrariamente pequeño a medida que n aumenta. La afirmación de que 0,999... = 1 puede interpretarse y demostrarse como un límite: ^[9]

$${\displaystyle 0.999\ldots \ {\overset {\underset {\mathrm {def} }{}}{=}}\ \lim _{n\to \infty }0.\underbrace {99\ldots 9} _{n}\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1-0=1.}$$

1 ⁄ 10 ⁿ → 0n → ∞propiedad de Arquímedes0,999...The University ArithmeticAritmética para Escuelas^[10]heurísticas en el sentido de que implican que 0,999...

Intervalos anidados y límites superiores mínimos

Intervalos anidados: en base 3, 1 = 1.000... = 0.222...

La definición de serie anterior es una forma sencilla de definir el número real denominado mediante una expansión decimal. Un enfoque complementario se adapta al proceso opuesto: para un número real dado, defina las expansiones decimales para nombrarlo.

Si se sabe que un número real x se encuentra en el intervalo cerrado [0, 10] (es decir, es mayor o igual a 0 y menor o igual a 10), uno puede imaginar dividir ese intervalo en diez partes que se superponen. sólo en sus puntos finales: [0, 1], [1, 2], [2, 3], y así sucesivamente hasta [9, 10]. El número x debe pertenecer a uno de estos; si pertenece a [2, 3], entonces se registra el dígito "2" y se subdivide ese intervalo en [2, 2.1], [2.1, 2.2], ..., [2.8, 2.9], [2.9, 3] . Continuar con este proceso produce una secuencia infinita de intervalos anidados , etiquetados por una secuencia infinita de dígitos b ₀ , b ₁ , b ₂ , b ₃ , ... , y se escribe

$${\displaystyle x=b_{0}.b_{1}b_{2}b_{3}\ldots .}$$

En este formalismo, las identidades 1 = 0,999... y 1 = 1,000... reflejan, respectivamente, el hecho de que 1 se encuentra tanto en [0, 1] como en [1, 2], por lo que se puede elegir cualquiera de los subintervalos al encontrar sus dígitos. Para garantizar que esta notación no abuse del signo "=", se necesita una forma de reconstruir un número real único para cada decimal. Esto se puede hacer con límites, pero otras construcciones continúan con el tema ordenamiento. ^[11]

Una opción sencilla es el teorema de los intervalos anidados , que garantiza que dada una secuencia de intervalos cerrados anidados cuyas longitudes se vuelven arbitrariamente pequeñas, los intervalos contienen exactamente un número real en su intersección . Entonces b ₀ . b ₁ b ₂ b ₃ ... se define como el número único contenido dentro de todos los intervalos [ b ₀ , b ₀ + 1] , [ b ₀ . segundo ₁ , segundo ₀ . b ₁ + 0,1] , y así sucesivamente. 0,999... es entonces el único número real que se encuentra en todos los intervalos [0, 1], [0,9, 1], [0,99, 1] y [0,99...9, 1] para cada cadena finita de 9 chelines. Dado que 1 es un elemento de cada uno de estos intervalos, 0,999... = 1. ^[12]

El teorema de los intervalos anidados suele basarse en una característica más fundamental de los números reales: la existencia de límites superiores mínimos o suprema . Para explotar directamente estos objetos, se puede definir b ₀ . b ₁ b ₂ b ₃ ... ser el límite superior mínimo del conjunto de aproximantes { b ₀ , b ₀ . segundo ₁ , segundo ₀ . segundo ₁ segundo ₂ , ...}. ^[13] Entonces se puede demostrar que esta definición (o la definición de intervalos anidados) es consistente con el procedimiento de subdivisión, lo que implica 0,999... = 1 nuevamente. Tom Apostol concluye:

El hecho de que un número real pueda tener dos representaciones decimales diferentes es simplemente un reflejo del hecho de que dos conjuntos diferentes de números reales pueden tener el mismo supremo. ^[14]

Pruebas de la construcción de los números reales.

Algunos enfoques definen explícitamente los números reales como ciertas estructuras construidas sobre los números racionales , utilizando la teoría de conjuntos axiomática . Los números naturales  (0, 1, 2, 3, etc.) comienzan con 0 y continúan hacia arriba, de modo que cada número tiene un sucesor. Se pueden extender los números naturales con sus negativos para dar todos los números enteros y extenderlos aún más a razones, dando los números racionales . Estos sistemas numéricos van acompañados de la aritmética de suma, resta, multiplicación y división. De manera más sutil, incluyen el ordenamiento , de modo que se pueda comparar un número con otro y determinar que es menor, mayor o igual que otro número.

El paso de lo racional a lo real es una extensión importante. Hay al menos dos formas populares de lograr este paso, ambas publicadas en 1872: los cortes de Dedekind y las secuencias de Cauchy . Las pruebas de que 0,999... = 1 que utilizan directamente estas construcciones no se encuentran en los libros de texto sobre análisis real, donde la tendencia moderna de las últimas décadas ha sido utilizar un análisis axiomático. Incluso cuando se ofrece una construcción, generalmente se aplica para demostrar los axiomas de los números reales, que luego respaldan las demostraciones anteriores. Sin embargo, varios autores expresan la idea de que comenzar con una construcción es lógicamente más apropiado y las pruebas resultantes son más autónomas. ^[15]

cortes dedekind

En el método de corte de Dedekind , cada número real x se define como el conjunto infinito de todos los números racionales menores que x. ^[16] En particular, el número real 1 es el conjunto de todos los números racionales que son menores que 1. ^[17] Cada expansión decimal positiva determina fácilmente un corte de Dedekind: el conjunto de números racionales que son menores que alguna etapa de la expansión. . Entonces, el número real 0,999... es el conjunto de números racionales r tales que r < 0 , o r < 0,9 , o r < 0,99 , o r es menor que algún otro número de la forma ^[18]

$${\displaystyle 1-{\frac {1}{10^{n}}}=0.(9)_{n}=0.\underbrace {99\ldots 9} _{n{\text{ nines}}}.}$$

Cada elemento de 0,999... es menor que 1, por lo que es un elemento del número real 1. Por el contrario, todos los elementos de 1 son números racionales que se pueden escribir como

$${\displaystyle {\frac {a}{b}}<1,}$$

b > 0b > a

$${\displaystyle 1-{\frac {a}{b}}={\frac {b-a}{b}}\geq {\frac {1}{b}}>{\frac {1}{10^{b}}},}$$

$${\displaystyle {\frac {a}{b}}<1-{\frac {1}{10^{b}}}.}$$

Desde

$${\displaystyle 1-{\frac {1}{10^{b}}}=0.(9)_{b}<0.999\ldots ,}$$

La definición de números reales como cortes de Dedekind fue publicada por primera vez por Richard Dedekind en 1872. ^[19] El enfoque anterior para asignar un número real a cada expansión decimal se debe a un artículo expositivo titulado "¿Es 0,999... = 1?" por Fred Richman en Revista de Matemáticas . ^[20] Richman señala que tomar cortes de Dedekind en cualquier subconjunto denso de números racionales produce los mismos resultados; en particular, utiliza fracciones decimales , cuya demostración es más inmediata. También señala que normalmente las definiciones permiten que { x  : x < 1 } sea un corte pero no { x  : x ≤ 1 } (o viceversa): "¿Por qué hacer eso? Precisamente para descartar la existencia de números distintos 0,9* y 1. [...] Entonces vemos que en la definición tradicional de los números reales, la ecuación 0,9* = 1 está incorporada al principio." ^[21] Una modificación adicional del procedimiento conduce a una estructura diferente donde los dos no son iguales. Aunque es consistente, muchas de las reglas comunes de la aritmética decimal ya no se cumplen, por ejemplo la fracción 1 ⁄ 3 no tiene representación; consulte § Sistemas numéricos alternativos a continuación.

secuencias de cauchy

Otro enfoque consiste en definir un número real como el límite de una secuencia de Cauchy de números racionales. Esta construcción de los números reales utiliza el orden de los racionales de manera menos directa. Primero, la distancia entre xey se define como el valor absoluto | x − y | , donde el valor absoluto | z | se define como el máximo de z y − z , por lo que nunca es negativo. Entonces los reales se definen como las secuencias de racionales que tienen la propiedad de secuencia de Cauchy usando esta distancia. Es decir, en la secuencia ( x ₀ , x ₁ , x ₂ , ...) , una aplicación de números naturales a racionales, para cualquier δ racional positivo existe un N tal que | x _metro - x _norte | ≤ δ para todo metro , norte  >  norte . (La distancia entre términos se vuelve más pequeña que cualquier racional positivo). ^[22]

Si ( x _n ) y ( y _n ) son dos secuencias de Cauchy, entonces se definen como números reales iguales si la secuencia ( x _n  −  y _n ) tiene el límite 0. Truncamientos del número decimal b ₀ . b ₁ b ₂ b ₃ ... genera una secuencia de racionales que es Cauchy; esto se toma para definir el valor real del número. ^[23] Así, en este formalismo la tarea es mostrar que la secuencia de números racionales

$${\displaystyle \left(1-0,1-{9 \over 10},1-{99 \over 100},\dots \right)=\left(1,{1 \over 10},{1 \over 100},\dots \right)}$$

n- ${\displaystyle n\in \mathbb {N} }$

$${\displaystyle \lim _{n\rightarrow \infty }{\frac {1}{10^{n}}}=0.}$$

definición de límite^[24]

La definición de números reales como secuencias de Cauchy fue publicada por primera vez por separado por Eduard Heine y Georg Cantor , también en 1872. ^[19] El enfoque anterior para las expansiones decimales, incluida la prueba de que 0,999... = 1, sigue de cerca el de Griffiths y Hilton de 1970. trabajo Un libro de texto completo de matemáticas clásicas: una interpretación contemporánea . ^[25]

Representación decimal infinita

Comúnmente en la educación matemática de las escuelas secundarias , los números reales se construyen definiendo un número usando un número entero seguido de un punto de base y una secuencia infinita escrita como una cadena para representar la parte fraccionaria de cualquier número real dado. En esta construcción, el conjunto de cualquier combinación de un número entero y dígitos después del punto decimal (o punto de base en sistemas que no son de base 10) es el conjunto de números reales. Se puede demostrar rigurosamente que esta construcción satisface todos los axiomas reales después de definir una relación de equivalencia sobre el conjunto que define 1 = _eq 0,999... así como para cualquier otro decimal distinto de cero con sólo un número finito de términos distintos de cero en la cadena decimal con su Versión de 9 finales. ^[26] Con esta construcción de los reales, se puede considerar que todas las pruebas del enunciado "1 = 0,999..." suponen implícitamente la igualdad cuando se realizan operaciones con los números reales.

orden denso

Una de las nociones que puede resolver el problema es el requisito de que los números reales estén densamente ordenados. Los estudiantes dan por sentado que eso es antes , mientras que este tipo de orden intuitivo se define mejor como puramente lexicográfico. ${\displaystyle 0.99999...}$ ${\displaystyle 1}$

"... el orden de los números reales se reconoce como un orden denso. Sin embargo, dependiendo del contexto, los estudiantes pueden conciliar esta propiedad con la existencia de números justo antes o después de un número dado (0,999... así se ve a menudo como predecesor de 1)." ^[27]

El orden denso requiere que haya un tercer valor real estrictamente entre y , pero no lo hay: no podemos cambiar un solo dígito en ninguno de los dos para obtener tal número. Si y van a representar números reales, tienen que ser iguales. El orden denso implica que si no hay ningún elemento nuevo estrictamente entre dos elementos del conjunto, los dos elementos deben considerarse iguales. ${\displaystyle 0.99999...}$ ${\displaystyle 1}$ ${\displaystyle 0.99999...}$ ${\displaystyle 1}$

Generalizaciones

El resultado de que 0,999... = 1 se generaliza fácilmente de dos maneras. Primero, cada número distinto de cero con una notación decimal finita (equivalentemente, ceros finales interminables) tiene una contraparte con nueves finales. Por ejemplo, 0,24999... es igual a 0,25, exactamente como en el caso especial considerado. Estos números son exactamente fracciones decimales y son densos . ^[28]

En segundo lugar, se aplica un teorema comparable en cada base o base . Por ejemplo, en base 2 (el sistema de numeración binario ) 0,111... es igual a 1, y en base 3 (el sistema de numeración ternario ) 0,222... es igual a 1. En general, cualquier expresión terminal en base b tiene una contraparte con líneas finales repetidas. dígitos iguales a b − 1. Es probable que los libros de texto de análisis real se salten el ejemplo de 0,999... y presenten una o ambas generalizaciones desde el principio. ^[29]

Las representaciones alternativas de 1 también ocurren en bases no enteras. Por ejemplo, en la base de proporción áurea , las dos representaciones estándar son 1,000... y 0,101010..., y hay infinitas más representaciones que incluyen unos adyacentes. Generalmente, para casi todos los q entre 1 y 2, hay incontables expansiones de base q de 1. Por otro lado, todavía hay incontables q (incluidos todos los números naturales mayores que 1) para los cuales solo hay una base- q expansión de 1, distinta del trivial 1.000.... Este resultado fue obtenido por primera vez por Paul Erdős , Miklos Horváth e István Joó alrededor de 1990. En 1998, Vilmos Komornik y Paola Loreti determinaron la base más pequeña, la constante de Komornik-Loreti. q = 1,787231650.... En esta base, 1 = 0,11010011001011010010110011010011...; los dígitos vienen dados por la secuencia Thue-Morse , que no se repite. ^[30]

Una generalización de mayor alcance aborda los sistemas de numeración posicional más generales . Ellos también tienen múltiples representaciones y, en cierto sentido, las dificultades son aún peores. Por ejemplo: ^[31]

• En el sistema ternario equilibrado , 1 ⁄ 2 = 0,111... = 1,111 ....
• En el sistema numérico factorial inverso (usando bases 2!, 3!, 4!, ... para posiciones después del punto decimal), 1 = 1,000... = 0,1234....

Imposibilidad de representación única

El hecho de que todos estos diferentes sistemas numéricos adolezcan de representaciones múltiples para algunos números reales se puede atribuir a una diferencia fundamental entre los números reales como un conjunto ordenado y colecciones de cadenas infinitas de símbolos, ordenados lexicográficamente . De hecho, las dos propiedades siguientes explican la dificultad:

• Si un intervalo de números reales se divide en dos partes no vacías L , R , de modo que cada elemento de L es (estrictamente) menor que cada elemento de R , entonces L contiene un elemento más grande o R contiene un elemento más pequeño, pero no ambos.
• La colección de cadenas infinitas de símbolos tomadas de cualquier "alfabeto" finito, ordenadas lexicográficamente, se puede dividir en dos partes no vacías L , R , de modo que cada elemento de L es menor que cada elemento de R , mientras que L contiene el mayor. elemento y R contiene el elemento más pequeño. En efecto, basta con tomar dos prefijos finitos (subcadenas iniciales) p ₁ , p ₂ de elementos de la colección tales que difieren sólo en su símbolo final, para cuyo símbolo tienen valores sucesivos, y tomar por L el conjunto de todas las cadenas. en la colección cuyo prefijo correspondiente es como máximo p ₁ , y para R el resto, las cadenas de la colección cuyo prefijo correspondiente es al menos p ₂ . Entonces L tiene el elemento más grande, comenzando con p ₁ y eligiendo el símbolo más grande disponible en todas las posiciones siguientes, mientras que R tiene el elemento más pequeño obtenido siguiendo a p ₂ por el símbolo más pequeño en todas las posiciones.

El primer punto se deriva de las propiedades básicas de los números reales: L tiene un supremo y R tiene un mínimo , que se ve fácilmente que son iguales; al ser un número real, se encuentra en R o en L , pero no en ambos, ya que se supone que L y R son disjuntos . El segundo punto generaliza el par 0,999.../1,000... obtenido para p ₁  = "0", p ₂  = "1". De hecho, no es necesario utilizar el mismo alfabeto para todas las posiciones (de modo que, por ejemplo, se puedan incluir sistemas de bases mixtas ) ni considerar la colección completa de posibles cadenas; los únicos puntos importantes son que en cada posición se puede elegir un conjunto finito de símbolos (que incluso pueden depender de los símbolos anteriores) (esto es necesario para garantizar elecciones máximas y mínimas), y que hacer una elección válida para cualquier posición debe dar como resultado una cadena infinita válida (por lo que no se debe permitir "9" en cada posición y al mismo tiempo prohibir una sucesión infinita de "9"). Bajo estos supuestos, el argumento anterior muestra que un orden que preserva el mapa desde la colección de cadenas hasta un intervalo de números reales no puede ser una biyección : o algunos números no corresponden a ninguna cadena, o algunos de ellos corresponden a más de una cadena. .

Petkovšek (1990) ha demostrado que para cualquier sistema posicional que nombre todos los números reales, el conjunto de reales con múltiples representaciones es siempre denso. Él llama a la prueba "un ejercicio instructivo de topología elemental de conjuntos de puntos "; implica ver conjuntos de valores posicionales como espacios de piedra y notar que sus representaciones reales están dadas por funciones continuas . ^[32]

Aplicaciones

Una aplicación de 0,999... como representación de 1 ocurre en la teoría elemental de números . En 1802, H. Goodwin publicó una observación sobre la aparición de 9 en las representaciones decimales periódicas de fracciones cuyos denominadores son ciertos números primos . Ejemplos incluyen:

• 1 ⁄ 7 = 0, 142857 y 142 + 857 = 999.
• 1 ⁄ 73 = 0, 01369863 y 0136 + 9863 = 9999.

E. Midy demostró un resultado general sobre tales fracciones, ahora llamado teorema de Midy , en 1836. La publicación fue oscura y no está claro si su demostración involucraba directamente 0,999..., pero al menos una demostración moderna de WG Leavitt sí lo hace. Si se puede demostrar que si un decimal de la forma 0. b ₁ b ₂ b ₃ ... es un entero positivo, entonces debe ser 0,999..., que es entonces la fuente de los 9 en el teorema. ^[33] Las investigaciones en esta dirección pueden motivar conceptos como máximo común divisor , aritmética modular , primos de Fermat , orden de elementos de grupo y reciprocidad cuadrática . ^[34]

Posiciones de 1 ⁄ 4 , 2 ⁄ 3 y 1 en el conjunto de Cantor

Volviendo al análisis real, el análogo de base 3 0,222... = 1 juega un papel clave en la caracterización de uno de los fractales más simples, el conjunto de Cantor de tercios medios :

• Un punto en el intervalo unitario pertenece al conjunto de Cantor si y sólo si puede representarse en ternario utilizando sólo los dígitos 0 y 2.

El enésimo dígito de la representación refleja la posición del punto en la enésima etapa de la construcción. Por ejemplo, al punto 2 ⁄ 3 se le da la representación habitual de 0,2 o 0,2000..., ya que se encuentra a la derecha de la primera eliminación y a la izquierda de todas las eliminaciones posteriores. El punto 1 ⁄ 3 no se representa como 0,1 sino como 0,0222..., ya que se encuentra a la izquierda de la primera eliminación y a la derecha de todas las eliminaciones posteriores. ^[35]

La repetición de nueves también aparece en otra de las obras de Georg Cantor. Deben tenerse en cuenta para construir una prueba válida, aplicando su argumento diagonal de 1891 a las expansiones decimales, de la incontabilidad del intervalo unitario. Tal prueba debe poder declarar que ciertos pares de números reales son diferentes en función de sus expansiones decimales, por lo que es necesario evitar pares como 0,2 y 0,1999... Un método simple representa todos los números con expansiones no terminantes; el método opuesto descarta la repetición de nueves. ^[36] Una variante que puede estar más cerca del argumento original de Cantor usa la base 2, y al convertir expansiones de base 3 en expansiones de base 2, también se puede probar la incontabilidad del conjunto de Cantor. ^[37]

Escepticismo en la educación

Los estudiantes de matemáticas a menudo rechazan la igualdad de 0,999... y 1, por razones que van desde su apariencia dispar hasta profundos recelos sobre el concepto de límite y desacuerdos sobre la naturaleza de los infinitesimales . Hay muchos factores comunes que contribuyen a la confusión:

• Los estudiantes a menudo están "mentalmente comprometidos con la noción de que un número puede representarse de una y sólo una forma mediante un decimal". Ver dos decimales manifiestamente diferentes que representan el mismo número parece ser una paradoja , que se ve amplificada por la aparición del aparentemente bien entendido número 1. ^[38]
• Algunos estudiantes interpretan "0,999..." (o notación similar) como una cadena grande pero finita de 9, posiblemente con una longitud variable y no especificada. Si aceptan una cadena infinita de nueves, aún pueden esperar un último 9 "en el infinito". ^[39]
• La intuición y la enseñanza ambigua llevan a los estudiantes a pensar en el límite de una secuencia como una especie de proceso infinito en lugar de un valor fijo, ya que una secuencia no necesita alcanzar su límite. Cuando los estudiantes acepten la diferencia entre una secuencia de números y su límite, podrían leer "0,999..." en el sentido de la secuencia en lugar de su límite. ^[40]

Estas ideas son erróneas en el contexto de los números reales estándar, aunque algunas pueden ser válidas en otros sistemas numéricos, ya sea inventados por su utilidad matemática general o como contraejemplos instructivos para comprender mejor 0,999...

Muchas de estas explicaciones fueron encontradas por David Tall , quien estudió las características de la enseñanza y la cognición que llevaron a algunos de los malentendidos que encontró con sus estudiantes universitarios. Al entrevistar a sus estudiantes para determinar por qué la gran mayoría rechazaba inicialmente la igualdad, descubrió que "los estudiantes continuaron concibiendo 0,999... como una secuencia de números que se acercaban cada vez más a 1 y no como un valor fijo, porque 'no lo has hecho'. especificado cuántos lugares hay' o 'es el decimal más cercano posible debajo de 1 ' ". ^[41]

El argumento elemental de multiplicar 0,333... = 1 ⁄ 3 por 3 puede convencer a los estudiantes reacios de que 0,999... = 1. Aún así, cuando se enfrentan al conflicto entre su creencia en la primera ecuación y su incredulidad en la segunda, algunos estudiantes o comienza a no creer en la primera ecuación o simplemente se frustra. ^[42] Los métodos más sofisticados tampoco son infalibles: los estudiantes que son plenamente capaces de aplicar definiciones rigurosas pueden recurrir a imágenes intuitivas cuando se sorprenden con un resultado en matemáticas avanzadas, incluido 0,999.... Por ejemplo, un estudiante de análisis real pudo demostrar que 0,333... = 1 ⁄ 3 usando una definición suprema , pero luego insistió en que 0,999... < 1 basándose en su comprensión anterior de la división larga . ^[43] Otros todavía pueden probar que 1 ⁄ 3 = 0,333..., pero, al ser confrontados por la prueba fraccionaria, insisten en que la "lógica" reemplaza los cálculos matemáticos.

Mazur (2005) cuenta la historia de un brillante estudiante de cálculo que "cuestionó casi todo lo que dije en clase pero nunca cuestionó su calculadora", y que había llegado a creer que nueve dígitos es todo lo que uno necesita para hacer matemáticas, incluido el cálculo. la raíz cuadrada de 23. El estudiante se sintió incómodo con el argumento limitante de que 9,99... = 10, calificándolo de "un proceso de crecimiento infinito tremendamente imaginado". ^[44]

Como parte de la teoría APOS del aprendizaje matemático de Ed Dubinsky, él y sus colaboradores (2005) proponen que los estudiantes que conciben 0,999... como una cadena finita e indeterminada con una distancia infinitamente pequeña de 1 "aún no han construido una concepción de proceso completa". del decimal infinito". Otros estudiantes que tienen una concepción de proceso completa de 0.999... quizás aún no puedan "encapsular" ese proceso en una "concepción de objeto", como la concepción de objeto que tienen de 1, y por eso ven el proceso 0.999... y el objeto 1 como incompatible. Dubinsky y cols. También vincule esta capacidad mental de encapsulación con ver 1 ⁄ 3 como un número por derecho propio y con tratar el conjunto de números naturales como un todo. ^[45]

Fenómeno cultural

Con el auge de Internet , los debates sobre 0,999... se han convertido en algo común en los grupos de noticias y foros de mensajes , incluidos muchos que nominalmente tienen poco que ver con las matemáticas. En el grupo de noticias sci.math , discutir sobre 0,999... se describe como un "deporte popular" y es una de las preguntas respondidas en sus preguntas frecuentes . ^[46] Las preguntas frecuentes cubren brevemente 1 ⁄ 3 , la multiplicación por 10 y los límites, y también alude a las secuencias de Cauchy.

Una edición de 2003 de la columna del periódico de interés general The Straight Dope analiza 0,999... vía 1 ⁄ 3 y limita, diciendo sobre conceptos erróneos,

El primate inferior en nosotros todavía se resiste, diciendo: .999~ no representa realmente un número , sino un proceso . Para encontrar un número tenemos que detener el proceso, momento en el cual el asunto .999~ = 1 se desmorona. Disparates. ^[47]

Un artículo de Slate informa que el concepto de 0,999... es "muy discutido en sitios web que van desde foros de mensajes de World of Warcraft hasta foros de Ayn Rand ". ^[48] ​​En la misma línea, la pregunta de 0,999... resultó ser un tema tan popular en los primeros siete años de los foros Battle.net de Blizzard Entertainment que la compañía emitió un "comunicado de prensa" el Día de los Inocentes de 2004 que es 1:

Estamos muy emocionados de cerrar el libro sobre este tema de una vez por todas. Hemos sido testigos de la angustia y la preocupación sobre si .999~ es igual o no a 1, y estamos orgullosos de que la siguiente prueba resuelva de manera definitiva y concluyente el problema para nuestros clientes. ^[49]

Luego se ofrecen dos demostraciones, basadas en límites y multiplicación por 10.

0,999... características también en chistes matemáticos , como por ejemplo: ^[50]

P: ¿Cuántos matemáticos se necesitan para enroscar una bombilla ?

R: 0,999999....

En sistemas numéricos alternativos

Aunque los números reales forman un sistema numérico extremadamente útil , la decisión de interpretar la notación "0,999..." como el nombre de un número real es, en última instancia, una convención, y Timothy Gowers sostiene en Matemáticas: una introducción muy breve que la identidad resultante 0,999. .. = 1 también es una convención:

Sin embargo, de ninguna manera es una convención arbitraria, porque no adoptarla obliga a inventar objetos nuevos y extraños o a abandonar algunas de las reglas familiares de la aritmética. ^[51]

Infinitesimales

Algunas pruebas de que 0,999... = 1 se basan en la propiedad de Arquímedes de los números reales: que no hay infinitesimales distintos de cero . Específicamente, la diferencia 1 − 0,999... debe ser menor que cualquier número racional positivo, por lo que debe ser infinitesimal; pero como los reales no contienen infinitesimales distintos de cero, la diferencia es, por tanto, cero y, por tanto, los dos valores son iguales.

Sin embargo, existen estructuras algebraicas ordenadas matemáticamente coherentes , que incluyen varias alternativas a los números reales, que no son de Arquímedes. El análisis no estándar proporciona un sistema numérico con una gama completa de infinitesimales (y sus inversas). ^[52] AH Lightstone desarrolló una expansión decimal para números hiperreales en (0, 1) ^∗ . ^[53] Lightstone muestra cómo asociar a cada número una secuencia de dígitos,

${\displaystyle 0.d_{1}d_{2}d_{3}\dots ;\dots d_{\infty -1}d_{\infty }d_{\infty +1}\dots ,}$

indexado por los números hipernaturales . Si bien no analiza directamente 0,999..., muestra que el número real 1 ⁄ 3 está representado por 0,333...;...333... que es una consecuencia del principio de transferencia . Como consecuencia el número 0,999...;...999... = 1. Con este tipo de representación decimal, no todas las expansiones representan un número. En particular "0.333...;...000..." y "0.999...;...000..." no corresponden a ningún número.

La definición estándar del número 0,999... es el límite de la secuencia 0,9, 0,99, 0,999,... Una definición diferente implica lo que Terry Tao llama ultralímite , es decir, la clase de equivalencia [(0,9, 0,99, 0,999, ...)] de esta secuencia en la construcción de ultrapotencia , que es un número que no llega a 1 por una cantidad infinitesimal. De manera más general, el número hiperreal u _H =0,999...;...999000..., con el último dígito 9 en el rango hipernatural infinito H , satisface una desigualdad estricta u _H < 1. En consecuencia, una interpretación alternativa para "cero seguido por infinitos 9" podría ser

${\displaystyle {\underset {H}{0.\underbrace {999\ldots } }}\;=1\;-\;{\frac {1}{10^{H}}}.}$^[54]

Todas estas interpretaciones de "0,999..." son infinitamente cercanas a 1. Ian Stewart caracteriza esta interpretación como una forma "completamente razonable" de justificar rigurosamente la intuición de que "falta un poquito" de 1 en 0,999... ^{[ 55]} Junto con Katz y Katz, Robert Ely también cuestiona la suposición de que las ideas de los estudiantes sobre 0,999... < 1 sean intuiciones erróneas sobre los números reales, interpretándolas más bien como intuiciones no estándar que podrían ser valiosas en el aprendizaje del cálculo. ^{[56] [57]}

Hackenbush

La teoría de juegos combinatoria también proporciona reales alternativos, con el infinito Azul-Rojo Hackenbush como un ejemplo particularmente relevante. En 1974, Elwyn Berlekamp describió una correspondencia entre cadenas de Hackenbush y expansiones binarias de números reales, motivado por la idea de compresión de datos . Por ejemplo, el valor de la cadena Hackenbush LRRLRLRL... es 0,010101 ₂ ... =  1 ⁄ 3 . Sin embargo, el valor de LRLLL... (correspondiente a 0,111... ₂ ) es infinitamente menor que 1. La diferencia entre los dos es el número surrealista 1 ⁄ ω , donde ω es el primer ordinal infinito ; el juego relevante es LRRRR... o 0.000... ₂ . ^[58]

De hecho, esto es cierto para las expansiones binarias de muchos números racionales, donde los valores de los números son iguales pero las correspondientes rutas del árbol binario son diferentes. Por ejemplo, 0.10111... ₂  = 0.11000... ₂ , ambos son iguales a 3/4, pero la primera representación corresponde a la ruta del árbol binario LRLRLLL... mientras que la segunda corresponde a la ruta diferente LRLLRRR... .

Revisando la resta

Otra manera en la que las pruebas podrían verse socavadas es si 1 − 0,999... simplemente no existe, porque la resta no siempre es posible. Las estructuras matemáticas con una operación de suma pero no de resta incluyen semigrupos conmutativos , monoides conmutativos y semirings . Richman considera dos de estos sistemas, diseñados de modo que 0,999... < 1.

Primero, Richman define un número decimal no negativo como una expansión decimal literal. Define el orden lexicográfico y una operación de suma, señalando que 0,999... < 1 simplemente porque 0 < 1 en el lugar de las unidades, pero para cualquier x no terminante , se tiene 0,999... +  x  = 1 +  x . Entonces, una peculiaridad de los números decimales es que la suma no siempre se puede cancelar; otra es que ningún número decimal corresponde a 1 ⁄ 3 . Después de definir la multiplicación, los números decimales forman un semicírculo conmutativo positivo, totalmente ordenado. ^[59]

En el proceso de definir la multiplicación, Richman también define otro sistema que llama "corte D ", que es el conjunto de cortes de Dedekind de fracciones decimales. Normalmente esta definición conduce a los números reales, pero para una fracción decimal d permite tanto el corte (−∞,  d ) como el "corte principal" (−∞,  d ]. El resultado es que los números reales "viven con inquietud" junto con" las fracciones decimales. De nuevo 0,999... < 1. No hay infinitesimales positivos en el corte D , pero hay "una especie de infinitesimal negativo", 0 ⁻ , que no tiene expansión decimal. Concluye que 0,999.. . = 1 + 0 ⁻ , mientras que la ecuación "0,999... + x = 1" no tiene solución. ^[60]

números p -ádicos

Cuando se les pregunta acerca de 0,999..., los principiantes a menudo creen que debería haber un "9 final", creyendo que 1 − 0,999... es un número positivo que escriben como "0,000...1". Tenga o no sentido, el objetivo intuitivo es claro: agregar un 1 al 9 final en 0,999... convertiría todos los 9 en 0 y dejaría un 1 en el lugar de las unidades. Entre otras razones, esta idea falla porque no hay un "9 final" en 0,999.... ^[61] Sin embargo, hay un sistema que contiene una cadena infinita de 9, incluido un último 9.

Los enteros de 4 ádicos (puntos negros), incluida la secuencia (3, 33, 333, ...) que convergen en −1. El análogo de 10 ádicos es ...999 = −1.

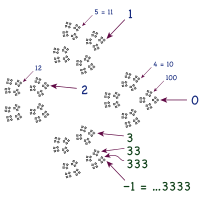
Los números p -ádicos son un sistema numérico alternativo de interés en la teoría de números . Al igual que los números reales, los números p -ádicos se pueden construir a partir de números racionales mediante secuencias de Cauchy ; la construcción utiliza una métrica diferente en la que 0 está más cerca de p y mucho más cerca de p ⁿ que de 1. Los números p -ádicos forman un campo para p primos y un anillo para otros p , incluido 10. Entonces, la aritmética se puede realizar en los p -ádicos y no hay infinitesimales.

En los números de 10 ádicos, los análogos de las expansiones decimales van hacia la izquierda. La expansión de 10 ádicos...999 tiene un último 9, y no tiene un primer 9. Uno puede sumar 1 al lugar de las unidades, y deja solo ceros después de realizarla: 1 +...999 = ...000 = 0, y por lo tanto ...999 = −1. ^[62] Otra derivación utiliza una serie geométrica. La serie infinita implícita en "...999" no converge en los números reales, pero sí en los 10-ádicos, por lo que se puede reutilizar la fórmula familiar:

${\displaystyle \ldots 999=9+9(10)+9(10)^{2}+9(10)^{3}+\cdots ={\frac {9}{1-10}}=-1.}$^[63]

(Compárese con la serie anterior). Una tercera derivación fue inventada por una estudiante de séptimo grado que tenía dudas sobre el argumento limitante de su maestra de que 0,999... = 1, pero se inspiró para tomar la prueba anterior de multiplicar por 10 en la dirección opuesta. : si x  = ...999 entonces 10 x  = ...990, entonces 10 x  =  x  − 9, por lo tanto x  = −1 nuevamente. ^[62]

Como extensión final, dado que 0,999... = 1 (en los reales) y ...999 = −1 (en los 10-ádicos), entonces por "fe ciega y malabarismo descarado de símbolos" ^[64] se puede agregar las dos ecuaciones y llegar a ...999.999... = 0. Esta ecuación no tiene sentido ni como una expansión de 10 ádicos ni como una expansión decimal ordinaria, pero resulta ser significativa y verdadera en la expansión decimal doblemente infinita. del solenoide de 10 ádicos , con extremos izquierdos repetidos para representar los números reales ^[65] y extremos derechos repetidos para representar los números de 10 ádicos.

Preguntas relacionadas

• Las paradojas de Zenón , particularmente la paradoja del corredor, recuerdan la aparente paradoja de que 0,999... y 1 son iguales. La paradoja del corredor se puede modelar matemáticamente y luego, como 0,999..., resolver utilizando una serie geométrica. Sin embargo, no está claro si este tratamiento matemático aborda las cuestiones metafísicas subyacentes que Zenón estaba explorando. ^[66]
• La división por cero ocurre en algunas discusiones populares sobre 0,999.... Casi todos los tratamientos modernos dejan la división por cero sin definir, ya que no se le puede dar ningún significado en los números reales estándar. Sin embargo, la división por cero se define en algunos otros sistemas, como el análisis complejo , donde el plano complejo extendido , es decir, la esfera de Riemann , tiene un " punto en el infinito ". Aquí tiene sentido definir 1 ⁄ 0 como infinito; ^[67] y, de hecho, los resultados son profundos y aplicables a muchos problemas de ingeniería y física. Leonard Euler defendió esa definición mucho antes de que se desarrollara cualquiera de los sistemas numéricos. ^[68]
• El cero negativo es otra característica redundante de muchas formas de escribir números. En sistemas numéricos, como los números reales, donde "0" denota la identidad aditiva y no es ni positivo ni negativo, la interpretación habitual de "-0" es que debería denotar el inverso aditivo de 0, lo que obliga a -0 = 0. ^[69] Sin embargo , algunas aplicaciones científicas utilizan ceros positivos y negativos separados, al igual que algunos sistemas informáticos de números binarios (por ejemplo, números enteros almacenados en formato de signo y magnitud o complemento a uno , o números de punto flotante como lo especifica el estándar IEEE). estándar de puntos ). ^{[70] [71]}

Ver también

• finitismo
• matemáticas informales
• Límite (matemáticas)
• Serie (matemáticas)

Notas

1. Esta definición es equivalente a la definición de números decimales como los límites de sus componentes sumados, que, en el caso de 0,999..., es el límite de la secuencia (0,9, 0,99, 0,999,...). La equivalencia se debe a que las secuencias crecientes acotadas tienen su límite siempre igual a su límite superior mínimo .
2. Stillwell (1994), pág. 42.
3. Peressini y Peressini (2007), pág. 186.
4. Baldwin y Norton 2012; Katz y Katz 2010a.
5. Rudin (1976), pág. 61, Teorema 3.26; Stewart (1999), pág. 706.
6. Euler (1822), pág. 170.
7. Grattan-Guinness (1970), pág. 69; Bonnycastle (1806), pág. 177.
8. Stewart (1999), pág. 706; Rudin (1976), pág. 61; Protter y Morrey (1991), pág. 213; Pugh (2002), pág. 180; Conway (1978), pág. 31.
9. El límite se desprende, por ejemplo, de Rudin (1976), p. 57, Teorema 3.20e. Para un enfoque más directo, véase también Finney, Weir y Giordano (2001), sección 8.1, ejemplo 2(a), ejemplo 6(b).
10. Davies (1846), pág. 175; Smith y Harrington (1895), pág. 115.
11. Beals (2004), pág. 22; Stewart (2009), pág. 34.
12. Bartle y Sherbert (1982), págs. 60–62; Pedrick (1994), pág. 29; Sohrab (2003), pág. 46.
13. Apóstol (1974), págs. 9, 11-12; Beals (2004), pág. 22; Rosenlicht (1985), pág. 27.
14. Apóstol (1974), pág. 12.
15. Griffiths & Hilton (1970), p. xiv y nuevamente por Pugh (2002), p. 10; De hecho, ambos prefieren los cortes de Dedekind a los axiomas. Para el uso de recortes en los libros de texto, ver Pugh (2002), p. 17 o Rudin (1976), pág. 17. Para puntos de vista sobre lógica, ver Pugh (2002), p. 10, Rudin (1976), p.ix, o Munkres (2000), p. 30.
16. Enderton (1977), pág. 113 matiza esta descripción: "La idea detrás de los cortes de Dedekind es que un número real x puede nombrarse dando un conjunto infinito de racionales, es decir, todos los racionales menores que x . De hecho, definiremos x como el conjunto de racionales menores que x". x . Para evitar la circularidad en la definición, debemos poder caracterizar los conjuntos de racionales obtenibles de esta manera..."
17. Rudin (1976), págs. 17-20, Richman (1999), pág. 399, o Enderton (1977), pág. 119. Para ser precisos, Rudin, Richman y Enderton llaman a este corte 1*, 1 ⁻ y 1 _R , respectivamente; los tres lo identifican con el número real tradicional 1. Tenga en cuenta que lo que Rudin y Enderton llaman un corte de Dedekind, Richman lo llama un "corte de Dedekind no principal".
18. Hombre rico (1999), pág. 399.
19. O'Connor y Robertson (2005).
20. Hombre rico (1999).
21. Hombre rico (1999), pág. 398–399.
22. Griffiths y Hilton (1970), pág. 386, §24.2 "Secuencias".
23. Griffiths y Hilton (1970), págs.388, 393.
24. Griffiths y Hilton (1970), pág. 395.
25. Griffiths y Hilton (1970), págs. viii, 395.
26. Li (2011).
27. Artigue (2002), pág. 212.
28. Petkovšek (1990), pág. 408.
29. Protter y Morrey (1991), pág. 503; Bartle y Sherbert (1982), pág. 61.
30. Komornik y Loreti (1998), pág. 636.
31. Kempner (1936), pág. 611; Petkovšek (1990), pág. 409.
32. Petkovšek (1990), págs. 410–411.
33. Leavitt (1984), pág. 301.
34. Lewittes (2006), págs. 1-3; Leavitt (1967), págs. 669, 673; Shrader-Fréchette (1978), págs. 96–98.
35. Pugh (2002), pág. 97; Alligood, Sauer y Yorke (1996), págs. 150-152; Protter y Morrey (1991), pág. 507; Pedrick (1994), pág. 29.
36. Maor (1987), pág. 60 y Mankiewicz (2000), pág. 151 revisan el método anterior; Mankiewicz se lo atribuye a Cantor, pero la fuente principal no está clara. Munkres (2000), pág. 50 menciona este último método.
37. Rudin (1976), pág. 50; Pugh (2002), pág. 98.
38. Manojo (1982), pág. 119; Alto y Schwarzenberger (1978), pág. 6. La última sugerencia se debe a Burrell (1998), p. 28: "Quizás el más tranquilizador de todos los números es el 1... Por eso es especialmente inquietante cuando alguien intenta hacer pasar 0,9~ por 1".
39. Alto y Schwarzenberger (1978), págs. 6–7; Alto (2000), pág. 221.
40. Alto y Schwarzenberger (1978), pág. 6; Alto (2000), pág. 221.
41. Alto (2000), pág. 221.
42. Alto (1976), págs. 10-14.
43. Pinto y alto (2001), pág. 5; Edwards y Ward (2004), págs. 416–417.
44. Mazur (2005), págs. 137-141.
45. Dubinsky y col. (2005), págs. 261–262.
46. Como lo observó Richman (p. 396). de Vreught, Hans (1994). "Preguntas frecuentes sobre sci.math: ¿Por qué 0,9999... = 1?". Archivado desde el original el 29 de septiembre de 2007 . Consultado el 29 de junio de 2006 .
47. Adams, Cecil (11 de julio de 2003). "Una pregunta infinita: ¿Por qué .999~ = 1?". La droga heterosexual . Lector de Chicago . Archivado desde el original el 15 de agosto de 2006 . Consultado el 6 de septiembre de 2006 .
48. Ellenberg, Jordania (6 de junio de 2014). "¿0,999... = 1? ¿Y las series divergentes son una invención del diablo?". Pizarra .
49. "Blizzard Entertainment anuncia .999 ~ (repetido) = 1" (Presione soltar). Blizzard Entertainment. 1 de abril de 2004. Archivado desde el original el 4 de noviembre de 2009 . Consultado el 16 de noviembre de 2009 .
50. Renteln y Dundes, pag. 27
51. Gowers pag. 60
52. Para obtener un tratamiento completo de los números no estándar, consulte, por ejemplo, el Análisis no estándar de Robinson .
53. Piedra de luz págs. 245-247
54. Katz y Katz 2010
55. Stewart 2009, pag. 175; la discusión completa de 0,999... se extiende a lo largo de las páginas 172-175.
56. Katz y Katz (2010b)
57. R. Ely (2010)
58. Berlekamp, ​​Conway y Guy (págs. 79–80, 307–311) analizan 1 y 1 ⁄ 3 y tocan 1 ⁄ ω . El juego de 0,111... ₂ se deriva directamente de la regla de Berlekamp.
59. Hombre rico págs. 397–399
60. Hombre rico págs. 398–400. Rudin (p. 23) asigna esta construcción alternativa (pero sobre las racionales) como el último ejercicio del Capítulo 1.
61. Gardiner pág. 98; Gowers pág. 60
62. Fjelstad pág. 11
63. Fjelstad págs. 14-15
64. DeSua pag. 901
65. DeSua págs. 902–903
66. Wallace pág. 51, maorí pág. 17
67. Véase, por ejemplo, el tratamiento que hace JB Conway de las transformaciones de Möbius, págs. 47-57.
68. Maor pág. 54
69. Munkres pag. 34, Ejercicio 1(c)
70. Kroemer, Herbert; Kittel, Charles (1980). Física térmica (2e ed.). WH Freeman. pag. 462.ISBN _ 978-0-7167-1088-2.
71. "Tipos de coma flotante". Especificación del lenguaje MSDN C# . Archivado desde el original el 24 de agosto de 2006 . Consultado el 29 de agosto de 2006 .

Referencias

• Alligood, KT; Sauer, TD; Yorke, JA (1996). "4.1 Conjuntos de Cantor". Caos: una introducción a los sistemas dinámicos . Saltador. ISBN 978-0-387-94677-1.

  Este libro de texto introductorio sobre sistemas dinámicos está dirigido a estudiantes universitarios y principiantes de posgrado. (pág. ix)

• Apóstol, Tom M. (1974). Análisis matemático (2e ed.). Addison-Wesley. ISBN 978-0-201-00288-1.

  Una transición del cálculo al análisis avanzado, el análisis matemático pretende ser "honesto, riguroso, actualizado y, al mismo tiempo, no demasiado pedante". (pref.) El desarrollo de Apostol de los números reales utiliza el axioma del límite superior mínimo e introduce decimales infinitos dos páginas después. (págs. 9 a 11)

• Artigue, Michèle (2002). Holton, Derek; Artigue, Michèle; Kirchgräber, Urs; Hilel, Joel; Niss, Mogens; Schoenfeld, Alan (eds.). La Enseñanza y el Aprendizaje de las Matemáticas en el Nivel Universitario . Nueva serie de estudios ICMI. vol. 7. Springer, Dordrecht. doi :10.1007/0-306-47231-7. ISBN 978-0-306-47231-2.
• Baldwin, Michael; Norton, Anderson (2012). "¿0,999... realmente es igual a 1?". El Educador Matemático . 21 (2): 58–67.
• Bartle, RG ; Sherbert, DR (1982). Introducción al Análisis Real. Wiley. ISBN 978-0-471-05944-8.

  Este texto pretende ser "un libro de texto accesible y de ritmo razonable que trate los conceptos y técnicas fundamentales del análisis real". Su desarrollo de los números reales se basa en el axioma supremo. (págs. vii-viii)

• Beals, Richard (2004). Análisis: una introducción. Cambridge UP. ISBN 978-0-521-60047-7.
• Berlekamp, ​​ER ; Conway, JH ; Chico, RK (1982). Maneras de Ganar para tus Jugadas Matemáticas . Prensa académica. ISBN 978-0-12-091101-1.
• Berz, Martín (1992). Diferenciación automática como análisis no arquimediano . Métodos de envolvente y aritmética informática. Elsevier. págs. 439–450. CiteSeerX  10.1.1.31.3019 .
• Bonnycastle, Juan (1806). Una introducción al álgebra; con notas y observaciones: diseñado para el uso de escuelas y lugares de educación pública (Primera edición estadounidense). Filadelfia.
• Manojo, Bryan H. (1982). Falacias y paradojas matemáticas. Van Nostrand Reinhold. ISBN 978-0-442-24905-2.

  Este libro presenta un análisis de paradojas y falacias como herramienta para explorar su tema central, "la relación bastante tenue entre la realidad matemática y la realidad física". Se supone álgebra del primer año de secundaria; En el libro se desarrollan más matemáticas, incluidas las series geométricas en el Capítulo 2. Aunque 0,999... no es una de las paradojas que deben tratarse en su totalidad, se menciona brevemente durante el desarrollo del método diagonal de Cantor. (págs. ix-xi, 119)

• Burrell, Brian (1998). Guía de Merriam-Webster para las matemáticas cotidianas: una referencia para el hogar y los negocios. Merriam Webster. ISBN 978-0-87779-621-3.
• Byers, William (2007). Cómo piensan los matemáticos: utilizar la ambigüedad, la contradicción y la paradoja para crear matemáticas. Princeton ARRIBA. ISBN 978-0-691-12738-5.
• Conway, John B. (1978) [1973]. Funciones de una variable compleja I (2e ed.). Springer-Verlag. ISBN 978-0-387-90328-6.

  Este texto asume como requisito previo "un curso estricto de cálculo básico"; sus principios declarados son presentar análisis complejos como "Una introducción a las matemáticas" y exponer el material de forma clara y precisa. (pág. vii)

• Davies, Charles (1846). La aritmética universitaria: abrazando la ciencia de los números y sus numerosas aplicaciones. AS Barnes. pag. 175 . Consultado el 4 de julio de 2011 .
• DeSua, Frank C. (noviembre de 1960). "Un sistema isomorfo a los reales". El Mensual Matemático Estadounidense . 67 (9): 900–903. doi :10.2307/2309468. JSTOR  2309468.
• Dubinsky, Ed; Bueno, Kirk; McDonald, Michael; Marrón, Ana (2005). "Algunas cuestiones históricas y paradojas sobre el concepto de infinito: un análisis APOS: parte 2". Estudios Educativos en Matemáticas . 60 (2): 253–266. doi :10.1007/s10649-005-0473-0. S2CID  45937062.
• Edwards, Bárbara; Ward, Michael (mayo de 2004). "Sorpresas de la investigación en educación matemática: (mal) uso de las definiciones matemáticas por parte de los estudiantes" (PDF) . El Mensual Matemático Estadounidense . 111 (5): 411–425. CiteSeerX  10.1.1.453.7466 . doi :10.2307/4145268. JSTOR  4145268. Archivado desde el original (PDF) el 22 de julio de 2011 . Consultado el 4 de julio de 2011 .
• Enderton, Herbert B. (1977). Elementos de la teoría de conjuntos. Elsevier. ISBN 978-0-12-238440-0.

  Un libro de texto de introducción a la teoría de conjuntos que "no presupone antecedentes específicos". Está escrito para dar cabida a un curso centrado en la teoría de conjuntos axiomáticos o en la construcción de sistemas numéricos; el material axiomático está marcado de manera que se le pueda restar importancia. (págs. xi-xii)

• Euler, Leonhard (1822) [1770]. Elementos de álgebra. John Hewlett y Francis Horner, traductores de inglés (3.ª ed. en inglés). Orme Longman. pag. 170.ISBN _ 978-0-387-96014-2. Consultado el 4 de julio de 2011 .
• Finney, Ross L.; Weir, Muarice D.; Giordano, Frank tR. (2001). Cálculo de Thomas: primeros trascendentales (10ª ed.). Nueva York: Addison-Wesley.
• Fjelstad, Paul (enero de 1995). "La paradoja del entero repetido". La revista universitaria de matemáticas . 26 (1): 11-15. doi :10.2307/2687285. JSTOR  2687285.
• Gardiner, Anthony (2003) [1982]. Comprensión del infinito: las matemáticas de los procesos infinitos. Dover. ISBN 978-0-486-42538-2.
• Gowers, Timoteo (2002). Matemáticas: una introducción muy breve. Oxford ARRIBA. ISBN 978-0-19-285361-5.
• Grattan-Guinness, Ivor (1970). El desarrollo de los fundamentos del análisis matemático de Euler a Riemann. Prensa del MIT. ISBN 978-0-262-07034-8.
• Griffiths, HB; Hilton, PJ (1970). Un libro de texto completo de matemáticas clásicas: una interpretación contemporánea . Londres: Van Nostrand Reinhold. ISBN 978-0-442-02863-3. LCC  QA37.2 G75.

  Este libro surgió de un curso para profesores de matemáticas de escuelas primarias del área de Birmingham . El curso pretendía transmitir una perspectiva a nivel universitario sobre las matemáticas escolares , y el libro está dirigido a estudiantes "que han alcanzado aproximadamente el nivel de completar un año de estudios matemáticos especializados en una universidad". Los números reales se construyen en el Capítulo 24, "quizás el capítulo más difícil de todo el libro", aunque los autores atribuyen gran parte de la dificultad al uso de la teoría ideal , que no se reproduce aquí. (págs. vii, xiv)

• Katz, K.; Katz, M. (2010a). "¿Cuándo es .999... menos que 1?". "El entusiasta de las matemáticas de Montana ". 7 (1): 3–30. arXiv : 1007.3018 . Código Bib : 2010arXiv1007.3018U. doi : 10.54870/1551-3440.1381. S2CID  11544878. Archivado desde el original el 20 de julio de 2011 . Consultado el 4 de julio de 2011 .
• Katz, Karin Usadi; Katz, Mikhail G. (2010b). "Acercándonos al infinitesimal 1 - .9 ... en una era post-triunvirato". Estudios Educativos en Matemáticas . 74 (3): 259. arXiv : 1003.1501 . Código Bib : 2010arXiv1003.1501K. doi :10.1007/s10649-010-9239-4. S2CID  115168622.
• Kempner, AJ (diciembre de 1936). "Sistemas anormales de numeración". El Mensual Matemático Estadounidense . 43 (10): 610–617. doi :10.2307/2300532. JSTOR  2300532.
• Komornik, Vilmos; Loreti, Paola (1998). "Desarrollos únicos en bases no enteras". El Mensual Matemático Estadounidense . 105 (7): 636–639. doi :10.2307/2589246. JSTOR  2589246.
• Li, Liangpan (marzo de 2011). "Un nuevo enfoque de los números reales". arXiv : 1101.1800 [matemáticas.CA].
• Leavitt, WG (1967). "Un teorema sobre decimales repetidos". El Mensual Matemático Estadounidense . 74 (6): 669–673. doi :10.2307/2314251. JSTOR  2314251.
• Leavitt, WG (septiembre de 1984). "Decimales repetidos". La revista universitaria de matemáticas . 15 (4): 299–308. doi :10.2307/2686394. JSTOR  2686394.
• Lewittes, José (2006). "Teorema de Midy para decimales periódicos". arXiv : math.NT/0605182 .
• Lightstone, AH (marzo de 1972). "Infinitesimales". El Mensual Matemático Estadounidense . 79 (3): 242–251. doi :10.2307/2316619. JSTOR  2316619.
• Mankiewicz, Richard (2000). La historia de las matemáticas. Cassell. ISBN 978-0-304-35473-3.

  Mankiewicz busca representar "la historia de las matemáticas en un estilo accesible" combinando aspectos visuales y cualitativos de las matemáticas, escritos de matemáticos y bocetos históricos. (pág. 8)

• Maor, Eli (1987). Hasta el infinito y más allá: una historia cultural del infinito . Birkhäuser. ISBN 978-3-7643-3325-6.

  Este libro, una revisión temática más que cronológica del infinito, está "destinado al lector en general" pero "contado desde el punto de vista de un matemático". Sobre el dilema entre rigor versus lenguaje legible, Maor comenta: "Espero haber logrado abordar adecuadamente este problema". (págs. x-xiii)

• Mazur, José (2005). Euclides en la selva tropical: descubriendo verdades universales en lógica y matemáticas. Pearson: Prensa Pi. ISBN 978-0-13-147994-4.
• Munkres, James R. (2000) [1975]. Topología (2e ed.). Prentice Hall. ISBN 978-0-13-181629-9.

  Pensado como una introducción "a nivel de posgrado de primer año o de último año" sin requisitos previos formales: "Ni siquiera asumo que el lector sepa mucho de la teoría de conjuntos". (p. xi) El tratamiento que hace Munkres de los reales es axiomático; Afirma sobre las construcciones hechas con las manos desnudas: "Esta forma de abordar el tema requiere mucho tiempo y esfuerzo y tiene más interés lógico que matemático". (pág. 30)

• Navarro, María Ángeles; Carreras, Pedro Pérez (2010). «Una propuesta metodológica socrática para el estudio de la igualdad 0,999...=1» (PDF) . La Enseñanza de las Matemáticas . 13 (1): 17–34 . Consultado el 4 de julio de 2011 .
• Núñez, Rafael (2006). "¿Se mueven realmente los números reales? Lenguaje, pensamiento y gestos: los fundamentos cognitivos incorporados de las matemáticas". "18 ensayos no convencionales sobre la naturaleza de las matemáticas ". Saltador. págs. 160-181. ISBN 978-0-387-25717-4. Archivado desde el original el 18 de julio de 2011 . Consultado el 4 de julio de 2011 .
• O'Connor, JJ; Robertson, EF (octubre de 2005). "Tema de historia: los números reales: Stevin a Hilbert". MacTutor Historia de las Matemáticas . Archivado desde el original el 29 de septiembre de 2007 . Consultado el 30 de agosto de 2006 .
• Pedrick, George (1994). Un primer curso de análisis . Saltador. ISBN 978-0-387-94108-0.
• Peressini, Antonio; Peressini, Domingo (2007). "Filosofía de la Matemática y Educación Matemática". En van Kerkhove, Bart; van Bendegem, Jean Paul (eds.). Perspectivas sobre las prácticas matemáticas. Lógica, epistemología y unidad de la ciencia. vol. 5. Saltador. ISBN 978-1-4020-5033-6.
• Petkovšek, Marko (mayo de 1990). "Los números ambiguos son densos". Mensual Matemático Estadounidense . 97 (5): 408–411. doi :10.2307/2324393. JSTOR  2324393.
• Pinto, Márcia; Alto, David (2001). PME25: Seguimiento del desarrollo de los estudiantes en un curso de análisis universitario tradicional (PDF) . págs. v4: 57–64. Archivado desde el original (PDF) el 30 de mayo de 2009 . Consultado el 3 de mayo de 2009 .
• Protter, MH ; Morrey, Charles B. Jr. (1991). Un primer curso de análisis real (2e ed.). Saltador. ISBN 978-0-387-97437-8.

  Este libro tiene como objetivo "presentar una base teórica de análisis que sea adecuada para estudiantes que hayan completado un curso estándar de cálculo". (p. vii) Al final del Capítulo 2, los autores asumen como axioma para los números reales que las secuencias acotadas y no decrecientes convergen, demostrando luego el teorema de los intervalos anidados y la propiedad del límite superior mínimo. (págs. 56–64) Las expansiones decimales aparecen en el Apéndice 3, "Expansiones de números reales en cualquier base". (págs. 503–507)

• Pugh, Charles Chapman (2002). Análisis matemático real. Springer-Verlag. ISBN 978-0-387-95297-0.

  Si bien asume estar familiarizado con los números racionales, Pugh introduce los cortes de Dedekind lo antes posible y dice sobre el tratamiento axiomático: "Esto es una especie de fraude, considerando que toda la estructura de análisis se basa en el sistema de números reales". (p. 10) Después de demostrar la propiedad del límite superior mínimo y algunos hechos relacionados, los cortes no se utilizan en el resto del libro.

• Renteln, Paul; Dundes, Alan (enero de 2005). "Infalible: una muestra de humor popular matemático" (PDF) . Avisos de la AMS . 52 (1): 24–34. Archivado desde el original (PDF) el 25 de febrero de 2009 . Consultado el 3 de mayo de 2009 .
• Richman, Fred (diciembre de 1999). "¿Es 0,999... = 1?". Revista Matemáticas . 72 (5): 396–400. doi :10.2307/2690798. JSTOR  2690798.Preimpresión HTML gratuita: Richman, Fred (junio de 1999). "¿Es 0,999... = 1?". Archivado desde el original el 2 de septiembre de 2006 . Consultado el 23 de agosto de 2006 .Nota: el artículo de la revista contiene material y redacción que no se encuentran en la preimpresión.
• Robinson, Abraham (1996). Análisis no estándar (edición revisada). Prensa de la Universidad de Princeton. ISBN 978-0-691-04490-3. JSTOR  j.ctt1cx3vb6.
• Rosenlicht, Maxwell (1985). Introducción al análisis. Dover. ISBN 978-0-486-65038-8.Este libro ofrece una introducción "cuidadosa y rigurosa" al análisis real. Da los axiomas de los números reales y luego los construye (págs. 27-31) como decimales infinitos con 0,999... = 1 como parte de la definición.
• Rudin, Walter (1976) [1953]. Principios del análisis matemático (3e ed.). McGraw-Hill. ISBN 978-0-07-054235-8.

  Un libro de texto para un curso universitario avanzado. "La experiencia me ha convencido de que es pedagógicamente incorrecto (aunque lógicamente correcto) comenzar con la construcción de los números reales a partir de los racionales. Al principio, la mayoría de los estudiantes simplemente no aprecian la necesidad de hacerlo. En consecuencia, los números reales El sistema numérico se introduce como un campo ordenado con la propiedad de límite superior mínimo y rápidamente se hacen algunas aplicaciones interesantes de esta propiedad. Sin embargo, no se omite la construcción de Dedekind. Ahora se encuentra en un Apéndice del Capítulo 1, donde puede ser estudiado y disfrutado cuando llegue el momento." (pág. ix)

• Shrader-Frechette, Maurice (marzo de 1978). "Números racionales complementarios". Revista Matemáticas . 51 (2): 90–98. doi :10.2307/2690144. JSTOR  2690144.
• Smith, Carlos; Harrington, Charles (1895). Aritmética para las escuelas. Macmillan. pag. 115.ISBN _ 978-0-665-54808-6. Consultado el 4 de julio de 2011 .
• Sohrab, Houshang (2003). Análisis Real Básico. Birkhäuser. ISBN 978-0-8176-4211-2.
• Starbird, M .; Starbird, T. (marzo de 1992). "Redundancia requerida en la representación de reales". Actas de la Sociedad Matemática Estadounidense . 114 (3): 769–774. doi : 10.1090/S0002-9939-1992-1086343-5 . JSTOR  2159403.
• Stewart, Ian (1977). Los fundamentos de las matemáticas. Oxford ARRIBA. ISBN 978-0-19-853165-4.
• Stewart, Ian (2009). El tesoro de tesoros matemáticos del profesor Stewart. Libros de perfil. ISBN 978-1-84668-292-6.
• Stewart, James (1999). Cálculo: primeros trascendentales (4e ed.). Brooks/Cole. ISBN 978-0-534-36298-0.

  Este libro tiene como objetivo "ayudar a los estudiantes a descubrir el cálculo" y "fomentar la comprensión conceptual". (p. v) Omite pruebas de los fundamentos del cálculo.

• Stillwell, John (1994), Elementos de álgebra: geometría, números, ecuaciones, Springer, ISBN 9783540942900
• Alto, David ; Schwarzenberger, RLE (1978). "Conflictos en el aprendizaje de los números reales y los límites" (PDF) . Enseñanza de las Matemáticas . 82 : 44–49. Archivado desde el original (PDF) el 30 de mayo de 2009 . Consultado el 3 de mayo de 2009 .
• Alto, David (1976). «Conflictos y Catástrofes en el Aprendizaje de las Matemáticas» (PDF) . Educación Matemática para la Enseñanza . 2 (4): 2–18. Archivado desde el original (PDF) el 26 de marzo de 2009 . Consultado el 3 de mayo de 2009 .
• Alto, David (2000). "Desarrollo cognitivo en matemáticas avanzadas utilizando tecnología" (PDF) . Revista de investigación en educación matemática . 12 (3): 210–230. Código Bib : 2000MEdRJ..12..196T. doi :10.1007/BF03217085. S2CID  143438975. Archivado desde el original (PDF) el 30 de mayo de 2009 . Consultado el 3 de mayo de 2009 .
• von Mangoldt, Hans (1911). "Reihenzahlen". Einführung in die höhere Mathematik (en alemán) (1ª ed.). Leipzig: Verlag von S. Hirzel.
• Wallace, David Foster (2003). Todo y más: una historia compacta del infinito. Norton. ISBN 978-0-393-00338-3.

Otras lecturas

• Beswick, Kim (2004). "¿Por qué 0,999... = 1?: Una pregunta perenne y sentido numérico". Profesor de Matemáticas de Australia . 60 (4): 7–9.
• Burkov, SE (1987). "Modelo unidimensional de la aleación cuasicristalina". Revista de Física Estadística . 47 (3/4): 409–438. Código Bib : 1987JSP....47..409B. doi :10.1007/BF01007518. S2CID  120281766.
• Burn, Bob (marzo de 1997). "81.15 Un caso de conflicto". La Gaceta Matemática . 81 (490): 109-112. doi :10.2307/3618786. JSTOR  3618786. S2CID  187823601.
• Calvert, JB; Tuttle, ER; Martín, Michael S.; Warren, Peter (febrero de 1981). "La era de Newton: un curso intensivo interdisciplinario". El Profesor de Historia . 14 (2): 167–190. doi :10.2307/493261. JSTOR  493261.
• Choi, Younggi; Hacer, Jonghoon (noviembre de 2005). "Igualdad involucrada en 0,999... y (-8)1/3". Para el Aprendizaje de las Matemáticas . 25 (3): 13–15, 36. JSTOR  40248503.
• Choong, KY; Daykin, DE; Rathbone, CR (abril de 1971). "Aproximaciones racionales a π". Matemáticas de la Computación . 25 (114): 387–392. doi :10.2307/2004936. JSTOR  2004936.
• Edwards, B. (1997). "La comprensión y el uso de definiciones matemáticas por parte de un estudiante universitario en análisis reales". En Dossey, J.; Swafford, JO; Parmentier, M.; Dossey, AE (eds.). Actas de la 19ª Reunión Anual del Capítulo Norteamericano del Grupo Internacional para la Psicología de la Educación Matemática . vol. 1. Columbus, OH: Centro de intercambio de información ERIC para ciencias, matemáticas y educación ambiental. págs. 17-22.
• Eisenmann, Petr (2008). "¿Por qué no es cierto que 0,999... < 1?" (PDF) . La Enseñanza de las Matemáticas . 11 (1): 35–40 . Consultado el 4 de julio de 2011 .
• Ely, Robert (2010). "Concepciones estudiantiles atípicas sobre los infinitesimales". Revista de Investigación en Educación Matemática . 41 (2): 117-146. doi :10.5951/jresematheduc.41.2.0117.

  Este artículo es un estudio de campo que involucra a una estudiante que desarrolló una teoría de los infinitesimales al estilo Leibniziano para ayudarla a comprender el cálculo y, en particular, a explicar 0,999... que está por debajo de 1 por un infinitesimal 0,000...1.

• Ferrini-Mundy, J.; Graham, K. (1994). Kaput, J.; Dubinsky, E. (eds.). "Investigación en el aprendizaje del cálculo: Comprensión de límites, derivadas e integrales". Notas de la MAA: cuestiones de investigación en el aprendizaje de matemáticas de pregrado . 33 : 31–45.
• Gardiner, Tony (junio de 1985). "Procesos infinitos en matemáticas elementales: ¿Cuánto debemos decirles a los niños?". La Gaceta Matemática . 69 (448): 77–87. doi :10.2307/3616921. JSTOR  3616921. S2CID  125222118.\
• Monaghan, John (diciembre de 1988). "Matemáticas reales: un aspecto del futuro del A-Level". La Gaceta Matemática . 72 (462): 276–281. doi :10.2307/3619940. JSTOR  3619940. S2CID  125825964.
• Przenioslo, Malgorzata (marzo de 2004). "Imágenes del límite de función formadas en el curso de estudios matemáticos en la universidad". Estudios Educativos en Matemáticas . 55 (1–3): 103–132. doi :10.1023/B:EDUC.0000017667.70982.05. S2CID  120453706.
• Sandefur, James T. (febrero de 1996). "Uso de la autosemejanza para encontrar longitud, área y dimensión". El Mensual Matemático Estadounidense . 103 (2): 107–120. doi :10.2307/2975103. JSTOR  2975103.
• Sierpińska, Anna (noviembre de 1987). "Los estudiantes de humanidades y los obstáculos epistemológicos relacionados con los límites". Estudios Educativos en Matemáticas . 18 (4): 371–396. doi :10.1007/BF00240986. JSTOR  3482354. S2CID  144880659.
• Szydlik, Jennifer Earles (mayo de 2000). "Creencias matemáticas y comprensión conceptual del límite de una función". Revista de Investigación en Educación Matemática . 31 (3): 258–276. doi :10.2307/749807. JSTOR  749807.
• Alto, David O. (2009). "Matemáticas dinámicas y combinación de estructuras de conocimiento en el cálculo". Educación Matemática ZDM . 41 (4): 481–492. doi :10.1007/s11858-009-0192-6. S2CID  14289039.
• Alto, David O. (mayo de 1981). "Intuiciones del infinito". Matemáticas en la escuela . 10 (3): 30–33. JSTOR  30214290.

enlaces externos

Escuche este artículo ( 50 minutos )

Este archivo de audio se creó a partir de una revisión de este artículo con fecha del 19 de octubre de 2006 y no refleja ediciones posteriores. (2006-10-19)

( Ayuda de audio  · Más artículos hablados )

• .999999... = 1? de Cortar el nudo
• ¿Por qué 0,9999... = 1?
• Prueba de la igualdad basada en aritmética.
• La investigación de David Tall sobre la cognición matemática.
• ¿Qué tiene de malo pensar en los números reales como decimales infinitos?
• Teorema 0.999... sobre Metamath