Leyes de la forma

1969 non-fiction book by G. Spencer-Brown

Leyes de la forma (en adelante, Leyes de la forma ) es un libro de G. Spencer-Brown , publicado en 1969, que se sitúa en la frontera entre las matemáticas y la filosofía . Leyes de la forma describe tres sistemas lógicos distintos :

• La "aritmética primaria" (descrita en el Capítulo 4 de LoF ), cuyos modelos incluyen la aritmética booleana ;
• El " álgebra primaria " (Capítulo 6 de LoF ), cuyos modelos incluyen el álgebra de Boole de dos elementos (en adelante abreviada 2 ), la lógica de Boole y el cálculo proposicional clásico ;
• "Ecuaciones de segundo grado" (Capítulo 11), cuyas interpretaciones incluyen autómatas finitos y la Aritmética Recursiva Restringida (RRA) de Alonzo Church .

"Álgebra de límites" es el término de Meguire (2011) ^[1] para la unión del álgebra primaria y la aritmética primaria. Laws of Form a veces se refiere vagamente al "álgebra primaria" así como a LoF .

Biblia

El prefacio afirma que el trabajo se exploró por primera vez en 1959, y Spencer Brown cita a Bertrand Russell como partidario de su esfuerzo. También agradece a JCP Miller, del University College de Londres, por ayudar con la corrección de pruebas y ofrecer otras orientaciones. En 1963, Harry Frost, profesor titular de ciencias físicas en el departamento de Estudios Extramuros de la Universidad de Londres , invitó a Spencer Brown a impartir un curso sobre las matemáticas de la lógica.

LoF surgió del trabajo en ingeniería electrónica que su autor realizó alrededor de 1960, y de las conferencias posteriores sobre lógica matemática que dio bajo los auspicios del programa de extensión de la Universidad de Londres . LoF ha aparecido en varias ediciones. La segunda serie de ediciones apareció en 1972 con el "Prefacio a la primera edición estadounidense", que enfatizaba el uso de paradojas autorreferenciales, ^[2] y la más reciente es una traducción alemana de 1997. LoF nunca ha dejado de imprimirse.

La prosa mística y declamatoria de LoF y su amor por la paradoja hacen que sea una lectura desafiante para todos. Spencer-Brown fue influenciado por Wittgenstein y RD Laing . LoF también se hace eco de una serie de temas de los escritos de Charles Sanders Peirce , Bertrand Russell y Alfred North Whitehead .

La obra ha tenido efectos curiosos en algunas clases de lectores; por ejemplo, sobre bases oscuras, se ha afirmado que todo el libro está escrito de manera operativa, dando instrucciones al lector en lugar de decirle qué "es", y que de acuerdo con el interés de G. Spencer-Brown en las paradojas, la única oración que hace una declaración de que algo es , es la declaración que dice que no se usan tales declaraciones en este libro. ^[3] Además, la afirmación afirma que, a excepción de esta oración, el libro puede verse como un ejemplo de E-Prime . Lo que motivó tal afirmación es oscuro, ya sea en términos de incentivo, mérito lógico o de hecho, porque el libro usa rutinaria y naturalmente el verbo to be en todo momento y en todas sus formas gramaticales, como se puede ver tanto en el original como en las citas que se muestran a continuación. ^[4]

Recepción

En apariencia, una obra de filosofía y matemática formal, LoF se convirtió en una especie de clásico de culto : fue elogiado por Heinz von Foerster cuando lo revisó para el Whole Earth Catalog . ^[5] Aquellos que están de acuerdo señalan a LoF como la encarnación de una enigmática "matemática de la conciencia ", cuyo simbolismo algebraico captura una (quizás incluso "la") raíz implícita de la cognición : la capacidad de "distinguir". LoF sostiene que el álgebra primaria revela sorprendentes conexiones entre la lógica , el álgebra de Boole y la aritmética, y la filosofía del lenguaje y la mente .

Stafford Beer escribió en una reseña para Nature : "Cuando uno piensa en todo lo que Russell atravesó hace sesenta años para escribir los Principia , y todo lo que nosotros, sus lectores, pasamos al luchar con esos tres vastos volúmenes, es casi triste". ^[6]

Banaschewski (1977) ^[7] sostiene que el álgebra primaria no es más que una nueva notación para el álgebra de Boole. De hecho, el álgebra de Boole de dos elementos 2 puede considerarse como la interpretación prevista del álgebra primaria. Sin embargo, la notación del álgebra primaria:

• Explota al máximo la dualidad que caracteriza no sólo a las álgebras de Boole sino a todas las redes ;
• Destaca cómo afirmaciones sintácticamente distintas en lógica y 2 pueden tener una semántica idéntica ;
• Simplifica drásticamente los cálculos del álgebra de Boole y las pruebas en lógica sentencial y silogística .

Además, la sintaxis del álgebra primaria puede extenderse a sistemas formales distintos del 2 y de la lógica oracional, lo que da como resultado matemáticas de límites (véase § Trabajo relacionado más abajo).

LoF ha influido, entre otros, en Heinz von Foerster , Louis Kauffman , Niklas Luhmann , Humberto Maturana , Francisco Varela y William Bricken. Algunos de estos autores han modificado el álgebra primaria de maneras muy interesantes.

LoF afirmó que ciertas conjeturas matemáticas bien conocidas y de larga data, como el teorema de los cuatro colores , el último teorema de Fermat y la conjetura de Goldbach , se pueden demostrar utilizando extensiones del álgebra primaria. Spencer-Brown finalmente hizo circular una supuesta prueba del teorema de los cuatro colores, pero se encontró con escepticismo. ^[8]

La forma (Capítulo 1)

El símbolo:

También llamada la "marca" o "cruz", es la característica esencial de las Leyes de la Forma. En el estilo inimitable y enigmático de Spencer-Brown, la Marca simboliza la raíz de la cognición , es decir, la Marca dualista indica la capacidad de diferenciar un "esto" de "todo lo demás excepto esto".

En LoF , una cruz denota el trazado de una "distinción", y puede considerarse como si significara lo siguiente, todo a la vez:

• El acto de trazar un límite alrededor de algo, separándolo así de todo lo demás;
• Aquello que se distingue de todo al trazar el límite;
• Cruzar de un lado al otro del límite.

Las tres formas implican una acción por parte de la entidad cognitiva (por ejemplo, la persona) que hace la distinción. Como dice LoF :

"El primer comando:

• Establezca una distinción

Bien puede expresarse de maneras como:

• Que haya una distinción,
• Encuentra una distinción,
• Ver una distinción,
• Describe una distinción,
• Definir una distinción,

O:

• "Hagamos una distinción". ( LoF , Notas al capítulo 2)

El contrapunto del estado Marcado es el estado No Marcado, que es simplemente nada, el vacío, o el infinito inexpresable representado por un espacio en blanco. Es simplemente la ausencia de una Cruz. No se ha hecho ninguna distinción y no se ha cruzado nada. El estado Marcado y el vacío son los dos valores primitivos de las Leyes de la Forma.

La Cruz puede ser vista como denotando la distinción entre dos estados, uno "considerado como un símbolo" y otro no considerado como tal. De este hecho surge una curiosa resonancia con algunas teorías de la conciencia y el lenguaje . Paradójicamente, la Forma es a la vez Observador y Observado, y es también el acto creativo de hacer una observación. LoF (excluyendo el material posterior) cierra con las palabras:

...la primera distinción, la Marca y el observador no sólo son intercambiables, sino que, en la forma, son idénticos.

C. S. Peirce llegó a una idea similar en la década de 1890; véase § Trabajo relacionado.

La aritmética primaria (Capítulo 4)

La sintaxis de la aritmética primaria es la siguiente. Sólo hay dos expresiones atómicas :

• La cruz vacía  ;
• Toda o parte de la página en blanco (el “vacío”).

Hay dos reglas inductivas:

• Se puede escribir una cruz sobre cualquier expresión;
• Se pueden concatenar dos expresiones cualesquiera .

La semántica de la aritmética primaria quizás no sea nada más que la única definición explícita en LoF : "La distinción es perfecta continencia".

Sea el "estado no marcado" un sinónimo del vacío. Sea una cruz vacía el "estado marcado". Cruzar es pasar de un valor, el estado no marcado o marcado, al otro. Ahora podemos enunciar los axiomas "aritméticos" A1 y A2, que fundamentan la aritmética primaria (y, por lo tanto, todas las Leyes de la Forma):

"A1. La ley del llamado". Llamar dos veces desde un estado es indistinguible de llamar una vez. Hacer una distinción dos veces tiene el mismo efecto que hacerla una vez. Por ejemplo, decir "Hágase la luz" y luego decir "Hágase la luz" de nuevo, es lo mismo que decirlo una vez. Formalmente:

${\displaystyle \ =}$

"A2. La ley del cruce". Después de cruzar del estado no marcado al estado marcado, cruzar nuevamente ("recruzar") comenzando desde el estado marcado nos lleva al estado no marcado. Por lo tanto, volver a cruzar anula el cruce. Formalmente:

${\displaystyle \ =}$

Tanto en A1 como en A2, la expresión a la derecha de '=' tiene menos símbolos que la expresión a la izquierda de '='. Esto sugiere que cada expresión aritmética primaria puede, mediante la aplicación repetida de A1 y A2, simplificarse a uno de dos estados: el estado marcado o el estado no marcado. Este es de hecho el caso, y el resultado es la "simplificación" de la expresión. Los dos metateoremas fundamentales de la aritmética primaria establecen que:

• Toda expresión finita tiene una simplificación única. (T3 en LoF );
• Partiendo de un estado inicial marcado o no marcado, "complicar" una expresión mediante un número finito de aplicaciones repetidas de A1 y A2 no puede producir una expresión cuya simplificación difiera del estado inicial. (T4 en LoF ).

Así, la relación de equivalencia lógica divide todas las expresiones aritméticas primarias en dos clases de equivalencia : aquellas que se simplifican en cruz y aquellas que se simplifican en vacío.

A1 y A2 tienen analogías vagas en las propiedades de los circuitos eléctricos en serie y en paralelo, y en otras formas de diagramar procesos, incluidos los diagramas de flujo. A1 corresponde a una conexión en paralelo y A2 a una conexión en serie, en el entendido de que hacer una distinción corresponde a cambiar la forma en que se conectan dos puntos en un circuito, y no simplemente a agregar cableado.

La aritmética primaria es análoga a los siguientes lenguajes formales de las matemáticas y la informática :

• Una lengua Dyck con un alfabeto nulo;
• El lenguaje libre de contexto más simple en la jerarquía de Chomsky ;
• Un sistema de reescritura que es fuertemente normalizador y confluente .

La frase "cálculo de indicaciones" en LoF es un sinónimo de "aritmética primaria".

La noción de canon

Un concepto peculiar de LoF es el de "canon". Si bien LoF no define formalmente el canon, los dos siguientes extractos de las Notas del capítulo 2 son apropiados:

Las estructuras de mando más importantes se denominan a veces cánones . Son las formas en que los mandatos rectores parecen agruparse en constelaciones y, por lo tanto, no son en absoluto independientes entre sí. Un canon tiene la distinción de estar fuera (es decir, describir) el sistema en construcción, pero un mandato para construir (por ejemplo, 'trazar una distinción'), aunque pueda ser de importancia central, no es un canon. Un canon es una orden, o un conjunto de órdenes, para permitir o autorizar, pero no para construir o crear.

...la forma primaria de comunicación matemática no es la descripción sino la orden... La música es una forma de arte similar, el compositor ni siquiera intenta describir el conjunto de sonidos que tiene en mente, mucho menos el conjunto de sentimientos ocasionados por ellos, sino que escribe un conjunto de órdenes que, si son obedecidas por el intérprete, pueden resultar en una reproducción, para el oyente, de la experiencia original del compositor.

Estos extractos se refieren a la distinción en metalógica entre el lenguaje objeto, el lenguaje formal del sistema lógico en discusión, y el metalenguaje , un lenguaje (a menudo un lenguaje natural) distinto del lenguaje objeto, empleado para exponer y discutir el lenguaje objeto. La primera cita parece afirmar que los cánones son parte del metalenguaje. La segunda cita parece afirmar que las afirmaciones en el lenguaje objeto son esencialmente órdenes dirigidas al lector por el autor. Ninguna de estas afirmaciones es válida en la metalógica estándar.

El álgebra primaria (Capítulo 6)

Sintaxis

Dada cualquier expresión aritmética primaria válida, inserte en una o más posiciones cualquier número de letras latinas que tengan subíndices numéricos opcionales; el resultado es una fórmula de álgebra primaria . Las letras empleadas de esta manera en matemáticas y lógica se denominan variables . Una variable de álgebra primaria indica una posición donde se puede escribir el valor primitivo o su complemento . Múltiples instancias de la misma variable denotan múltiples posiciones del mismo valor primitivo.

Reglas que rigen la equivalencia lógica

El signo '=' puede unir dos expresiones lógicamente equivalentes; el resultado es una ecuación . Por "lógicamente equivalente" se entiende que las dos expresiones tienen la misma simplificación. La equivalencia lógica es una relación de equivalencia sobre el conjunto de fórmulas de álgebra primaria, regida por las reglas R1 y R2. Sean "C" y "D" fórmulas que contienen cada una al menos una instancia de la subfórmula A :

• R1 , Sustitución de iguales . Reemplazar una o más instancias de A en C por B , dando como resultado E . Si A = B , entonces C = E .
• R2 , Reemplazo uniforme . Reemplace todas las instancias de A en C y D con B . C se convierte en E y D se convierte en F . Si C = D , entonces E = F . Tenga en cuenta que no se requiere que A = B .

R2 se emplea con mucha frecuencia en demostraciones de álgebra primaria (ver más abajo), casi siempre de manera silenciosa. Estas reglas se invocan rutinariamente en lógica y en la mayor parte de las matemáticas, casi siempre de manera inconsciente.

El álgebra primaria consiste en ecuaciones , es decir, pares de fórmulas unidas por un operador infijo '='. R1 y R2 permiten transformar una ecuación en otra. Por lo tanto, el álgebra primaria es un sistema formal ecuacional , como las muchas estructuras algebraicas , incluida el álgebra de Boole , que son variedades . La lógica ecuacional era común antes de Principia Mathematica (por ejemplo, Peirce, ^1,2,3 Johnson 1892), y tiene defensores en la actualidad (Gries y Schneider 1993).

La lógica matemática convencional consiste en fórmulas tautológicas , señalizadas por un torniquete prefijado . Para indicar que la fórmula algebraica primaria A es una tautología , simplemente escriba " A = ". Si uno reemplaza '=' en R1 y R2 con el bicondicional , las reglas resultantes se cumplen en la lógica convencional. Sin embargo, la lógica convencional se basa principalmente en la regla modus ponens ; por lo tanto, la lógica convencional es ponencialista . La dicotomía ecuacional-ponencial destila mucho de lo que distingue a la lógica matemática del resto de las matemáticas.

Iniciales

Una inicial es una ecuación algebraica primaria verificable mediante un procedimiento de decisión y, como tal, no es un axioma . LoF establece las iniciales:

La ausencia de cualquier cosa a la derecha del "=" anterior es deliberada.

J2 es la conocida ley distributiva de la lógica sentencial y del álgebra booleana .

Otro conjunto de iniciales, más amigable para los cálculos, es:

Es gracias a C2 que el álgebra primaria es un retículo . En virtud de J1a , es un retículo complementado cuyo límite superior es . Por J0 , es el límite inferior correspondiente y el elemento identidad . J0 es también una versión algebraica de A2 y deja claro el sentido en el que se utiliza el alias con la página en blanco.

T13 en LoF generaliza C2 de la siguiente manera. Cualquier fórmula B de álgebra primaria (o lógica proposicional) puede verse como un árbol ordenado con ramas . Entonces:

T13 : Una subfórmula A se puede copiar a voluntad en cualquier profundidad de B mayor que la de A , siempre que A y su copia estén en la misma rama de B. Además, dadas múltiples instancias de A en la misma rama de B , todas las instancias excepto la más superficial son redundantes.

Aunque una prueba de T13 requeriría inducción , la intuición subyacente debería ser clara.

C2 o su equivalente se denomina:

• "Generación" en LoF ;
• "Exclusión" en Johnson (1892);
• “Pervasión” en la obra de William Bricken.

Quizás la primera instancia de un axioma o regla con el poder de C2 fue la "Regla de (De)Iteración", que combina T13 y AA=A , de los grafos existenciales de CS Peirce .

LoF afirma que la concatenación puede leerse como conmutación y asociación por defecto y, por lo tanto, no es necesario asumirla ni demostrarla explícitamente. (Peirce hizo una afirmación similar sobre sus grafos existenciales ). Sea un período una notación temporal para establecer la agrupación. Que la concatenación conmuta y asocia puede demostrarse a partir de:

• AC.D inicial = CD.A y la consecuencia AA = A (Byrne 1946). Este resultado es válido para todas las redes , porque AA = A es una consecuencia fácil de la ley de absorción , que es válida para todas las redes;
• Iniciales AC.D = AD.C y J0 . Dado que J0 se cumple solo para redes con un límite inferior, este método se cumple solo para redes acotadas (que incluyen el álgebra primaria y 2 ). La conmutatividad es trivial; solo hay que establecer A = . Asociatividad: AC.D = CA.D = CD.A = A.CD .

Demostrada la asociatividad, el punto puede descartarse.

Las iniciales en Meguire (2011) son AC.D = CD.A , llamadas B1 ; B2 , J0 arriba; B3 , J1a arriba; y B4 , C2. Por diseño, estas iniciales son muy similares a los axiomas para un grupo abeliano , G1-G3 abajo.

Teoría de la prueba

El álgebra primaria contiene tres tipos de afirmaciones demostradas:

• La consecuencia es una ecuación algebraica primaria verificada mediante una demostración . Una demostración consiste en una secuencia de pasos , cada paso justificado por una consecuencia inicial o demostrada previamente.
• Un teorema es un enunciado en el metalenguaje verificado mediante una prueba , es decir, un argumento, formulado en el metalenguaje, que es aceptado por matemáticos y lógicos entrenados.
• Inicial , definida anteriormente. Las demostraciones y pruebas invocan una inicial como si fuera un axioma.

La distinción entre consecuencia y teorema es válida para todos los sistemas formales, incluidas las matemáticas y la lógica, pero no suele hacerse explícita. Una demostración o un procedimiento de decisión se puede llevar a cabo y verificar por ordenador. La prueba de un teorema no se puede hacer.

Sean A y B fórmulas de álgebra primaria . La demostración de A = B puede realizarse de dos maneras:

• Modificar A paso a paso hasta obtener B , o viceversa;
• Simplifica ambosyA esto se le llama "cálculo".

Una vez que se ha demostrado A = B , se puede invocar A = B para justificar los pasos en demostraciones posteriores. Las demostraciones y cálculos de álgebra primaria a menudo no requieren más que J1a , J2 , C2 y las consecuencias.( C3 en LoF ),( C1 ), y AA = A ( C5 ).

La consecuencia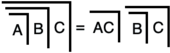, C7' en LoF , permite un algoritmo , esbozado en la prueba de LoF de T14, que transforma una fórmula de álgebra primaria arbitraria en una fórmula equivalente cuya profundidad no excede dos. El resultado es una forma normal , el análogo algebraico primario de la forma normal conjuntiva . LoF (T14–15) demuestra el análogo algebraico primario del conocido teorema del álgebra de Boole que establece que toda fórmula tiene una forma normal.

Sea A una subfórmula de alguna fórmula B . Cuando se combina con C3 , J1a puede considerarse como la condición de cierre para los cálculos: B es una tautología si y solo si A y ( A ) aparecen en la profundidad 0 de B . Una condición relacionada aparece en algunas versiones de la deducción natural . Una demostración mediante cálculo a menudo es poco más que:

• Invocar T13 repetidamente para eliminar subfórmulas redundantes;
• Borrar cualquier subfórmula que tenga la forma.

El último paso de un cálculo siempre invoca J1a .

LoF incluye nuevas y elegantes pruebas de la siguiente metateoría estándar :

• Completitud : todas las consecuencias del álgebra primaria son demostrables a partir de las iniciales (T17).
• Independencia : J1 no puede demostrarse a partir de J2 y viceversa (T18).

En todos los cursos universitarios de lógica matemática se enseña que la lógica proposicional es completa , pero en los cursos universitarios de álgebra de Boole rara vez se menciona la completitud de 2 .

Interpretaciones

Si los estados Marcado y No marcado se leen como los valores booleanos 1 y 0 (o Verdadero y Falso ), el álgebra primaria interpreta 2 (o lógica sentencial ). LoF muestra cómo el álgebra primaria puede interpretar el silogismo . Cada una de estas interpretaciones se analiza en una subsección a continuación. La extensión del álgebra primaria para que pueda interpretar la lógica estándar de primer orden aún está por hacerse, pero los gráficos existenciales beta de Peirce sugieren que esta extensión es factible.

Álgebra de Boole de dos elementos 2

El álgebra primaria es una notación minimalista elegante para el álgebra booleana de dos elementos 2 . Sea:

• Uno de los booleanos join (+) o meet (×) interpreta la concatenación ;
• El complemento de A interpreta
• 0 (1) interpreta la marca vacía si join (meet) interpreta la concatenación (porque una operación binaria aplicada a cero operandos puede considerarse como igual al elemento identidad de esa operación; o para decirlo de otra manera, un operando que falta podría considerarse como si actuara por defecto como el elemento identidad).

Si join (meet) interpreta AC , entonces meet (join) interpreta . Por lo tanto, el álgebra primaria y 2 son isomorfas, salvo por un detalle: la complementación del álgebra primaria puede ser nularia, en cuyo caso denota un valor primitivo. Módulo este detalle, 2 es un modelo del álgebra primaria. La aritmética primaria sugiere la siguiente axiomatización aritmética de 2 : 1+1=1+0=0+1=1=~0, y 0+0=0=~1. ${\displaystyle {\overline {{\overline {A|}}\ \ {\overline {C|}}{\Big |}}}}$

El conjunto es el dominio booleano o portador . En el lenguaje del álgebra universal , el álgebra primaria es la estructura algebraica de tipo . La adecuación expresiva del trazo de Sheffer apunta a que el álgebra primaria también es un álgebra de tipo . En ambos casos, las identidades son J1a, J0, C2 y ACD=CDA . Dado que el álgebra primaria y 2 son isomorfas , 2 puede verse como un álgebra de tipo . Esta descripción de 2 es más simple que la convencional, es decir, un álgebra de tipo . ${\displaystyle \ B=\{}$ ${\displaystyle ,}$ ${\displaystyle \ \}}$ ${\displaystyle \langle B,-\ -,{\overline {-\ |}},{\overline {\ \ |}}\rangle }$ ${\displaystyle \langle 2,1,0\rangle }$ ${\displaystyle \langle B,{\overline {-\ -\ |}},{\overline {\ \ |}}\rangle }$ ${\displaystyle \langle 2,0\rangle }$ ${\displaystyle \langle B,+,\lnot ,1\rangle }$ ${\displaystyle \langle 2,1,0\rangle }$ ${\displaystyle \langle B,+,\times ,\lnot ,1,0\rangle }$ ${\displaystyle \langle 2,2,1,0,0\rangle }$

Las dos interpretaciones posibles son duales entre sí en el sentido booleano. (En el álgebra de Boole, intercambiar AND ↔ OR y 1 ↔ 0 a lo largo de una ecuación produce una ecuación igualmente válida). Las identidades permanecen invariables independientemente de la interpretación elegida, por lo que las transformaciones o modos de cálculo siguen siendo los mismos; solo la interpretación de cada forma sería diferente. Ejemplo: J1a esAl interpretar la yuxtaposición como OR y como 1, esto se traduce en que es verdadero. Al interpretar la yuxtaposición como AND y como 0, esto se traduce en que también es verdadero (y el dual de ). ${\displaystyle \neg A\lor A=1}$ ${\displaystyle \neg A\land A=0}$ ${\displaystyle \neg A\lor A=1}$

dualidad operador-operando

El estado marcado, , es tanto un operador (por ejemplo, el complemento) como un operando (por ejemplo, el valor 1). Esto se puede resumir claramente definiendo dos funciones y para el estado marcado y no marcado, respectivamente: let y , donde es un conjunto (posiblemente vacío) de valores booleanos. ${\displaystyle m(x)}$ ${\displaystyle u(x)}$ ${\displaystyle m(x)=1-\max(\{0\}\cup x)}$ ${\displaystyle u(x)=\max(\{0\}\cup x)}$ ${\displaystyle x}$

Esto revela que es el valor 0 o el operador OR, mientras que es el valor 1 o el operador NOR, dependiendo de si es el conjunto vacío o no. Como se señaló anteriormente, existe una forma dual de estas funciones que intercambian AND ↔ OR y 1 ↔ 0. ${\displaystyle u}$ ${\displaystyle m}$ ${\displaystyle x}$

Lógica oracional

Sea la página en blanco la que denota Falso y sea una Cruz la que se lee No. Entonces la aritmética primaria tiene la siguiente lectura oracional:

 =   Falso

 =   Verdadero  =   no Falso

 =   No es cierto  =   Falso

El álgebra primaria interpreta la lógica proposicional de la siguiente manera: una letra representa cualquier expresión propositiva dada. Por lo tanto:

interpreta No A

interpreta A o B

interpreta No A o B o Si A entonces B.

interpreta No (No A o No B)

o no (si A entonces no B)

o A y B.

Por lo tanto, cualquier expresión en lógica proposicional tiene una traducción algebraica primaria . De manera equivalente, el álgebra primaria interpreta la lógica proposicional. Dada una asignación de cada variable a los estados Marcado o No marcado, esta traducción algebraica primaria se reduce a una expresión aritmética primaria, que puede simplificarse. Al repetir este ejercicio para todas las asignaciones posibles de los dos valores primitivos a cada variable, se revela si la expresión original es tautológica o satisfacible . Este es un ejemplo de un procedimiento de decisión , uno más o menos en el espíritu de las tablas de verdad convencionales. Dada una fórmula algebraica primaria que contiene N variables, este procedimiento de decisión requiere simplificar 2 ^N fórmulas aritméticas primarias. Para un procedimiento de decisión menos tedioso más en el espíritu del "análisis del valor de verdad" de Quine , véase Meguire (2003).

Schwartz (1981) demostró que el álgebra primaria es equivalente —sintácticamente , semánticamente y en términos de demostración teórica— al cálculo proposicional clásico . Asimismo, se puede demostrar que el álgebra primaria es sintácticamente equivalente a expresiones construidas de la manera habitual a partir de los valores de verdad clásicos true y false , los conectores lógicos NOT, OR y AND, y los paréntesis.

Interpretar el estado no marcado como falso es completamente arbitrario; ese estado también puede leerse como verdadero . Todo lo que se requiere es que la interpretación de la concatenación cambie de OR a AND. IF A THEN B ahora se traduce comoen lugar deEn términos más generales, el álgebra primaria es "autodual " , lo que significa que cualquier fórmula del álgebra primaria tiene dos lecturas oracionales o booleanas , cada una dual de la otra. Otra consecuencia de la autodualidad es la irrelevancia de las leyes de De Morgan ; esas leyes están incorporadas a la sintaxis del álgebra primaria desde el principio.

Ahora surge la verdadera naturaleza de la distinción entre el álgebra primaria por un lado, y la lógica 2 y la lógica propositiva por el otro. En estos últimos formalismos, la complementación / negación que opera sobre la "nada" no está bien formada. Pero una cruz vacía es una expresión de álgebra primaria bien formada , que denota el estado marcado, un valor primitivo. Por lo tanto, una cruz no vacía es un operador , mientras que una cruz vacía es un operando porque denota un valor primitivo. Así, el álgebra primaria revela que los conceptos matemáticos hasta ahora distintos de operador y operando son, de hecho, meramente facetas diferentes de una única acción fundamental, la realización de una distinción.

Silogismos

El Apéndice 2 de LoF muestra cómo traducir silogismos tradicionales y sorites al álgebra primaria . Un silogismo válido es simplemente uno cuya traducción al álgebra primaria se simplifica a una Cruz vacía. Sea A * un literal , es decir, A o , indistintamente. Entonces cada silogismo que no requiere que uno o más términos se supongan no vacíos es una de las 24 permutaciones posibles de una generalización de Barbara cuyo equivalente al álgebra primaria es . Estas 24 permutaciones posibles incluyen las 19 formas silogísticas consideradas válidas en la lógica aristotélica y medieval . Esta traducción al álgebra primaria de la lógica silogística también sugiere que el álgebra primaria puede interpretar la lógica monádica y de términos , y que el álgebra primaria tiene afinidades con los esquemas de términos booleanos de Quine (1982: Parte II). ${\displaystyle {\overline {A|}}}$ ${\displaystyle {\overline {A^{*}\ B|}}\ \ {\overline {{\overline {B|}}\ C^{*}{\Big |}}}\ A^{*}\ C^{*}}$

Un ejemplo de cálculo

El siguiente cálculo del teorema Praeclarum no trivial de Leibniz ejemplifica el poder demostrativo del álgebra primaria . Sea C1 = A , C2 , C3 , J1a , y sea OI lo que significa que las variables y subfórmulas se han reordenado de una manera que lo permiten la conmutatividad y la asociatividad. ${\displaystyle {\overline {{\overline {A|}}{\Big |}}}}$ ${\displaystyle A\ {\overline {A\ B|}}=A\ {\overline {B|}}}$ ${\displaystyle {\overline {\ \ |}}\ A={\overline {\ \ |}}}$ ${\displaystyle {\overline {A|}}\ A={\overline {\ \ |}}}$

Relación con los magmas

El álgebra primaria incorpora un punto señalado por Huntington en 1933: el álgebra de Boole requiere, además de una operación unaria , una, y no dos, operaciones binarias . De ahí el hecho, rara vez observado, de que las álgebras de Boole son magmas . (Los magmas se llamaban grupoides hasta que la teoría de categorías se apropió de este último término ). Para ver esto, observe que el álgebra primaria es conmutativa :

• Semigrupo porque la yuxtaposición del álgebra primaria conmuta y asocia ;
• Monoide con elemento identidad , en virtud de J0 .

Los grupos también requieren una operación unaria , llamada inversa , la contraparte grupal de la complementación booleana . Seadenota la inversa de a . Sea denotado el elemento identidad del grupo . Entonces los grupos y el álgebra primaria tienen las mismas firmas , es decir, ambos son álgebras de tipo 〈2,1,0〉. Por lo tanto, el álgebra primaria es un álgebra de contorno . Los axiomas para un grupo abeliano , en notación de contorno, son: ${\displaystyle \langle -\ -,{\overline {-\ |}},{\overline {\ \ |}}\rangle }$

• G1 . abc = acb (asumiendo asociación desde la izquierda);
• G2 .
• G3 ..

A partir de G1 y G2 , se puede derivar la conmutatividad y asociatividad de la concatenación, como se indicó anteriormente. Nótese que G3 y J1a son idénticos. G2 y J0 serían idénticos si    =    reemplazó a A2 . Esta es la identidad aritmética definitoria de la teoría de grupos, en notación de límites.

El álgebra primaria se diferencia de un grupo abeliano en dos aspectos:

• De A2 , se sigue que ≠ . Si el álgebra primaria fuera un grupo , = se cumpliría, y uno de    a  =     o    a   =  a    tendría que ser una consecuencia primaria del álgebra . Nótese queyson complementos mutuos del álgebra primaria , como lo requiere la teoría de grupos, por lo que esto es cierto tanto para la teoría de grupos como para el álgebra primaria ; ${\displaystyle {\overline {\ {\overline {\ {\overline {\ \ |}}\ {\Big |}}}\ {\Bigg |}}}={\overline {\ \ |}}}$
• C2 delimita más claramente el álgebra primaria de otros magmas, porque C2 permite demostrar la ley de absorción que define las redes y la ley distributiva central del álgebra de Boole .

Tanto A2 como C2 se deducen de que B es un conjunto ordenado .

Ecuaciones de segundo grado (Capítulo 11)

El capítulo 11 de LoF presenta ecuaciones de segundo grado , compuestas por fórmulas recursivas que pueden considerarse de profundidad "infinita". Algunas fórmulas recursivas se simplifican al estado marcado o no marcado. Otras "oscilan" indefinidamente entre los dos estados dependiendo de si una profundidad dada es par o impar. Específicamente, ciertas fórmulas recursivas pueden interpretarse como oscilantes entre verdadero y falso a lo largo de intervalos sucesivos de tiempo, en cuyo caso se considera que una fórmula tiene un valor de verdad "imaginario". De esta manera, el flujo del tiempo puede introducirse en el álgebra primaria .

Turney (1986) muestra cómo estas fórmulas recursivas pueden interpretarse a través de la Aritmética Recursiva Restringida (ARR) de Alonzo Church . Church introdujo la ARR en 1955 como una formalización axiomática de los autómatas finitos . Turney (1986) presenta un método general para traducir ecuaciones de segundo grado a la ARR de Church, ilustrando su método utilizando las fórmulas E1 , E2 y E4 en el capítulo 11 de LoF . Esta traducción a la ARR arroja luz sobre los nombres que Spencer-Brown dio a E1 y E4 , a saber, "memoria" y "contador". La ARR formaliza y aclara así la noción de LoF de un valor de verdad imaginario.

Trabajo relacionado

Gottfried Leibniz , en memorandos no publicados antes de finales del siglo XIX y principios del XX, inventó la lógica booleana . Su notación era isomorfa a la de LoF : la concatenación se lee como conjunción y "no-( X )" se lee como el complemento de X . El reconocimiento del papel pionero de Leibniz en la lógica algebraica fue presagiado por Lewis (1918) y Rescher (1954). Pero una apreciación completa de los logros de Leibniz tuvo que esperar al trabajo de Wolfgang Lenzen, publicado en la década de 1980 y reseñado en Lenzen (2004).

Charles Sanders Peirce (1839-1914) anticipó el álgebra primaria en tres líneas de trabajo:

1. En dos artículos que escribió en 1886 proponían un álgebra lógica que empleaba un solo símbolo, el streamer , casi idéntico a la cruz de LoF . La semántica del streamer es idéntica a la de la cruz, excepto que Peirce nunca escribió un streamer sin nada debajo. Un extracto de uno de estos artículos se publicó en 1976, ^[9] pero no se publicaron en su totalidad hasta 1993. ^[10]
2. En un artículo de enciclopedia de 1902, ^[11] Peirce anotó el álgebra de Boole y la lógica oracional de la misma manera que esta entrada, excepto que empleó dos estilos de corchetes, alternando entre '(', ')' y '[', ']' con cada incremento en la profundidad de la fórmula.
3. La sintaxis de sus gráficos existenciales alfa es meramente concatenación , leída como conjunción , y encerramiento por óvalos, leído como negación . ^[12] Si la concatenación del álgebra primaria se lee como conjunción , entonces estos gráficos son isomorfos al álgebra primaria (Kauffman 2001).

Irónicamente, LoF cita el vol. 4 de los Collected Papers de Peirce , la fuente de los formalismos en (2) y (3) arriba. (1)-(3) eran virtualmente desconocidos en el momento en que (1960) y en el lugar donde (Reino Unido) se escribió LoF . La semiótica de Peirce , sobre la cual LoF no dice nada, puede aún arrojar luz sobre los aspectos filosóficos de LoF .

Kauffman (2001) analiza otra notación similar a la de LoF , la de un artículo de 1917 de Jean Nicod , quien fue discípulo de Bertrand Russell .

Los formalismos anteriores son, como el álgebra primaria , todos los casos de matemáticas de frontera , es decir, matemáticas cuya sintaxis se limita a letras y corchetes (dispositivos de encierro). Una sintaxis minimalista de esta naturaleza es una "notación de frontera". La notación de frontera está libre de operadores infijos, prefijos o símbolos de operadores posfijos . Las muy conocidas llaves ('{', '}') de la teoría de conjuntos pueden verse como una notación de frontera.

El trabajo de Leibniz, Peirce y Nicod es inocente de metateoría, ya que escribieron antes del artículo fundamental de Emil Post de 1920 (que LoF cita), que demostraba que la lógica oracional es completa, y antes de que Hilbert y Łukasiewicz mostraran cómo demostrar la independencia de los axiomas usando modelos .

Craig (1979) sostuvo que el mundo, y la forma en que los humanos lo perciben e interactúan con él, tiene una rica estructura booleana. Craig era un lógico ortodoxo y una autoridad en lógica algebraica .

La ciencia cognitiva de segunda generación surgió en la década de 1970, después de que se escribiera LoF . Sobre la ciencia cognitiva y su relevancia para el álgebra de Boole, la lógica y la teoría de conjuntos , véase Lakoff (1987) (ver las entradas del índice bajo "Ejemplos de esquemas de imagen: contenedor") y Lakoff y Núñez (2001). Ninguno de los dos libros cita LoF .

Los biólogos y científicos cognitivos Humberto Maturana y su alumno Francisco Varela hablan de la LoF en sus escritos, en los que identifican la "distinción" como el acto cognitivo fundamental. La psicóloga y científica cognitiva de Berkeley Eleanor Rosch ha escrito extensamente sobre la noción estrechamente relacionada de categorización.

Otros sistemas formales con posibles afinidades con el álgebra primaria incluyen:

• La mereología, que por lo general tiene una estructura reticular muy similar a la del álgebra de Boole, para algunos autores la mereología es simplemente un modelo del álgebra de Boole y, por lo tanto, también del álgebra primaria.
• Mereotopología , que es inherentemente más rica que el álgebra de Boole;
• El sistema de Whitehead (1934), cuyo primitivo fundamental es la “indicación”.

La aritmética y el álgebra primarias son un formalismo minimalista para la lógica de oraciones y el álgebra de Boole. Otros formalismos minimalistas que tienen el poder de la teoría de conjuntos incluyen:

• El cálculo lambda ;
• Lógica combinatoria con dos ( S y K ) o incluso uno ( X ) combinadores primitivos;
• La lógica matemática se basa en tres conceptos primitivos: un conectivo, NAND (cuya traducción algebraica primaria es o, dualmente, ), cuantificación universal y una fórmula atómica binaria , que denota la pertenencia a un conjunto . Este es el sistema de Quine (1951). ${\displaystyle {\overline {A\ \ B\ |}}}$ ${\displaystyle {\overline {A|}}\ \ {\overline {B|}}}$
• Los grafos existenciales beta , con un único predicado binario que denota la pertenencia a un conjunto. Esto aún está por explorar. Los grafos alfa mencionados anteriormente son un caso especial de los grafos beta .

Ediciones

• 1969. Londres: Allen & Unwin, tapa dura.
• 1972. Crown Publishers, tapa dura: ISBN  0-517-52776-6
• 1973. Bantam Books, edición de bolsillo. ISBN 0-553-07782-1 
• 1979. EP Dutton, libro de bolsillo. ISBN 0-525-47544-3 
• 1994. Portland, OR: Cognizer Company, libro de bolsillo. ISBN 0-9639899-0-1 
• Traducción al alemán de 1997, titulada Gesetze der Form . Lübeck: Bohmeier Verlag. ISBN 3-89094-321-7 
• 2008 Bohmeier Verlag, Leipzig, 5ª edición internacional. ISBN 978-3-89094-580-4 

Véase también

• Álgebra de Boole  – Manipulación algebraica de “verdadero” y “falso”
• Álgebras de Boole definidas canónicamente  : un tratamiento técnico de las álgebras de Boole
• Gráfico entitativo  : tipo de notación diagramática para lógica proposicionalPages displaying short descriptions of redirect targets
• Grafo existencial  : tipo de notación diagramática para lógica proposicional
• Marca y espacio  – Estados de una señal de comunicaciones
• Programación y metaprogramación  : libro de no ficción de 1968 de John C. Lilly
• Cálculo proposicional  – Rama de la lógica
• Álgebra de Boole de dos elementos  – Álgebra de Boole
• Lista de temas de álgebra de Boole

Notas

1. Meguire, P. (2011) Álgebra de límites: un enfoque más simple para la lógica básica y el álgebra de Boole. Saarbrücken: VDM Publishing Ltd. 168pp
2. Schönwälder-Kuntze, Tatjana; Wille, Katrin; Hölscher, Thomas; Spencer Brown, George (2009). "George Spencer Brown: Eine Einführung in die Laws of Form , 2. Auflage" . Wiesbaden: VS Verlag für Sozialwissenschaften. ISBN 978-3-531-16105-1.
3. Felix Lau: Die Form der Paradoxie , 2005 Carl-Auer Verlag, ISBN 9783896703521 
4. George Spencer-Brown. Leyes de la forma. 1969, Pub. George Allen y Unwin. SBN 04 510028 4
5. Müller, Albert (2008). "Computación de una realidad. Conferencia de Heinz von Foerster en la Conferencia AUM en 1973" (PDF) . Fundamentos constructivistas . 4 (1): 62–69.
6. Beer, Stafford (1969). "Matemáticas creadas". Nature . 223 (5213): 1392–1393. Código Bibliográfico :1969Natur.223.1392B. doi :10.1038/2231392b0. S2CID  5223774.
7. B. Banaschewski (julio de 1977). "Sobre las leyes de la forma de G. Spencer Brown". Notre Dame Journal of Formal Logic . 18 (3): 507–509. doi : 10.1305/ndjfl/1093888028 .
8. Para una evaluación comprensiva, véase Kauffman (2001).
9. "Qualitative Logic", MS 736 (c. 1886) en Eisele, Carolyn, ed. 1976. Los nuevos elementos de las matemáticas por Charles S. Peirce . Vol. 4, Filosofía matemática . (La Haya) Mouton: 101-15.1
10. "Qualitative Logic", MS 582 (1886) en Kloesel, Christian et al., eds., 1993. Writings of Charles S. Peirce: A Chronological Edition , Vol. 5, 1884–1886 . Indiana University Press : 323-71. "The Logic of Relatives: Qualitative and Quantitative", MS 584 (1886) en Kloesel, Christian et al., eds., 1993. Writings of Charles S. Peirce: A Chronological Edition, Vol. 5, 1884–1886 . Indiana University Press: 372-78.
11. Reimpreso en Peirce, CS (1933) Collected Papers of Charles Sanders Peirce , vol. 4 , Charles Hartshorne y Paul Weiss , eds. Harvard University Press . Párrafos 378–383.
12. Los gráficos existenciales se describen en detalle en Peirce, CS (1933) Collected Papers, Vol. 4 , Charles Hartshorne y Paul Weiss , eds. Harvard University Press. Párrafos 347–529.

Bibliografía

• Bostock, David, 1997. Lógica intermedia . Oxford Univ. Press.
• Byrne, Lee, 1946, "Dos formulaciones del álgebra de Boole", Boletín de la Sociedad Matemática Americana : 268–71.
• Craig, William (1979). "Lógica booleana y el mundo físico cotidiano". Actas y discursos de la Asociación Filosófica Americana . 52 (6): 751–78. doi :10.2307/3131383. JSTOR  3131383.
• David Gries y Schneider, FB, 1993. Un enfoque lógico para las matemáticas discretas . Springer-Verlag.
• William Ernest Johnson , 1892, "El cálculo lógico", Mente 1 (ns): 3–30.
• Louis H. Kauffman, 2001, "Las matemáticas de CS Peirce", Cibernética y conocimiento humano 8: 79–110.
• ------, 2006, "Reformulación del teorema del color del mapa".
• ------, 2006a. “Leyes de la forma: una exploración de las matemáticas y sus fundamentos”. Borrador de libro (de ahí su gran tamaño).
• Lenzen, Wolfgang, 2004, "La lógica de Leibniz" en Gabbay, D., y Woods, J., eds., El surgimiento de la lógica moderna: de Leibniz a Frege (Manual de la historia de la lógica – Vol. 3) . Ámsterdam: Elsevier, 1–83.
• Lakoff, George , 1987. Mujeres, fuego y cosas peligrosas . University of Chicago Press.
• -------- y Rafael E. Núñez , 2001. De dónde vienen las matemáticas : cómo la mente encarnada trae las matemáticas a la existencia . Libros básicos.
• Meguire, PG (2003). "Descubrimiento del álgebra de límites: una notación simplificada para el álgebra de Boole y los funtores de verdad". Revista internacional de sistemas generales . 32 : 25–87. CiteSeerX  10.1.1.106.634 . doi :10.1080/0308107031000075690. S2CID  9460101.
• --------, 2011. Álgebra de límites: un enfoque más simple de la lógica básica y el álgebra de Boole . VDM Publishing Ltd. ISBN 978-3639367492 . Fuente de gran parte de esta entrada, incluida la notación que encierra entre paréntesis lo que LoF coloca bajo una cruz. Evita los aspectos más especulativos de LoF . 
• Willard Quine , 1951. Lógica matemática , 2.ª ed. Harvard University Press.
• --------, 1982. Métodos de lógica , 4ª ed. Harvard University Press.
• Rescher, Nicholas (1954). "La interpretación de Leibniz de sus cálculos lógicos". Revista de lógica simbólica . 18 (1): 1–13. doi :10.2307/2267644. JSTOR  2267644. S2CID  689315.
• Schwartz, Daniel G. (1981). "Isomorfismos de las leyes de la forma de G. Spencer-Brown y el cálculo de autorreferencia de F. Varela". Revista Internacional de Sistemas Generales . 6 (4): 239–55. doi :10.1080/03081078108934802.
• Turney, PD (1986). " Leyes de la forma y autómatas finitos". Revista Internacional de Sistemas Generales . 12 (4): 307–18. doi :10.1080/03081078608934939.
• AN Whitehead , 1934, "Indicación, clases, número, validación", Mind 43 (ns): 281–97, 543. Las correcciones en la pág. 543 son numerosas e importantes, y las reimpresiones posteriores de este artículo no las incorporan.
• Dirk Baecker (ed.) (1993), Kalkül der Form. Suhrkamp; Dirk Baecker (ed.), Probleme der Form . Suhrkamp.
• Dirk Baecker (ed.) (1999), Problemas de forma , Stanford University Press.
• Dirk Baecker (ed.) (2013), Una matemática de la forma, una sociología de los observadores , Cibernética y conocimiento humano, vol. 20, no. 3-4.
• Louis H. Kauffman (ed.) (2019), Cybernetics & Human Knowing, vol. 26, no. 2-3. Número especial, Leyes de la forma: Spencer-Brown en Esalen, 1973 .

Enlaces externos

• Leyes de la forma, archivo del sitio web de Richard Shoup.
• Charlas de Spencer-Brown en Esalen, 1973. Las formas autorreferenciales se introducen en la sección titulada "Grado de ecuaciones y teoría de tipos".
• Grabación de audio de la sesión inaugural de la Conferencia AUM de 1973 en Esalen.
• Louis H. Kauffman, "Álgebra de cajas, matemáticas de límites, lógica y leyes de la forma".
• Kissel, Matthias, "Una introducción no sistemática pero fácil de entender a las Leyes de la Forma".
• Foro de Leyes de la Forma, donde se discute el álgebra primaria y los formalismos relacionados desde 2002.
• Un encuentro con GSB por Moshe Klein
• La Marca Marcable, una introducción por etapas sencillas a las ideas de las Leyes de la Forma
• El cálculo BF y la raíz cuadrada de la negación de Louis Kauffman y Arthur Collings; amplía las leyes de la forma añadiendo un valor lógico imaginario. (Los valores lógicos imaginarios se introducen en el capítulo 11 del libro Leyes de la forma ).
• Curso Leyes de la Forma: un curso gratuito en línea que guía a las personas a través del cuerpo principal del texto de Leyes de la Forma de Leon Conrad, el último estudiante de Spencer-Brown, quien estudió la obra con el autor.